Реферат - Матричные игры
Подождите немного. Документ загружается.


11
h=
a
22
−a
12
a
11
−a
12
−a
21
+a
22
.
4.2. m
×
n – игры
В некоторых случаях игры больших размеров можно упростить и
привести к малым размерам. В основе такого преобразования лежит понятие
доминирования стратегий.
Пусть дана m
×
n - игра А. Говорят, что i-я стратегия игрока A
доминирует его k-ю стратегия, если
a
ij
≥ a
kj
для всех j = 1,2,…,n. Говорят, что j-я
стратегия игрока B доминирует его l-и стратегию, если
a
ij
≤ a
kl
для всех i = 1,2,
…,m. .
FFFFFFFFИз определения видно, что доминирующая стратегия дает игроку выигрыш
не хуже, чем доминируемая. Отсюда следует, что игрок всегда может обойтись
без доминируемых стратегий, в частности, если есть одинаковые стратегии, то
он может применять только одну из них. Поэтому в матрице А доминируемые
стратегии (строки или столбцы) могут быть отброшены, а это приводит к
матрице малых размеров. В результате выполнения доминирования получается
игра, эквивалентная первоначальной, в смысле следующего утверждения.
Теорема 2. Пусть (x,y) - седловая точка m
×
n - игры А, а (
x
'
, y
'
) - седловая
точка
m
'
× n
'
- игры A' (
m
'
<m , n
'
<n
), полученной из А в результате исключения
доминируемых стратегий. Тогда
x
i
'
=x
i
,
y
i
'
= y
i
для всех недоминируемых i, j:
x
i
=0,
y
i
=0
для всех доминируемых i:
V
(
A
'
)
=V (A )
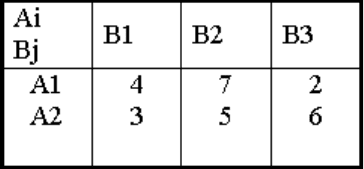
Пример 1. Рассмотрим игру
12
Стрелками показаны доминируемые стратегии. Получили 2х2-игру, в
которой все стратегии недоминируемы. Игра
A
'
эквивалентна первоначальной
игре А, т.е. оптимальные стратегии в игре А имеют вид x=(0,
x
2
, x
3
),
y=( y
1
, y
2
, 0 , 0)
FFFFFFFFВ результате вместо игры А мы можем решить более простую 2х2-
игру
A
'
.
Теперь мы можем указать общий порядок решения матричной игры:
1. проверить, существует ли решение в чистых стратегиях; если есть,
то игра решена;
2. если нет решения в чистых стратегиях, то выполнить
доминирование;
3. найти решение в смешанных стратегиях.
13
4.3. Решение игр 2
× nи m ×2
Для построения решений 2
× nи m ×2
- игр существует эффективный метод,
основанный на простых геометрических соображениях. Этот метод называют
графическим.
Рассмотрим игру 2
¿
n:
А=¿
(
а
11
а
12
.. . а
1 n
¿
)
¿
¿
¿¿
.
Задача игрока A состоит в максимизации функции
g(u )=min
j
(a
1 j
u
1
+a
2 j
u
2
)
.Так как
u
1
=1−u
2
, мы имеем
g(u
2
)=min
j
{(a
2 j
−a
1 j
)u
2
+a
1 j
}
.
Таким образом, v является минимумом n линейных функций одной
переменной
u
2
; можно вычертить графики этих функций и затем
максимизировать их минимум g(
u
2
) графическими методами. Покажем на
примере игры 2
¿
3.
Поясним на примере 1.
На плоскости хОу введём систему координат и на оси Ох отложим
отрезок единичной длины А1, А2, каждой точке которого поставим в
соответствие некоторую смешанную стратегию игрока 1 (х, 1-х). В частности,
точке А1 (0;0) отвечает стратегия А1, точке А2 (1;0) - стратегии А2 и т. д.
А=¿
(
а
11
а
12
...а
1n
¿
)
¿
¿
¿¿
g(u)=min
j
(a
1j
u
1
+a
2j
u
2
)
g(u
2
)=min
j
{(a
2j
−a
1j
)u
2
+a
1j
}
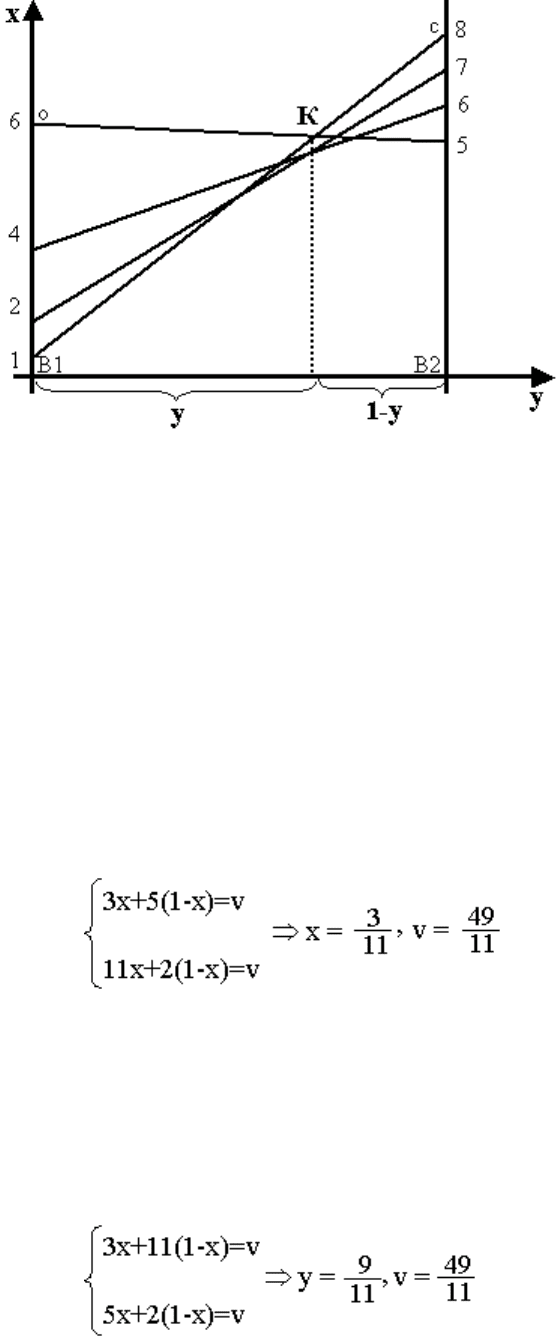
14
На перпендикуляре А1 будем откладывать выигрыш игрока 1 при
стратегии 1, на втором - при стратегии А2.
Таким образом, ординаты точек, принадлежащих ломаной оMNс
определяют минимальный выигрыш игрока 1 при применении им любой
смешанной стратегии. Эта минимальная величина является максимальной в
точке N; следовательно, этой точке соответствует оптимальная стратегия Х* =
(х, 1-х), а её ордината равна цене игры. Координаты точки N находим как
пересечение прямых.
Соответствующие два уравнения имеют вид
следовательно, х = (3/11,9/11), при цене игры v = 49/11. таким образом мы
можем найти оптимальную стратегию при помощи матрицы
(
3 11
4 2
)
Оптимальные стратегии для игрока 2 можно найти из системы
Укажем основные этапы нахождения решения игры 2
¿
n (m
¿
2):
15
1)FFСтроим прямые, соответствующие стратегиям второго (первого)
игрока.
2)FFОпределяем нижнюю (верхнюю) огибающую графиков,
соответствующих столбцам (строкам).
3)FFНаходим две стратегии второго (первого) игрока, которым
соответствует две прямые, пересекающиеся в точке с максимальной
(минимальной) ординатой.
4)FFОпределяем цену игры и оптимальные стратегии игроков.

16
4.4. Решение игр симплекс-методом
FFСимплекс-метод является самым распространенным и наиболее
универсальным методом решения задач линейного программирования (ЗЛП).
Любую матричную игру можно свести к ЗЛП, точнее, задачам нахождения
оптимальных стратегий первого и второго игроков в каждой матричной игре
соответствует пара двойственных ЗЛП. Благодаря этому становится
возможным применение симплекс-метода для решения матричной игры.
FFFFFFFFПусть игрок A играет оптимально, а игрок B вместо
y
¿
выбирает чистую
стратегию j. По определению седловой точки, каждому такому отклонению
соответствует неравенство:
При j=1
a
11
x
1
¿
+…+a
m1
x
m
¿
≥V
При j=2
a
12
x
1
¿
+…+a
m 2
x
m
¿
≥ V
При j=n
a
1n
x
1
¿
+…+a
mn
x
m
¿
≥ V
FFFFПредположим, что V>0. Разделим обе части каждого неравенства на V
и введем новую переменную
ε
i
=x
i
¿
/V
. Тогда мы имеем:
a
11
ε
i
+…+a
m1
ε
m
≥ 1
a
12
ε
i
+…+a
m2
ε
m
≥1
a
1n
ε
i
+…+a
mn
ε
m
≥ 1
Рассмотрим сумму
Z=
ε
1
+…+ε
m
=
x
1
¿
V
+...+x
m
¿
/V
=1/V.
FЦелью игрока A является получение максимального выигрыша. Легко
видеть, что это равносильно уменьшению функции Z. Пользуясь новыми
переменными
ε
i
, задачу вычисления оптимальной стратегии
x
¿
игрока A можем
теперь сформулировать так:
Найти
ε
1
, … ,ε
m
такие что Z=
∑
i
ε
i
→ min ,
при ограничениях
∑
i
a
ij
ε
i
≥ 1
, i = 1,2,
…,m, j = 1,2,…,n,
ε
i
≥ 0
. Здесь
ε=x
i
¿
/V
, Z=1/V.
17
Рассуждая аналогично, задачу нахождения оптимальной стратегии
игрока B можно написать следующим образом:
Найти
❑
1
, … ,❑
m
такие что W=
∑
J
❑
j
→max ,
при ограничениях
∑
j
a
ij
❑
j
≤ 1
, i =
1,2,…,m, j = 1,2,…,n,
❑
j
≥ 0
. Здесь
¿ y
j
¿
/V
, W=1/V.
FЗадачи представляют собой пару двойственных задач линейного
программирования. Суть применения симплекс-метода такова: решая задачу,
находим ее оптимальный план и значение
Z
¿
,W
¿
, V,
x
¿
, y
¿
.
18
Заключение
Матричные игры широко используются в системах принятия решений.
Они могут служить математическими моделями многих простейших
конфликтных ситуаций из области экономики, математической статистики,
военного дела, биологии. Нередко в качестве одного из игроков рассматривают
«природу», под которой понимается вся совокупность внешних обстоятельств,
неизвестных принимающему решения лицу (другому игроку).
19
Список литературы
1. Шишкин Е.В., Чхартишвили А.Г. Математические методы и
модели в управлении: Учеб. Пособие. – М.: Дело, 2000.
2. Лапшин К.А. Методические указания для студентов
экономического факультета «Игровые модели и принятие решений». – М. 2001.
3. http://www.math.kemsu.ru
http://www.sosh.ru
