Реферат - Комплексные числа и их свойства
Подождите немного. Документ загружается.


Ясно что .
Итак,
Пример. Выразить через и через .
Решение. Запишем формулу Муавра при :
.
Левую часть раскроем по формуле куба суммы:
Итак,
Используя условия равенства комплексных чисел, получаем:
1)
Итак,
Пример. Найти сумму
Решение. Для комплексного числа рассмотрим
геометрическую прогрессию 1, z, z
2
, z
3
, …со знаменателем z.Запишем формулу
для суммы первых членов этой прогрессии:
.
К каждому слагаемому левой части применим формулу Муавра:
Осталось найти действительную и мнимую части дроби ,
А затем воспользоваться тем, что действительная часть равна С, а мнимая часть
равна S.Отсюда и получается нужные формулы для С и S. Сначала преобразуем
знаменатель:
21

Значит,
В итоге получаем:
10.Перевод z =a+bi из тригонометрической формы в алгебраическую.
z = r (cosφ + i sinφ)
1. Раскроем скобки: z = r
.
cosφ + i
.
r
.
sinφ
2. z = a + bi. Перевод очевиден
Пример. z = 5 (cos120
0
+ i
.
sin120
0
)
Решение. z = 5 (-1/2) + i
.
5
.
(
3
/2);
z = -5/2 +5
3
/2
.
i
Геометрически сумма комплексных чисел равна суммарному вектору,
слагаемыми которого служат векторы суммируемых комплексных чисел.
(Сложение векторов производятся по правилам, изложенным в геометрии.)
Разность векторов комплексных чисел тоже равна вектору разности.
11.Перемножение комплексных чисел в тригонометрической форме.
В этом разделе используются следующие тригонометрические формулы:
sin (α + β) = sin α
.
cos β + cos α
.
sin β;
sin (α - β) = sin α
.
cos β - cos α
.
sin β;
cos (α + β) = cos α
.
cos β - sin α
.
sin β;
cos (α - β) = cos α
.
cos β + sin α
.
sin β.
22

Запишем два комплексных числа в тригонометрической форме:
z
1
= r
1
(cosφ
1
+ i
.
sinφ
1
) и z
2
= r
2
(cosφ
2
+ i
.
sinφ
2
)
Вычислим их произведение в тригонометрической форме по правилам
перемножения комплексных чисел:
z
1
.
z
2
= r
1
(cosφ
1
+ i
.
sinφ
1
)
.
r
2
(cosφ
2
+ i
.
sinφ
2
) = r
1
.
r
2
(cosφ
1
+ i
.
sinφ
1
) (cosφ
2
+ i
.
sinφ
2
) =
=r
1
.
r
2
(cosφ
1
.
cosφ
2
+ i
.
cosφ
1
.
sinφ
2
+ i
.
sinφ
1
.
cosφ
2
+ i
2.
sinφ
1
.
sinφ
2
) = r
1
.
r
2
((cosφ
1
.
cosφ
2
-
sinφ
1
.
sinφ
2
) + i(sinφ
1
.
cosφ
2
+ sinφ
2
.
cosφ
1
)) = r
1
.
r
2
[cos(φ
1
+ φ
2
) + i
.
sin(φ
1
+ φ
2
)]
Применяя это правило, получаем формулу для возведения комплексного числа
в любую степень: [r(cosφ + i
.
sinφ)]
n
= r
n
(cos
.
n
.
φ + i
.
sin
.
n
.
φ)
12. Возведение комплексного числа в степень.
Формула Муавра.
(ρ(cosα+i sinα))
n
= ρ
n
(cos nα+i sin nα), n
N
Пример: (cos 15°+i sin 15°)
6
=cos(15°·6)+i sin (15°·6)=cos 90°+i sin 90°=i
Следствие 1. (ρ(cosα+i sinα))
n
=ρ
n
(cos na+i sin na),n
Z
Следствие 2.(cos α+i sin α)
n
=cos na+i sin na,n
Z
Следствие 3. Если модуль комплексного числа z равен единице, а его аргумент
равен 2π/m (m=3,4,5…), то множество степеней z
0
,z
1
,z
2
,z
3
,…z
m-1
образует на
комплексной плоскости множество вершин правильного m-угольника,
вписанного в единичную окружность.
23
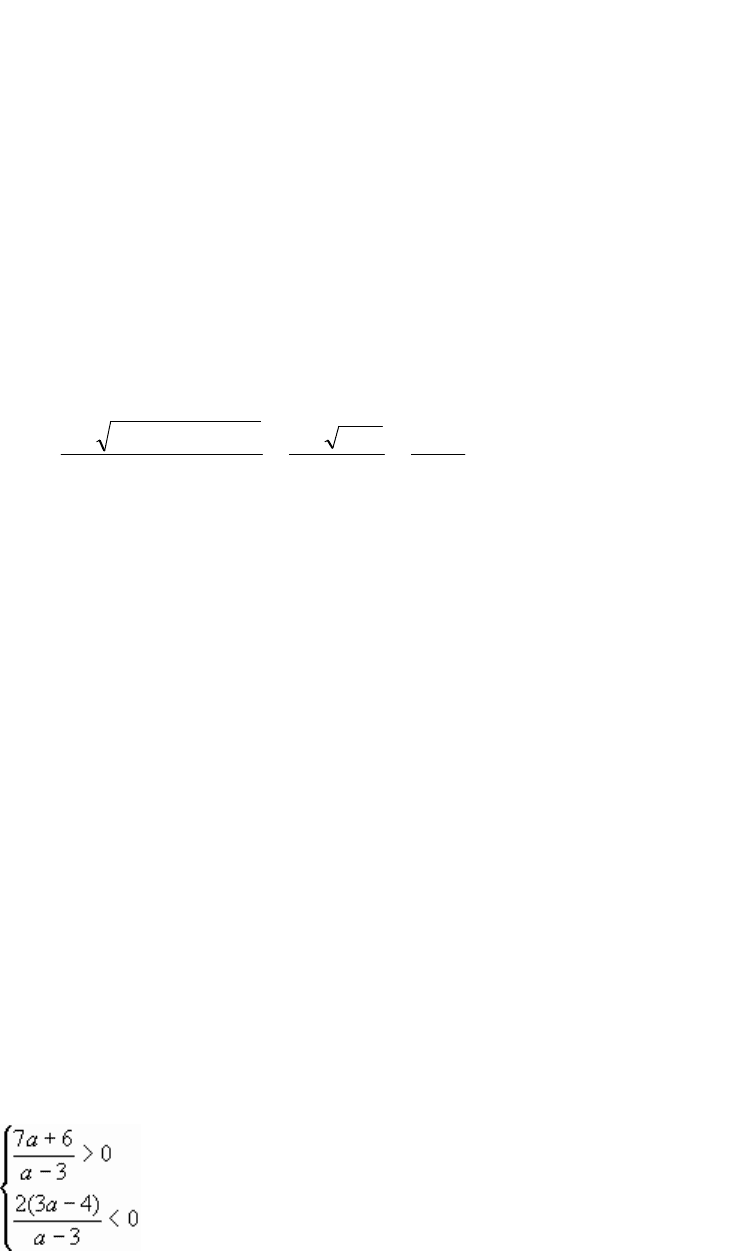
II. Практическая часть
Задачи, в решении которых используются комплексные числа.
1. Комплексные числа и уравнения
1).Из курса алгебры основной школы нам известно, что квадратное уравнение
,0
2
cbxax
a
0,
с действительными коэффициентами a, b, c имеет два различных
действительных корня, если его дискриминант D =
acb 4
2
– положительное
число. Если D = 0, то уравнение имеет единственный корень. Если же D < 0, то
мы обычно говорили так: корней у этого уравнения нет ( или, более точно:
квадратное уравнение не имеет действительных корней).
Одно из преимуществ комплексных чисел перед действительными числами
состоит в том, что во множестве C можно находить корни любых квадратных
уравнений.
Пример 1. Решить уравнение
05,83
2
zz
Решение. Так как все арифметические операции над действительными числами
вместе со свойствами этих операций имеют место и для комплексных чисел, то
сохраняется и формула корней квадратного уравнения. Воспользуемся ею:
2
53
2
253
2
5,814)3(3
2
2,1
i
z
Ответ:
,5,25,1
1
iz
iz 5,25,1
2
Пример 2. Решить уравнение
01
4
z
Решение. Разложим левую часть на множители:
iz
z
z
z
zz
z
4,3
2,1
2
2
22
4
;1
;1
;1
0)1)(1(
,01
Пример 3. (задание с параметром). Найти все действительные значения а,
при которых уравнение имеет только комплексные корни.
(a – 3)z
4
– 2(3a – 4)z
2
+ 7a + 6 = 0
Решение
Заменим z
2
= t
Получим уравнение (a – 3)t
2
– 2(3a – 4)t + 7a + 6 = 0
Таким образом, это уравнение имеет два действительных корня t
1
, t
2
. Для того,
чтобы у исходного уравнения корни были комплексными, необходимо, чтобы
t
1
, t
2
были отрицательными.
По теореме Виета, если t
1
и t
2
– отрицательные, то
Ответ: решений нет.
24
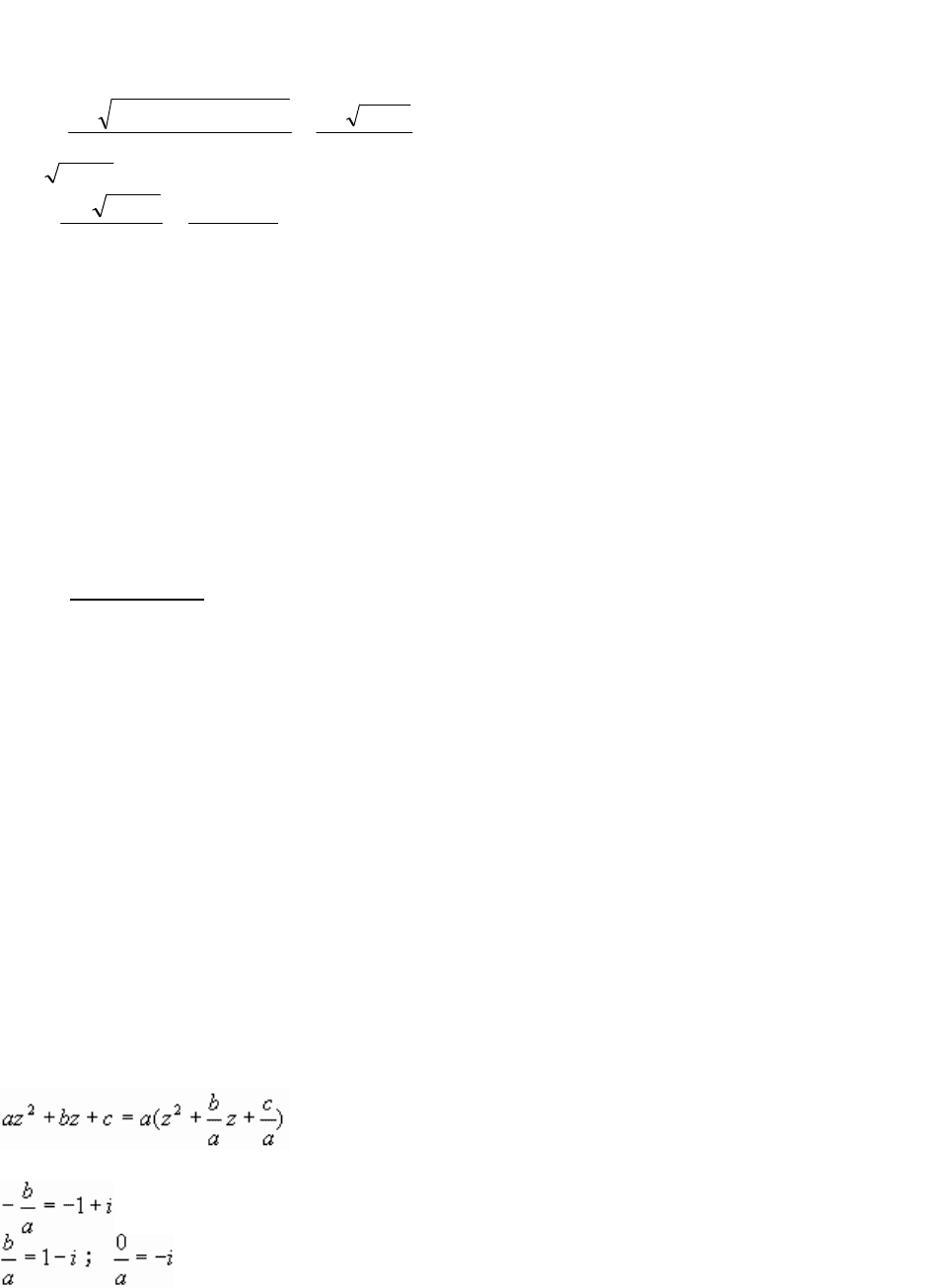
Пример 4. (Квадратное уравнение с комплексными коэффициентами).
Решить квадратное уравнение
01
2
iizz
Решение. По формуле получаем:
2
43
2
114
2
2,1
ii
iii
z
Но
ii 243
Поэтому
izzОтвет
iz
z
iiii
z
1,1:
1
1
;
2
)2(
2
43
21
2
1
2,1
Как обычно, у формулы корней квадратного уравнения есть полезные
следствия.
Теорема. (О разложении квадратного трехчлена на линейные
множители).
Если z
1
и z
2
– корни квадратного уравнения
))((0
21
2
zzzzacbzaz
Пример 5. Разложите квадратный трехчлен z
2
–iz–1+i на множители.
Решение:
Корнями квадратного трехчлена z
2
–iz–1+i являются числа 1 и –1+i. Р
Значит, z
2
–iz–1+i =(z–1)(z+1–i).
2). Задача, связанная с геометрической интерпретацией
комплексных чисел.
Пусть Р(z) – многочлен второй степени. Известно, что его корнями
являются числа -1 и i, а Р(0) = 2. Изобразите на комплексной плоскости
множество всех комплексных чисел, таких, что P(z) – действительное
число.
Решение.
Заменим многочлен второй степени в общем виде на b.
P(z) = az
2
+bz + c.
Т.к -1 и i – корни, то по теореме Виета
P(z) = a(z
2
+ (1-i)z – i)
z = x + yi
25
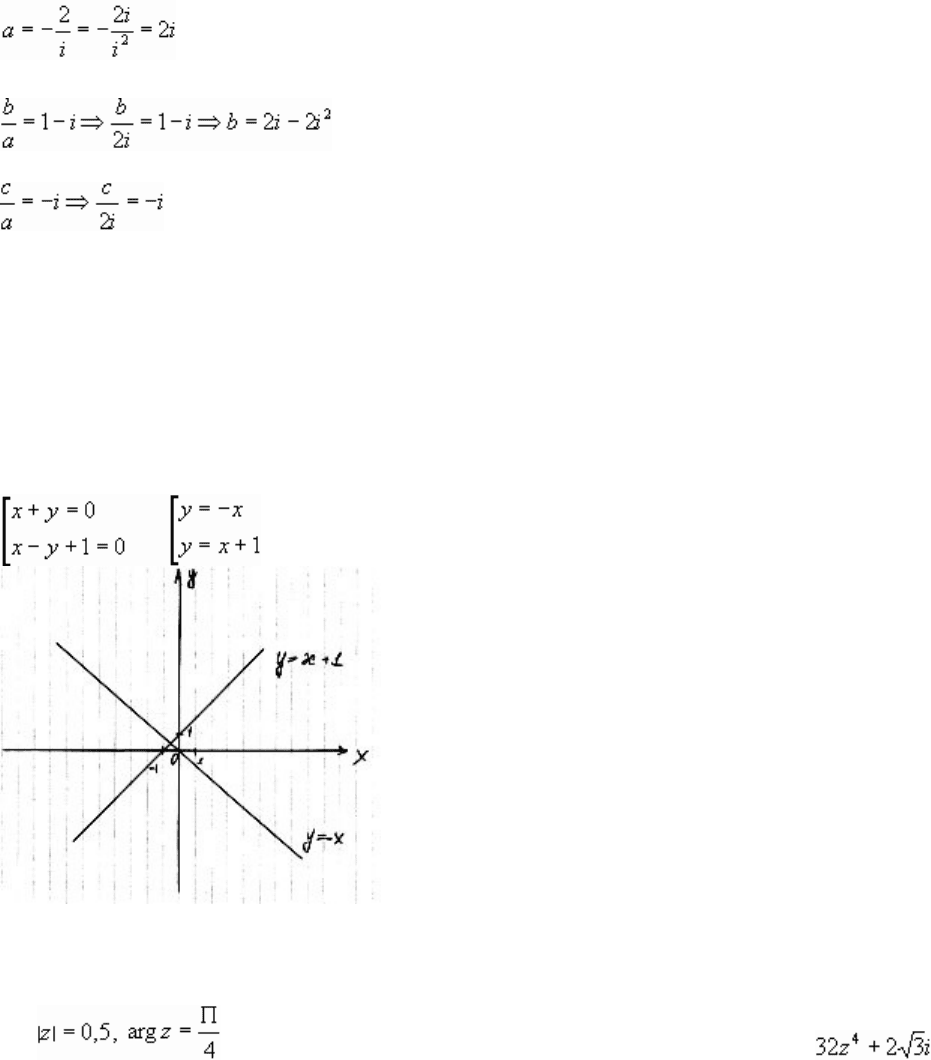
т. к P(o) = 2, то
P(0) = а(0+ 0 – i)
а( – i) = 2
; a = 2i
Тогда имеем
b = 2i + 2
; c = – 2i
2
; с = 2
P(z)= P(x + yi)= 2i(x + yi)
2
+ (2i + 2)(x + yi) + 2=
= 2i(x
2
+2xyi + y
2
i
2
) + 2xi + 2x + 2yi
2
+ 2yi + 2=
= 2x
2
i + 4xyi
2
– 2y
2
i + 2xy + 4x + 2yi
2
+ 4yi +2=
= (– 4xy + 2x + 2 – 2y) + (2x
2
– 2y
2
+ 2x + 2y)i
Т.к. по условию P(x + yi) – действительное число, то
x
2
– y
2
+ x + y = 0
(x – y)(x + y) + (x + y) = 0
(x + y)(x – y + 1) = 0
Задачи, связанные с действиями над комплексными числами.
3). . Найдите модуль и один из аргументов числа
Решение.
26
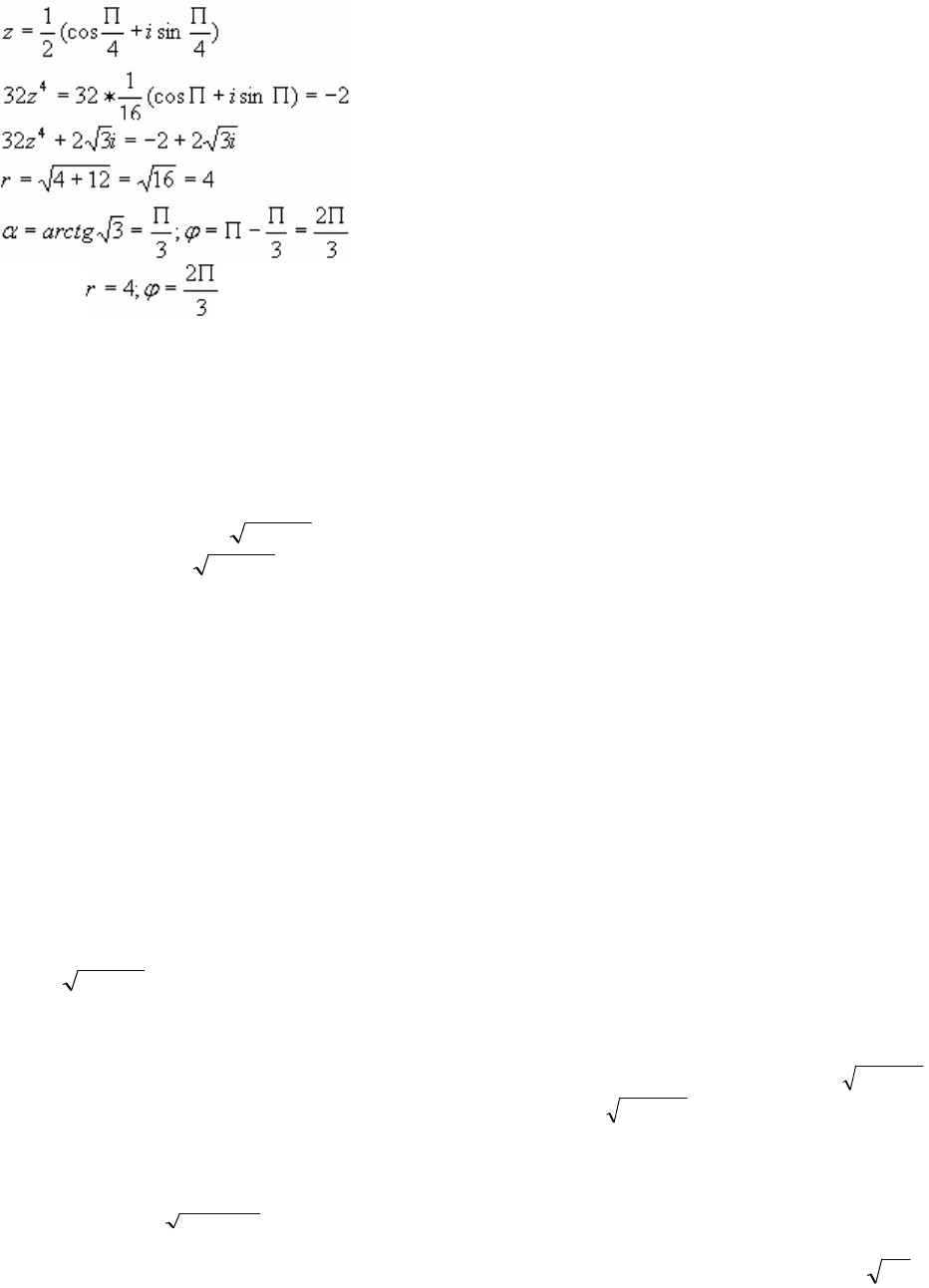
Ответ: 1
4) Найти действительные числа х и у, если (5х – 3у) + (х – 2у)i = 6 + (8 – x +
y)i.
Решение. Используя условие равенства комплексных чисел, получаем
Из этой системы определяем неизвестные х и у: х = -2/3, у = -28/9.
5)Извлечь корень
i125
Решение. Пусть
i125
= x + yi. По определению корня имеем (x + yi)
2
= 5 + 12i
или (x
2
– y
2
) + 2xyi = 5 + 12i, откуда получаем систему
Возведя оба уравнения в квадрат и сложив их, получим (х
2
+ у
2
)
2
= 25 + 144 и х
2
+ у
2
= 13.
Тогда из системы определим
неизвестные х и у: х = +-3, у = +-2.
Из второго уравнения системы следует, что знаки у х и y совпадают. Поэтому
х
1
= 3, у
1
= 2; х
2
= -3, у
2
= -2.
Итак
i125
имеет два значения 3 + 2i и -3 – 2i.
6). На множестве комплексных чисел решить уравнение z
2
+ |z| = 0.
Решение. Пусть z = x + yi. Тогда z
2
= (x + yi)
2
= (x
2
– y
2
) + 2xyi, |z| =
22
yx
, и
данное уравнение можно записать в виде (х
2
– у
2
+
22
yx
) + 2хуi = 0.
Последнее возможно тогда и только тогда, когда
Из второго уравнения системы (*) следует, что либо х
= 0, либо у = 0. Если х = 0, то первое уравнение (*) принимает вид –у
2
+
2
y
= 0,
т.е. –у
2
+ |у| = 0.
Так как у
2
= |у|
2
(по свойству абсолютной величины действительного числа), то
имеем: |y|
.
.
(|y| - 1) = 0, откуда либо |у| = 0, либо |у| -1 = 0.
Таким образом, при х =0 имеем: у
1
= 0,у
2
= 1, у
3
= -1.
27
;82
,635
yxyx
yx
.122
,5
22
xy
yx
;5
,13
22
22
yx
yx
(*)
0
,
2222
xy
yxyx
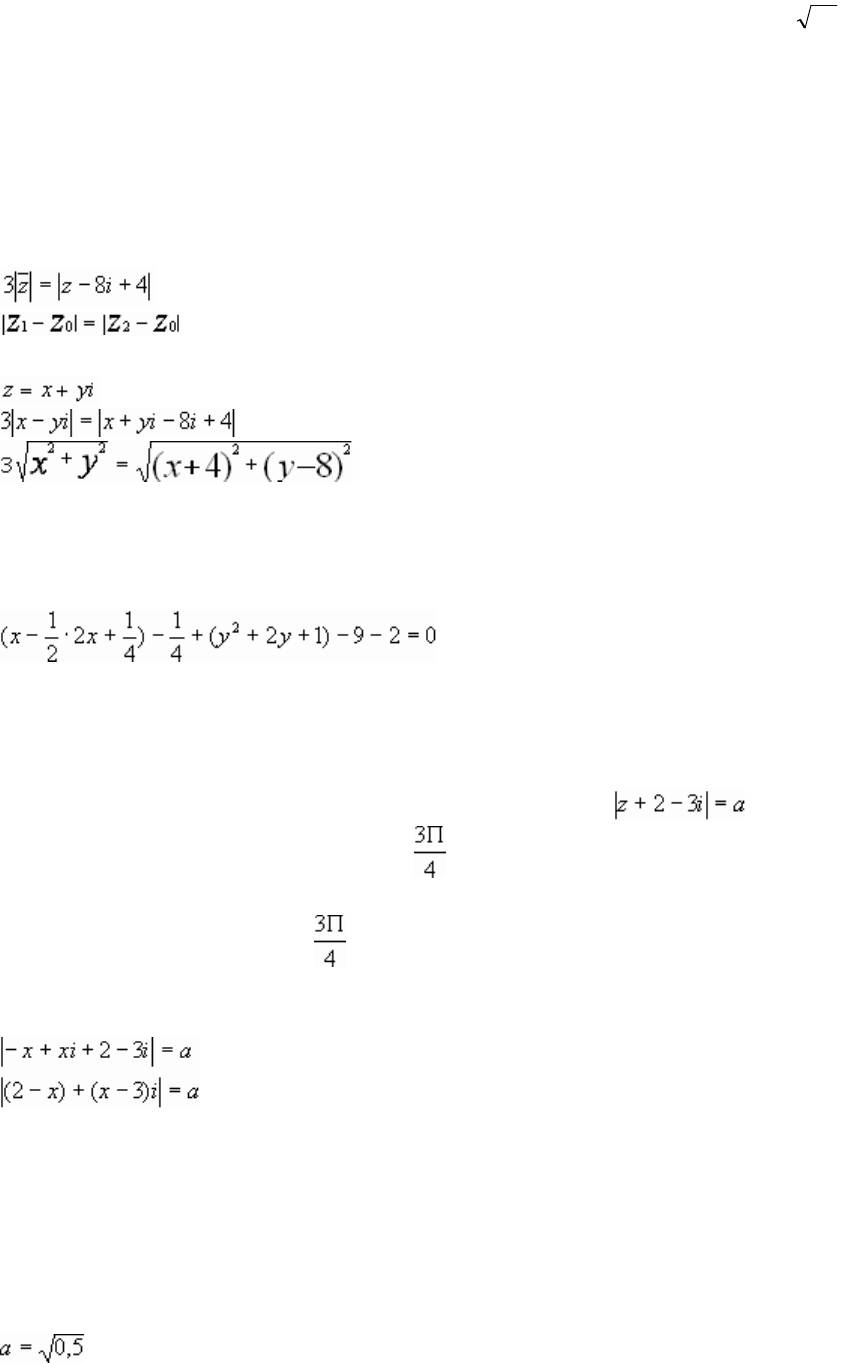
Если у = 0, то из первого уравнения системы (*) получим, что х
2
+
2
x
= 0, т.е. х
2
+ |х| = 0. Но это возможно только при х = 0 (ведь х – действительное число.)
Итак, данное уравнение имеет три корня: z
1
= 0, z
2
= i, z
3
= -i.
7) Задачи, связанные с решением различных уравнений,
содержащих комплексные переменные.
Множество Е состоит из всех комплексных чисел z, таких, что,
. Найдите все такие числа z
о
, что для любых z
1
и z
2
из Е
Решение.
9х
2
+9у
2
= (х+4)
2
+ (у-8)
2
9х
2
– х
2
– 8х – 16 + 9у
2
– у
2
+ 16у – 64 =0
8х
2
– 8х – 16 + 8у
2
+ 16у – 64 =0
х
2
– х – 2 + у
2
+ 2у – 8 =0
(х – 0,5)
2
+ (у + 1)
2
= 11,25
Окружность с центром (0,5; –1)
Ответ: z
о
= 0,5 – i
8). Среди всех комплексных чисел z, таких, что , есть ровно одно
число, аргумент которого равен . Найдите это число.
Решение.
Т.к. аргумент равен , то его действительная и мнимая части
противоположны. Причём действительная часть со знаком “-”, а мнимая “+”,
тогда z = – x +xi, x > 0
(2 – x)
2
+ (x – 3)
2
= a
2
4 – 4x + x
2
+ x
2
– 6x + 9 = a
2
2(x – 2,5)
2
– 12,5 + 13 = а
2
2(x – 2,5)
2
= а
2
– 0,5
(x – 2,5)
2
= 0,5(а
2
– 0,5)
По условию ровно одно число удовлетворяет этому соотношению. Значит,
уравнение должно иметь кратный корень, что возможно только лишь приa
(а – число неотрицательное).
x = 5/2a = 2,5
Ответ: z = – 2,5 + 2,5i
28
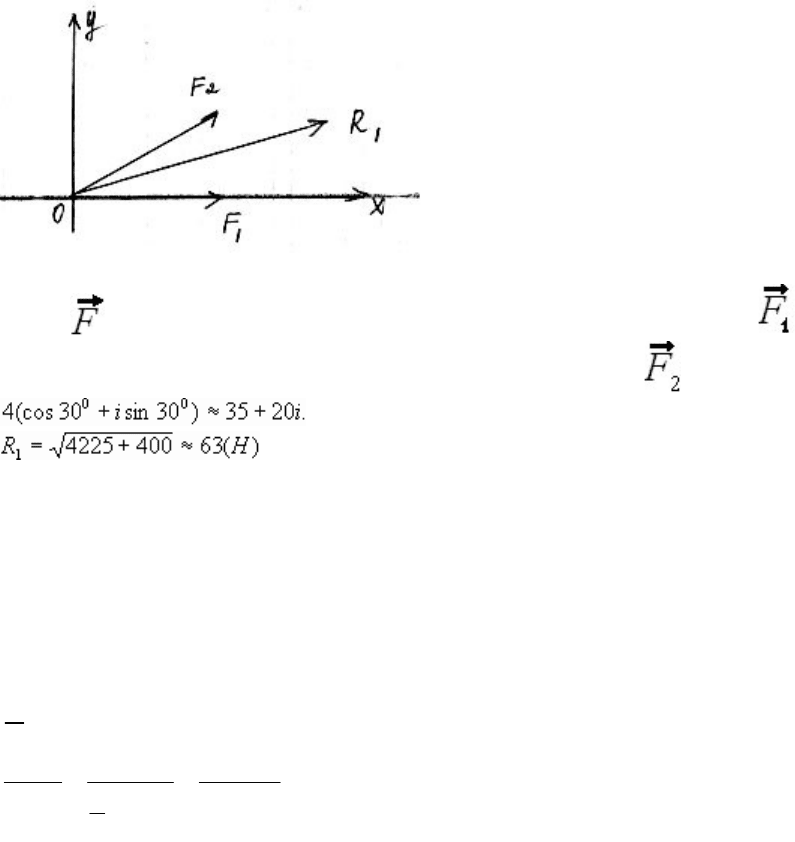
2.Применение комплексных чисел при решении физических задач
9). Найти равнодействующую двух сил в 30 Н и 40 Н, действующих на
точку тела под углом 30
0
друг другу.
Решение
Будем считать, что точка приложения сил совпадает с началом координат, а
сила сонаправлена с действительной осью. Тогда силе соответствует
действительное число 30, а силе комплексное число
Откуда модуль равнодействующей будет равен
3. Применение комплексных чисел в геометрии.
10) В результате поворота на 90° вокруг точки O отрезок AB перешел в
отрезок A
1
B
1
. Доказать, что медиана OM треугольника OAB
1
перпендикулярна прямой A
1
B.
Пусть координаты O, A, B равны, соответственно, 0, 1, b. Тогда точки A
1
и B
1
будут иметь координаты a
1
=i и b
1
=bi, а середина M отрезка AB
1
–координату m=
2
1
(1+bi). Находим:
.2
)(
)(2
1
2
1
0
1
i
bi
bii
bi
bi
m
ba
Это число чисто мнимое. На основании критерия перпендикулярности прямые
OM и A
1
B перпендикулярны.
29
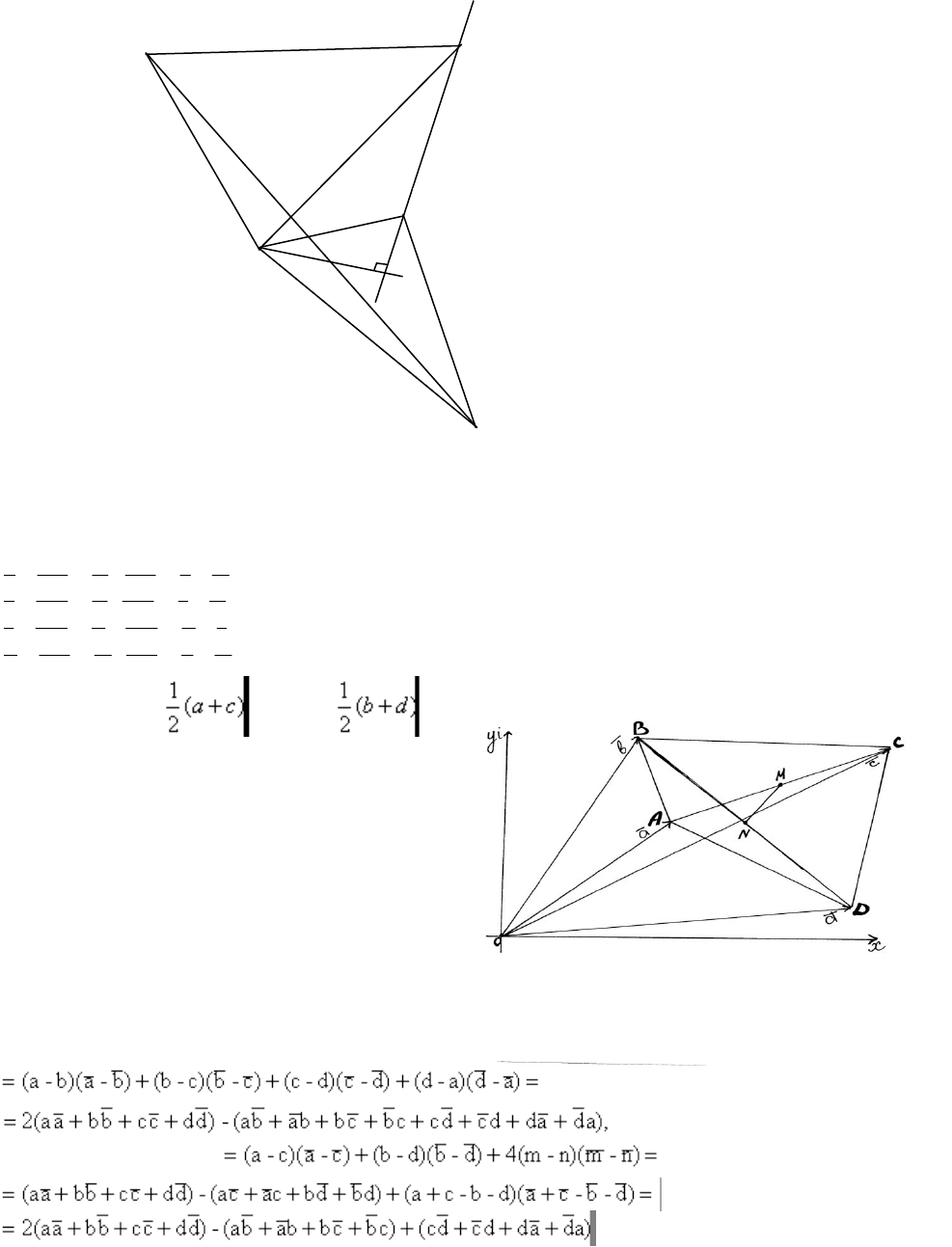
11) Точки М и N — середины диагоналей АС и BD четырехугольника
ABCD. (Рис.1) Доказать, что |AB|
2
+|BC|
2
+|CD|
2
+|DA|
2
= |AC|
2
+|BD|
2
+4|MN|
2
.
Решение. Пусть точкам A, В, С, D, М, N соответствуют комплексные числа а, b,
с, d, т, п.
.;
;;
;;
;;
daDAaDAd
cdCDdCDc
bcBCcBCb
abABbABa
Так как m = aи n = ,
тоa
|AB|
2
+|BC|
2
+|CD|
2
+|DA|
2
aaaaaaaaaa
|AC|
2
+|BD|
2
+4|MN|
2
.
Равенство доказано.
12) Доказать, что если в плоскости параллелограмма ABCD существует
такая точка М, что |MA|
2
+|MC|
2
=|MB|
2
+|MD|
2
, тo 1ABCD - прямоугольник.
B1
111
A1
B
M
O
A
30
