Рац М.В., Чернышев С.Н. Трещиноватость и свойства трещиноватых горных пород
Подождите немного. Документ загружается.

Была
предпринята
попытка
получить
информацию
о
х
а
р
акте
ре
взаимо
действия
соседних
тре
щ
ин
путем
корреляционного
анализа
посл
ед
о
вательн
осте
й
!
а/
I
i = 1, 2, 3,
...
(по-прежн
ем
у на
участках
равномерного
расположен
и
я
трещин).
Для
это
й цели
выполнен
расчет
ав
т
окорреляционных
функци
й
по
ря
ду
реа
лиза
ций
ПОСJIедователь
ностей
а/
,
содержащих
от
120
д
о
300
заме
ров.
rщ
(О
Q
1//1'
г:7lг
~
~з
~
1/1'1
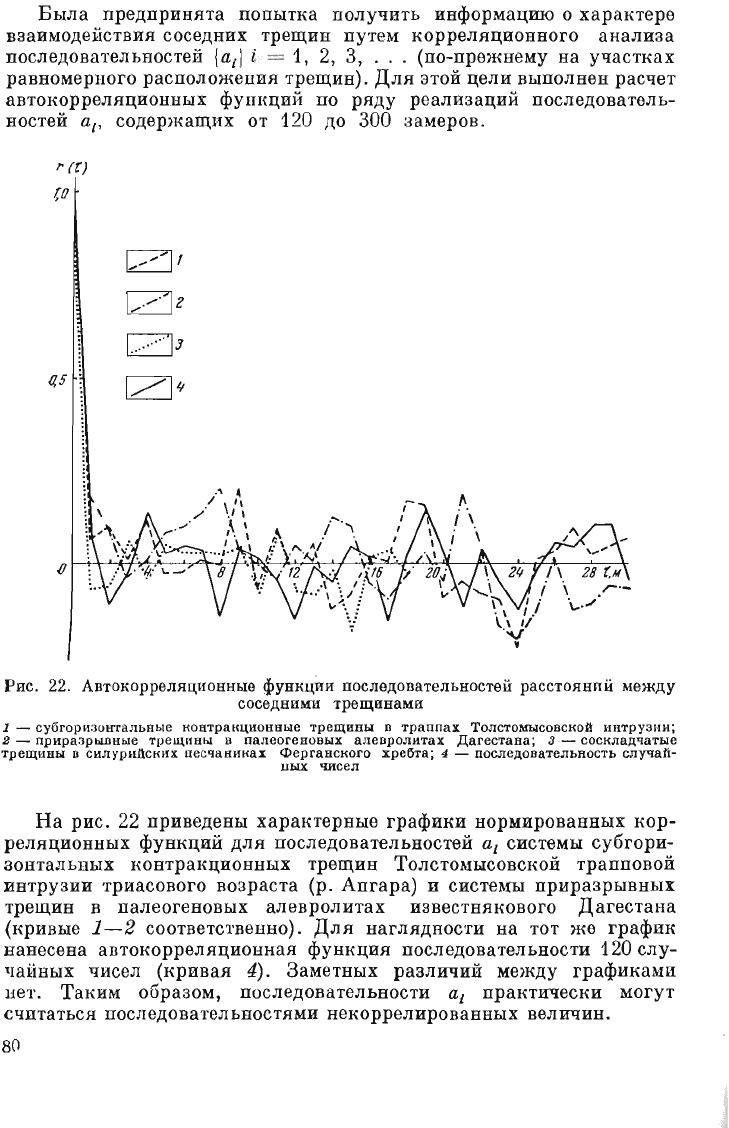
Рис.
22.
АвтокорреЛЯЦИОНlIЫе
функци
и
последовательност
ей
расстояний
между
соседними
трещинами
1 -
субг
о
риз
о
ат
а
льныс
к
о
нтраllционные
трещины
D
т
раппах
то
лстомыоDскойй
I1НТРУ
З
НИ;
2 -
ПРllра
з
рыоныс
ТРСЩIШЫ
D
палеогеновы
х
алевр
олит
ах
Дагестана;
3 ·-
соскладчатые
треЩ
l
lНЫ
в
СИ
Л
УР
IIЙ
СIIИХ
пе
с
чаниках
Ф
ерг
а
нског
о
хребта;
4 -
последова
тельн
ость
случай
-
ных
чис
ел
На
рис
.
22
приведены
характерные
графики
нормированных
кор
р
ел
яционных
функци
й
для
последовательностей
а/
системы
субгори
зонтаJIЬНЫХ
к
онтракционных
трещин
Толстомысовской
т
рапповой
ин
т
ру
зии
т
риасового
возраста
(р.
Ангара)
и
системы
прирэзрывных
трещин
в
паJIеогеновых
алевролитах
известнякового
Дагест
ан
а
(кривые
1
-2
соответственно).
Для
наглядности
на
тот
же
график
нанесена
а
вт
окорреляционная
функция
последова
теJI
ЬНОСТИ
120
слу
чайных
чи
сел
(кривая
4).
Заметных
различи
й
ме
жд
у
график
ами
н
е
т
.
Таиим
обр
аз
ом,
ПОСJIедовательности
al
практически
могут
считаться
пос
ледоватеJI
ЬНОС
Т
ЯМИ
нек
орр
еJIи
рованных
величин.
80

Приведенные
факты
требуют,
по-видимому,
д
альн
е
йших
экспе
римен
т
альных
и
теоретических
исследований.
Пока
мощно
предполо
жить
следующее.
Растрескивание
начинается
одновременным
раз
растанием
множества
трещинок,
расположенных
в
деформируемом
объеме
породы
равномерно
и
случайно
(разумеется,
речь
идет
о
макро
скопически
однородной
породе,
находящейся
под
д
ействием
макро
скопически
однородного
поля
напряжений).
В
силу
флуктуаций
расстояний
между
трещинами
на
некоторых
участках
образуются
при
этом
зоны
концентрации
напряжений.
В
этих
местах
рост
уже
существующих
трещин
может
ускориться,
и
здесь
же
(раньше,
чем
на
других
участках)
начинается
рост
следующего
поколения
тре
щин,
их
слияние
(на
второй стадии
разрушения)
и
в
дальнейшем
фор
мирование
разрыва.
Таким
образом,
процесс
разрушения
как
бы
уна
следуется.
Одновременно
происходит
повсеместный
рост
средней
длины
трещин,
в
ходе
которого
первоначально
прерывистая
сеть
трещин
переходит
в
непрерывную
(§ 3).
Даже
если
считать,
что
новые
тре
щины
при
этом
уже
не
ВОЗНИI<ают,
в
результате
роста
длины
трещин
густота
сети
увеличивается
и
рано
или
поздно
трещины
начинают
взаимодействовать.
Таким
образом,
наблюдая
непрерывные
сети
трещин
(а
именно
к
таким
сетям
относится
приведенный
выше
факти
ческий
материал),
мы
изучаем
существенно
видоизмененную
картину
результатов
первой
стадии
растрескивания,
для
которой
вообще-то
должна
быть
характерна
прерывистая
сеть
трещин.
Можно
предположить,
что
искажение
первоначального
гипоте
тического
экспоненциального
распределения
расстояний
между
сосед
ними
трещинами
в
системе
связано
именно
с
увеличением
длины
тре
щин
в
условиях
их
механического
взаимодействия.
Действительно,
поскольку
вокруг
трещины
возникает
зона,
частично
разгруженная
от
напряжений,
дальнейший
рост
близлежащих
трещин,
концы
кото
рых
достигают
разгруженной
зоны,
замедляется
или
прекращается
вовсе.
По
образному
выражению
М.
А.
Гончарова,
происходит
как
бы
взаимное
отталкивание
трещин.
В
результате
модальное
значение
расстояния
между
соседними
трещинами
смещается
вправо
(по
сравнению
с
исходным
экспоненциальным
распределением),
и
рас
пределение
приобретает
отчетливо
выраженную
левую
нисходящую
ветвь,
которая
и
наблюдается
в
действительности.
Приведенная
гипотеза
(которую
можно
назвать
гипотезой
фЛУК
туационного
растрескивания)
не
противоречит
наблюдаемым
фаI<там
и
позволяет
связать
их
с
имеющимися
в
фИЗИI<е
представ
ле
ниями
о
начальной
стадии
разрушения.
Стади
я
2.
С
гущение
JI
слияние
трещин.
М
.
В
.
ГЗОВСI<ИЙ,
разви
вавший
концепцию
формирования
тектонических
разрывов
путем
слияния
макротрещин
(1953, 1956, 1960),
указал,
что
в
этом
про
цессе
могут
участвовать
трещины
скола
и
отрыва,
раЗ
J
IИЧНО
ориенти
рованные
по
отношению
к
возникающему
разрыву.
Рацем
(1966б),
а
затем
М.
и.
ПогреБИСI<ИМ
был
получен
фактический
материал,
поз
воляющий
дать
статистический
анализ
процесса
сгущения
тр
щин
,
6
З
з
иае
1676 81

скола,
параллельных
возникающему
разрыву.
При
э т
ом
тренд
пара
'
метров
трещиноватости
по
направлению
от
относительно
сохран
ных
участков
к
разрыву
рассматривался
как
временной
-
от
пер
вой
ко
второй
стадии
разрушения
.
Как
видно
из
рисунка
14,
б,
.
по
мере
приближения
к разлому
среднее
расстояние
между
трещи
нами
заметно
уменьш
а
ется.
Исследование
закона
распределения
расстояний
между
трещи
нами
свидет
ел
ьствует,
что
во
всех
случаях,
за
исключением
узкой
приразломной
зоны,
это
распределение
может
быть
апцроксимировано
логарифмически
нормальной
моделью.
Нормальность
распределения
логарифмов
расстояний
между
трещинами
нарушается
лишь
вблизи
>
разлома,
где
распре
деление
становится
гетерогенным,
отражая
концентрацшо
трещин
в
л
окальные
линейно-вытянутые
вдоль
раз
лома зоны
(рис.
14,
а).
Бросается
в
глаза
удивительное
схо
дст
во
динамики
распределения
гус
т
оты
трещин
и
распределения
микро
деформаций
в
металлах
(см.
§ 12)
по мере
приближения
к
моменту
(или
месту)
разрушения
.
И
в
том
и
в
другом
случае
последовательно
наблюдается:
увеличение
степени
<<повреждению)
материала,
воз
растание
дисперсии,
локализация
повреждений
и
возникновение
гетероге
нн
ого
распр
еделен
ия.
По-видимому,
это
сходство
глубоко
заl{ономерно
и
отражает
статистическую
сторону
процессов
деформа
ции и
разрушения
.
При
этом
интенсивность
(густота)
трещиноватости
выступает
как
мера
остаточной
деформации
*.
Стадия
3.
Образование
и
разрастание
разрыва.
Процесс
быстрог
о
ра
з
растания
образовавшегося
при
слиянии
трещин
разрыва
в
геоло
гическом
масштабе
времени
мгновенен
и
не
оставляет
за
собой
сле
дов,
которые
можно
было
бы
анализировать.
Зато
именно
в
силу
своей
«мгновенностИ»
этот
процесс
может
наблюдаться
непосред
ственно.
Систематизация
результатов
наблюдений
за
разрывами,
выходящими
на
поверхность
зем
ли
при
сильных коровых
землетря
сениях,
совместно
с
данными
об
энергии
этих
землетрясений
позво
ляет
кое
-
что
узнать
об
этой
стадии.
Бо
ль
шая
часть
информации
получена
здесь,
естественно,
сейсмологами.
Поэтому
в
дальней
шем
изложении
мы
ШИрОI<О
пользуемся
сейсмологическими
дан
ными.
Как
указывал
о
сь
в
§ 11,
возникновение
и
разрастание
трещин
(разрывов)
длиной
l
сопровождается
выделением
энергии пропор
ционально
л,l2
/
4.
Согласно
существующим
представлениям,
земле
трясения
(по
крайней
мере
коровые)
возникают
в
результате
подви
жек
по
разрывам
ско
л
ового
типа.
Прослеживается
отчетливая
кор
реляционная
связь
энергии
сильных коровых
землетрясений
с
ампли
тудами
подвижек,
выходящих
на
поверхность
разрывов,
и
длинами
разрывов
(или
их
частей),
по
которым
фик
си
руе
тс
я
смещение
(Tocher,
•
Некоторые
исследователи
пре
дл
агают
рассматривать
густоту
трещин)tак
меру
интенсивно
с
ти
напряжеЮfЙ.
Это
предложение
неправомерно,
так
как,
если
в
породе
им
е
ются трещины,
8начпт
наrrряж
енп
я
достигали
предела
проч
ности
породы,
н
еза
ВПСl1МО
от
густоты
трещин.
82
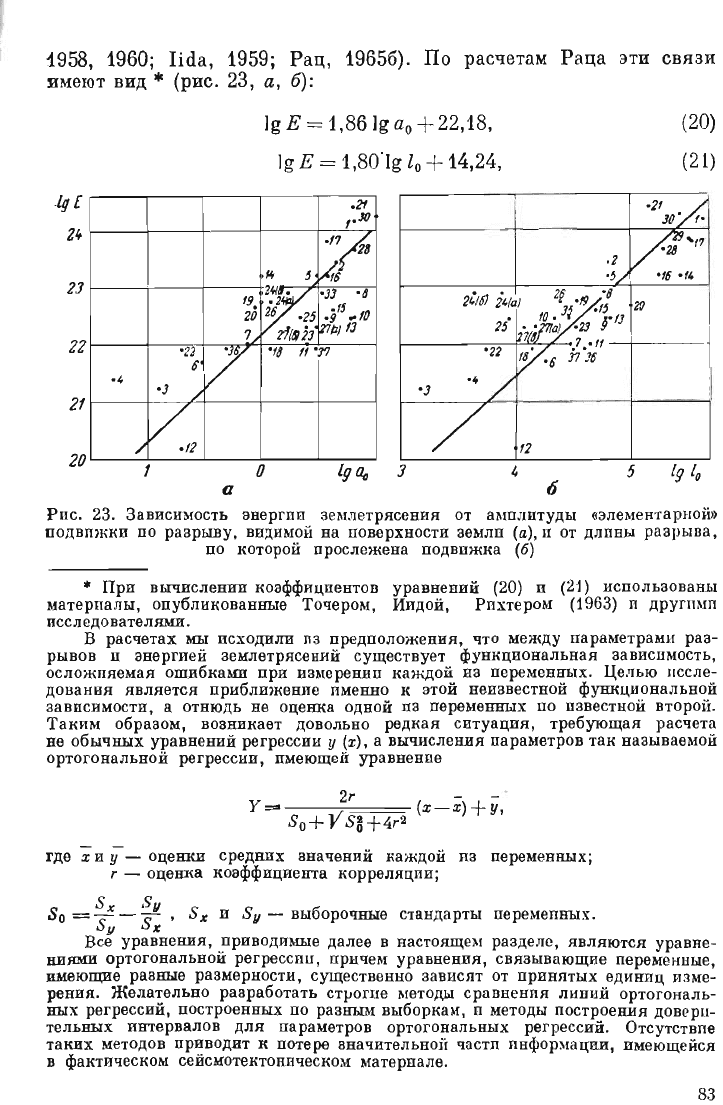
1958, 1960;
Iida,
1959;
Рац,
19656).
По
расчетам
Раца
эти свя зи
имеют
ВИД'"
(рис.
23,
а,
б):
JgE
21,
19
Е
= 1,86
1g
а
о
+ 22,18,
)g
Е
= 1,80'lg
lo
+ 14,24,
.21
"М
.1
(20)
(21)
.zt-ft
30'
"
'14
1+
23
;,t
$ ,6
'~/
/!"7
'16
'
I~
~
'
ЗЗ
'8
'!}
· 2
20
25
.25
.1$
'о
fЛ
"'~
7
nf!i2J
ы
f3
'
2/.
'7
"8
ff
'
1'1
6
,
~
,)
/
/
/
,,2
22
21
20
о
[g
og
1
а
2~
/67
г~{a
!
~
:
'19
,'~
20
,
10
,
г"
25
~
7r
jJл~
'2!
'
22~
,
.7,'"
18
' 6
J7
ЗВ
'
З
,+
/
/
f2
J
5
б
Р
ис.
23
.
Зависимость
энергии
землет
рясен
и
я
от
амплитуды
«элементарной»
по
д
вижки
по
разрыву
,
видимой
на
поверхности
земли
(а),
u
ОТ
дллпы
разрьша
,
по
которой
прослежена
подвижка
(6)
•
При
вычислении
коэффициентов
уравнений
(20)
и
(21)
использованы
материа
.lI
Ы,
опубликованные
Точером,
Иидой,
Рихт
е
ром
(1963)
и
другими
ис
следова телJDШ.
В
расчетах
мы
исходили
пз
предположения,
что
между
параметрам:и
раз
рыв
ов
и
энергией
землетрясений
существует
функциональная
эависимость,
осложняемая
ошибками
при
иэмеренип
каждой
из
переменпы..
Це
лью
ИСС
JJе
доваипя
является
приближение
именн
о
к
этой
неиэвестной
функциональной
зависимости,
а
отнюдь
не
оценка
одной
из
переменных
ио
известной
второй.
Таким
образом
,
возникает
до
вольно
редкая
ситуация,
требующая
расчета
не
обычных
уравн
ений
регрессии
у
(х),
а
вычисления
параметров
так
называемой
ортог
ональн
ой
регрессии,
имеющей
уравн
ени
е
2г
--
У
=
(х-х)+
у,
So+
VS3+4r
2
где х
и
у
-
оценки
ср
едних
значений
каждой
из
перемеННЫХj
r -
оценка
коэффициента
корреляции;
80
=
~;
-
~~
, S"
и
8
v
-
выборочные
стандарты
переменных.
Все
уравнения
,
приводимые
далее
в
настоящем
раз
деле,
являются
уравяе
НИJDШ
орто
гональной
регрессии,
причем
уравнения,
связывающие
перем
ениые,
имеющие
разные
размерности,
существенно
зависят
От
принятых
единиц
изме
рения.
Же
лательно
разработать
СТlJогие
методы
сравнения
линий
ортогональ
ных
регрессий,
построенных
по
разным
выборкам,
и
методы
построения
доверl1-
тельных
иитервалов
для
параметров
ортогональных
регрессий.
Отсу
тстви
е
таких
методов
приводит
к
потере
значительной
части
информации,
имеющейся
в
фактич
еском
сейсмотектоническом
материале.
83

где
Е
-
энергия
землет
рясений
в
эргах,
вычис
ленная
в
зависи
мости
от
магни
туды
землетрясения
М
по
форму
л
е
(Guten-
berg
, 1956):
19
Е
=
11
,8 +
1,5М;
d
o
-
максимальная
наблюденная
амплитуда
п
о
движки
на
поверх
ности
земли,
м;
lo -
длина
ра
з
рыва,
по ко
т
оро
й
прос
лежен
о
смеще-
ние,
М.
Коэффициенты
I\орреляции
равны
со
о
тветственн
о
0,73
и
0,
77
(
существенн
о
ОТ
ЛИЧНЫ
от
нуля
).
Заметим,
что
СО
О
J'ношение
(20)
близко
I{
р
езультатам
А.
Г.
Кон
стантиновой
1962, 1964),
изучавшей
связь
энергии
упругих
импуль
сов,
возбу
щ
даlOЩИ
ХСЯ
при
разрушении
гор
ных
пород
в
лабо
ра
тори
и,
с
размерами
т
рещ
ип
.
Эти
реЗУ
J
Iьтаты
хо
рошо
увязываютс
я
с
изл
о
женной
в
§ 11
теорией
трещин.
ЗаI{ОН
распределения
энергии
землет
ря
сений
(
заI\
ОН
повторяе
мости
земл
ет
р
ясений),
впе
р
вые
по
лученн
ый
Б.
Гутенбергом
и
Ч
.
Рих
те
ро
м
в
1954
г.,
также
сох
раня
ет
свою
форму
применительно
к
энер
г
ии
аи
устичеС
IШХ
импульс
о в
при
ра
з
р
у
ш
ении
обра
з
цо
в
(Виногра
д
ов,
1959, 1964; Mogi, 1962)
при
ПОД
ГО
Т
О
ВI\е
гор
ных
ударов
и
прим
ен
и
те
льн
о
к
энергии
горных
ударов
(Мысина,
1966)
19
N
=
а-
ylg
Е,
(22)
где
N -
чис
л
о
зе
м
лет
ря
сений
(ударов,
импульсов),
об
ладаю
щих
энергией
Е;
.
сх
и
у
-
э
мпирич
есние
к
оэффиц
иенты,
у
имеет
величину
поряд
на
0,4,
а
сх
колеблется
в
широ
ких
пределах
в
з
ави
сим
ос
т
и
от
уровня
сейсмичности.
Независимость
вида
ра
сп р
еделени
я
(22)
от
масштабов
разр у
ше
ни
я
является
важным
довод
ом
в
пользу
с
форм
ули
рованного
ра
нее
прин
ц
ипа
инвариантности.
Закон
ра
сп
р
еделения
(22)
в
с
илу
связ
ей
(21)
и
(20)
накладывает
HeI<oT
opble
огра
ничения и
на
в о
зм
о
жные
заноны
распр
еделени
я
длин
и
амплитуд
разрывов
,
растущих
в
хо
де
разруше
ния
.
В
частности,
из
пр
иведенвых
соотношений
следует,
ч
т
о
I\оличество
разрывов
д
о
лжн
о
монотонно
убывать
с
рос
том
их
длин
и
амп
литуд
.
Исходя
из
сходных
сообр
ажений,
это
подчеркива
л
М.
В.
Г
ЗОВС
I\
ИЙ
(1960).
Однаио
сделанный
вывод
нельзя
относить
к
т
р
ещинам
и
ра
з
р
ывам
,
фИI\
СИРУЮЩИМСЯ
в
зе
мной
коре
геологичеСI<ИМИ
методами.
Почему
I)TO
тю<,
станет
лсно
из
дальнейше
го.
Здесь
же
отм
ети
м
т
ольно,
ч
т
о
Фа
I\тичеСIюе
р
асп
р
еделение
длин
и
амплитуд
ра
з
рывов,
фИI\сир
уе
мых
гео
л
ог
ическими
мето
дами,
не
отличаетсл
от
л
огарифм
ичесни
н
ормаль
ного (Будько,
1958;
КУI<ЛИН
и
д
р.,
1964),
т
.
е.
имеет
маI<СИМУМ
и
левую
нисходящую
ветвь
.
84

Максимальная
амплитуда
смещения
при
землетрясениях
связана
с
длиной
в о
зникающего
разрыва (СаШеих,
1958; Amilien, 1963;
Рац,
1965б).
По
расчетам
Раца
*
19
lo
= 1,151g
ао
+ 4,25**.
(23}
Коэффициент
корреляции,
равный
0,57,
существенно
отличен
от
нуля.
Формула
(23)
пока
з
ывает,
что
длина
разрывов,
выходящих
на
поверх
ность
земли
при
сильных
коровых
землетрясениях,
в
среднем
в
104-
105
раз
больше
величины
максимального
смещения
по
ним.
Между
тем
геологам
известны
совсем
другие
соотношения:
длина
СI<ОЛОВЫХ
разрывов,
как
правило,
бывает
лишь
в
10-100
раз
больше
амплитуды
смещепия
крыльев
разрыва.
Д
етал
ьный
анализ
этих
соотношений
позволяет
наметить
(хотя
бы
в
самых
грубых
чертах)
общую
картину
формирования
тектониче
ских
разрывов.
Рассмотренные
выше
три
ста
д
ии
формирования
раз
рывов,
как
уже
отмеча
л
ось,
не
зависят
от
масштаба
разрушения:
они
характеризуют
процесс
разрушения
на
любом,
но
финсированном
уровне
.
Геологам
хорошо
известно,
что
крупные
разломы
имеют
длите
ль
ную
историю
развития,
а
не
образуются
«условно
мгновенно>)
(в
геологическом
маьштабе
времени),
причем
история
их
развития
не
може
т
быть
сведена
1<
трем
стадиям
разрушения
.
Если
геологиче
ской
истории
l<РУПНЫХ
разломов
посвящена
обширная
литература,
то
фи
зичеС
I<ИЙ
механизм
их
роста
практически
не
обсуждался.
Насколько
известно
автору,
лишь
в
работе
М.
В
.
ГЗОВСI<ОГО
(1960).
говорится
о
том,
что
рассмотренные
им
стадии
формирования
разры
вов
вкупе составляют
один «импульс
роста»
разрывов
и
что
«физи
ческая
историю>
разрывов
состоит
из
множества
таких
импульсов.
Развитие
этого
положения
Гзовского
лежит
в
основе
представляемой.
ниже
гипотетической
картины
(Рац,
1965б,
1968в).
Детальный
анализ
соотношения
длин и
амплитуд
тектонических
разрывов,
выполненный
А.
Кайе
(СаШеих,
1958;
Hel
·
ve
et
СаШеих,
1962)
и
Рацем
(1965а,
б
)
,
позволил
установить, что
между
длинами
и
амплитудами
разрывов
***
существует
соотношение,
аналогичное
·
(23),
но
с
существенно
иными
параметрами.
В
первом
приближении.
можно
принять
эту
зависимость
с
параметрами,
полученными при
анализе
сдвигов,
для
которых
связь
наиболее
тесная
и
параметры
вычислены
поэтому
наиболее
точн
о
19
l = O,831g
а
+ 1,56.
(24)
*
См.
сноску на
стр.
83.
**
В
сил~
большого
разброса
точек
относительно
линии
ортогональной.
р егрессии
коэффиц
ие
нт
при
19
ао
можно,
по-видимому
,
считать
несущественно>
ОТЛИ!lающимся
от
единицы.
***
Rайе
в
своем
анализе
не
расчленял
разрывы
по
типам
смещения.
Рац
ею
пропедено
исследование раздельно
для
сдвигов
(в
геологическом
смысле~
и
сбросов.
Отметим
сразу,
что
существовани
е
этой
связи
в
широком
диа
па
зоне
масштабов
(фю{тический
материал
имеется
для
разрывов
дл
иной
от
.десятков
метров
до
тысячи
Jшлометров)
является
вторым
серьез
ным
доводом
в
пользу
принятого
нами
принципа
инвариантности
*.
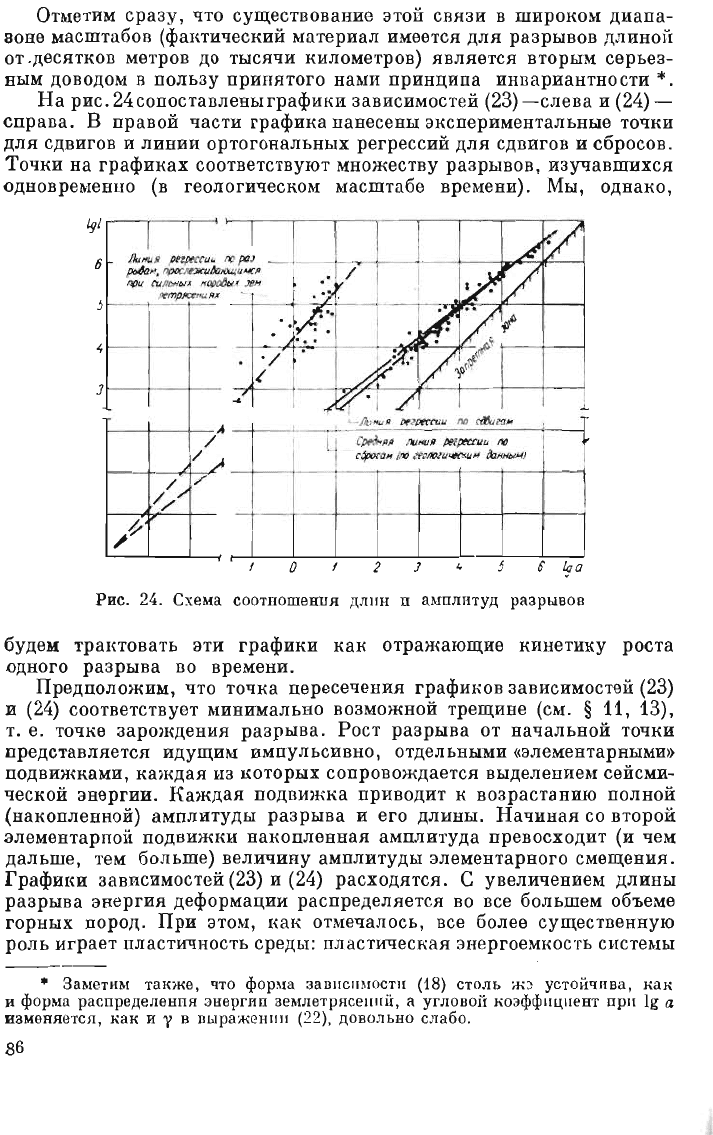
На
рис.
24сопоставленыграфики
зависимостей
(23)
-сле
ва
и
(24)
-
спра
ва.
В
правой
части
графика
нанесены
экспериментальные
точки
для
сдвигов
и
линии
ортогональных
р
ег
рессий
дл я
сдвигов
и
сбросов.
Точки
на
графиках
соответствуют
множеству
разрывов,
изучавшихся
одноврем
енно
(в
геологическом
масштабе
времени).
Мы,
однако,
'9'
I I
5
Ли
н
ия
pnpe«u"
ро4о".
fl(ЮCЛlЖu
40
I1(JU
сиЛЬНЫ
А
'
Х
ле
mР~
I#UЯ
А
J
А
/
/
/
/
///
;
~
./
('
о
L
L
PиНUII
Pi'1
1JttCl'UI/
no
tt1Ju
2t1
"
с"м"
рр
/I
/N
I/JP
/JIl
p«:r"
"
no
с
5р«
а
н
~
i!fl1lltJZu
чt(':<UН
iJa
ННbl
и
l
2 J
5
о
19a
Рис.
24.
Сх
ема
соотношения
Д
Л
IIН
n
а~mлптуд
разрыв
ов
будем
трактовать
эти
графики
как
отражающие
кинетику
рос
та
одного
разрыва
во
времени.
Предположим,
что
точка
пересечения
графиков
зависимостей
(23)
и
(24)
соответствует
минимально
возможной
т
р
ещине
(см.
§ 11, 13),
т.
е.
точке
зарождения
разрыва.
Рос
т
разрыва
от
начальной
точки
представляется
идущим
импульсивно,
от
дельными
«элементарными»)
подвижками,
каждая
из
которых
сопровождается
выделением
сейсми
ческой
энергии.
Каждая
подвижка
приводит
к
возрастаншо
полной
(накопленной)
амплитуды
разрыва
и
его
длины
.
Начиная
со
второй
элементарной
подвижки
накопленна
я
амплитуда
превосходит
(и
чем
дальше,
тем
больше)
величину
амплитуды
элементарн
ого
смещения.
Графики
зависимостей
(23)
и
(24)
расхо
д
ятся.
С
уве
л
ичением
длины
ра
зрыва
энергия
деформации
распределяе
тс
я
во
все
большем
объеме
горных
пород.
При
этом,
как
отмечалось,
все
более
существенную
ро ль играет
пластичность
среды:
пластическая
эне
ргоемко
сть
системы
•
3ам:
ети
ы
также,
что
ф
орма
эаВIIСI1МОСТlf
(18)
столь
ж
устойчива
,
как
и
форм
а
р
аспределения
эне
ргии
землетря
се
НIIЙ,
а
уг
ло
в
о
й
КОЭффllЦll
е
нт
Прl!
19
а
изменя
етс
я,
как
и
у
13
Dыраженпп
(
22
),
довольно
слабо.
86

1.
возрастает.
Сущес
твенную
роль
в
промежутках
между
по
движк
ами
начинает
играть
крип
-
вязкое
течение
вещества.
Если
скорость
деформац
ии
сохраняется
постоянной,
то
процесс
роста
разрыва
оказывается
нестационарным
(см.
также
Куз
нец
ова,
1962):
в
силу
рос
та
пластической
энергоемкости
время,
потребное
для
накопления
достат
очно
й
для
макрохрупкого
разрушения
(э
лемента
рной
по
движки)
упругой
энергии,
непрерывно
увеличивается.
ПО
ДВИilШИ
становятся
все
реж
е
.
Рано
или
поздно
(в
соответствии
со
скоростью
деформации)
процесс
полностью
переходит
в
вязкое
течение,
нарушаемое
ростом
д ругих,
более
мелких
разрывов.
Увеличение
относительной
ро
ли
пластической
деформации
с
ростом
величины
разрывов
выражается
в
нелинейности
зависимости
(24)
в
натуральном
масштабе
:
чем
длиннее
ра
з
рыв,
тем
большей
в
среднем
ока
зывается
его
амплитуда
по
сравненшо
с
длин
о
й.
Если
для
мелких
разрывов
(l
~
1
IC.М)
a/l
~
1/100,
то
для
самых
крупных
(l
~
1000
IC.М)
a/l
~
1/10
и
более.
Частота
элементарных
подвижек, как
и
приращение
длины
и
амплиту
д
ы
разрыва
при
каждой
из
них,
опр
еделяется
в
основном
скоростью
деформации:
чем
выше
скорость,
тем
быстре
е
скапли
вается
необходимая
для
подвижки
упругая
энергия,
тем
меньшая
часть
подводимой
к
системе
энергии
успевает
рассеивать
ся
в
резуль
тате
пластического
течения,
тем
большей
будет
элемен
та
рная
под
вижка
и
с
опровождающее
ее
землетрясение
(Гзовский,
1963).
наклоны
графиков
плотности
распр
еделени
я
энергии
землетрясений
.
(Вино
градов,
1962,
1964)
и
длин
трещин
(Кузнецов,
1964)
зависят
от
ско
рос ти
деформации
.
По-видимому,
аналогичным
образом
дело
обстоит
и
с
графиком
1 = f
(а),
наклон
которого,
как
показывает
фактиче
ский
материал,
несколько
меняется
для
разных
районов
земного
шара.
Различия
в
наклоне
графиков
1 = f
(а)
для
разных
районов
опре
деляются
скоростью
деформации:
чем
выше
скорость
деформации,
тем
меньше
роль
пластического
течения
и
тем
ближе
коэффициент
при
19
а
к
единице
.
В
пределе
при
«мгновенном»
хрупком
раврушении
большого
участка
земной
коры
график
1 = f
(а)
слился
бы
с
графиком
lo
= f
(ао).
При
этом
крупный
раврыв
возник
бы
О
ДН
ОaIПНО
(три
стадии,
однако,
сохранились
бы
хотя
и
сжатыми
во
времени)
и
имел
бы
амплитуду
порядка
1
/104
-1/100
от
своей
длины.
Однако
при
скоростях
деформации,
реально
присущих
литосфере,
при
существу
ющих
градиентах
скорости
современных
тектонических
движений,
рос
т
крупных
разрывов
происходит
обычно
длительное
время,
скла
дываясь
из
большого
количества
элементарных
подвижек
и
крипа
.
Кроме
того,
в
ходе
развития
может
наступить
момент,
когда
дальней
ший
рост
разрыва
будет
происходить
(<по
частям».
Де
йств
ительно,
длина,
по
которой
прос
лежива
ется
элементарная
подвижка,
!{ак
правило,
не
превосходит
первых
сотен
километров
(максимально
43511:.",
при
землет
рясении
в
Сан-Франциско
в
1906
г.).
Между
тем
полная
длина
сейсмогенных
разрывов
часто
превосходит
1000
11:.",
(сдвиг
Сан-Андреас)
.
Такая
ситуация,
по-видимому,
характерна
87
.в
особенности
для
случаев,
когда
снорость
деформации
в
ходе
геоло
rической
истории
уменьшается.
Из
приведенных
соображений,
в
частности,
вытекает, что
ампли
'
туд
а
смещения
по
разрывам
не
постоянна
по
их
длине,
а
должна
убывать
от
максимума
до
нуля
на
его
нонцах.
Как
правило,
максимум
.
должен
располагаться
где-то
в
ср
е
дней
части
разрыва
(Буртман
и
др.,
1963;
Ри
з
ниченко,
1966;
Рац,
1965).
Рис.
25
свидетельствует
о
непро-
тиворечивости
этого
вывода
фактическому
материалу.
(При
иссле д
о
вании
корреляционных
связей
длин
и
амплиту
д
мы
по
возможности
.lПользовались
максималь
н
ыми
амп
л
ит уд
ами)
.
aJ/(Af~_
/
--
......
Ч
/
-~_
. /
............
2 _
...1
-
......
__
, .
--:--
...
О
!t
8
/2
15
20
2'1
28
а
I~ГГГтъ
О
!
JZ!t
o,!t/J
О,
72
О
Р
и
с.
25.
Амплитуда
смеще-
пия
по
разрывам
а
-
изменение
амп
л
ит
уд
ы
по
дли
не
сд
в
и
г
ов
:
1 -
по
ка р
т
е
Тра
с
вела
и
}{о
уп
а
,
2 -
по
да
н
н
ым
В.
Г
.
Триф
о
нова;
б
-
ра
с
пр
е
д
ел
ение ра
с
ст
о
яний
от
се
ре
дины
сброса
до
точки
,
где
ам
п л ит уд
а
д
о с
тига
е
т
максимум
а
(по
нар
т
е
В
у
дринг
а
и др
.
)
.
Пр
е
дстав
л
енная
]
{
артина
роста
разрывов
в
ц
е
лом,
по
лу
ч
е
нная
преимущественно
на
основе
анализа
фактического
геологического
материала
(с
привлечени
е
м
миним
у
ма
гипо
тез
и
некоторых
физиче
ских
соображений),
хорошо
коррелирует
с
!{онцепцией
«сейсмиче-
·
ского
течения
горных
масс»,
разви
в
аемо
й
в
после
д
нее
время
Ю.
В.
Риз
ниченно
(1965, 1966).
Согласно
этой
нонцепции,
«з е
млетрясения
-
·
слабые
и сильные
(и,
сл
е
довательно,
элементарные
подвижки
по
разрывам
-
М.
Р.)
представляю
т
кю{
бы
МИI{роструктуру
манро
·
скопичесни
]{ва
з
инепрерывного
течения
з
е
много
мат
е
риала
в
боль
.
ших
областях»
(Ризниченко,
1966,
стр.
13).
Концепция
Ризниченко
носит
преимущественно
модельный
характер
и
сопоставляется
с
фак
тами,
известными
в
сейсмо
л
огии.
Поэ
т
ому
совпа
д
ение
ре
зул
ьтатов
(хотя
бы
начест
вен
но
е
)
гео
л
огии
и
с
ейс
мо
л
огии
явля
етс
я
здесь
.с
ущес
т
венным
.

ЧАСТЬ
II
МОДЕЛИ
ТРЕЩИНОВАТОСТИ
И
ИХ
ИСПОЛЬЗОВАНИЕ
ДЛЯ
ОЦЕНI{И
ИНЖЕНЕРНО-
ГЕОЛОГИЧЕСКИХ
СВОйСТВ
ТРЕЩИНОВАТЫХ
ГОРНЫХ
ПОРОД
•
Глава
4
МОДЕЛИ
ТРЕЩИНОВАТОСТИ
МАССИВА
ГОРНЫХ
ПОРОД:
§ 15.
Предварительные
замечания
Трещиноватость
гор
ных
пород
-
один
из
важнейших
фак
то
ров,
опре
дел
яющих
взаимодействие
инженерных
сооружений
с
литосфе
рой.
Сведения
о
т
рещиноватости
являются
поэтому
необходимым
исходным
материа
л
ом
при
обосновании
проектов
строительства
гидро
технических
сооружений,
карьеров,
шахт,
а
также
проектов
разра
ботки
ряда
месторождений
полезных
ископаемых:
месторождению
подземных
вод
,
нефти
и
газа,
содержащихся
в
трещинных
коллекто
рах;
месторождений
угля,
строительного
камня
и
Hel{
OTopblX
типов
рудных
месторождений.
При
всей
специфичности
задач
изучения
трещиноватости
в
каж
дом
случае
исследования
всегда
включают
ряд
общих
моментов,
обусловле
нных
трещиноватостью
как
о
дн
ой
из
форм
проявления
неоднородности
горных
пород.
В
силу
не
о
дн
оро
дн
ос
ти
объекта
иссле
дования
и
дискретности
геологических
наблюдений
решение
геологи-
·
ческих
задач,
и
в
том
числе
задач,
связанных
с
изучением
трещино
ватости,
часто
включает
три
этапа:
1)
оценку
тех
или
иных
сво
йств
(наних
именно
-
опред
еляетсЯi
поста
вленной
задачей)
гор
ных
пород
в
точках
наблюдений
*;
2)
интерполяцию
р
езультатов
наблюдений
между
ТОЧI{ами;
3)
оценну
того
или
иного
(опять
же
в
зависимости
от
поставленной..
задачи)
эффента
-
де
фор
мации
основания
сооружения,
запасов.
*
Речь
идет
о
так
называе~Iыx
«фпзичеСКIIХ
точках
»
.
Физической
точкой.
(пр
именительно
к
задачам
геологии)
следует
называть
lIекоторый
объем
в
мас
сиве
горных
пород,
достаточно
БО
JIЬШОЙ
по
сраnпеНllЮ
с
xapaKTepHЫМl
'
(
разме
р
ами
имеющихся
в
ыассиве
элементов
пеодпородности,
но
достаточно
малЫЙ1
по
сравнению
с
характерн:ьu.ш
размерами
в
решаеыой
задаче.
89
