Purser M. Introduction to Error Correcting Codes
Подождите немного. Документ загружается.


98
Proof
The
inequality
is
necessary because
of
the
prohibition
on
one
codeword being a
prefix
of
any
other
codeword.
Then
the
n 1 code words
of
length 1
"use
up"
r
U
- l)n I
of
the possible r
j
vectors,
because
all r
j
-
I
values for the
(j
- 1) symbols following
the
initial symbol
are
not
allowed. Similar reasoning applies
to
r
U
-
2
)n
2
,
and
so on.
But
from (A.3) we can
deduce
a whole series
of
necessary inequalities by
remembering
that
n j
=1=
O.
Therefore,
or
Discarding n j _
I'
n j _
2'
and
so on, successively
and
dividing by r each time, we
get
r
j
-
I
>n
j
_
1
+rn
j
-
2
+'"
+r
j
-
2
n
l
r
j
-
2
> n
j
_
2
+
rn
j
-
3
+
...
+r
j
-
3
n
l
(A.4)
The
series
of
inequalities (A.4)
are
a
consequence
of
(A.3).
But
given
that
(A.4)
hold, we
can
construct
an
immediate
code
by
choosing any n / <
r)
symbols for
the
strings
of
one
symbol in length. This leaves
(r2
-
rn
l
)
> 0 strings
of
length 2
available. Since
n
2
<
(r2
-
rn
l
)
we can pick any n
2
of
these
length
-2
strings
and
leave
r3
-
r(n
2
+
rn
l
)
> 0 strings
of
length
3 available from which to pick n
3
,
and
so on.
Therefore,
(A.3)
is
a necessary
and
sufficient condition for an
immediate
code.
Theorem A.2
If
L u
i
= L Vi = 1
then
i~
I,n
i~
I,n
(A.S)
i~
I.n
i~
I,n

99
Proof
Consider
the
inequality x
~
1 +
In
x,
where
In
is
the natural logarithm to base e
Putting
x =
uJu;,
we
have
uJu;
~
1 + In(u;/L';)
Multiplying
by
L';
and summing i = 1 to n gives
L
u;~
L u;+ L L';ln(u;/l';)
i~
l,n
i~
l,n
i~
l,n
or
so
i~
l,n
i~
l,n
Changing the base of the logarithms merely multiplies this inequality
by
a positive
constant. Therefore, (A.5) holds,
Theorem A.3
The average length,
L,
of an immediate code
is
greater than or equal to the
entropy
of
the source measured in bits
L
~
H(S)
L
is
defined as
L = L
pJ;
i~
l,n
where there are n source symbols to be encoded, and the
ith
source symbol has
probability
Pi and
is
encoded
as
a string of length
Ii
in the representational
symbols
0 and
1,
100
Proof
In
inequality
(A5)
set
to
give
or
But
L'i
=
Pi
_L
PJi+_L
Pi
lo
g2(!=
2-
I
J)Z_L
Pi
lo
g2(1/Pi)=H(S)
I-I,n
I-I,n
}-I,n
I-i,n
L
zH(S)
-log2(.
L
2-
1
,)
,~
I,n
L 2
-I,
= n 12-1 + n 2 2 - 2 + . . . + n j 2 -j
i~l,n
(A.6)
if there are n
i
strings
of
length Ii' which, using
(A3)
of
Theorem
A1
with r =
2,
gives
(A.7)
i=
l,n
Substituting
(A
7)
in
(A6)
gives
L
zH(S)
since
log2(.
L
2-
li
)'::;
0
,~I,n
Theorem
A3
states, setting M = n, that information in the form of source symbols
selected from an alphabet
of
M such symbols, can be compressed by encoding
each symbol as a binary string of
l;
bits per symbol, but that L has
H(S)
as a

101
lower bound. Shannon proposed a procedure for performing this encoding that
nearly achieves this bound, as follows.
1.
List the source symbols 5
i
in order
of
decreasing probability
Pi'
2.
Calculate for each 5
i
the number of bits Ii to represent it, using the
inequalities
3.
Calculate
Fi
= L
Pj
j~O.(i-])
and represent
Fi
as a binary fraction.
4.
Then
5
i
is
represented
by
the first ( bits of F
i
.
Thus, for an example, consider eight source symbols,
51
to 58' with probabilities as
listed in the first column of Table
AI.
Then
Ii'
F
i
, and the binary representation
of
5
i
can be read from the second, third, and fourth columns, respectively.
It
can be seen that this encoding produces an immediate code because the
length
is
such that for each new 5
i
the last bit
is
changed.
It
is
also clear that
is
bounded
by
So
H(5)
~L
< 1
+H(5)
In the above example
H(5)
= 2.73, while L = 2.78.
Table A.I
Pi
Ii
Fi
Bit String Representation
SI
1/4
2 0.00000
00
S2
1/4
2 0.01000
01
S3
1/8
3
0.10000
100
S4
1/8
3 0.10100
101
S5
3/32
4 0.11000 1100
S6
1/16
4 0.11011
1101
S7
1/16
4
0.11101 1110
S8
1/32
5 0.11111 11111

102
This
method
of
"Shannon
encoding"
is
not
the
best available.
For
example,
Huffman encoding applied to
the
above example would give L = 2.75.
For
our
purposes, however, it
is
sufficient to
note
that
L is
bounded
by
H(S),
and
coding
procedures
can
be
found
that
give L
near
to this
bound.
The
fact
that
this
compression from length log2
M to
near
H(S)
is
possible justifies
our
definition
of
redundancy.
A.2 CORRELATED SOURCES
So far we have assumed
that
the
source symbols
are
uncorrelated
in time, so
the
symbol
SI;
emitted
at
time
t(i
= 1
to
M)
is in no way affected
by
the
symbol
S(I_I),j
e~itted
at
time
(t
- 1). This
is
seldom
the
case,
and
it
is
necessary
to
extend
the
concept
of
entropy to
correlated
sources.
We
model a
correlated
source as a Markov process in which the probability
of
SI+
1 ; is conditioned by
the
state
of
the process as
determined
by the previous k
symbols emitted, Sl,il S(I_I),;2'" S(I-k+I),;k'
We
represent
this state
more
con-
cisely by
CI~j
(or
Cf
for
short
when
the
moment
in time
is
irrelevant).
Here
j
runs
from 1 to
Mk
if
the
i
run
from 1
to
M. Thus, we
represent
the conditional
probability
of
SI+I,; given
the
state
CI~j
as
The
entropy
of
such a
correlated
source is defined as
H(S)
=H(S)
=
"Lp(CnH(Cn
(A.8)
where
Thus,
the
entropy
of
the
source
is
the
average, weighted by
the
probability
of
the
states,
of
the
normal
entropy
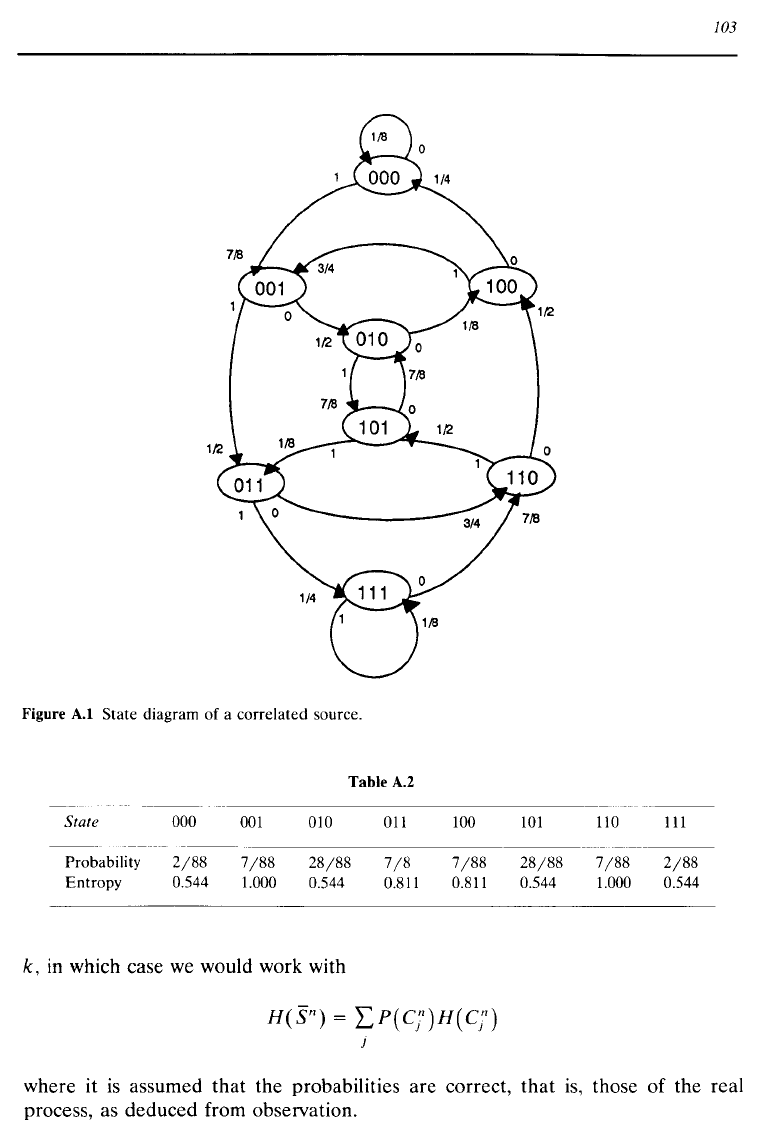
associated with each state. Figure
Al
illustrates such
a
correlated
resource with M = 2
and
k = 3, so
that
there
are
eight states, as
shown in Figure
Al.
The
transitional probabilities
are
also shown, so, for example,
POIOOO)
=
7/8.
It
is
easily shown
that
the
probabilities
and
entropies
of
the
states
are
as
shown in
Table
A2.
This gives
H(S)
= 0.659.
In
reality,
of
course, while we may guess
that
a source is
correlated,
we do
not know k. We might guess
that
the
depth
of
correlation
is
n symbols
rather
than
103
Figure A.I State diagram
of
a correlated source.
Table
A.2
~---
State 000
001
010
011
100
101
110
111
Probability
2/88
7/88
28/88
7/8
7/88
28/88
7/88
2/88
Entropy
0.544
1.000 0.544 0.811 0.811 0.544 1.000 0.544
k,
in
which case we would work with
where it
is
assumed that the probabilities are correct, that
is,
those of the real
process, as deduced from observation.

104
Theorem A.4
Proof
Clearly when
n
~
k H(sn) = H(S) because of (A.8). For n < k
H(Cn
= -
LP(S'+I)C;Jlog2
p(S'+I,iI
C
;J
by
Theorem A.2.
Therefore,
P(
CnH(
Cn
::;;
-
LP(S,+
l,i' S',il'" S'-n+ l,in)log2
p(
S,+
I)C;j
1)
i
Summing over all M
n
values of j
we
get
(A.9)
We can also consider n symbols at a time and ignore the correlation. This means
that the source
is
regarded as an uncorrelated source of Mk symbols. We
designate such a source
as
sn, and its entropy
is
called H(sn).
Theorem A.S
Proof
By
definition
H(sn)
= -
LP(Cnlog2
p(Cn
j
= -
LP(Cn[log2p(S,)C;_-I~j)
+ log2
P(C;_-II.
j
)]
j
= -
LP(
C,n_-/
j
) L
p(
S"iIC;_-/j )log2
p(
S"il
C;_-
I
I,j)
J
- L
LP(S',i,C;_-/j)log2P(C;_-I~j)
j i

105
So
(A.lO)
Theorem A.6
H(sn)/n
tends to
H(S)
as
n becomes large.
Proof
For n
~
k (the correlation length)
we
sum equations (A.1O) together, remembering
that
by
Theorem A.4, and get
Dividing
by
n gives
H(S)
+
[H(SI)
-
H(S)]/n
~H(sn)/n
~H(S)
+
[(k
-l)H(SI)
+H(SI)
-
kH(S)j/n
Now
H(SI)
= -
LP(ci,j)LP(S/+I,iI
C
},j)log2
P
(St+I)C},j)
j i
~
-
LP(
C},j)
LP(
St+
l,iIC},j
)log2
P(
St+
I,i)
j i
by
Theorem A.2. That gives

106
and since
H(SI)
~
H(S),
the above inequality for
H(sn)/n
becomes
H(S)
+a/n
~H(sn)/n
~H(S)
+ka/n
(A.11)
with a
~
O.
Therefore,
H(sn)/n
tends to
H(S)
as
n tends to infinity.
We can also show the next theorem.
Theorem A.7
H(sn)/n
decreases as n increases
Proof
H(sn)/n-H(sn+l)j(n+
1)
=
[i~
l~-l
H(Si)
+
H(SI)
J/n
-
[i~~n
H(Si)
+
H(
Sl)
J/(n
+ 1)
=
[i~l~-l
H(Si)
+H(SI)
J/n(n
+ 1)
-H(sn)/(n
+ 1)
=
[i~l~-l
H(Si)
+
H(SI)
-
nH(sn)
J/n(n
+ 1)
~O
Therefore,
H(sn)/n
decreases
as
n increases and,
by
Theorem A.6, tends to
H(S).
We can conclude from these theorems that modelling the source as a Markov
source will give
better
and
better
approximations to the real entropy
as
n increases
to
k (Theorem A.4). But, more important, if we do
not
model the correlation but
group the
symbols n at a time into "supersymbols" from an alphabet of M
n
symbols and treat them
as
independent
of
each
other
in time,
then
the entropy
per
symbol
H(sn)
/n
tends to the real entropy. This
then
is
a justification for
continuing to use compression techniques based on uncorrelated symbol strings,
provided they are applied to symbols grouped
n at a time. We see also that
Theorem A.3 holds with the new definition of entropy,
H(S),
if we consider
variable length encoding of our supersymbol strings of
n symbols.

and
In
our
specific example these theorems are illustrated by noting
that
H(
51) = 0.731
~
H(
52) = 0.730
~
H(
53) = 0.659 =
H(
S)
H(
SI)
= 1
~
H(
S2)/2
= 0.866
~
H(
S3)
/3
= 0.821
~
H(
S4)/4
= 0.780
H(S2)
= 1.732
=H(SI)
+H(5
1
)
H(S3)
= 2.463 =
H(S2)
+
H(5
2
)
H(
54) = 3.120 =
H(
S3) +
H(
53)
A.3 INFORMATION IN TRANSIT
107
We have seen how the information
generated
by
a source,
nH(5),
is
generally less
than
the
number
of
bits, n log2
M;
if
there
are
M symbols in
the
alphabet,
H(5)
is
the
average information
content
of
each symbol in bits,
and
n symbols
are
sent.
The
information
rate
is,
therefore, [H(S)]r bits
per
second, where r
is
the
symbol rate,
that
is,
the
number
of
symbols
per
second.
When
this information
is
actually transmitted, it may become subject to
further losses, due to errors.
We
model this
by
considering the probabilities
of
transmitted symbols
Xi
(i
= 1 to
K)
after
observing received symbols
Yj
(j
= 1
to
K),
which are the
Xi
with some corruptions. See Figure A.2.
The
symbols
here
are
the
representational symbols of
the
restricted alphabet into which
the
source
symbols
are
encoded. K = 2 normally.
The
information associated with
Xi
given
Yj
is
-log2
p(xi!Y),
where
p(xi!Y)
is
the
a posteriori probability
of
Xi' having
observed
Yj' We may define
as the average uncertainty about the source symbols remaining after viewing
Yj'
Transmission medium
Figure
A.2
Symbols being transmitted and corrupted.
