Прохоров С.А. Лабораторный практикум. Моделирование и анализ случайных процессов
Подождите немного. Документ загружается.

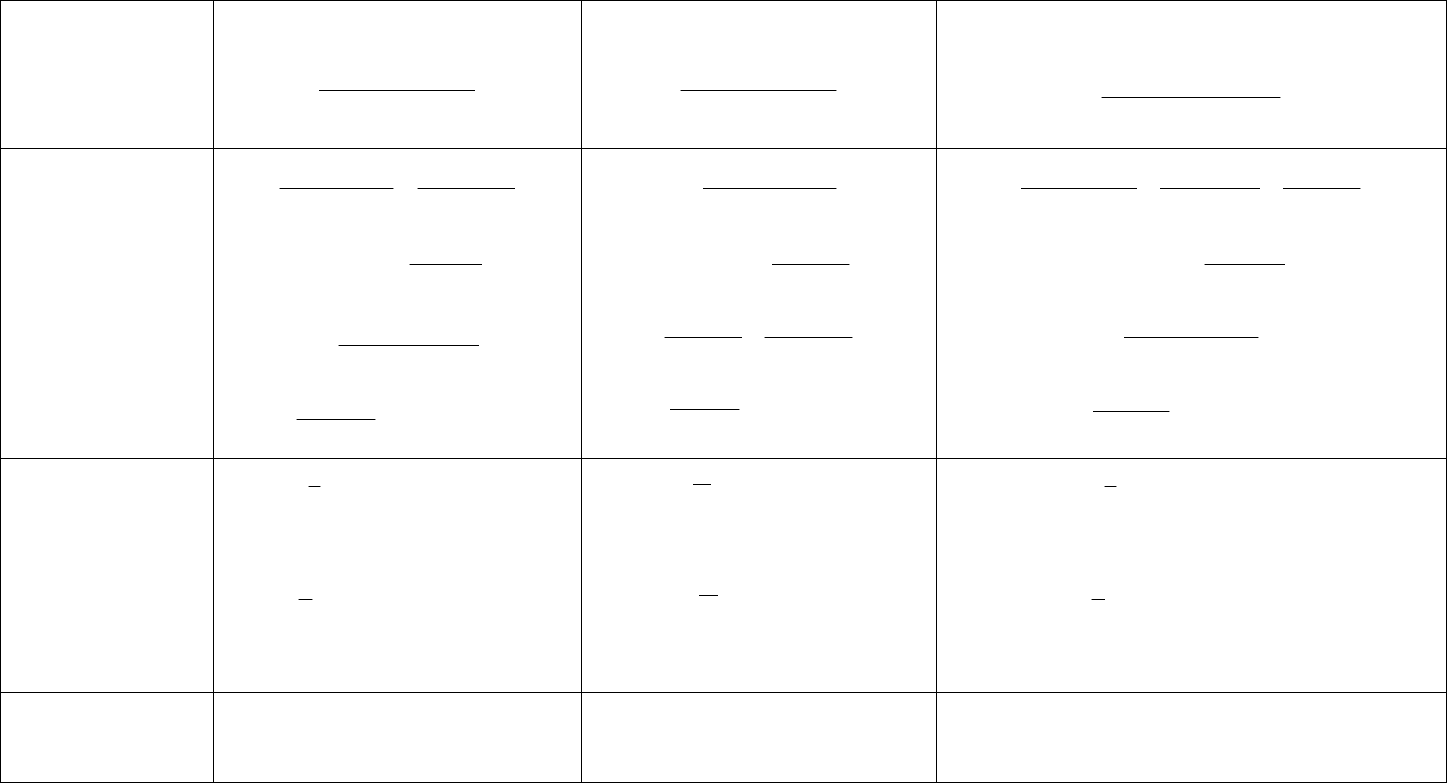
Приложение 11
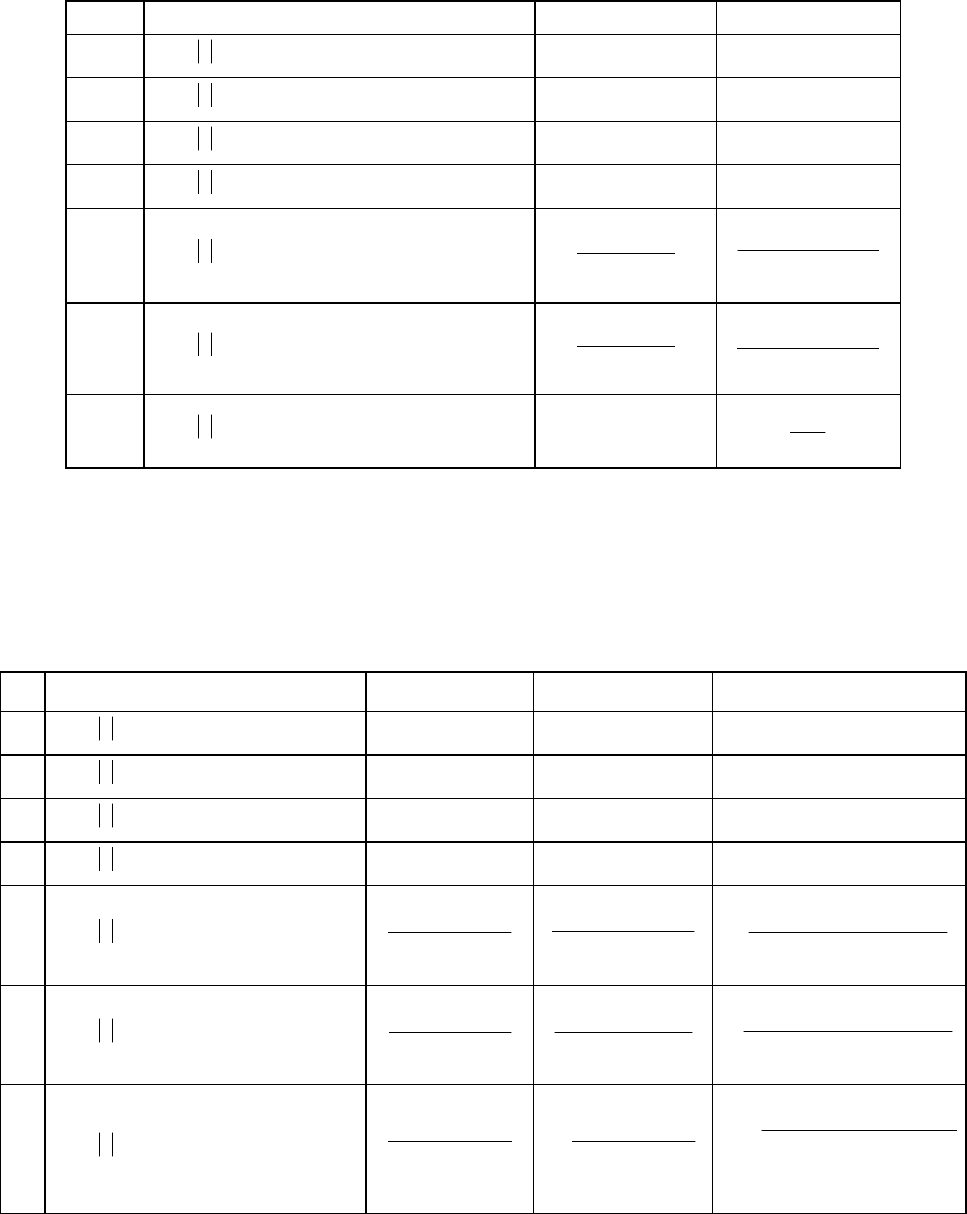
Производные для двухпараметрических функций распределения
Закон
распределения
β
∂
β
β
∂
1
)
2
,
1
,x(F
β
∂
β
β
∂
2
)
2
,
1
,x(F
β
∂
ββ
∂
2
1
)
2
,
1
,x(F
2
Симпсона
() ()
2
)(4
3
2
)(4
ab
a
j
x
ab
a
j
x
−
−
−
−
−
)
2
ba
xa(
+
<<
()
3
2
)(4
ab
j
xb
−
−
−
)bx
2
ba
( <<
+
()
3
2
)(4
ab
a
j
x
−
−
−
)
2
ba
xa(
+
<<
()()
3
)(8
2
4
ab
j
xb
ab −
−
−
−
)bx
2
ba
( <<
+
() () ()
2
4
3
)(16
4
2
)(12
abab
a
j
x
ab
a
j
x
−
+
−
−
−
−
−
)
2
ba
xa(
+
<<
()
4
)(24
ab
j
xb
−
−
)bx
2
ba
( <<
+
Лапласа
)(
)(
2
1
μ
μλ
−
−−
j
x
e
j
x
)x(
μ
>
)(
)(
2
1
μ
μλ
−
−
j
x
e
j
x
)x(
μ
<
e
j
x )(
2
μλ
λ
−−
−
)x(
μ
>
e
j
x )(
2
μλ
λ
−
−
)x(
μ
<
2
)(
)(
2
1
μ
μλ
−
−−
−
j
x
e
j
x
)x(
μ
>
2
)(
)(
2
1
μ
μλ
−
−
j
x
e
j
x
)x(
μ
<
Вейбулла
j
x
e
j
x
j
x
ln
α
β
α
β
−
e
j
x
j
x
α
β
α
−
)1(
2
ln
j
x
j
x
e
j
x
j
x
α
β
α
β
α
β
−
−
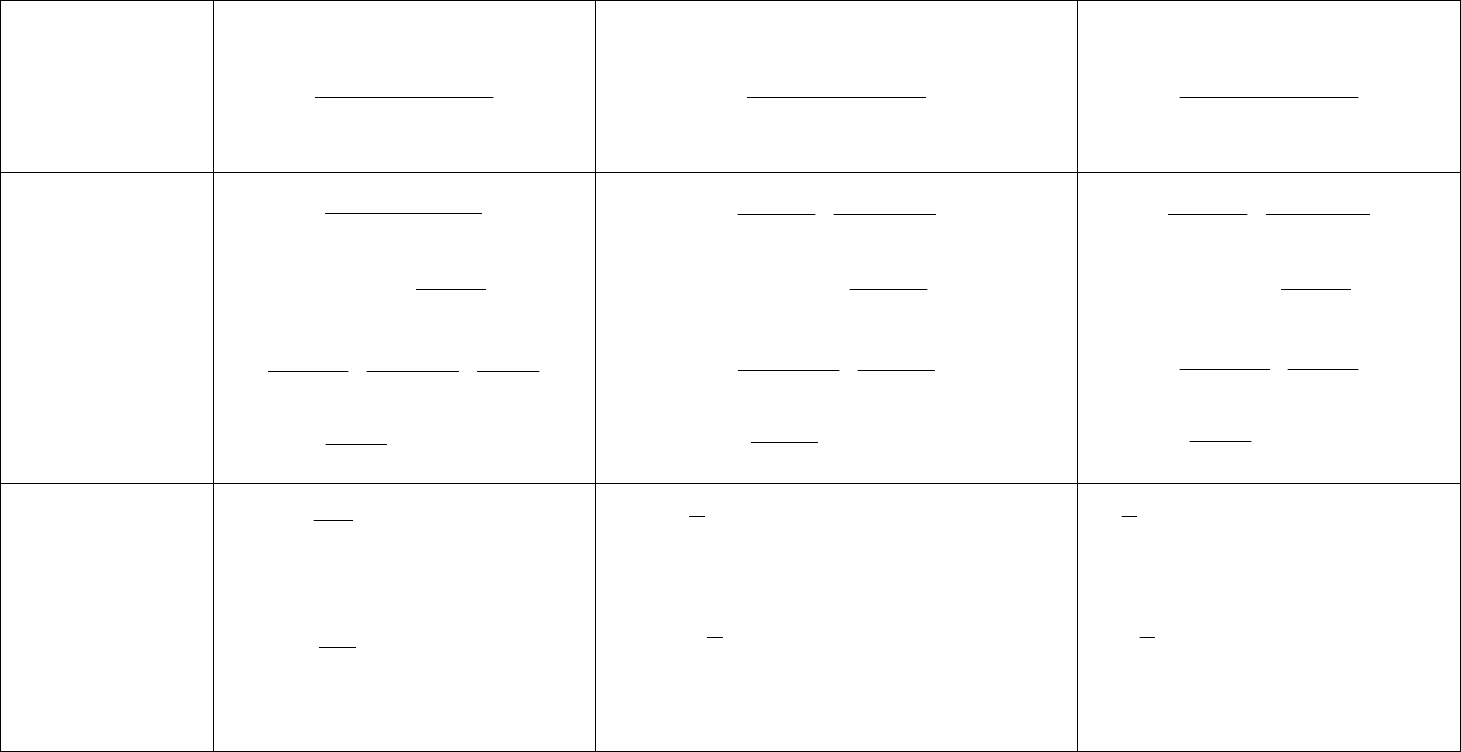
Продолжение приложения 11
Закон
распределения
β
∂
ββ
∂
2
2
)
2
,
1
,x(F
2
ββ
∂
ββ
∂
21
)
2
,
1
,x(F
2
ββ
∂
ββ
∂
12
)
2
,
1
,x(F
2
Симпсона
()
4
2
)(12
ab
a
j
x
−
−
)
2
ba
xa(
+
<<
() () ()
2
4
4
2
)(12
3
)(16
abab
j
xb
ab
j
xb
−
−
−
−
−
−
−
)bx
2
ba
( <<
+
() ()
4
2
)(12
3
)(8
ab
a
j
x
ab
a
j
x
−
−
−
−
−
)
2
ba
xa(
+
<<
() ()
3
)(8
4
2
)(12
ab
j
xb
ab
j
xb
−
−
−
−
−
)bx
2
ba
( <<
+
() ()
4
2
)(12
3
)(8
ab
a
j
x
ab
a
j
x
−
−
−
−
−
)
2
ba
xa(
+
<<
() ()
3
)(8
4
2
)(12
ab
j
xb
ab
j
xb
−
−
−
−
−
)bx
2
ba
( <<
+
Лапласа
e
j
x )(
2
2
μλ
λ
−−
−
)x(
μ
>
e
j
x )(
2
2
μλ
λ
−
)x(
μ
<
)1)((
)(
2
1
−−
−−
μλ
μλ
j
x
e
j
x
)x(
μ
>
))(1(
)(
2
1
μλ
μλ
−+
−
−
j
x
e
j
x
)x(
μ
<
)1)((
)(
2
1
−−
−−
μλ
μλ
j
x
e
j
x
)x(
μ
>
))(1(
)(
2
1
μλ
μλ
−+
−
−
j
x
e
j
x
)x(
μ
<
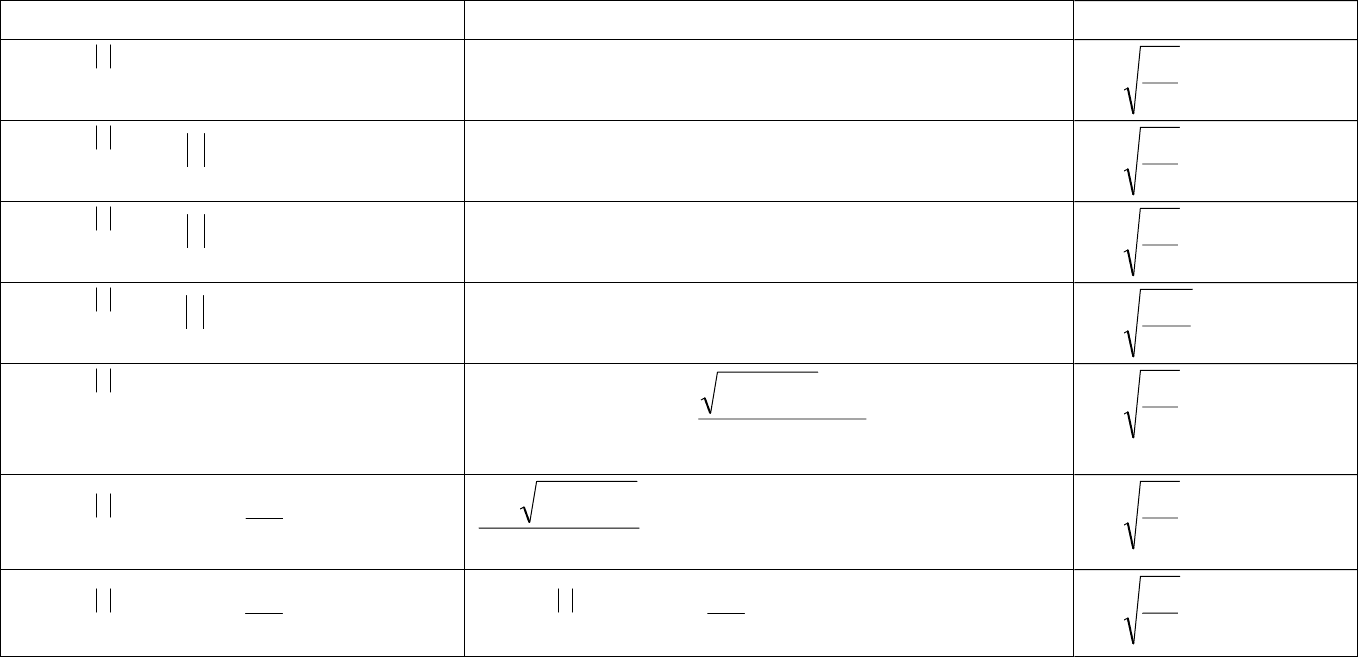
Приложение 12
Импульсные характеристики формирующих фильтров для генерирования псевдослучайных последовательностей с
заданным видом корреляционных функций методом нерекурсивной фильтрации
()
τ
x
K
(
)
τh
K
τα−
σ e
2
x
α
τ
−
α ek
απ
σ
1
x
(
)
τα+σ
τα−
1e
2
x
α
τ
−
τα ek
2
απ
σ
2
x
(
)
τα−σ
τα−
1e
2
x
(
)
ατ−α
α
τ
−
1ek
απ
σ
2
x
(
)
3/1e
222
x
τα+τα+σ
τα−
α
τ
−
τα ek
23
απ
σ
3
2
x
τωσ
τα−
0
2
x
cose
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
α−ω+α
+τωα
ατ−
0
0
2
0
2
0
sincosek
απ
σ
1
x
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
α
+τωσ
τα−
0
0
0
2
x
sincose
τω
ω
ω+αα
ατ−
0
0
2
0
2
sine
k
απ
σ
2
x
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
α
−τωσ
τα−
0
0
0
2
x
sincose
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
α
−τωα
τα−
0
0
0
sincosek
απ
σ
2
x
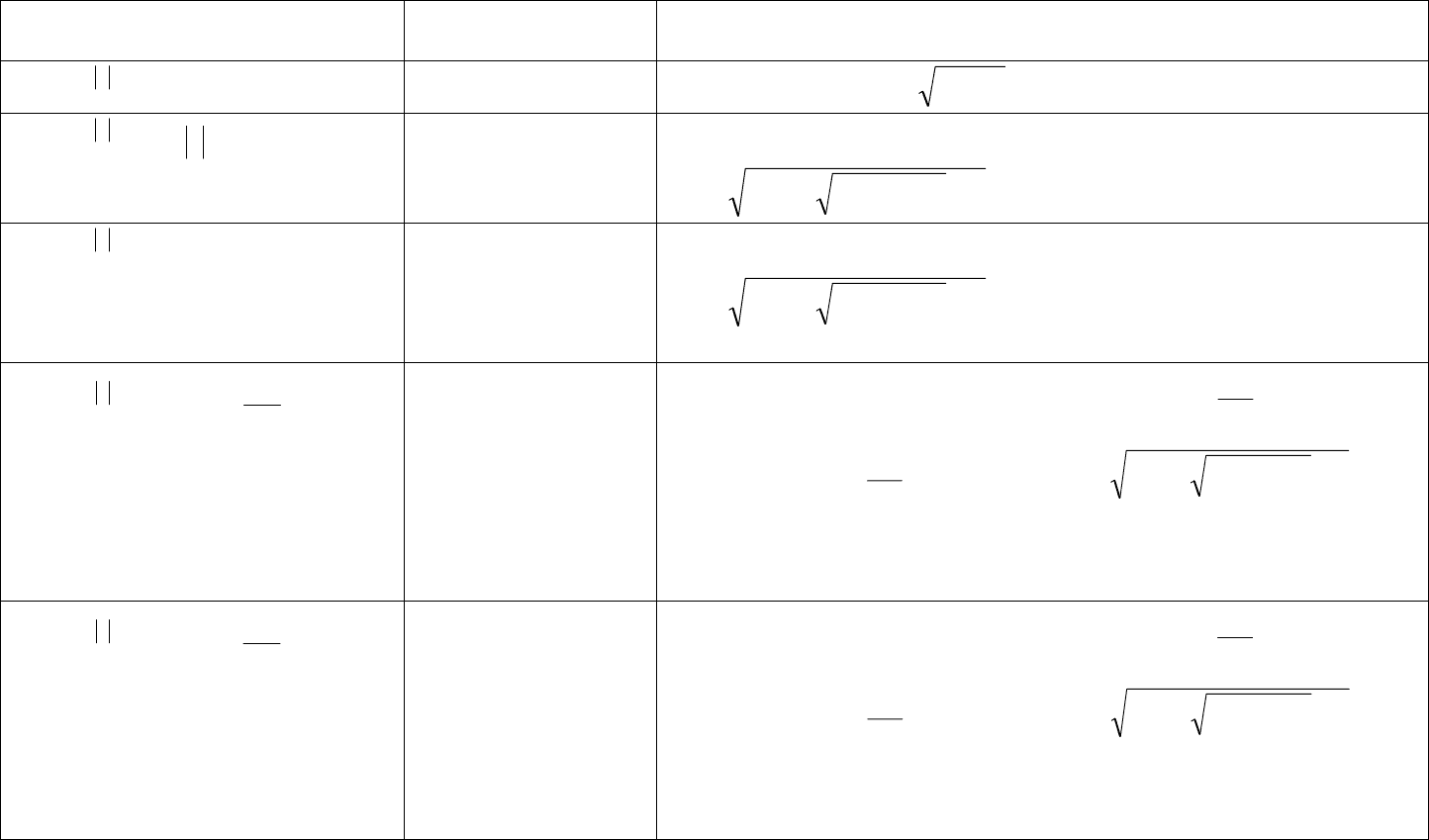
Приложение 13
Импульсные характеристики формирующих фильтров для генерирования псевдослучайных последовательностей с
заданным видом корреляционных функций методом рекурсивной фильтрации
Вид модели Моделирующий
алгоритм
Параметры алгоритма
τα−
σ e
2
x
1n1n0n
ybxay
−
+
=
pb;p1a;ep;t
1
2
0
=−==Δα=γ
γ−
()
τα+σ
τα−
1e
2
x
2n21n1
1n1n0n
ybyb
xaxay
−−
−
++
+
=
(
)
(
)
(
)
2
21101
2
0
2
1
2
10
42
1
3
0
pb;p2b;/a;2/4a
;pp41;1p1p;ep;t
−==αα=α−α±α=
−γ−=αγ−−γ+=α=Δα=γ
γ−
τωσ
τα−
0
2
x
cose
2n21n1
1n1n0n
ybyb
xaxay
−−
−
++
+
=
(
)
(
)
2
201101
2
0
2
1
2
10
4
10
2
000
pb;cosp2b;/a;2/4a
;p1;cos1pp;ep;t;t
−=γ=αα=α−α±α=
−=αγ−=α=Δω=γΔα=γ
γ−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
α
+τωσ
τα−
0
0
0
2
x
sincose
2n21n1
1n1n0n
ybyb
xaxay
−−
−
++
+
=
(
)
(
)
(
)
2
201101
2
0
2
1
2
1000
0
24
1
0
2
0
0
2
000
pb;cosp2b;/a
;2/4a;cossinp4p1
;sinpp1cos1pp;ep;t;t
−=γ=αα=
α−α±α=γγ
ω
α
−−=α
γ+
ω
α
+γ−=α=Δω=γΔα=γ
γ−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
α
−τωσ
τα−
0
0
0
2
x
sincose
2n21n1
1n1n0n
ybyb
xaxay
−−
−
++
+
=
(
)
(
)
(
)
2
201101
2
0
2
1
2
1000
0
24
1
0
2
0
0
2
000
pb;cosp2b;/a
;2/4a;cossinp4p1
;sinpp1cos1pp;ep;t;t
−=γ=αα=
α−α±α=γγ
ω
α
+−=α
γ+
ω
α
−γ−=α=Δω=γΔα=γ
γ−
204
Приложение 14
Параметрические модели корреляционных функций
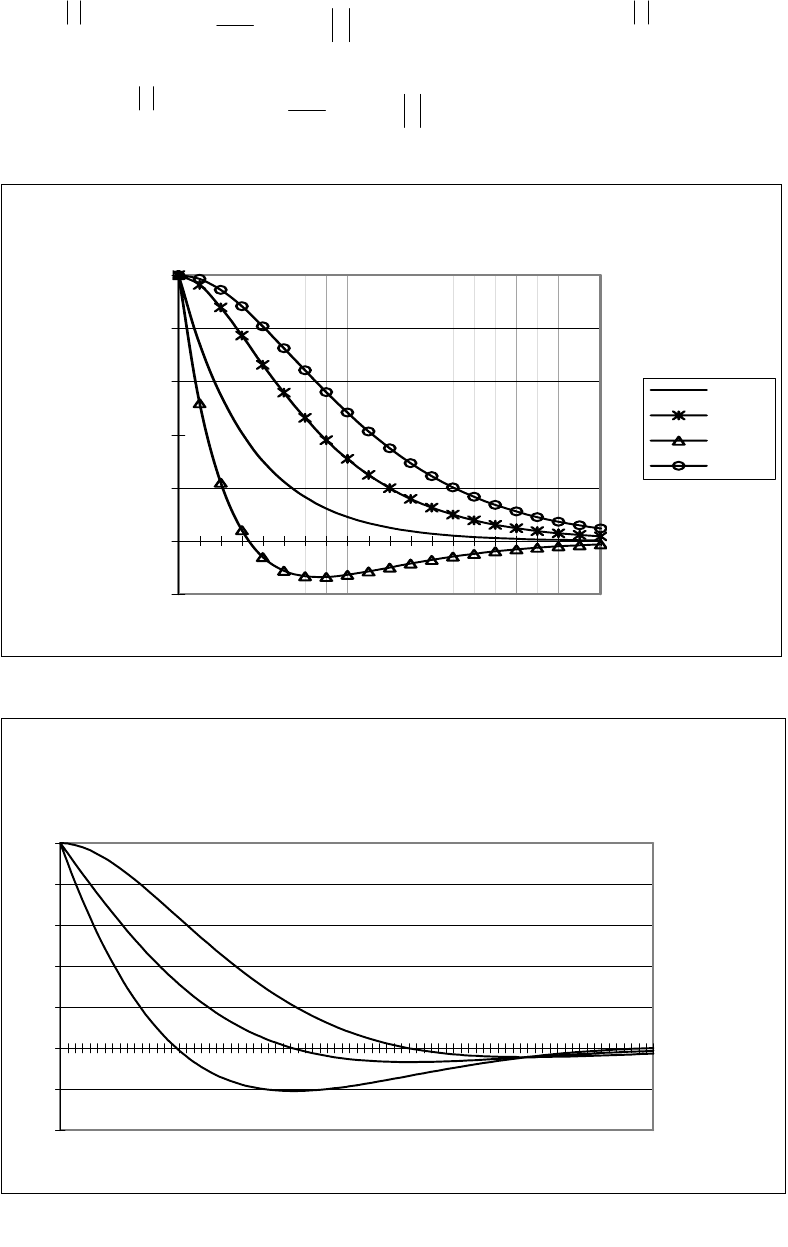
На рис. П.14.1 графики соответствуют (сверху вниз):
)(
4x
τ
ρ
(ряд1), )(
2x
τ
ρ
(ряд 2),
)(
1x
τρ (ряд 3), )(
3x
τρ (ряд 4).
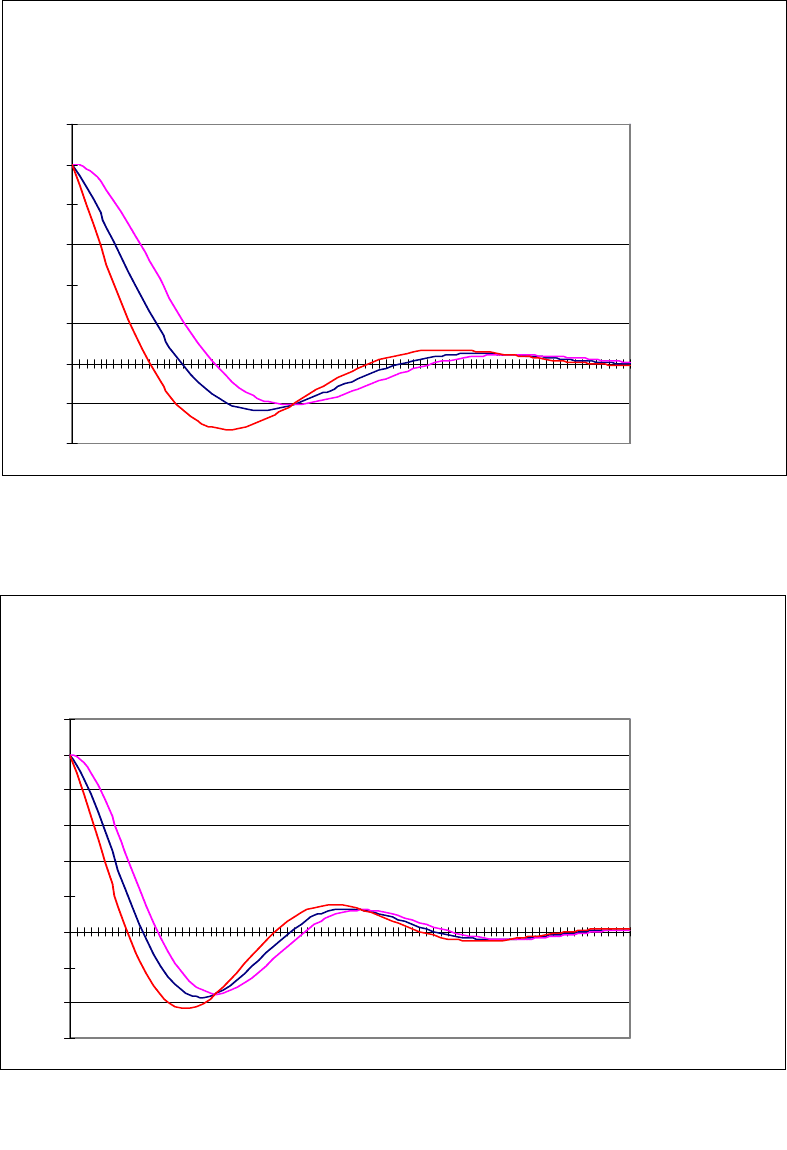
На рис. П.14.2 и далее верхняя кривая соответствует модели
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
λ
+τω=τρ
τλ−
0
0
0x6
sincose , средняя -
(
)
τω=τρ
τλ−
0x5
cose , нижняя –
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
λ
−τω=τρ
τλ−
0
0
0x7
sincose .
Однопараметрические модели КФ
-0,2
0
0,2
0,4
0,6
0,8
1
1
3
5
7
9
11
13
15
17
19
21
t
Ряд1
Ряд2
Ряд3
Ряд4
Рисунок П.14.1
Колебательные КФ
(показатель колебательности 1)
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
1 1019283746556473
t
Рисунок П.14.2
205
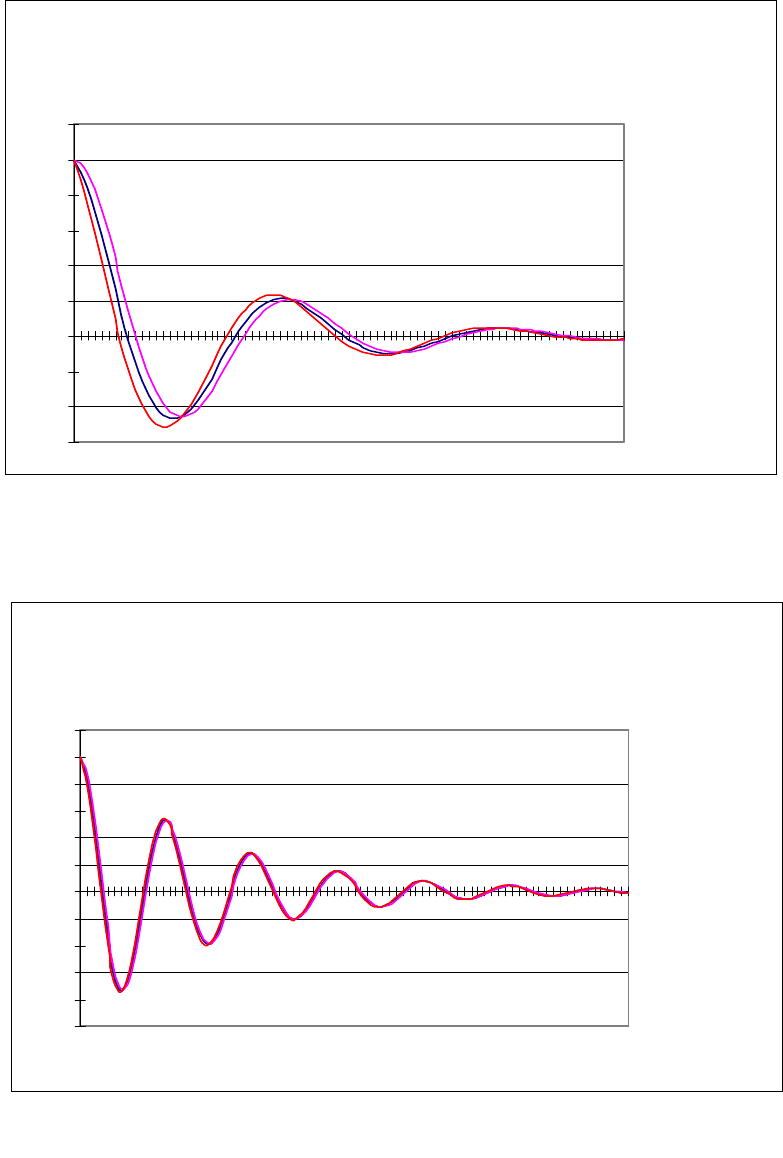
Колебательные КФ
(показатель колебательности 2)
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
1,2
1 6 11 16 21 26 31 36 41 46 51 56 61 66 71 76 81
Колебательные КФ
(показатель колебательности 3)
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
1,2
1 6 11 16 21 26 31 36 41 46 51 56 61 66 71 76 81
Рисунок П.14.4
Рисунок П.14.3
206
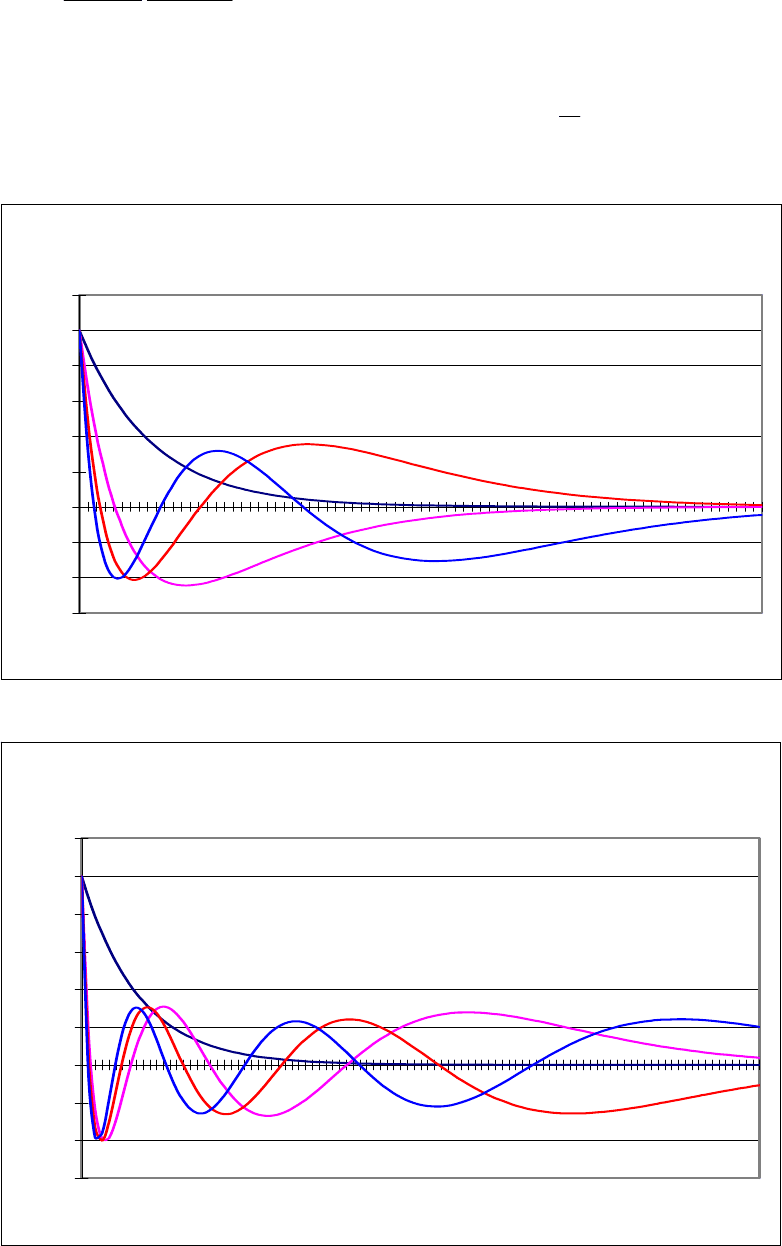
Колебательные КФ
(показатель колебательности 4)
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
1,2
1 6 11 16 21 26 31 36 41 46 51 56 61 66 71 76 81
Колебательные КФ
(показатель колебательности 10)
-1
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
1,2
1 6 11 16 21 26 31 36 41 46 51 56 61 66 71 76 81
t
Рисунок П.14.6
Рисунок П.14.5
207
Приложение 15
Ортогональные функции Лагерра
Ортогональные функции Лагерра, определяемые выражением
()
()
()
()
∑
=
ατ−
ατ−
−
=τ
k
0s
2/
2
s
k
e
!s
!sk
!k
L
,
удовлетворяют следующему свойству:
() ()
LLd
пиkn
пиkn
kn
τττ
α
=
≠
=
⎧
⎨
⎪
⎩
⎪
∞
∫
0
1
0
, р ;
, р .
Вид первых 6 ортогональных функций Лагерра приведен ниже.
Функции Лагерра 0, 1-3 порядков
-0 ,6
-0 ,4
-0 ,2
0
0,2
0,4
0,6
0,8
1
1,2
1 5 9 131721252933374145495357616569737781
t
Функции Лагерра 0, 4-6 порядков
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
1,2
1 8 15 22 29 36 43 50 57 64 71 78 85 92 99
t
Рисунок П.15.1
Рисунок П.15.2
208
Приложение 16
Интервалы корреляции для типовых моделей корреляционных функций
№ Наименование
τ
k
(2)
τ
k
(4)
1
τα−
e
1/α 1/2α
2
τα−
e (1+α|τ|)
2/α
5/4α
3
τα−
e (1−α|τ|)
0
α4
/
1
4
τα−
e (1+α|τ|+α
2
τ
2
/3)
α
3
/
8 α4
/
7
5
τα−
e Cosω
0
τ
α
αω
2
0
2
+
()
2
4
2
0
2
2
0
2
αω
αα ω
+
+
6
τα−
e (Cosω
0
τ+α/ω
0
Sinω
0
τ)
2
2
0
2
α
αω+
()
2
0
2
2
0
2
4
5
ω+αα
ω+α
7
τα−
e (Cosω
0
τ−α/ω
0
Sinω
0
τ)
0
α4
1
Приложение 17
Моменты для типовых моделей корреляционных функций
№ Наименование
1
μ
2
μ
3
μ
1
τα−
e
1/α
2
2/α
3
6/α
4
2
τα−
e (1+α|τ|)
3/α
2
8/α
3
30/α
4
3
τα−
e (1−α|τ|)
−1/α
2
-4/α
3
−18/α
4
4
τα−
e (1+α|τ|+α
2
τ
2
/3)
2
/
5
α
3
/
16
α
4
/
70 α
5
τα−
e Cosω
0
τ
()
2
2
0
2
2
0
2
ω+α
ω−α
(
)
()
3
2
0
2
2
0
3
32
ω+α
αω−α
()
4
2
0
2
4
0
2
0
24
6
6
ω+α
ω+ωα−α
6
τα−
e (Cosω
0
τ+α/ω
0
Sinω
0
τ)
()
2
2
0
2
2
0
2
3
ω+α
ω−α
(
)
()
3
2
0
2
2
0
2
8
ω+α
ω−αα
()
4
2
0
2
4
0
2
0
24
105
6
ω+α
ω+ωα−α
7
τα−
e (Cosω
0
τ−α/ω
0
Sinω
0
τ)
()
2
2
0
2
1
ω+α
()
2
2
0
2
4
ω+α
α
−
()
4
2
0
2
4
0
2
0
24
23
6
ω+α
ω−ωα+α
−
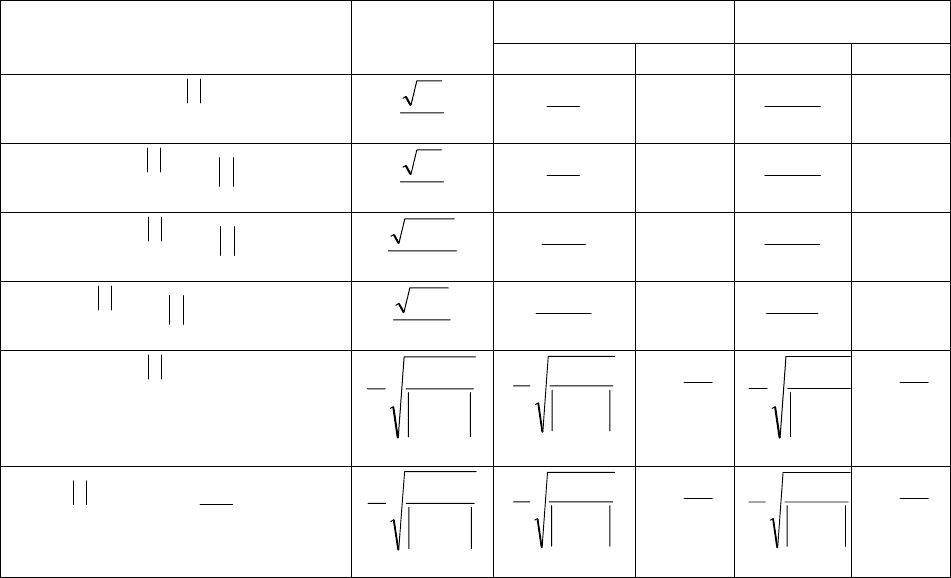
209
Приложение 18
Количество ординат корреляционной функции и интервалы дискретизации
()
ρτδ
x
\
t
Δ
02,0
=
δ
05,0=δ
t
Δ
Jmax
t
Δ
Jmax
τα−
e
α
δ8
α
4,0
9
α
632,0
6
()
τα+
τα−
1e
α
δ8
α
4,0
13
α
632,0
9
()
τα−
τα−
1e
α
δ 3/8
α
23,0
19
α
365,0
13
(
)
3/1e
22
τα+τα+
τα−
α
δ24
α
693,0
10
α
095,1
7
τω
τα−
0
cose
1
81
2
−μ
δ
α
1
16,01
2
−μ
α
π
μ
2
47
1
4,01
2
−μ
α
π
μ
2
47
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
α
±τω
τα−
0
0
0
sincose
1
81
2
+μ
δ
α
1
16,01
2
+μ
α
π
μ
2
47
1
4,01
2
+μ
α
π
μ
2
47
