Прохоров С.А. Лабораторный практикум. Моделирование и анализ случайных процессов
Подождите немного. Документ загружается.

90
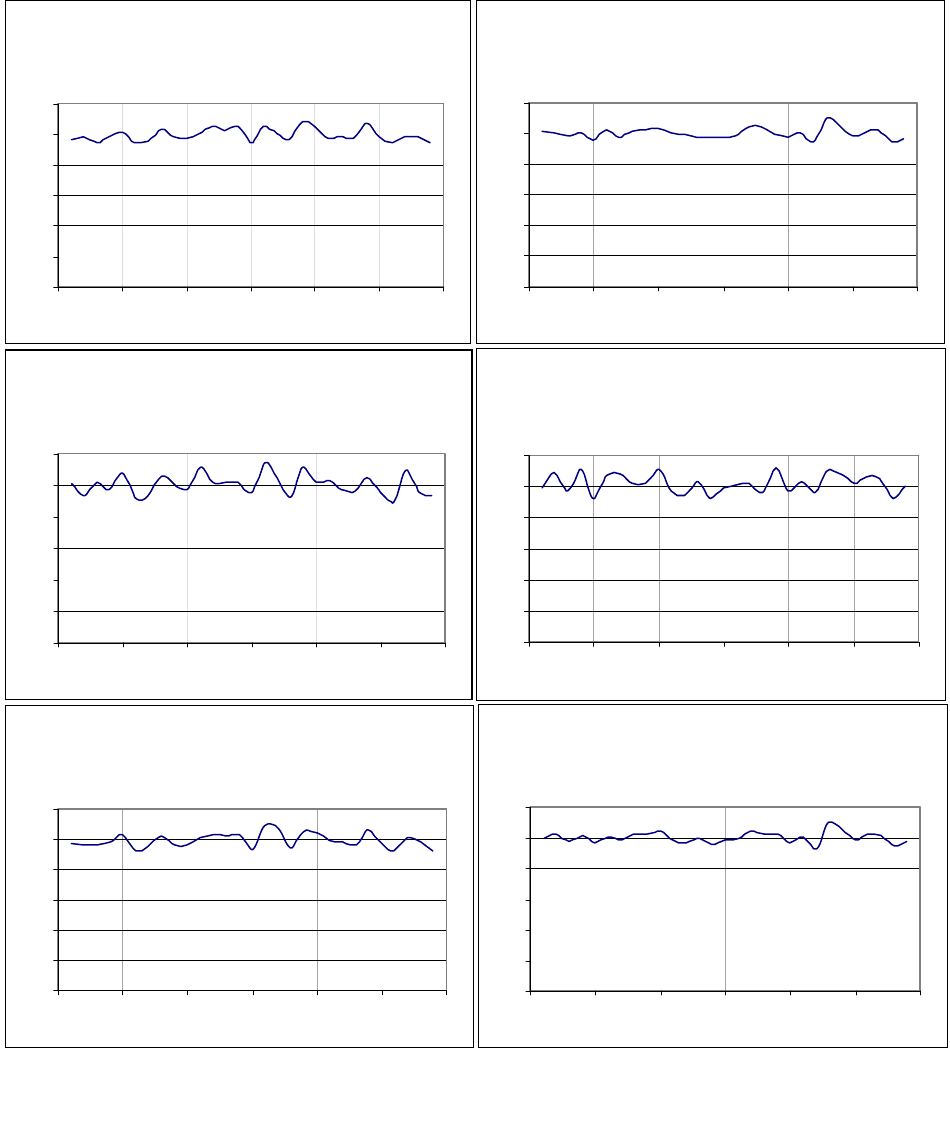
Ниже приведены результаты оценки параметра закона распределения различ-
ными аппроксимативными методами.
Параметр закона распред еления
(метод моментов)
0
0,2
0,4
0,6
0,8
1
1,2
0 5 10 15 20 25 30
Параметр закона распред еления
(аппроксимация плотности)
0
0,2
0,4
0,6
0,8
1
1,2
0 5 10 15 20 25 30
Параметр закона распред еления
(аппроксимация функции)
0
0,2
0,4
0,6
0,8
1
1,2
0 5 10 15 20 25 30
N=500, M=10
Параметр закона распреде ления
(метод моментов)
0
0,2
0,4
0,6
0,8
1
1,2
0 5 10 15 20 25 30
Параметр закона распреде ления
(аппроксимация функции)
0
0,2
0,4
0,6
0,8
1
1,2
0 5 10 15 20 25 30
N=500, M=18
Рисунок 5.3. Результаты моделирования
Параметр закона распреде ления
(аппроксимация плотности
)
0
0,2
0,4
0,6
0,8
1
1,2
0 5 10 15 20 25 30
91
5.4. Контрольные вопросы
1. Какие численные методы применяются при аппроксимации законов распре-
деления?
2. Из каких соображений выбирается начальное приближение?
3. Какой из методов аппроксимации обладает лучшей сходимостью?
4. Какой из методов аппроксимации более трудоёмкий?
Параметр закона распред еления
(метод моментов)
0
0,2
0,4
0,6
0,8
1
1,2
0 5 10 15 20 25 30
Параметр закона распред еления
(аппроксимация плотности)
0
0,2
0,4
0,6
0,8
1
1,2
0 5 10 15 20 25 30
Параметр закона распред еления
(аппроксимация функции)
0
0,2
0,4
0,6
0,8
1
1,2
0 5 10 15 20 25 30
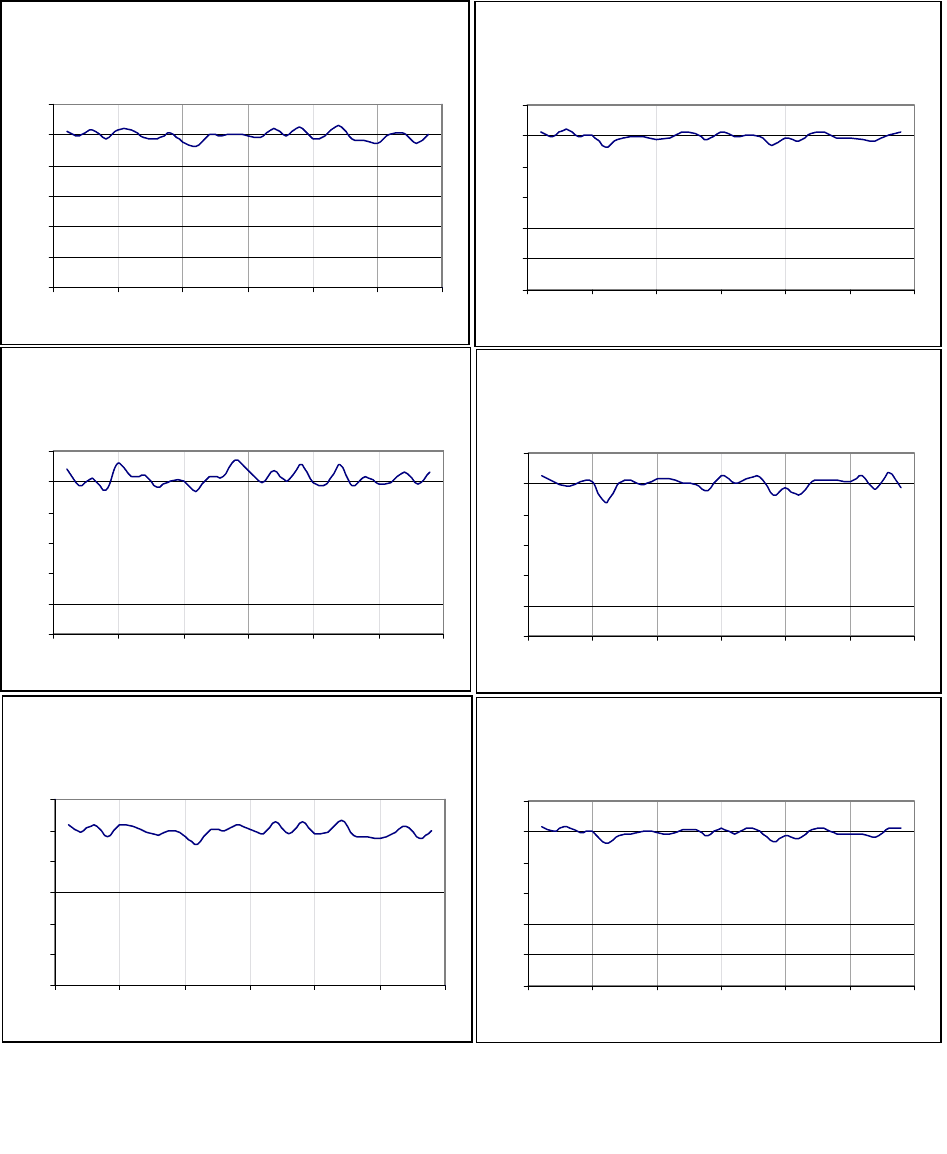
N=1000, M=10
Параметр закона распред еления
(метод моментов)
0
0,2
0,4
0,6
0,8
1
1,2
0 5 10 15 20 25 30
Параметр закона распред еления
(аппроксимация плотности)
0
0,2
0,4
0,6
0,8
1
1,2
0 5 10 15 20 25 30
Параметр закона распред еления
(аппроксимация функции)
0
0,2
0,4
0,6
0,8
1
1,2
0 5 10 15 20 25 30
N=1000, M=18
Рисунок 5.4. Результаты моделирования
92
6. АППРОКСИМАЦИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И
СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ МОЩНОСТИ
ПАРАМЕТРИЧЕСКИМИ МОДЕЛЯМИ
Цель работы:
изучение методов и приобретение практических навыков при
аппроксимации корреляционных функций и спектральных
плотностей мощности случайных процессов.
6.1. Теоретические основы лабораторной работы
В решении этой задачи возникает необ-
ходимость при обработке результатов научных
исследований, комплексных испытаний с це-
лью построения аналитических моделей кор-
реляционных функций и спектральных плот-
ностей мощности случайных процессов.
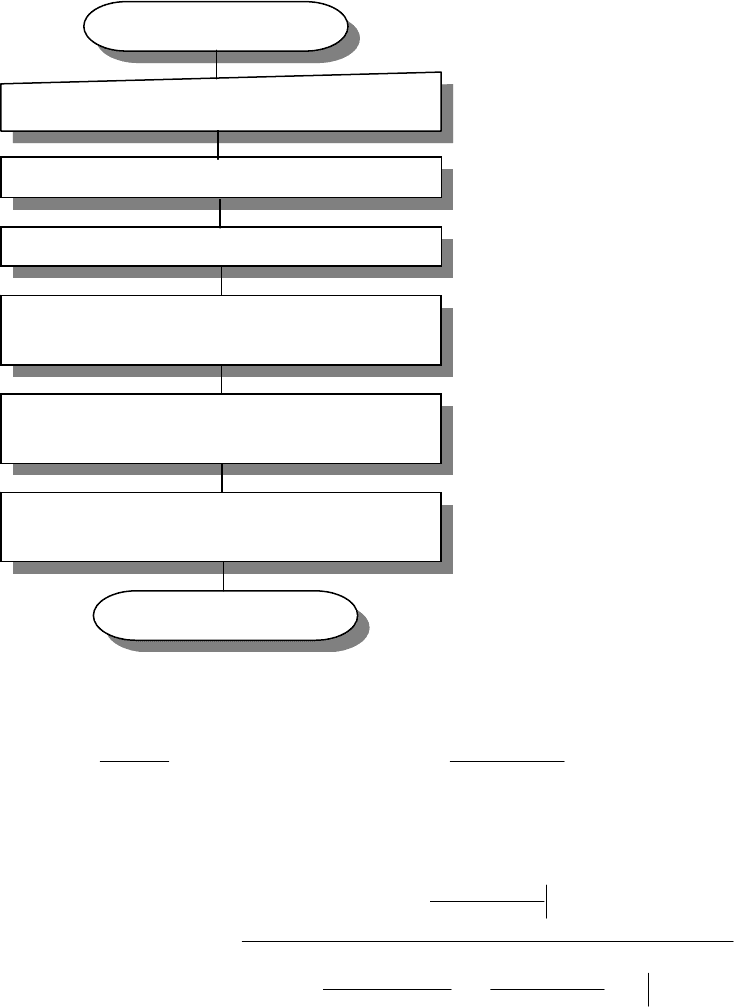
Блок-схема алгоритма аппроксимации
представлена на рис. 6.1.
С учетом того, что исходными данными,
подлежащими обработке, является массив зна-
чений ординат нормированной корреляцион-
ной функции -
(
)
{
}
maxJ,...0J
x
J
=
τ
Δ
ρ
, критерий
приближения целесообразнее записать в виде:
() ( )
[]
.min,
2
maxJ
0i
iaix
=ατρ−τρ=Δ
∑
=
(6.1)
В случае, если модель содержит один
параметр, задача сводится к решению одного
уравнения. Найдем это уравнение. Для этого
необходимо, подставив в (6.1)
()
α
τρ ,
ia
, вы-
полнить дифференцирование и результат при-
равнять нулю:
()
() ( )
[]
(
)
0
,
,
ia
maxJ
0i
iaix
=
∂α
ατ∂ρ
ατρ−τρ=
∂α
αΔ∂
∑
=
. (6.2)
Для решения полученного уравнения воспользуемся методом Ньютона [7-8].
Тогда
(
)
() ()
,
,,
R
,
R
N
0i
n
2
ia
2
ia
2
i
maxJ
0i
n
ia
i
n1n
∑
∑
=
=
+
α=α
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
∂α
ατ∂ρ
−
α∂
ατρ∂
α=α
∂α
ατ∂ρ
−α=α
(6.3)
где
() ( )
R
ixi ai
=−ρτ ρ
τ
α,.
Начало
Априорная информация о процессе
О
ц
енка о
рд
инат КФ
И
д
енти
ф
ика
ц
ия п
р
о
ц
есс
а
Выбор аппроксимирующего
вы
р
ажения
Аппроксимация КФ с оценкой погреш-
ности
Оценка корреляционных характеристик
по па
р
амет
р
ам модели
Коне
ц
Рис
у
нок 6.1. Алго
р
итм апп
р
оксимации

93
Начальное приближение
3
€
maxk
0
τ
=α (см. таблицу 3.2). Процесс вычисления
заканчивается, когда
α
α
ε
nn+
−≤
1
, где ε - любое малое наперёд заданное число.
Рассмотрим примеры решения задачи аппроксимации корреляционных функ-
ций типовыми однопараметрическими моделями.
Аналитическое выражение
()
ρτα
ατ
a
e
1
, =
−
широко применяется для аппрок-
симации корреляционных функций недифференцируемых широкополосных процес-
сов. Параметр модели определяется в результате решения следующего уравнения [7-
8]:
[]
∑
∑
=
τα−τα−
=
τα−
+
τ−τ
τ
−α=α
maxJ
1i
2
ii
2
2
i
maxJ
1i
ii
n1n
inin
in
eRe
eR
, (6.4)
где
()
in
eR
ix
^
i
τα−
−τρ= .
Следует подчеркнуть, что эта простая модель оказывается весьма полезной при
определении скорости затухания корреляционной функции, оценки максимального
интервала корреляции. Подобные задачи возникают при создании автоматизирован-
ных систем сбора и обработки информации, систем автоматического управления и
регулирования, систем передачи данных, когда приходится выбирать шаг дискрети-
зации во времени. Часто эта модель
выбирается в качестве базовой при оценке точно-
стных характеристик аппаратно-программных средств, так как существует большой
класс динамических систем, для которых случайные процессы с экспоненциальной
корреляционной функцией оказываются наихудшими с точки зрения помехозащи-
щенности.
Аналитическое выражение
()
(
)
ρτα ατ
ατ
a
e
2
1, =+
−
применяется для аппрок-
симации корреляционных функций однократно дифференцируемых широкополосных
случайных процессов. Параметр модели определяется в результате решения уравне-
ния [7-8]:
()
[]
∑
∑
=
τα−
=
τα−
+
τα−−τατ
τα
−α=α
maxJ
1i
2
i
2
nini
2
i
maxJ
1i
2
ini
n1n
1Re
eR
in
in
, (6.5)
где
() ( )
ini
x
^
i
1eR
in
τα+−τρ=
τα−
.
Аналитическое выражение
()
(
)
ρτ ατ
ατ
a
e
3
1=−
−
применяется для аппрок-
симации корреляционных функций недифференцируемых широкополосных процес-
сов, у которых
()
S
x
00
=
. Параметр определяется в результате решения уравнения [7-
8]:

94
()
() ()
[]
∑
∑
=
τα−τα−
=
τα−
+
−τατ−τα−τ
−τατ
−α=α
maxJ
1i
in
2
2
iin
2
ii
maxJ
1i
inii
n1n
1e2eR
1eR
inin
in
, (6.6)
где
() ( )
Re
ixi ni
ni
=− −
−
ρτ ατ
ατ
^
.1
Аналитическое выражение
(
)
τω=ωατρ
τα−
004a
cose,, применяется при ап-
проксимации корреляционных функций недифференцируемых узкополосных процес-
сов. Параметры модели определяются в результате решения системы двух трансцен-
дентных уравнений методом Ньютона [7-8]:
αα
ωω
nn
nn
SS S S
SS S
SS SS
SS S
+
+
=−
−
−
=−
−
−
⎧
⎨
⎪
⎪
⎩
⎪
⎪
1
15 24
35 4
2
1
23 14
35 4
2
;
,
(6.7)
где
(
)
;A
€
R;sinAA;cosAA;eA
2ixiin13in121
in
−τρ=τω=τω==
τα−
() ()
∑∑∑ ∑
=== =
−τ=−τ=τ=τ=
maxJ
0i
maxJ
0i
maxJ
0i
maxJ
0i
i23
2
i4i22
2
i3i3i2i2i1
;RAAS;RAAS;ARS;ARS
()
∑
=
+τ=
maxJ
0i
2i
2
3
2
i5
ARAS .
Начальные значения α и ω
0
выбираются следующим образом (см. таблицу 2.2):
α
τ
ω
π
τ
0
0
3
2
=
=
′
⎧
⎨
⎪
⎪
⎩
⎪
⎪
kmax
;
,
(6.8)
где
′
τ
- интервал времени, соответствующий первому пересечению
()
ρτ
^
x
оси абс-
цисс.
Процесс вычисления заканчивается при совместном выполнении условий:
ωωε
ααε
nn
nn
+
+
−≤
−≤
⎧
⎨
⎩
1
1
;
.
(6.9)
При аппроксимации корреляционных функций дифференцируемых узкополос-
ных процессов применяется аналитическое выражение
()
ρταω ωτ
α
ω
ωτ
ατ
a
e
50 0
0
0
,, cos sin .=+
⎛
⎝
⎜
⎞
⎠
⎟
−
Система уравнений для определения параметров модели имеет вид (6.7).
Для рассматриваемого случая [7-8]
()
;
A
AR;sinAA;cosAA;eA
n
3n
2i
x
^
iin13in121
in
ω
α
−−τρ=τω=τω==
τα−

95
() (
(
)
;)/A/ARS);/1(AARS
maxJ
0i
maxJ
0i
nni2
2
nni3i2nin3i2i1
∑∑
==
ωατ−ωα−τ=ω−τα+τ=
(()()()())
;A/2AR/1AAS
maxJ
0i
i2nin3ii
2
nin3i23
∑
=
τ+ω+τατ−ω−τα+τ= (6.10)
()()
(
)
(
)
() ()
()()
;
/1A/1AR
/A/A/1AA
S
maxJ
0i
2
i
2
nin3nini2i
nni2
2
nni3nin3i2
4
∑
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τ+ω−τα−ω−τατ+
+ωατ−ωα−τω−τα+τ
=
()()
(
)
(
)
∑
=
⎟
⎠
⎞
⎜
⎝
⎛
ωαω+τ+τ+ωατ−ωα−τ=
maxJ
0i
nn
2
n
2
i3
2
i2i
2
nni2
2
nni35
//1AAR/A/AS .
При аппроксимации корреляционных функций недифференцируемых узкопо-
лосных случайных процессов, у которых
(
)
00S
x
=
, применяют выражение
()
ρταω ωτ
α
ω
ωτ
ατ
a
e
60 0
0
0
,, cos sin .=−
⎛
⎝
⎜
⎞
⎠
⎟
−
Система уравнений для определения параметров модели имеет тот же вид –
(6.7). В этом случае [7-8]
()
Ae A A AA R A
A
ni
ni ni i x i
n
n
121 31 2
3
== = =−+
−α τ
ωτ ωτ ρ τ
α
ω
;cos;sin; ;
^
()()
(
)
(
)
∑∑
==
ωα−τ+ωτα=ωτα−+τ=
maxJ
0i
maxJ
0i
3
2
nninin2i2nin3i2i1
A//ARS;/1AARS ;
()()()()
()
∑
=
ωτα−+ττ−ωτα−+τ=
maxJ
0i
nin3i2ii
2
nin3i23
/2AAR/1AAS ; (6.11)
()()
(
)
(
)
() ()
()()
∑
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ωτα−+τ−ωτα−τ+
+ωα−τ+ωταωτα−+τ
=
maxJ
0i
2
nin
2
i3nini2i
3
2
nninin2nin3i2
4
/1A/1A
A//A/1AA
S
;
()()
(
)
()
∑
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ωα−ττ+
+ωατ−ω
+ωα−τ+ωτα=
maxJ
0i
2
nnii2
nn
2
i
2
n3
i
2
3
2
nninin25
/2A
//1A
RA//AS
.
Начальные значения параметров модели и условия окончания вычислений ана-
логичны предыдущему случаю.
Следует отметить, что система уравнений с использованием метода Ньютона с
аналитическим взятием первой и второй производных имеет достаточно сложный
вид, обладает плохой сходимостью, решение сильно зависит от начального прибли-
жения. Одним из способов устранения ряда недостатков является применение
конеч-
но-разностного метода Ньютона [7-8].
Рассмотрим примеры решения задачи аппроксимации корреляционных функ-
ций типовыми однопараметрическими моделями с использованием конечно-
разностного метода Ньютона [7-8].
1.
()
τα−
=ατρ e,
1a
.
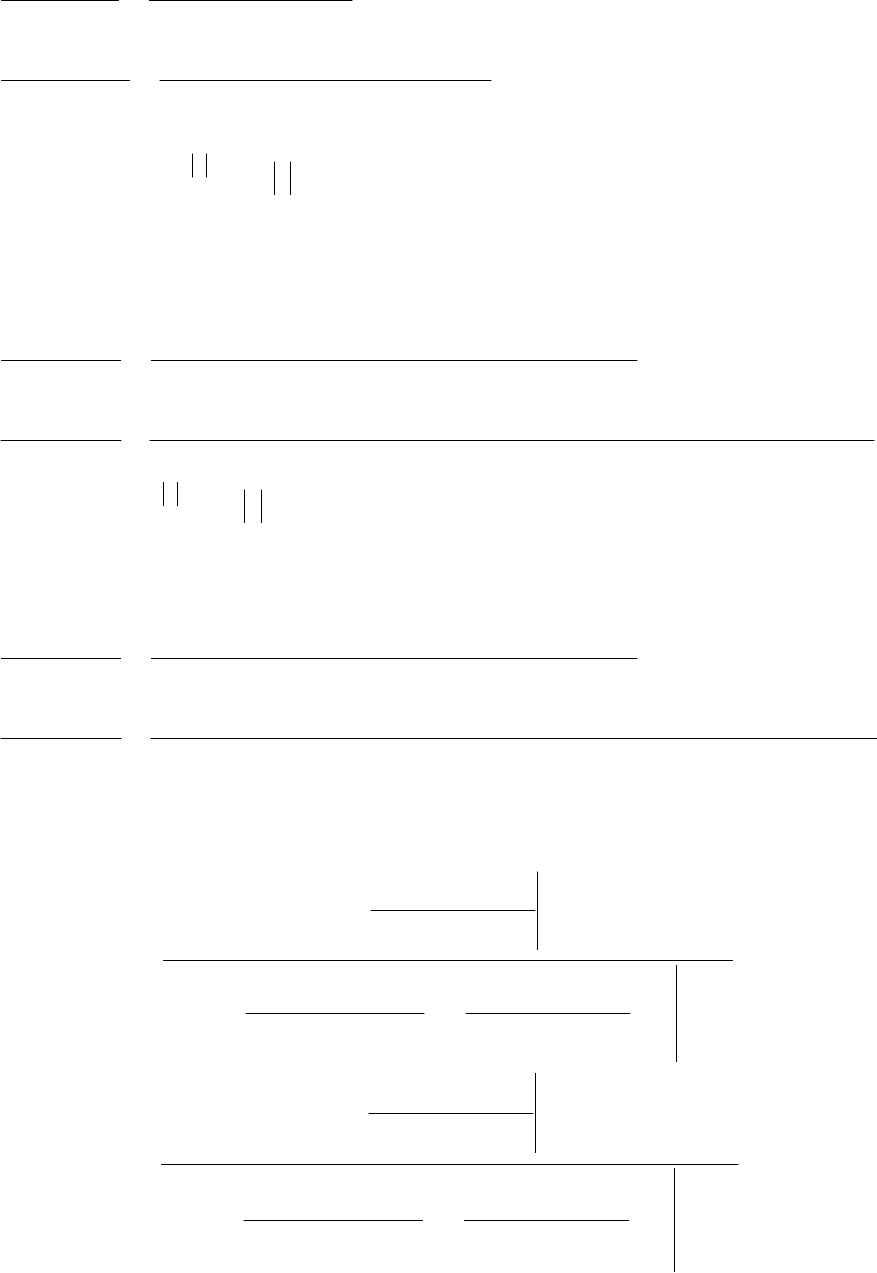
Параметр модели определяется в результате решения уравнения (6.7), где
()
in
i
x
^
i
eR
τα−
−τρ= ;
96
()
(
)
h
ee
,
inihn
ia
τ
α
−τ+α
−
−
≈
α∂
ατρ∂
;
()
(
)
(
)
2
ihninihan
2
ia
2
h
ee2e
,
τ−α−τατ+−
+−
≈
α∂
ατρ∂
,
где h – любое достаточно малое приращение по α.
2.
()
()
τα+=ατρ
τα−
1e,
2a
.
Параметр модели определяется в результате решения уравнения (6.7), в кото-
ром:
() ( )
in
in
i
x
^
i
1eR τα+−τρ=
τα−
;
()
(
)
(
)()
(
)
h
1eh1e
,
in
in
in
ihn
ia
τα+−τ+α+
≈
α∂
ατρ∂
τ
α
−
τ+α
−
;
()
(
)
()()
(
)
(
)
()()
2
in
ihn
in
in
in
ihan
2
ia
2
h
h1e1e2h1e
,
τ−α++τα+−τ+α+
≈
α∂
ατρ∂
τ−α−τατ+−
;
3.
()
()
τα−=τρ
τα−
1e
3a
.
Параметр определяется в результате решения уравнения (6.7), где:
() ( )
in
in
i
x
^
i
1eR τα−−τρ=
τα−
;
()
(
)
(
)()
(
)
h
1eh1e
,
in
in
in
ihn
ia
τα−−τ+α−
≈
α∂
ατρ∂
τ
α
−
τ+α
−
;
()
(
)
()()
(
)
(
)
()()
2
in
ihn
in
in
in
ihan
2
ia
2
h
h1e1e2h1e
,
τ−α−+τα−−τ+α−
≈
α∂
ατρ∂
τ−α−τατ+−
.
Для двухпараметрических моделей корреляционных функций параметры моде-
ли определяются в результате решения системы двух трансцендентных уравнений
методом Ньютона:
(
)
()()
()
()()
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω∂
ωατρ∂
−
ω∂
ωατρ∂
ω∂
ωατρ∂
−ω=ω
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
α∂
ωατρ∂
−
α∂
ωατρ∂
α∂
ωατρ∂
−α=α
ω=ω
=
αα
ω=ω
=
α
+
α=α
=
αα
α=α
=
α
+
∑
∑
∑
∑
.
,,,,
R
,,
R
;
,,,,
R
,,
R
n0
n0
n
n
N
0i
2
0
0i
2
0
0i
2
i
N
0i
0
0i
i
n1n
N
0i
2
0i
2
0i
2
i
N
0i
0i
i
n1n
(6.12)
Рассмотрим примеры решения задачи аппроксимации корреляционных функ-
ций типовыми двухпараметрическими моделями с использованием конечно-
разностного метода Ньютона [7-8].
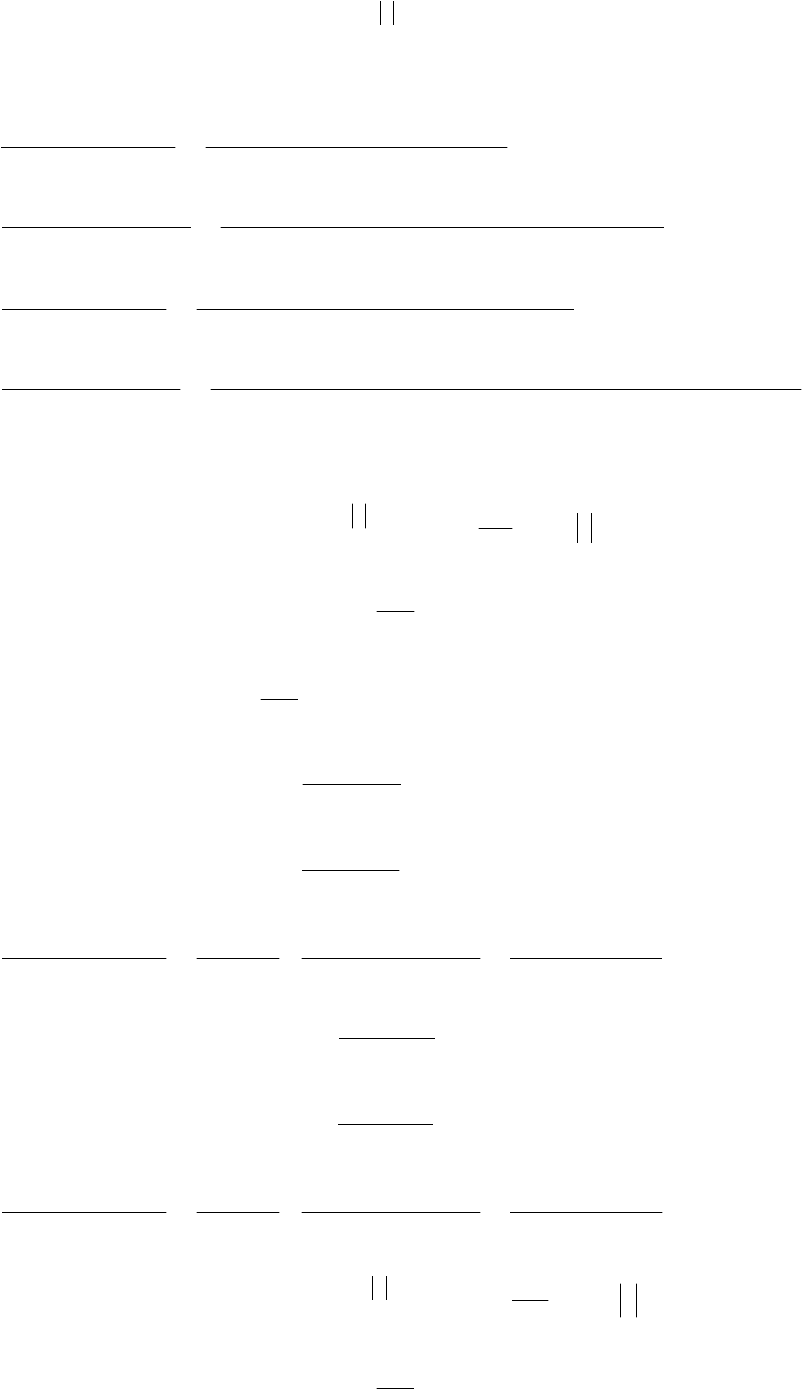
97
4. Для модели
()
τω=ωατρ
τα−
004a
cose,,
()
in
in
i
x
^
i
coseR τω−τρ=
τα−
;
()
(
)
(
)
h
eecos
,,
ianihan
in
0ia
τ−τ+−
−τω
≈
α∂
ωατρ∂
;
()
(
)
(
)
(
)
2
ihanianihan
in
2
0ia
2
h
ee2ecos
,,
τ−−τ−τ+−
+−τω
≈
α∂
ωατρ∂
;
()
(
)
(
)()
k
coskcose
,,
inin
ian
0ia
τω−τ+ω
≈
α∂
ωατρ∂
τ−
;
()
(
)
(
)()()()
2
ininin
ian
2
0ia
2
k
kcoscos2kcose
,,
τ−ω+τω−τ+ω
≈
α∂
ωατρ∂
τ−
,
где h – любое достаточно малое приращение по α,
k – любое достаточно малое приращение по ω
0
.
5. Для модели
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
α
+τω=ωατρ
τα−
0
0
005a
sincose,,
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
α
+τω−τρ=
τα−
in
n
n
in
in
i
x
^
i
sincoseR ;
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
α
+τω=
τα−
in
n
n
in
in
1
sincoseS
;
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
+α
+τω=
τ+α−
in
n
n
in
i)hn(
2
sin
)h(
coseS ;
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
−α
+τω=
τ−α−
in
n
n
in
i)hn(
3
sin
)h(
coseS ;
()
h
SS
,,
12
0ia
−
≈
α∂
ωατρ∂
;
(
)
2
312
2
0ia
2
h
SS2S,, +−
≈
α
∂
ωατρ∂
;
()()
()
()()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τ+ω
+ω
α
+τ+ω=
τα−
in
n
n
in
in
4
ksin
k
kcoseS ;
()()
()
()()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τ−ω
−ω
α
+τ−ω=
τα−
in
n
n
in
in
5
ksin
k
kcoseS ;
()
k
SS
,,
14
0
0ia
−
≈
ω∂
ωατρ∂
;
(
)
2
514
2
0
0ia
2
k
SS2S,, +−
≈
ω∂
ωατρ∂
.
6. Для модели
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
α
−τω=ωατρ
τα−
0
0
005a
sincose,,
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
α
−τω−τρ=
τα−
in
n
n
in
in
i
x
^
i
sincoseR ;
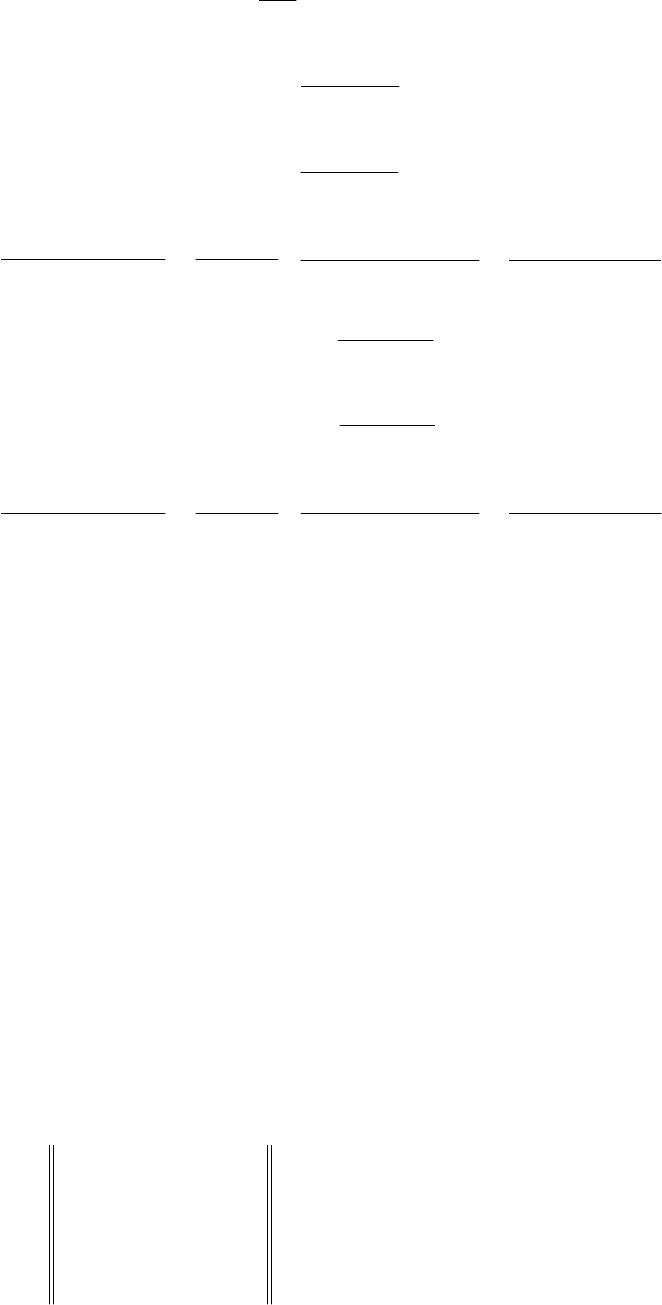
98
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
α
−τω=
τα−
in
n
n
in
in
1
sincoseS ;
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
+α
−τω=
τ+α−
in
n
n
in
i)hn(
2
sin
)h(
coseS ;
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τω
ω
−α
−τω=
τ−α−
in
n
n
in
i)hn(
3
sin
)h(
coseS ;
()
h
SS
,,
12
0ia
−
≈
α∂
ωατρ∂
;
(
)
2
312
2
0ia
2
h
SS2S,, +−
≈
α
∂
ωατρ∂
;
()()
()
()()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τ+ω
+ω
α
−τ+ω=
τα−
in
n
n
in
in
4
ksin
k
kcoseS ;
()()
()
()()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τ−ω
−ω
α
−τ−ω=
τα−
in
n
n
in
in
5
ksin
k
kcoseS ;
()
k
SS
,,
14
0
0ia
−
≈
ω∂
ωατρ∂
;
(
)
2
514
2
0
0ia
2
k
SS2S,, +−
≈
ω∂
ωατρ∂
.
Начальные значения параметров модели и условия окончания вычислений оп-
ределяются по формулам (6.8) и (6.9).
При аппроксимации КФ функциями заданного вида можно также использовать
метод деформированного многогранника, который является одним из прямых мето-
дов многомерного поиска и выделяется высокой эффективностью и помехозащищен-
ностью [7-8].
Метод деформируемого многогранника Нелдера и Мида легко адаптируется к
особенностям оптимизируемой функции, «не замечает» отдельные шероховатости
функции (вызванные ошибками вычисления), а скорость сходимости алгоритма не
слишком сильно зависит от регулярности целевой функции. Очень часто этот метод
оптимизации конкурирует с такими мощными методами оптимизации, как метод
Ньютона.
Метод деформируемого многогранника является модификацией симплексного
метода. Симплексом называют регулярный многогранник в
n-мерном евклидовом
пространстве. Для случая 2-х переменных симплекс представляет собой равносторон-
ний треугольник; 3-х переменных - тетраэдр и т.д. Для
n-мерного пространства сим-
плекс всегда имеет
n+1 вершину.
Координаты вершин регулярного симплекса можно определить с помощью
матрицы размером
()
1nn +
×
:
122
212
221
r...rr0
...............
r...rr0
r...rr0
R =
, (6.13)
где
99
(
)
[
]
( )
()
[]
( )
,11n2nsr
,1n1n2nsr
2
1
−+=
−++=
(6.14)
s
- параметр, отождествляемый с расстоянием между двумя вершинами.
Элемент
ij
r матрицы R равен i-ой координате j-ой вершины симплекса.
Поиск минимума функции симплексным методом ведётся следующим образом:
1. В каждой вершине симплекса вычисляется значение функции
()
ii
xfy = .
2. Определяется вершина с наибольшим (наихудшим) значением
()
xf .
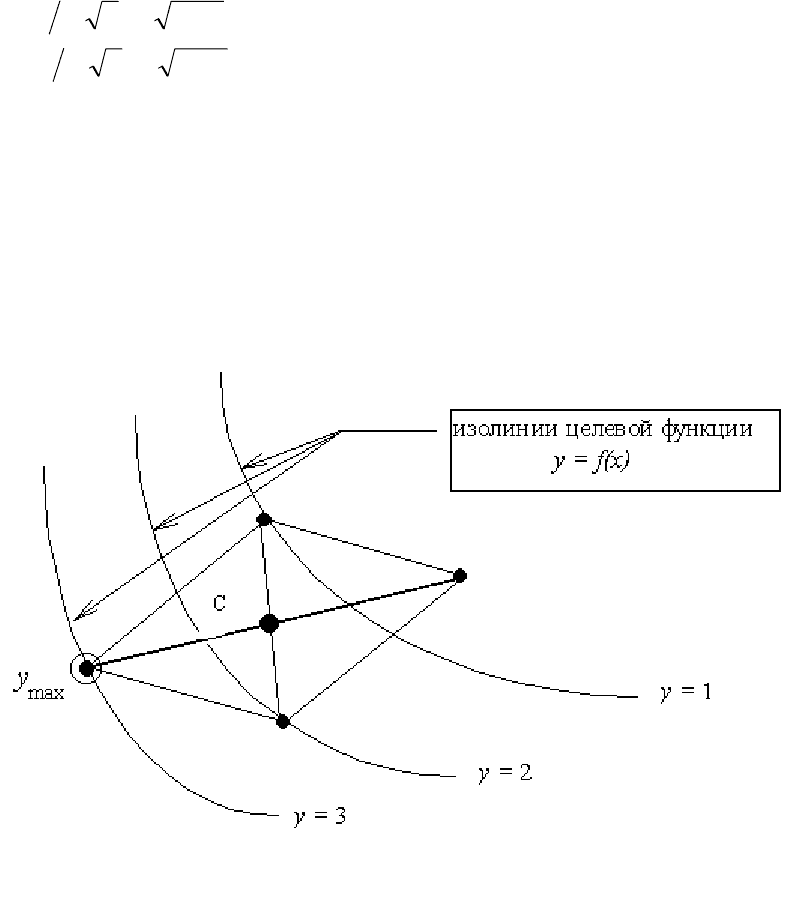
3. Через эту вершину и центральную точку симплекса проводится прямая, на
которой на некотором удалении от центра C устанавливается новая вершина (см. рис.
6.2).
4. Вершина с наибольшим значением
(
)
xF удаляется. Симплекс по существу
«переворачивается» через грань, противоположную наихудшей вершине.
5. Далее процесс повторяется, начиная с п.1.
Важной особенностью симплексного метода поиска является то, что для реали-
зации каждого последующего шага итерации необходимо вычислить функцию
(
)
xf
лишь в одной новой точке симплекса. Сама же оптимизация этим алгоритмом ассо-
циируется с процессом «кантования» симплекса вниз по поверхности функции
(
)
xf
в
направлении её минимума.
Регулярный метод симплексного поиска склонен к зацикливанию, поэтому,
Нелдер и Мид, нарушив регулярность, устранили указанный недостаток.
Обозначим
A
k
X - вершину многогранника (первоначального симплекса), кото-
рая даёт максимальное значение
(
)
xf
на k-ом шаге, а
B
k
X
- минимальную оценку
функции
()
xf . Определим вектор координат
C
k
X центра многогранника по следующей
формуле:
Рисунок 6.2. Геометрическая интерпретация симплексного поиска
