Пример решения задач по гидравлике на Маткаде
Подождите немного. Документ загружается.

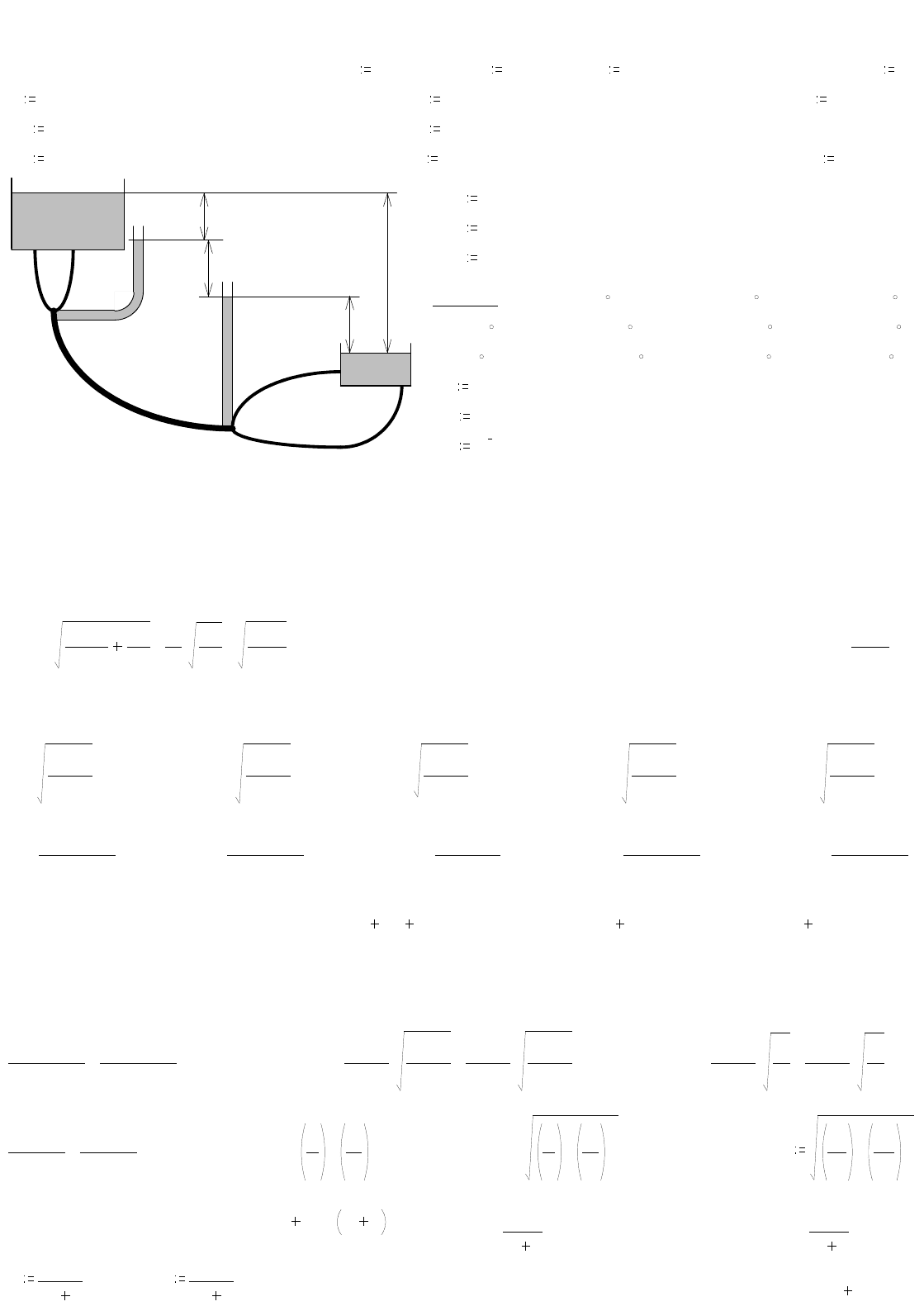
Задача № 26.
Определить расход воды V, перетекающий из верхнего резервуара в нижний при разности уровней H=... м.
Диаметры труб: d
1
=d
2
=... м; d
3
=... м; d
4
=... м; d
5
=... м; Длины труб: l
1
=l
2
=... м; l
3
=... м; l
4
=... м; l
5
=... м.
Местными потерями напора пренебречь.
л/с 0.001 мм 0.001 м 1
Номер варианта v:
v 2
H 6 7 8 10 10 10 8 7 6 7( )
0 v
0.25
d
1
2 3 2 4 4 3 2 2 3 4( )
0 v
0.05
d
2
d
1
d
3
3 4 3 2 3 2 4 3 2 3( )
0 v
0.05
d
4
3 3 2 5 2 3 2 5 2 3( )
0 v
0.025
d
5
3 3 2 5 3 2 3 3 3 3( )
0 v
0.025
l
1
4 6.2 .5 4 3.5 2 2.5 4 5 3.5( )
0 v
l
2
l
1
пьезометры
H
3
d
2
d
1
l
1
l
5
; d
5
l
4
; d
4
l
3
; d
3
l
2
H
H
4
=H
5
H
1
=H
2
l
3
3 3 3 3.5 2.5 1.5 1.5 3 1.75 2( )
0 v
l
4
2 2.5 2.5 3 2.5 3 3.5 2.5 3 2.5( )
0 v
l
5
4 5 5 8 8 8.5 6 4 5 4.5( )
0 v
Дано:
d
1
100 мм d
2
100 мм d
3
150 мм
d
4
50 мм d
5
50 мм l
1
0.5 м l
2
0.5 м
l
3
3 м l
4
2.5 м l
5
5 м H 2 м
g 9.807
м/с
2
— ускорение свободного падения.
1000
кг/м
3
— плотность воды.
10
6
м
2
/с — вязкость воды при t=20 °C.
Обозначим: H
1
=H
2
— потеря напора на первой и второй трубах (так как эти трубы соединены параллельно, то потери напора на
них должны быть равны), H
3
— потеря напора на третьей трубе; H
4
=H
5
— потеря напора на четвёртой и пятой трубах (эти трубы
соединены параллельно). V
1
— расход воды через первую трубу, V
2
— расход воды через вторую трубу. Очевидно, что
H=H
2
+H
3
+H
4
, V=V
1
+V
2
=V
4
+V
5
. Когда задан напор, а расход (или диаметр) неизвестен, то задача (в общем виде) решается
методом последовательных приближений. Коэффициент трения
будем вычислять по универсальной формуле Альтшулля. Так
как шероховатость труб
не задана, то считаем её равной нулю:
=0 (т. е. предполагаем, что режим течения турбулентный,
область гидравлически гладких труб (то есть число Рейнольдса Re лежит в пределах от 4000 до 10·d/
)).
= 0.1
4
1.46
d
100
Re
=
1
10
4
100
Re
=
4
d
400 V
где Re — число Рейнольдса – находится по формуле:
Re=
4 V
d
Составим систему из пятнадцатити уравнений с пятнадцатью неизвестными, пренебрегая местными потерями напора (на входе,
выходе, поворотах и в тройниках).
1
=
4
d
1
400 V
1
2
=
4
d
2
400 V
2
3
=
4
d
3
400 V
4
=
4
d
4
400 V
4
5
=
4
d
5
400 V
5
H
1
=
8 V
1
2
1
l
1
2
g
d
1
5
H
2
=
8 V
2
2
2
l
2
2
g
d
2
5
H
3
=
8 V
2
3
l
3
2
g
d
3
5
H
4
=
8 V
4
2
4
l
4
2
g
d
4
5
H
5
=
8 V
5
2
5
l
5
2
g
d
5
5
H
1
= H
2
H
4
= H
5
H =H
2
H
3
H
4
V= V
1
V
2
V= V
4
V
5
Эту систему можно решить аналитически: Возьмём двенадцатое уравнение (H
4
=H
5
) и выразим эти потери через соответствующие
расходы V
4
иV
5
из уравнений 9 и 10, подставив в них коэффициенты трения из уравнений 4 и 5 соответственно. Получим
уравнение, связывающее расходы V
4
иV
5
, т. е. найдём распределение общего расхода V между четвёртой и пятой трубами.
8 V
4
2
4
l
4
2
g
d
4
5
=
8 V
5
2
5
l
5
2
g
d
5
5
V
4
2
l
4
d
4
5
4
d
4
400 V
4
=
V
5
2
l
5
d
5
5
4
d
5
400 V
5
V
4
2
l
4
d
4
5
4
d
4
V
4
=
V
5
2
l
5
d
5
5
4
d
5
V
5
V
4
7
l
4
4
d
4
19
=
V
5
7
l
5
4
d
5
19
V
4
7
= V
5
7
l
5
l
4
4
d
4
d
5
19
V
4
= V
5
7
l
5
l
4
4
d
4
d
5
19
= k
2
V
5
k
2
7
l
5
l
4
4
d
4
d
5
19
k
2
1.485994289136948 V = V
4
V
5
= k
2
1 V
5
V
5
=
V
k
2
1
V
4
= k
2
V
5
=
k
2
V
k
2
1
= k'
V
k'
k
2
k
2
1
k''
1
k
2
1
k' 0.597746461297316 k'' 0.402253538702684 k' k'' 1
Аналогично найдём распределение общего расхода меж-
ду первой и второй трубами. Так как трубы одинаковые,
то расход между ними распределяется поровну: k
1
=1.
V
1
= k
1
V
2
= V
2
V = V
1
V
2
= k
1
1 V
2
= 2
V
2
V
2
=
V
2
Возьмём тринадцатое уравнение (H=H
2
+H
3
+H
4
) и подставим в его правую часть потери
H
2
,H
3
иH
4
, выраженные через расход V в третьей трубе. Получим уравнение для расхода V:
H = H
2
H
3
H
4
=
=
8 V
2
2
l
2
2
g
d
2
5
4
d
2
400V
2
8 V
2
l
3
2
g
d
3
5
4
d
3
400V
8 V
4
2
l
4
2
g
d
4
5
4
d
4
400V
4
=
4
4
2
g
5
V
2
2
l
2
d
2
5
4
d
2
V
2
V
2
l
3
d
3
5
4
d
3
V
V
4
2
l
4
d
4
5
4
d
4
V
4
=
=
4
4
V
2
2
g
5
4
V
l
2
4 d
2
5
4
2 d
2
l
3
d
3
5
4
d
3
k'
2
l
4
d
4
5
4
d
4
k'
= H
256
V
7
7
g
4
25
l
2
4 d
2
5
4
2 d
2
l
3
d
3
5
4
d
3
k'
2
l
4
d
4
5
4
d
4
k'
4
= H
4
V
7
=
H
4
7
g
4
25
256
l
2
4 d
2
5
4
2 d
2
l
3
d
3
5
4
d
3
k'
2
l
4
d
4
5
4
d
4
k'
4
V
7
H
4
7
g
4
25
256
l
2
4 d
2
5
4
2 d
2
l
3
d
3
5
4
d
3
k'
2
l
4
d
4
5
4
d
4
k'
4
V 0.025588 V 25.588 л/с
Ответ:
общий расход воды
V 25.6 л/с
Формулу для расхода V
можно ещё упростить:
V
2
7
12.5 H
4
g
4
l
2
4
2
4 d
2
4.75
l
3
d
3
4.75
k'
1.75
l
4
d
4
4.75
4
V 0.025588
Проверка:
V
1
0.5 V
V
1
12.794л/с V
4
k' V
V
4
0.015295
V
4
15.295л/с V
5
k'' V
V
5
0.010293 V
5
10.293л/с V
4
V
5
V 0 л/с
Re
3
4 V
d
3
Re
4
4 V
4
d
4
Re
5
4 V
5
d
5
Re
1
4 V
1
d
1
Re
3
217196 Re
4
389484 Re
5
262103 Re
1
162897
Режимы течения во всех трубах турбулентные, квадратичная зона (Re>> Re
кр
= 2320), как и предполагалось при решении задачи.
