Powers D.L. Boundary Value Problems and Partial Differential Equations

Подождите немного. Документ загружается.

288 Chapter 4 The Potential Equation

18. For the potential problem on an annular ring

∂

∂r



∂

∂r



∂

∂θ

=0, a < r < b,

show that product solutions have the form

ln(r), (C

θ)ln(r),



cos(nθ)+B

sin(nθ)



−n



cos(nθ)+D

sin(nθ)



19. Solve the potential problem on the annular ring as stated in Exercise 18

with boundary conditions

u(a,θ)=1, u(b,θ)= 0.

20. Find product solutions of the potential equation on a sector of a disk

with zero boundary conditions on the straight edges.

∇

u =0, 0 ≤r < c, 0 <θ <α,

u(r, 0) = 0, u(r,α)=0.

21. Solve the potential problem in a slit disk:

∇

u =0, 0 ≤r < c, 0 <θ<2π,

u(r, 0) = 0, u(r, 2π)= 0,

u(r,θ)= f (θ ), 0 <θ<2π.

22. Show that the function u(x, y) = sin(πx/a) sinh(π y /a) satisﬁes the po-

tential problem

∇

u =0, 0 < x < a, 0 < y,

u(0, y) = 0, u(a, y) = 0, 0 < y,

u(x, 0) = 0, 0 < x < a.

This solution is eliminated if it is also required that u(x, y) be bounded

as y →∞.

23. Solve the potential equation in the rectangle 0 < x < a,0< y < b, with

the boundary conditions

u(0, y) = 0,

∂u

∂x

(a, y) = 0, 0 < y < b,

u(x, 0) = 0, u(x, b) = x, 0 < x < a.

Miscellaneous Exercises 289

24. Find a polynomial of second degree in x and y,

v(x, y) = A +Bx +Cy +Dx

+Exy +Fy

that satisﬁes the potential equation and these boundary conditions:

v(0, y) =0, 0 < y < b,

v(x, 0) = 0,v(x, b) = x, 0 < x < a.

25. Find the problem (partial differential equation and boundary condi-

tions) satisﬁed by w(x, y) = v(x, y) − u(x, y),whereu and v are the so-

lutions of the problems in Exercises 23 and 24. Solve the problem. Is this

problem easier to solve than the one in Exercise 23?

26. Solve the potential equation in the quarter-plane 0 < x,0< y,subjectto

the boundary conditions

u(x, 0) = f (x), 0 < x,

u(0, y) = f (y), 0 < y.

The function f that appears in both boundary conditions is given by the

equation

f (x ) =



1, 0 < x < a,

0, a < x .

27. (Flow past a plate) A ﬂuid occupies the half-plane y > 0 and ﬂows past

(left to right, approximately) a plate located near the x-axis. If the x and y

components of velocity are U

+u(x, y) and v(x, y),respectively(U

constant free-stream velocity), under certain assumptions, the equations

of motion, continuity, and state can be reduced to

∂u

∂y

∂v

∂x



1 −M



∂u

∂x

∂v

∂y

=0,

valid for all x and y > 0. M is the free-stream Mach number. Deﬁne the

velocity potential φ by the equations u = ∂φ/∂x and v = ∂φ/∂y.Show

that the ﬁrst equation is automatically satisﬁed and the second is a partial

differential equation that is elliptic if M < 1 or hyperbolic if M > 1.

28. If the plate is wavy — say, its equation is y =  cos(αx) — then the

boundary condition, that the vector velocity be parallel to the wall, is



x,cos(αx)



=−α sin(αx)



x,cos(αx)



This equation is impossible to use, so it is replaced by

v(x, 0) =−αU

sin(αx)

290 Chapter 4 The Potential Equation

on the assumption that  is small and u is much smaller than U

. Using

this boundary condition and the condition that u(x, y) → 0asy →∞,

set up and solve a complete boundary value problem for φ,assuming

M < 1.

29. By superposition of solutions (α ranging from 0 to ∞) ﬁnd the ﬂow past

awallwhoseequationisy = f (x). Hint: Use the boundary condition

v(x, 0) = U



(x) =



∞



A(α) cos(αx) + B(α) sin(αx)



dα.

30. In hydrodynamics, the velocity vector in a ﬂuid is V =−grad(u),where

u is a solution of the potential equation. The normal component of ve-

locity, ∂u/∂n, is 0 at a wall. Thus the problem

∇

u =0, 0 < x < 1, 0 < y < 1,

∂u

∂x

(0, y) = 0,

∂u

∂x

(1, y) =−1, 0 < y < 1,

∂u

∂y

(x, 0) = 0,

∂u

∂y

(x, 1) = 1, 0 < x < 1,

represents a ﬂow around a corner: ﬂow inward at the top, outward at the

right, with walls at left and bottom. Explain why, in a ﬂuid ﬂow problem,

it must be true that



∂u

∂n

ds =0(∗)

if u is a solution of the potential equation in a region

R, ∂u/∂n is the

outward normal derivative,

C is the boundary of the region, and s is arc

length.

31. Under the conditions stated in Exercise 30, prove the validity of (∗).

Hint: Use Green’s theorem.

32. The Neumann problem consists of the potential equation in a region

and conditions on ∂u/∂n along C, the boundary of R . Show (a) that



∂u

∂n

ds =0

is a necessary condition for a solution to exist, and (b) if u is a solution

of the Neumann problem, so is u +c (c is constant).

33. Show that u(x, y) =

−x

) is a solution of the problem in Exercise 30.

34. a. Show that the given function is a solution of the potential equation.

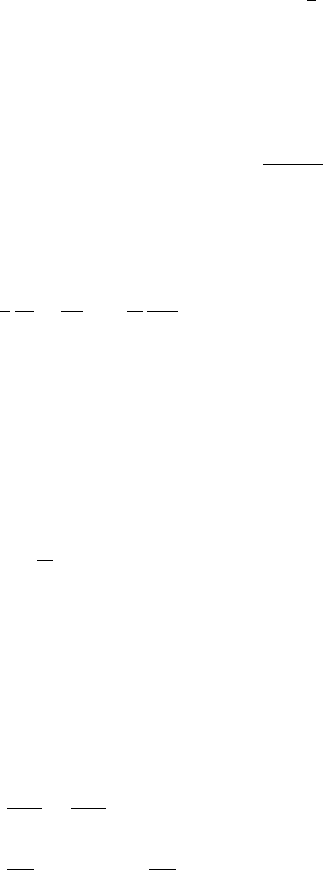
Miscellaneous Exercises 291

b. Find the gradient of u and plot some vectors V =−grad(u) near the

origin.

u(x, y) =−tan

−1





Theﬂowﬁeld(seeExercise30)givenbythisfunctioniscalledan

irrotational vortex.

35. SametasksasinExercise34.Theﬂowﬁeldgivenbythisfunctioniscalled

a source at the origin.

u(x, y) =−ln







36. Solve this potential problem in a half-annulus (sketch the region). At

some point, it may be useful to make the substitution s = ln(r).

∂

∂r



∂u

∂r



∂

∂θ

=0, 1 < r < e, 0 <θ<π,

u(1,θ)=0, u(e,θ)= 0, 0 <θ<π,

u(r, 0) = 0, u(r,π)=1, 1 < r < e.

37. Solve the Poisson equation, ∇

u =−f , in polar coordinates by ﬁnding a

function that depends only on r for:

a. f (r,θ)= 1;

b. f (r,θ)=

38. In “An improved transmission line structure for contact resistivity mea-

surements” [L.P. Floyd et al., Solid-State Electronics, 37 (1994): 1579–

1584], a strip of conducting material is carrying a current in the direc-

tion of its length. A second, long conducting strip of width L is placed at

right angles to the ﬁrst, forming a cross. A voltage is to be measured by

a probe on the second strip some distance from the ﬁrst. In the second

strip, the voltage V(x, y) satisﬁes the boundary value problem

∂

∂x

∂

∂y

=0, 0 < x < L, 0 < y,

∂V

∂x

(0, y) = 0,

∂V

∂x

(L, y) = 0, 0 < y,

V(x, 0) = f (x), 0 < x < L.

In this problem, x is in the direction of current ﬂow in the lower strip;

y is in the direction of the length of the second strip; y = 0attheedge

292 Chapter 4 The Potential Equation

Figure 4 Exercise 38.

of the lower strip (see Fig. 4). Of course, V is bounded as y →∞.Solve

this boundary value problem for V in terms of f (x).

39. The authors of the article cited in Exercise 38 say that any measurement

of V(x, y) made at a distance y greater than 5L is independent of x.Ex-

plain this statement, and determine what value (in terms of f ) would be

measured.

40. In the article “A production-planning and design model for assessing the

thermal behavior of thick steel strip during continuous heat treatment”

[W.D. Morris, Journal of Process Engineering (2001): 53–63] the author

models the temperature T(x, y) of a long steel strip that comes out of

an oven at x = 0, moving to the right, where it is exposed to coolant air.

These equations enter into the modeling (see Table 1 and Fig. 5):

a. Conservation of energy/steady-state heat equation, derived by con-

sidering conservation of energy for a rectangle of dimensions x by

y that is ﬁxed in space (see Sections 5.1 and 5.2):

∂T

∂x

∂

∂x

∂

∂y

, 0 < x, −b < y < b;

b. Symmetry condition:

∂T

∂y

(x, 0) = 0, 0 < x;

c. Cooling by convection at the surface (see Section 2.1, Eq. (10)):

−κ

∂T

∂y

(x, b) = h



T(x, b) −T



, 0 < x;

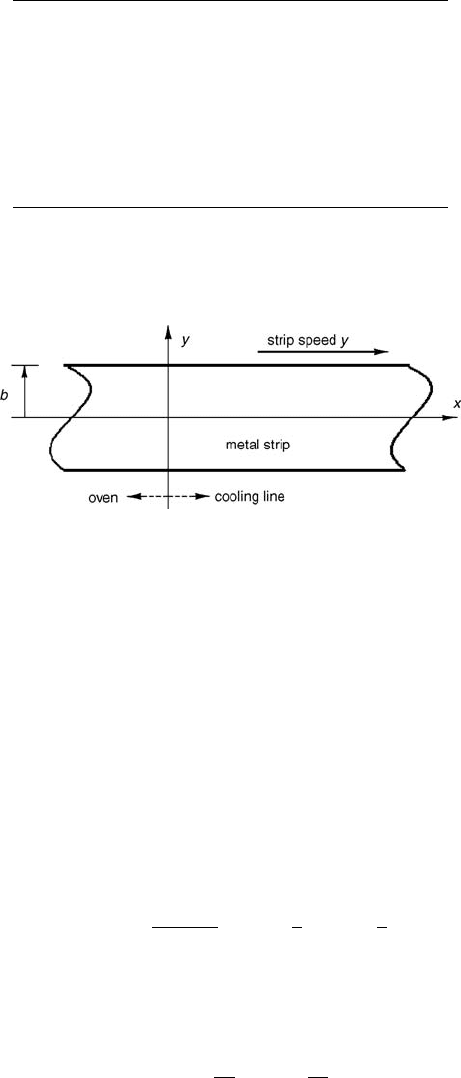
Miscellaneous Exercises 293

h convection coefﬁcient (W/m

κ thermal conductivity of steel (W/mK)

L length of cooling line

T(x, y) temperature in the strip

temperature of coolant

temperature of the strip at entry to cooling line

v strip speed (m/s)

k thermal diffusivity of steel (m

/s)

B Biot number (dimensionless)

Tab le 1 Table of Notation.

Figure 5 Exercise 40.

d. Condition at entry to cooling line (at x =0):

T(0, y) = T

, −b < y < b.

The author treats the strip as inﬁnite. In fact, typical dimensions are

100 m in the x-direction and 2 cm in the y-direction,sotheratioof

x to y lengths is on the order of 10

Next, these dimensionless variables are introduced:

θ =

T −T

−T

, Y =

, X =

and these dimensionless parameter combinations appear in the equa-

tions:

γ =

, B =

294 Chapter 4 The Potential Equation

The problem in terms of dimensionless variables and parameters is:

∂θ

∂X

∂

∂X

∂

∂Y

, 0 < X, 0 < Y < 1,

∂θ

∂Y

(X, 0) = 0, 0 < X,

∂θ

∂Y

(X, 1) =−Bθ(X, 1), 0 < X,

θ(0, Y) = 1, 0 < Y < 1.

SolvetheproblemforthecaseofahighBiotnumber,B →∞,which

means that θ(X, 1) = 0, 0 < X.

41. (Continuation) Solve the problem in Exercise 40 for the case of a low

Biot number, B ≈ 0, which means that

∂θ

∂Y

(X, 1) = 0, 0 < X.

Higher Dimensions

and Other

Coordinates

CHAPTER

5.1 Two-Dimensional Wave Equation: Derivation

For an example of a two-dimensional wave equation, we consider a membrane

that is stretched taut over a ﬂat frame in the xy-plane (Fig. 1). The displace-

ment of the membrane above the point (x, y) at time t is u(x, y, t).Weassume

that the surface tension σ (dimensions F/L) is constant and independent of

position. We also suppose that the membrane is perfectly ﬂexible; that is, it

does not resist bending. (A soap ﬁlm satisﬁes these assumptions quite accu-

rately.) Let us imagine that a small rectangle (of dimensions x by y aligned

with the coordinate axes) is cut out of the membrane, and then apply Newton’s

law of motion to it. On each edge of the rectangle, the rest of the membrane ex-

erts a distributed force of magnitude σ (symbolized by the arrows in Fig. 2a);

these distributed forces can be resolved into concentrated forces of magnitude

σx or σy, according to the length of the segment involved (see Fig. 2b and

Fig. 3).

Figure 1 Frame in the xy-plane.

295

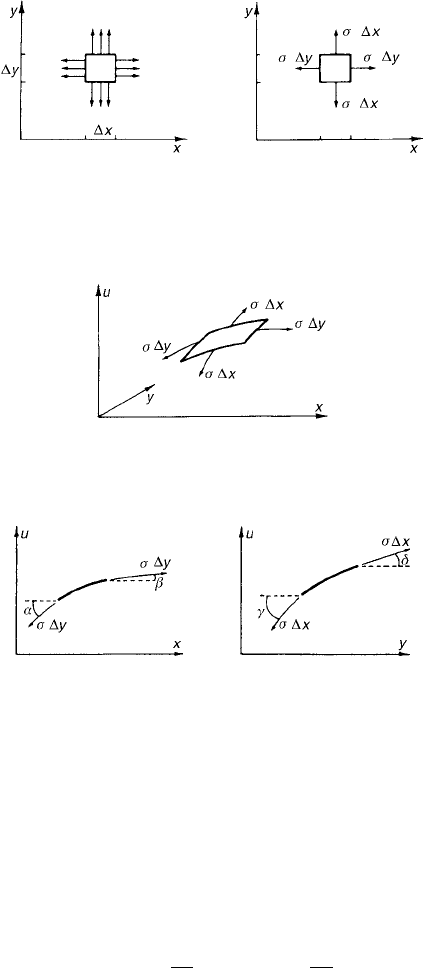
296 Chapter 5 Higher Dimensions and Other Coordinates

(a) (b)

Figure 2 (a) Distributed forces. (b) Concentrated forces.

Figure 3 Forces on a piece of membrane.

(a) (b)

Figure 4 Forces (a) in the xu-plane; (b) in the yu-plane.

Looking at projection on the xu-andyu-planes (Figs. 4a, 4b), we see that

the sum of forces in the x-direction is σy(cos(β) −cos(α)),andthesumof

forces in the y-direction is x(cos(δ) −cos(γ )). It is desirable that both these

sums be zero or at least negligible. Therefore we shall assume that α, β, γ ,and

δ are all small angles. Because we know that

tan(α) =

∂u

∂x

, tan(γ ) =

∂u

∂y

and so forth, when the derivatives are evaluated at some appropriate point near

(x, y), we are assuming that the slopes ∂u/∂x and ∂u/∂y of the membrane are

very small.

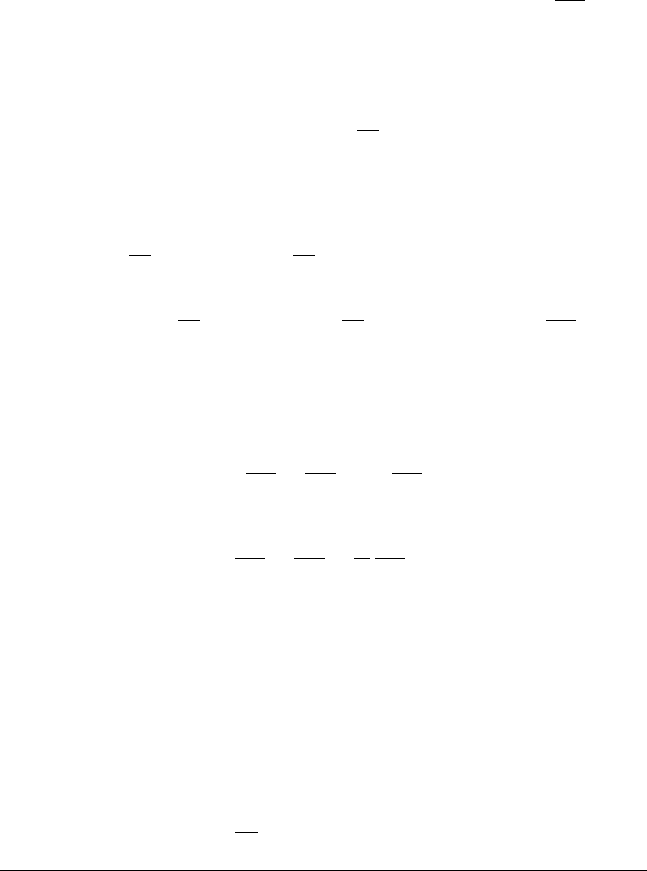
Chapter 5 Higher Dimensions and Other Coordinates 297

Adding up forces in the vertical direction and equating the sum to the mass

times acceleration (in the vertical direction) we obtain

σy



sin(β) − sin(α)



+σx



sin(δ) −sin(γ )



=ρx y

∂

∂t

where ρ is the surface density [m/L

]. Because the angles α, β, γ ,andδ are

small, the sine of each is approximately equal to its tangent:

sin(α)

∼

tan(α) =

∂u

∂x

(x, y, t),

and so forth. With these approximations used throughout, the preceding equa-

tion becomes

σy



∂y

∂x

(x +x, y, t) −

∂u

∂x

(x, y, t)



+σx



∂u

∂y

(x, y + y, t) −

∂u

∂y

(x, y, t)



=ρx y

∂

∂t

On dividing through by x y, we recognize two difference quotients in

the left-hand member. In the limit they become partial derivatives, yielding

the equation



∂

∂x

∂

∂y



=ρ

∂

∂t

∂

∂x

∂

∂y

∂

∂t

if c

=σ/ρ. This is the two-dimensional wave equation.

If the membrane is ﬁxed to the ﬂat frame, the boundary condition would be

u(x, y, t) = 0 for (x, y) on the boundary.

Naturally, it is necessary to give initial conditions describing the displacement

and velocity of each point on the membrane at t =0:

u(x, y, 0) = f (x, y),

∂u

∂t

(x, y, 0) = g(x, y).

EXERCISES

1. Suppose that the frame is rectangular, bounded by segments of the lines

x = 0, x = a, y = 0, y = b. Write an initial value–boundary value problem,

complete with inequalities, for a membrane stretched over this frame.