Powers D.L. Boundary Value Problems and Partial Differential Equations

Подождите немного. Документ загружается.

278 Chapter 4 The Potential Equation

ThesolutionisgivenbyEq.(10),providedthatthecoefﬁcientsarechosen

accordingtoEq.(11).Sincef (θ ) is an even function, b

=0, and



f (θ) dθ =

πc



f (θ) cos(nθ)dθ =

2sin(nπ/2)

nπc

Therefore, the solution of the problem is

v(r,θ)=

∞



n=1

2sin(nπ/2)

nπ

cos(nθ). (12)

The level curves of this function are all arcs of circles that pass through the

boundary points r = c, θ =±π/2, where f (θ) jumps between 0 and 1. Along

the x-axis, the function has the simple closed form 1/2 +(2/π ) tan

−1

(x/c).

The CD has a color graphic of the solution.



Properties of the Solution

Now that we have the form Eq. (10) of the solution of the potential equation,

we can see some important properties of the function v(r,θ).Inparticular,by

setting r =0weobtain

v(0,θ)=a

2π



−π

f (θ) dθ =

2π



−π

v(c,θ)dθ.

This says that the solution of the potential equation at the center of a disk is

equal to the average of its values around the edge of the disk. It is easy to show

also that

v(0,θ)=

2π



−π

v(r,θ)dθ (13)

for any r between 0 and c! This characteristic of solutions of the potential equa-

tion is called the mean value property. From the mean value property, it is just

a step to prove the maximum principle mentioned in Section 4.1, for the mean

value of a function lies between the minimum and the maximum and cannot

equal either unless the function is constant.

An important consequence of the maximum principle — and thus of the

mean value property — is a proof of the uniqueness of the solution of the

Dirichlet problem. Suppose that u and v are two solutions of the potential

equation in some region R and that they have the same values on the bound-

ary of R. Then their difference, w = u − v, is also a solution of the potential

equation in R and has value 0 all along the boundary of R.Bythemaximum

4.5 Potential in a Disk 279

principle, w has maximum and minimum values 0, and therefore w is identi-

cally 0 throughout R .Inotherwords,u and v are identical.

EXERCISES

1. Solve the potential equation in the disk 0 < r < c if the boundary condi-

tion is v(c,θ)=|θ |, −π<θ≤ π .

2. Same as Exercise 1 if v(c,θ)=θ , −π<θ<π. Is the boundary condition

satisﬁed at θ =±π?

3. Same as Exercise 1, with boundary condition

v(c,θ)= f (θ ) =



cos(θ), −π/2 <θ<π/2,

0, otherwise.

4. Find the value of the solution at r = 0 for the problems of Exercises 1, 2,

and 3.

5. If the function f (θ) in Eq. (2) is continuous and sectionally smooth and

satisﬁes f (−π+) = f (π−), what can be said about convergence of the

series for v(c,θ)?

6. Show that

v(r,θ)= a

∞



n=1

−n



cos(nθ)+b

sin(nθ)



is a solution of Laplace’s equation in the region r > c (exterior of a disk)

and has the property that |v(r,θ)| is bounded as r →∞.

7. If the condition v(c,θ)= f (θ) is given, what are the formulas for the a’s

and b’s in Exercise 6?

8. The solution of Eqs. (1)–(4) can be written in a single formula by the

following sequence of operations:

a. Replace θ by φ in Eq. (11) for the a’s and b’s;

b. replace the a ’s and b’s in Eq. (10) by the integrals in part a;

c. use the trigonometric identity

cos(nθ)cos(nφ) +sin(nθ)sin(nφ) = cos



n(θ −φ)



;

d. take the integral outside the series;

280 Chapter 4 The Potential Equation

add up the series (see Section 1.10, Exercise 5a). Then v(r,θ) is given

by the single integral (Poisson integral formula)

v(r,θ)=

2π



−π

f (φ)

−r

−2rc cos(θ −φ)

dφ.

9. Solve Laplace’s equation in the quarter-disk 0 <θ<π/2, 0 < r < c,sub-

ject to the boundary conditions v(r, 0) = 0, v(r,π/2) = 0, v(c ,θ)= 1.

10. Generalize the results of Exercise 9 by solving this problem:

∂

∂r



∂v

∂r



∂

∂θ

=0, 0 <θ<απ, 0 < r < c,

v(r, 0) = 0,v(r,απ)= 0, 0 < r < c,

v(c,θ)= f (θ ), 0 <θ<απ.

Here, α is a parameter between 0 and 2.

11. Suppose that α>1 in Exercise 10. Show that there is a product solution

with the property that

∂v

∂r

(r,θ) is not bounded as r → 0+.

4.6 Classiﬁcation of Partial Differential Equations

and Limitations of the Product Method

By this time, we have seen a variety of equations and solutions. We have con-

centrated on three different, homogeneous equations (heat, wave, and poten-

tial) and have found the qualitative features summarized in the following table:

Equation Features

Heat Exponential behavior in time. Existence of a limiting (steady-state) solution.

Smooth graph for t > 0.

Wave Oscillatory (not always periodic) behavior in time. Retention of discontinuities

for t > 0.

Potential Smooth surface. Maximum principle. Mean value property.

These three two-variable equations are the most important representatives

of the three classes of second-order linear partial differential equations in two

variables. The most general equation that ﬁts this description is

∂

∂ξ

∂

∂ξ∂η

∂

∂η

∂u

∂ξ

∂u

∂η

+Fu +G =0,

4.6 Classiﬁcation and Limitations 281

where A, B, C, and so forth are, in general, functions of ξ and η.(WeuseGreek

letters for the independent variables to avoid implying any relations to space

or time.) Such an equation can be classiﬁed according to the sign of B

−4AC:

−4AC < 0: elliptic,

−4AC = 0: parabolic,

−4AC > 0: hyperbolic.

Because A, B, and C are functions of ξ and η (not of u), the classiﬁcation of an

equation may vary from point to point. It is easy to see that the heat equation

is parabolic, the wave equation is hyperbolic, and the potential equation is

elliptic. The classiﬁcation of an equation determines important features of the

solution and also dictates the method of attack when numerical techniques are

used for solution.

The question naturally arises whether separation of variables works on all

equations. The answer is no. For instance, the equation



ξ +η



∂

∂ξ

∂

∂η

does not admit separation of variables. In general, it is difﬁcult to say just

which equations can be solved by this method. However, it is necessary to have

B ≡0.

The region in which the solution is to be found also limits the applicability

ofthemethodwehaveused.Theregionmustbeageneralized rectangle.By

this we mean a region bounded by coordinate curves of the coordinate system

of the partial differential equation. Put another way, the region is described

by inequalities on the coordinates, whose endpoints are ﬁxed quantities. For

instance, we have worked in regions described by the following sets of inequal-

ities:

0 < x < a, 0 < t,

0 < x, 0 < t,

−∞< x < ∞, 0 < t,

0 < x < a, 0 < y < b,

0 < r < c, −π<θ≤ π.

All of these are generalized rectangles, but only one is an ordinary rectangle.

An L-shaped region is not a generalized rectangle, and our methods would

break down if applied to, for instance, the potential equation there.

There are, as we know, restrictions on the kinds of boundary conditions

that can be handled. From the examples in this chapter it is clear that we need

282 Chapter 4 The Potential Equation

homogeneous or “homogeneous-like” conditionsonoppositesidesofagener-

alized rectangle. Examples of “homogeneous-like” conditions are the require-

ment that a function remain bounded as some variable tends to inﬁnity, or the

periodic conditions at θ =±π (see Section 4.5). The point is that if two or

more functions satisfy the conditions, so does a sum of those functions.

In spite of the limitations of the method of separation of variables, it works

well on many important problems in two or more variables and provides in-

sight into the nature of their solutions. Moreover, it is known that in those

cases where separation of variables can be carried out, it will ﬁnd a solution if

one exists.

EXERCISES

1. Classify the following equations.

∂

∂x∂y

=0;

∂

∂x

∂

∂x∂y

∂

∂y

=2x;

∂

∂x

−

∂

∂x∂y

∂

∂y

=2u;

∂

∂x

−2

∂

∂x∂y

∂

∂y

∂u

∂y

;

∂

∂x

−

∂

∂y

−

∂u

∂y

=0.

2. Showthat,inpolarcoordinates,anannulus,asector,andasectorofan

annulus are all generalized rectangles.

3. InwhichoftheequationsinExercise1canthevariablesbeseparated?

4. Sketch the regions listed in the text as generalized rectangles.

5. Solve these three problems and compare the solutions.

∂

∂x

∂

∂y

=0, 0 < x < 1, 0 < y,

u(x, 0) = f (x),0< x < 1,

u(0, y) = 0, u(1, y) = 0, 0 < y;

∂

∂x

∂

∂y

,0< x < 1, 0 < y,

4.7 Comments and References 283

u(x, 0) = f (x),

∂u

∂y

(x, 0) = 0, 0 < x < 1,

u(0, y) = 0, u(1, y) = 0, 0 < y;

∂

∂x

∂u

∂y

,0< x < 1, 0 < y,

u(x, 0) = f (x),0< x < 1,

u(0, y) = 0, u(1, y) = 0, 0 < y.

6. Show that if f

, f

,...all satisfy the periodic boundary conditions

f (−π) = f (π ), f



(−π)= f



(π),

then so does the function c

+···,wherethec’s are constants.

7. Longitudinal waves in a slender rod may be described by this partial differ-

ential equation:

∂

∂x

∂

∂t

−

∂

∂x

∂t

Show how to separate the variables.

8. Deﬂections of a thin plate and slow ﬂow of a viscous ﬂuid may both be

described by the biharmonic equation

∂

∂x

∂

∂x

∂y

∂

∂y

=0.

Assume that u(x, y) = X(x)Y(y) and show that the variables don’t separate.

Show that, under the additional assumption X



/X =−λ

, a differential

equation for Y results.

4.7 Comments and References

While the potential equation describes many physical phenomena, there is one

that makes the solution of the Dirichlet problem very easy to visualize. Sup-

pose a piece of wire is bent into a closed curve or frame. When the frame is

held over a level surface, its projection onto the surface is a plane curve

C en-

closing a region

R. If one forms a soap ﬁlm on the frame, the height u(x, y) of

the ﬁlm above the level surface is a function that satisﬁes the potential equa-

tion approximately, if the effects of gravity are negligible (see Chapter 5). The

height of the frame above the curve

C gives the boundary condition on u.For

example, Fig. 2(b) shows the surface corresponding to the problem solved in

Section4.2.AgreatdealofinformationaboutsoapﬁlmsisinthebookThe

ScienceofSoapFilmsandSoapBubblesby C. Isenberg (see the Bibliography).

284 Chapter 4 The Potential Equation

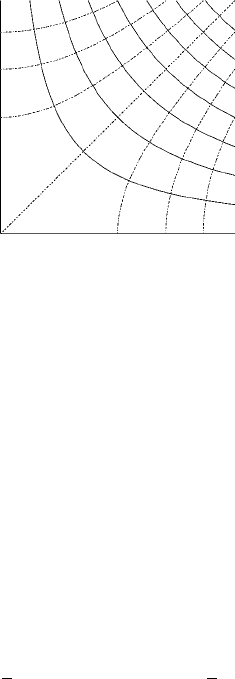
Figure 3 Streamlines (solid) and equipotential curves (dashed) for ﬂow in a cor-

ner. The streamlines are described by the equation 2xy = constant, with a differ-

ent constant for each one. Similarly, the equipotential curves are described by the

equation x

−y

=constant.

It turns out that the potential equation (but not all elliptic equations) is

best studied through the use of complex variables. A complex variable may be

written z = x +iy,wherex and y are real and i

=−1; similarly a function of

z is denoted by f (z) = u(x, y) + iv(x, y), u and v being real functions of real

variables. If f has a derivative with respect to z,thenbothu and v satisfy the

potential equation. Easy examples, such as polynomials and exponentials, lead

to familiar solutions:

= (x + iy)

−y

+i2xy,

= e

x+iy

cos(y) + ie

sin(y),

ln(z) =





+i tan

−1





(See Section 4.1, Exercises 1, 2; Section 4.4, Exercises 13, 14; Miscellaneous

Exercise 18 in this chapter.) Knowing these elementary solutions often helps

in simplifying a problem.

In certain idealized ﬂuid ﬂows (steady, irrotational, two-dimensional ﬂow of

an inviscid, incompressible ﬂuid) the velocity vector is given by V =−grad φ,

where the velocity potential φ is a solution of the potential equation. The

streamlines along which the ﬂuid ﬂows are level curves of a related function ψ,

called the stream function, which also is a solution of the potential equation.

The two functions φ and ψ are, respectively, the real and imaginary parts

of a function of the complex variable z. The level curves φ = constant and

ψ = constant form two families of orthogonal curves called a ﬂow net.The

ﬂow net in Fig. 3, for φ =x

−y

and ψ = 2xy (the real and imaginary parts

of the function f (z) = z

), illustrates ﬂow near a corner formed by two walls.

Many other ﬂow nets are shown in the book Potential Flows: Computer Graphic

Solutions by R.H. Kirchhoff. Civil engineers sometimes sketch a ﬂow net by eye

Miscellaneous Exercises 285

to get a rough graphical solution of the potential equation for hydrodynamics

problems.

Where a physical boundary is formed by an impervious wall, the velocity

vector V must be parallel to the boundary. This fact leads to two boundary

conditions. First, the wall must coincide with a streamline; thus ψ = constant

along a boundary. Second, the component of V that is normal to the wall must

be zero there, because no ﬂuid passes through it; thus the normal derivative of

φ is zero, ∂φ/∂n = 0, at a boundary. See Miscellaneous Exercises 30–32.

Chapter Review

See the CD for Review Questions.

Miscellaneous Exercises

1. Solve the potential equation in the rectangle 0 < x < a,0< y < b with

the boundary conditions

u(0, y) = 1, u(a, y) = 0, 0 < y < b,

u(x, 0) = 0, u(x, b ) = 0, 0 < x < a.

2. If a = b in Exercise 1, then u(a/2, a/2) = 1/4. Use symmetry to explain

this fact.

3. Solve the potential equation on the rectangle 0 < x < a,0< y < b with

the boundary conditions

u(0, y) = 1, u(a, y) =1, 0 < y < b,

∂u

∂y

(x, 0) = 0,

∂u

∂y

(x, b) = 0, 0 < x < a.

4. Same as Exercise 3, but the boundary conditions are

u(0, y) = 1,

∂u

∂x

(a, y) = 0, 0 < y < b,

u(x, 0) = 1,

∂u

∂y

(x, b) = 0, 0 < x < a.

286 Chapter 4 The Potential Equation

5. Same as Exercise 3, but the boundary conditions are

u(0, y) = 1, u(a, y) = 1, 0 < y < b,

∂u

∂y

(x, 0) = 0, u(x, b) = 0, 0 < x < a.

6. Same as Exercise 3, but the boundary conditions are

u(0, y) = 1, u(a, y) =0, 0 < y < b,

u(x, 0) = 1, u(x, b) =0, 0 < x < a.

7. Same as Exercise 3, but the region is a square (b = a) and the boundary

conditions are

u(0, y) = f (y), u(a, y) = 0, 0 < y < a,

u(x, 0) = f (x), u(x, a) = 0, 0 < x < a,

where f is a function whose graph is an isosceles triangle of height h and

width a.

8. Solve the potential equation in the region 0 < x < a,0< y with the

boundary conditions

u(x, 0) = 1, 0 < x < a,

u(0, y) = 0, u(a, y) =0, 0 < y.

9. Find the solution of the potential equation on the strip 0 < y < b,

−∞ < x < ∞, subject to the conditions that follow. Supply bounded-

ness conditions as necessary.

u(x, 0) =



1, −a < x < a,

0, |x| > a,

u(x, b) = 0, −∞ < x < ∞.

10. Show that the function u(x, y) = tan

−1

(y/x) is a solution of the potential

equation in the ﬁrst quadrant. What conditions does u satisfy along the

positive x-andy-axes?

11. Solve the potential problem in the upper half-plane,

∂

∂x

∂

∂y

=0, −∞ < x < ∞, 0 < y,

u(x, 0) = f (x), −∞ < x < ∞,

taking f (x) = exp(−α|x|).

Miscellaneous Exercises 287

12. Apply the following formula (see Section 4.4, Exercise 16) for the solu-

tion of the potential problem in the upper half-plane if the boundary

condition is u(x, 0) = f (x),where

f (x ) =



0, x < 0,

1, x > 0,

u(x, y) =



∞

−∞

f (x



)

+(x −x



)



13. Apply the formula in Exercise 12 to the case where f (x) = 1, −∞ < x

< ∞. The solution of the problem should be u(x, y) ≡ 1.

14. a. Find the separation-of-variables solution of the potential problem in

a disk of radius 1 if the boundary condition is u(1,θ)=f (θ ),where

f (θ) =



−π −θ, −π<θ<0,

π −θ, 0 <θ<π.

b. Show that the function given in polar and Cartesian coordinates by

u(r,θ)= 2tan

−1



r sin(θ)

1 −r cos(θ)



= 2tan

−1



1 −x



satisﬁes the potential equation (use the Cartesian coordinates) and

the boundary condition. The following identity is useful:

sin(θ)

1 −cos(θ )

=tan



π −θ



c. Sketch some level curves of the solution inside the circle of radius 1.

15. Solve the potential equation in a disk of radius c with boundary condi-

tions

u(c,θ)=



1, 0 <θ<π,

0, −π<θ<0.

16. What is the value of u at the center of the disk in Exercise 15?

17. Same as Exercise 15, but the boundary condition is

u(c,θ)=



sin(θ)

