Powers D.L. Boundary Value Problems and Partial Differential Equations

Подождите немного. Документ загружается.

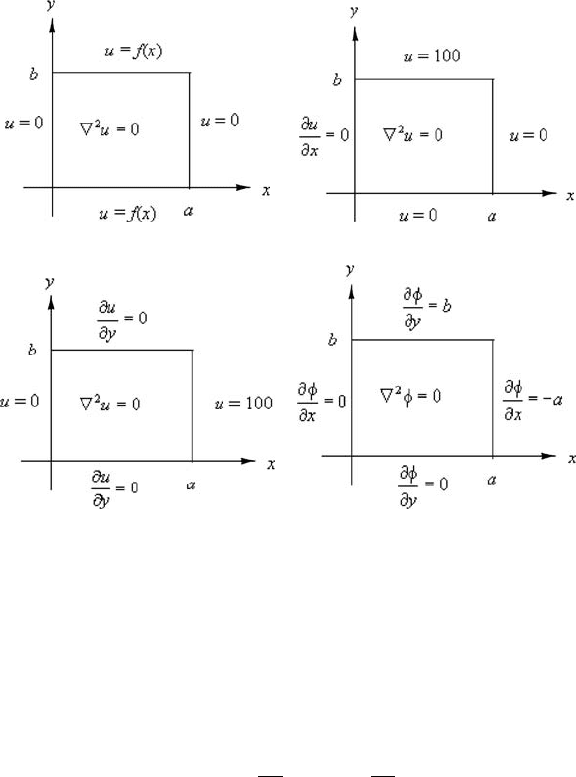
258 Chapter 4 The Potential Equation

(a) (b)

Figure 1 (a) u is displacement of a membrane; the graph of f (x) is an isosceles

triangle. (b) u is the temperature on a cross section of a long bar. (c) u is voltage

in a rectangular sheet of conducting material. (d) φ is a velocity potential (see

Exercise 8). What are x-andy-velocities on the boundaries?

Show that the deﬁnition of a velocity potential function φ by the equations

u =−

∂φ

∂x

,v=−

∂φ

∂y

causes (B) to be identically satisﬁed and turns (A) into the potential equa-

tion. (See Section 4.7, Comments and References, at the end of this chap-

ter.)

9. For each of the diagrams in Fig. 1, (a) write out the problem in mathemat-

ical form (partial differential equation and boundary conditions); (b) pro-

vide an interpretation in words of the boundary conditions for the given

interpretation of the unknown function.

4.2 Potential in a Rectangle 259

4.2 Potential in a Rectangle

One of the simplest and most important problems in mathematical physics is

Dirichlet’s problem in a rectangle. To take an easy case, we consider a problem

with just two nonzero boundary conditions:

∂

∂x

∂

∂y

=0, 0 < x < a, 0 < y < b, (1)

u(x, 0) = f

(x), 0 < x < a, (2)

u(x, b) = f

(x), 0 < x < a, (3)

u(0, y) = 0, 0 < y < b, (4)

u(a, y) = 0, 0 < y < b. (5)

It is not immediately clear that separation of variables will work. However,

we have a homogeneous partial differential equation and some homogeneous

boundary conditions, so we can try the method. If we assume that u(x, y) has

a product form u = X(x)Y(y),thenEq.(1)becomes



(x)Y(y) +X(x)Y



(y) = 0.

This equation can be separated by dividing through by XY to yield



(x)

X(x)

=−



(y)

Y(y )

. (6)

The nonhomogeneous conditions Eqs. (2) and (3) will not, in general, become

conditions on X or Y, but the homogeneous conditions Eqs. (4) and (5), as

usual, require that

X(0) = 0, X(a) = 0. (7)

Now, both sides of Eq. (6) must be constant, but the sign of the constant

is not obvious. If we try a positive constant (say, µ

), Eq. (6) represents two

ordinary equations:



−µ

X = 0, Y



+µ

Y = 0.

The solutions of these equations are

X(x) = A cosh(µx) +B sinh(µx), Y(y) =C cos(µy) +D sin(µy).

In order to make X satisfy the boundary conditions Eq. (7), both A and B must

be zero, leading to a solution u(x, y) ≡ 0. Thus we try the other possibility for

sign, taking both members in Eq. (6) to equal −λ

260 Chapter 4 The Potential Equation

Under the new assumption, Eq. (6) separates into



+λ

X = 0, Y



−λ

Y = 0. (8)

The ﬁrst of these equations, along with the boundary conditions, is recogniz-

able as an eigenvalue problem, whose solutions are

(x) = sin(λ

x), λ



nπ



The functions Y that accompany the X’s are

(y) = a

cosh(λ

y) +b

sinh(λ

y).

The a’s and b’s are for the moment unknown.

We s ee t hat X

(x)Y

(y) is a solution of the (homogeneous) potential Eq. (1),

which satisﬁes the homogeneous conditions Eqs. (4) and (5). A sum of these

functions should satisfy the same conditions and equation, so u may have the

form

u(x, y) =

∞



n=1



cosh(λ

y) +b

sinh(λ



sin(λ

x). (9)

The nonhomogeneous boundary conditions Eqs. (2) and (3) are yet to be

satisﬁed. If u is to be of the form of Eq. (9), the boundary condition Eq. (2)

becomes

u(x, 0) =

∞



n=1

sin



nπx



(x), 0 < x < a. (10)

We recognize a problem in Fourier series immediately. The a

must be the

Fourier sine coefﬁcients of f

(x),



(x) sin



nπx



dx.

The second boundary condition reads

u(x, b) =

∞



n=1



cosh(λ

b) +b

sinh(λ



sin



nπx



= f

(x), 0 < x < a.

This also is a problem in Fourier series, but it is not as neat. The constant

cosh(λ

b) +b

sinh(λ

4.2 Potential in a Rectangle 261

must be the nth Fourier sine coefﬁcient of f

.Sincea

is known, b

can be

determined from the following computations:

cosh(λ

b) +b

sinh(λ

b) =



(x) sin(λ

x) dx = c

−a

cosh(λ

sinh(λ

If we use this last expression for b

and substitute into Eq. (9), we ﬁnd the

solution

u(x, y) =

∞



n=1



sinh(λ



cosh(λ

y) −

cosh(λ

sinh(λ



sin(λ

x). (11)

Notice that the function multiplying c

is 0 at y = 0andis1aty = b. Similarly,

the function multiplying a

is 1 at y =0and0aty = b. An easier way to write

this latter function is

sinh(λ

(b −y))

sinh(λ

as can readily be found from hyperbolic identities.

Example.

Suppose f

and f

are both given by

(x) = f

(x) =











, 0 < x <



a −x



< x < a.

Then

sin(nπ/2)

The solution of the potential equation for these boundary conditions is

u(x, y) =

∞



n=1

sin



nπ



sinh



nπ



+sinh



nπ

(b −y)



sinh



nπb



sin



nπx



. (12)

In Fig. 2 is a graph of some level curves, u(x, y) =constant, for the case where

a = b, and also a view of the surface z = u(x, y). Also see color ﬁgures on the

CD.



262 Chapter 4 The Potential Equation

(a) (b)

Figure 2 (a) Level curves of the solution u(x, y) of the example problem (see

Eq. (12)) for the case b = a = 1. Each curve is part of the locus of points that

satisfy u(x, y) = constant for constants 0 to 0.9 in steps of 0.1. For some constants,

the locus consists of more than one connected curve. (b) Perspective view of the

surface z =u(x, y).

Now we have seen a solution of Dirichlet’s problem in a rectangle with ho-

mogeneous conditions on two parallel sides. In general, of course, the bound-

ary conditions will be nonhomogeneous on all four sides of the rectangle. But

this more general problem can be broken down into two problems like the one

we have solved.

Consider the problem

∇

u =0, 0 < x < a, 0 < y < b , (13)

u(x, 0) = f

(x), 0 < x < a, (14)

u(x, b) = f

(x), 0 < x < a, (15)

u(0, y) = g

(y), 0 < y < b, (16)

u(a, y) = g

(y), 0 < y < b. (17)

Let u(x, y) = u

(x, y) + u

(x, y). We will put conditions on u

and u

so that

they can readily be found, and from them u can be put together. The most

obvious conditions are the following:

∇

=0, ∇

=0,

(x, 0) = f

(x), u

(x, 0) = 0,

(x, b) = f

(x), u

(x, b) = 0,

(0, y) = 0, u

(0, y) = g

(y),

(a, y) = 0, u

(a, y) = g

(y).

4.2 Potential in a Rectangle 263

It is evident that u

+ u

is the solution of the original problem Eqs. (13)–

(17). Also, each of the functions u

and u

has homogeneous conditions on

parallel boundaries. We already have determined the form of u

. The other

function would be of the form

(x, y) =

∞



n=1

sin(µ

sinh(µ

x) +B

sinh(µ

(a −x))

sinh(µ

, (18)

where µ

=nπ/b and



(y) sin(µ

y) dy,



(y) sin(µ

y) dy.

In the individual problems for u

and u

, the technique of separation of

variable works because the homogeneous conditions on parallel sides of the

rectangle can be translated into conditions on one of the factor functions.

When the boundary conditions are not complicated functions, it may be

possible to satisfy some of them with a polynomial function. (See Exercises 1

and 2 of Section 4.1.) Then the difference between u and the polynomial is a

solution of the potential equation that satisﬁes some homogeneous boundary

conditions.

EXERCISES

1. Show that sinh(λy) and sinh(λ(b − y)) are independent solutions of



−λ

Y = 0 with λ = 0. Thus a combination of these two functions may

replace a combination of sinh and cosh as the general solution of this dif-

ferential equation.

2. Show that the solution of the example problem may be written

u(x, y) =

∞



n=1

sin



nπ



cosh



nπ

(y −



cosh



nπb



sin



nπx



3. Use the form in Exercise 2 to compute u in the center of the rectangle in

the three cases b = a, b = 2a, b = a/2. (Hint: Check the magnitude of the

terms.)

4. Verify that each term of Eq. (9) satisﬁes Eqs. (1), (4), and (5).

264 Chapter 4 The Potential Equation

Solve the problem

∇

u =0, 0 < x < a, 0 < y < b,

u(0, y) = 0, u(a, y) =0, 0 < y < b,

u(x, 0) = 0, u(x, b ) =f (x), 0 < x < a,

where f is the same as in the example. Sketch some level curves of u(x, y).

6. Solve the potential problem on the rectangle 0 < x < a,0< y < b,subject

to the boundary conditions u(a, y) = 1, 0 < y < b,andu = 0ontherestof

the boundary.

7. Solve the problem of the potential equation in the rectangle 0 < x < a,0<

y < b, for each of the following sets of boundary conditions. Before solving,

make a pictorial version of the problem as in Exercise 9 of Section 4.1.

a. u(x, b) =100, 0 < x < a; u = 0 on the other three sides of the rectangle.

b. u(x, b) = 100, 0 < x < a; u(a, y) = 100, 0 < y < b; u = 0 on the other

two sides of the rectangle.

c. u(x, b) = bx,0< x < a; u(a, y) = ay,0< y < b; u = 0 on the other two

sides of the rectangle.

8. Solve the problem for u

.(Thatis,deriveEq.(18).)

4.3 Further Examples for a Rectangle

In Section 4.2, we solved Dirichlet problems with separation of variables. The

same method applies to problems with other types of boundary conditions, as

shown in the following.

Example 1.

In this problem, the unknown function might be a voltage in a conductor. The

left and right sides are electrically insulated.

∂

∂x

∂

∂y

=0, 0 < x < a, 0 < y < b,

∂u

∂x

(0, y) = 0,

∂u

∂x

(a, y) = 0, 0 < y < b,

u(x, 0) = 0, u(x, b) = V

x/a, 0 < x < a.

We have homogeneous conditions on the facing sides at x = 0andx = a.If

we look for solutions in the product form u(x, y) = X(x)Y(y),weﬁnd(asex-

4.3 Further Examples for a Rectangle 265

pected) that



(x)

X(x)

=−



(y)

Y(y )

=constant.

The conditions at x =0andx =a become



(0) = 0, X



(a) =0.

If we make the separation constant −λ

, we ﬁnd a familiar eigenvalue problem

for X whose solution is

(x) = 1,λ

=0,

(x) = cos(λ

x), λ

=nπ/a, n = 1, 2,....

For the factor Y(y), the differential equation is



=0, or Y



−λ

with solution

(y) = a

y or Y

(y) = a

cosh(λ

y) +b

sinh(λ

y).

Thus, the principle of superposition leads to the series solution

u(x, y) = a

y +

∞



n=1



cosh(λ

y) +b

sinh(λ



cos(λ

x).

The boundary condition at y =0becomes

∞



cos(λ

x) = 0, 0 < x < a,

from which we see that all the a’s are 0. Then at y = b we have

b +

∞



n=1



sinh(λ



cos(λ

x) =

, 0 < x < a.

This is a slightly disguised cosine series. The coefﬁcients are

b =







dx,

sinh(λ

b) =







cos(λ

x) dx.

See a color graphic of the solution on the CD.



266 Chapter 4 The Potential Equation

We have seen that the success of the separation of variables method depends

on having homogeneous boundary conditions at the ends of one of the inter-

vals involved. In Section 4.2 we mentioned splitting up a Dirichlet problem,

if necessary, to achieve this. The same splitting technique applies in problems

where boundary condition of other kinds are used. The principle is to zero

conditions on two facing sides of the region and to copy the rest.

Example 2.

This problem may describe the temperature u(x, y) in a thin plate between

insulating sheets.

∂

∂x

∂

∂y

=0, 0 < x < a, 0 < y < b,

∂u

∂x

(0, y) = 0, u(a, y) = Sy, 0 < y < b,

∂u

∂y

(x, 0) = S, u(x, b) =

Sbx

, 0 < x < a.

Since we have nonhomogeneous conditions on adjacent sides, we must split

the problem in order to solve by separation of variables. Here are the two prob-

lems:

∂

∂x

∂

∂y

=0,

∂

∂x

∂

∂y

=0,

∂u

∂x

(0, y) = 0, u

(a, y) = 0,

∂u

∂x

(0, y) = 0, u

(a, y) = Sy,

∂u

∂y

(x, 0) = S, u

(x, b) =

Sbx

∂u

∂y

(x, 0) = 0, u

(x, b) = 0.

The solution of the original problem is the sum u = u

+ u

.Hereisthe

reasoning in detail.

1. The potential equation is linear and homogeneous. By the Principle of

Superposition, the sum of solutions is a solution.

2. At x = a we have u(a, y) = 0 + Sy,andaty = b we have u(x, b) =

Sbx/a + 0. Both conditions are satisﬁed.

3. From elementary calculus, we know

∂u

∂x

∂u

∂x

∂u

∂x

∂u

∂y

∂u

∂y

∂u

∂y

4.3 Further Examples for a Rectangle 267

Then at the left and bottom boundaries, we have

∂u

∂x

(0, y) =0 +0,

∂u

∂y

(x, 0) = S +0.

These are satisﬁed as well.

Thus, it remains to solve the two problems for u

and u

. (See the Exercises.)

Here are product solutions. For u

cos(λ



cosh(λ

y) +b

sinh(λ



,λ



n −



, n =1, 2,....

For u

cos(µ



cosh(µ

x) +B

sinh(µ



,µ



n −



, n =1, 2,....



The simple polynomial solutions that we found in Section 4.1, Exercise 1,

can be very useful in reducing the number of series needed for a solution. If

nonhomogeneous conditions are given on adjacent sides and these are con-

stants or ﬁrst-degree polynomials in one variable, then a polynomial may be

able to satisfy enough of them to simplify the work.

Example 3.

Refer to the problem in Example 2. The polynomial v(y) = Sy satisﬁes the

potential equation and several of the boundary conditions:

∂v

∂x

(0, y) = 0,v(a, y) = Sy, 0 < y < b,

∂v

∂y

(x, 0) = S,v(x, b) = Sb, 0 < x < a.

Thus, we may set u(x, y) = v(y) + w(x, y) and determine that w must be the

solution of this problem, similar to the problem for u

in Example 2:

∂

∂x

∂

∂y

=0, 0 < x < a, 0 < y < b,

∂w

∂x

(0, y) = 0,w(a, y) = 0, 0 < y < b,

∂w

∂y

(x, 0) = 0,w(x, b) =

Sb(x − a)

, 0 < x < a.

Thesolutionisleftasanexercise.

