Powers D.L. Boundary Value Problems and Partial Differential Equations

Подождите немного. Документ загружается.

218 Chapter 3 The Wave Equation

the string is

∂

∂x

∂

∂t

, 0 < x < a, 0 < t, (7)

u(0, t) = 0, u(a, t) = 0, 0 < t, (8)

u(x, 0) = f (x), 0 < x < a, (9)

∂u

∂t

(x, 0) = g(x), 0 < x < a, (10)

under the assumptions noted plus the assumption that gravity is negligible.

EXERCISES

1. Find the dimensions of each of the following quantities, using the facts that

force is equivalent to mL/t

, and that the dimension of tension is F (force):

u, ∂

u/∂x

, ∂

u/∂t

, c, g/c

. Check the dimension of each term in Eq. (5).

2. Suppose a distributed vertical force F(x, t) (positive upwards) acts on the

string. Derive the equation of motion:

∂

∂x

∂

∂t

−

F(x, t).

The dimension of a distributed force is F/L. (If the weight of the string is

considered as a distributed force and is the only one, then we would have

F(x, t) =−ρg. Check dimensions and signs.)

3. Find a solution v(x) of Eq. (5) with boundary conditions Eq. (8) that is

independent of time. (This corresponds to a “steady-state solution,” but

the term steady-state is no longer appropriate. Equilibrium solution is more

accurate.)

4. Suppose that the string is located in a medium that resists its movement,

such as air. The resistance is expressed as a force opposite in direction and

proportional in magnitude to velocity. Thus it affects only Eq. (2). Proceed

to derive the equation that replaces Eq. (7) for this case.

3.2 Solution of the Vibrating String Problem

The initial value–boundary value problem that describes the displacement of

the vibrating string,

3.2 Solution of the Vibrating String Problem 219

∂

∂x

∂

∂t

, 0 < x < a, 0 < t, (1)

u(0, t) = 0, u(a, t) = 0, 0 < t, (2)

u(x, 0) = f (x), 0 < x < a, (3)

∂u

∂t

(x, 0) = g(x), 0 < x < a, (4)

contains a linear, homogeneous partial differential equation and linear, homo-

geneous boundary conditions. Thus we may apply the method of separation of

variables with hope of success. If we assume that

u(x, t) = φ(x)T(t), Eq. (1)

becomes



(x)T(t) =

φ(x)T



(t).

Dividing through by φT,weobtain



(x)

φ(x)



(t)

T(t)

, 0 < x < a, 0 < t.

For the equality to hold, both members of this equation must be constant.

We write the constant as −λ

and separate the preceding equation into two

ordinary differential equations linked by the common parameter λ



+λ

T = 0, 0 < t, (5)



+λ

φ = 0, 0 < x < a. (6)

The boundary conditions become

φ(0)T(t) = 0,φ(a)T(t) = 0, 0 < t

and, since T(t) ≡ 0 gives a trivial solution for u(x, t),wemusthave

φ(0) = 0,φ(a) = 0. (7)

TheeigenvalueproblemEqs.(6)and(7)isexactlythesameastheonewe

have seen and solved before. (See Chapter 2, Section 3.) We know that the

eigenvalues and eigenfunctions are



nπ



,φ

(x) = sin(λ

x), n = 1, 2, 3,....

Equation (5) is also of a familiar type, and its solution is known to be

(t) = a

cos(λ

ct) + b

sin(λ

ct),

T no longer symbolizes tension.

220 Chapter 3 The Wave Equation

where a

and b

arearbitrary.(Inotherwords,therearetwoindependentsolu-

tions.) Note, however, that there is a substantial difference between the T that

arises here and the T that we found in the heat conduction problem. The most

important difference is the behavior as t tends to inﬁnity. In the heat conduc-

tion problem, T(t) tends to 0, whereas here T(t) has no limit but oscillates

periodically in agreement with our intuition.

For each n = 1, 2, 3,...,wenowhaveproductsolutions

(x, t) = sin(λ



cos(λ

ct) +b

sin(λ

ct)



. (8)

Such solutions are called standing waves.Foraparticulara

and b

, u

(x, t)

maintains the same shape with a variable, periodic amplitude. For any choice

of a

and b

, u

(x, t) is a solution of the homogeneous partial differential

equation (1) and also satisﬁes the boundary conditions Eq. (2). Some standing

waves are shown animated on the CD.

By the Principle of Superposition, linear combinations of the u

(x, t) also

satisfy both Eqs. (1) and (2). In making our linear combinations, we need no

new constants because the a

and b

are arbitrary. We have, then,

u(x, t) =

∞



n=1

sin(λ



cos(λ

ct) + b

sin(λ

ct)



. (9)

The initial conditions, which remain to be satisﬁed, have the form

u(x, 0) =

∞



n=1

sin



nπx



=f (x ), 0 < x < a,

∂u

∂t

(x, 0) =

∞



n=1

nπ

c sin



nπx



=g(x), 0 < x < a.

(Here we have assumed that

∂u

∂t

(x, t) =

∞



n=1

sin(λ



−a

c sin(λ

ct) + b

c cos(λ

ct)



In other words, we assume that the series for u may be differentiated term by

term.) Both initial conditions take the form of Fourier series problems: A given

function is to be expanded in a series of sines. In each case, then, the constant

multiplying sin(nπ x /a) must be the Fourier sine coefﬁcient for the given func-

tion. Thus we determine that



f (x) sin



nπx



dx, (10)

3.2 Solution of the Vibrating String Problem 221

and

nπ

c =



g(x) sin



nπx



nπc



g(x) sin



nπx



dx. (11)

If the functions f (x) and g(x) are sectionally smooth on the interval 0 < x <

a, then we know that the initial conditions really are satisﬁed, except possibly

at points of discontinuity of f or g. By the nature of the problem, however, one

would expect that f , at least, would be continuous and would satisfy f (0) =

f (a) = 0. Thus we expect the series for f to converge uniformly.

Example.

If the string is lifted in the middle and then released, appropriate initial condi-

tions are

u(x, 0) = f (x) =











h ·

, 0 < x <



2 −



< x < a,

∂u

∂t

(x, 0) = g(x) ≡ 0, 0 < x < a.

Then b

=0 for n = 1, 2, 3,...,and





a/2

h ·

sin



nπx



dx +



a/2



2 −



sin



nπx





sin(nπ/2)

Therefore the complete solution is

u(x, t) =

∞



n=1

sin(nπ/2)

sin



nπx



cos



nπct



. (12)

The CD shows an animated version of this solution.



Although the solution in the example can be considered valid, it is difﬁcult

to see, in the present form, what shape the string will take at various times.

However, because of the simplicity of the sines and cosines, it is possible to

rewrite the solution in such a way that u(x, t) may be determined without

summing a series.

222 Chapter 3 The Wave Equation

By applying the trigonometric identity

sin(A) cos(B) =



sin(A −B) +sin(A +B)



we can express u(x, t) as

u(x, t) =



∞



n=1

sin(nπ/2)

sin



nπ(x − ct)



∞



n=1

sin(nπ/2)

sin



nπ(x + ct)





We know that the series

∞



n=1

sin(nπ/2)

sin



nπx



actually converges to the odd periodic extension, with period 2a,ofthefunc-

tion f (x). Let us designate this extension by

(x) andnotethatitisdeﬁnedfor

all values of its argument. Using this observation, we can express u(x, t) more

simply as

u(x, t) =



(x −ct) +

(x +ct)



. (13)

In this form, the solution u(x, t) can easily be sketched for various values

of t.Thegraphof

(x +ct) has the same shape as that of

(x) but is shifted ct

units to the left. Similarly, the graph of

(x −ct) is the graph of

(x) shifted

ct units to the right. When the graphs of

(x +ct) and

(x −ct) are drawn on

the same axes, they may be averaged graphically to get the graph of u(x, t).

In Fig. 3 are graphs of

(x +ct),

(x −ct),and

u(x, t) =



(x +ct) +

(x −ct)



for the particular example discussed here and for various values of t.Thedis-

placement u(x, t) is periodic in time, with period 2a/c. During the second

half-period (not shown), the string returns to its initial position through the

positions shown. The horizontal portions of the string have a nonzero veloc-

ity. Equation (12) can also be used to ﬁnd u(x, t) for any given x and t.For

instance, if we take x = 0.2a and t =0.9a/c,weﬁndthat



0.2a, 0.9





(−0.7a) +

(1.1a)





(−0.6h) +(−0.2h)



=−0.4h.

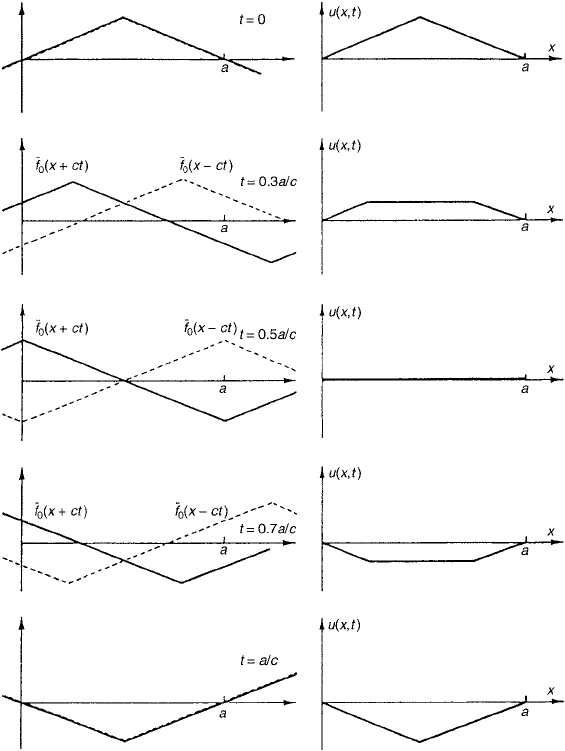
3.2 Solution of the Vibrating String Problem 223

Figure 3 On the left are the graphs of

(x + ct) (solid) and

(x − ct) (dashed)

for the given value of ct. On the right is the graph of u(x, t) for 0 < x < a,made

by averaging the graphs on the left.

The function values can be read directly from a graph of f (x). The manipula-

tions with the series solution in the example can be done for any f (x).There-

fore the formula of Eq. (13) is a solution of Eqs. (1)–(4) for any f (x),provided

that g(x) ≡ 0. We will generalize in later sections.

Frequencies of Vibration

The product solutions in Eq. (8) provide important information about pos-

sible frequencies of vibration. The multipliers λ

c in the sines and cosines of

224 Chapter 3 The Wave Equation

t are frequencies, in radians per unit time; λ

c/2π are frequencies in cycles

per unit time (or Hertz, if the time unit is seconds). For the vibrating string

problem, the possible frequencies of vibration are

(nπ/a)c

2π

πc

The fact that these form an arithmetic sequence guarantees a common period

for all the u

(x, t) in Eq. (8), and thus u(x, t) in Eq. (9) is a function that is

periodic in time.

EXERCISES

1. Verify that the product solution

(x, t) = sin(λ



cos(λ

ct) + b

sin(λ

ct)



satisﬁes the wave equation (1) and the boundary conditions, Eq. (2).

2. Sketch u

(x, t) and u

(x, t) as functions of x for several values of t.Assume

and a

= 1, b

and b

= 0. (The solutions u

(x, t) are called standing

waves.)

In Exercises 3–5, solve the vibrating string problem, Eqs. (1)–(4), with the ini-

tial conditions given.

3. f (x) = 0, g(x) = 1, 0 < x < a.

4. f (x) = sin



πx



, g(x) = 0, 0 < x < a.

5. f (x) =



, 0 < x < a/2,

0, a/2 < x < a,

g(x) = 0, 0 < x < a.

(This initial condition is difﬁcult to justify for a vibrating string, but it

may be reasonable where the unknown function is pressure in a pipe with

a membrane at the midpoint. See Miscellaneous Exercise 18 of this chapter

for some derivations.)

6. If

∞



n=1

sin



nπx



(x),

∞



n=1

cos



nπx



(x),

show that u(x, t) asgiveninEq.(9)maybewritten

3.2 Solution of the Vibrating String Problem 225

u(x, t) =



(x −ct) +

(x +ct)





(x +ct) −

(x −ct)



Here,

(x) and

(x) are periodic with period 2a.

7. The pressure of the air in an organ pipe satisﬁes the equation

∂

∂x

∂

∂t

, 0 < x < a, 0 < t,

with the boundary conditions (p

is atmospheric pressure)

a. p(0, t) = p

, p(a, t) = p

if the pipe is open, or

b. p(0, t) = p

∂p

∂x

(a, t) = 0 if the pipe is closed at x = a.

Find the eigenvalues and eigenfunctions associated with the wave equation

for each of these sets of boundary conditions.

8. Find the lowest frequency of vibration of the air in the organ pipes referred

to in Exercise 7a and b.

9. If a string vibrates in a medium that resists the motion, the problem for

the displacement of the string is

∂

∂x

∂

∂t

∂u

∂t

, 0 < x < a, 0 < t,

u(0, t) = 0, u(a, t) = 0, 0 < t

plus initial conditions. Find eigenfunctions, eigenvalues, and product so-

lutions for this problem. (Assume that k is small and positive.)

10. For the problem in Exercise 9, ﬁnd frequencies of vibration and show that

they do not form an arithmetic sequence. If we form a series solution, will

it be periodic? What happens to u(x, t) as t →∞?

11. The displacements u(x, t) of a uniform thin beam satisfy

∂

∂x

=−

∂

∂t

, 0 < x < a, 0 < t.

If the beam is simply supported at the ends, the boundary conditions are

u(0, t) = 0,

∂

∂x

(0, t) = 0, u(a, t) = 0,

∂

∂x

(a, t) = 0.

Find product solutions to this problem. What are the frequencies of vibra-

tion?

12. Write out formulas for the ﬁrst four frequencies of vibration for a thin

beam (Exercise 11) and for a string (text). Then ﬁnd their values, assum-

ing that parameters c and a have values that make the lowest frequency of

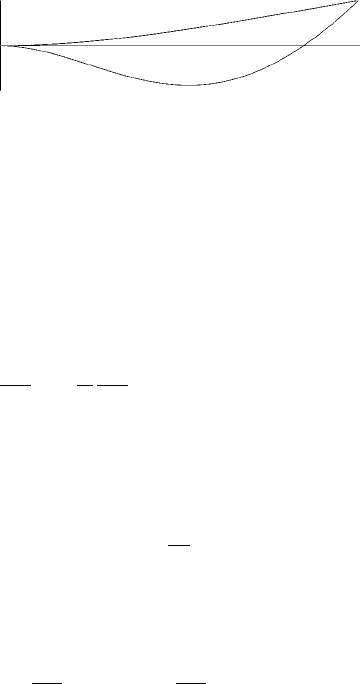
226 Chapter 3 The Wave Equation

Figure 4 Shapes of car antenna.

eachequalto256cyclespersecond.Thedifferenceinthesetoffrequen-

cies accounts for some of the difference between the sound of a stringed

instrument and that of a xylophone or glockenspiel.

13. My car’s antenna vibrates in the wind under various conditions in one of

the two shapes shown in Fig. 4. If the antenna is modeled as a uniform thin

beam with centerline displacement u(x, t),thenu satisﬁes the equation

∂

∂x

=−

∂

∂t

+f (x, t), 0 < x < a, 0 < t,

where f is a “forcing function” that represents the effect of wind or other

distributed forces. Because the base of the antenna is built into the car, the

boundary conditions at the base are zero displacement and slope:

u(0, t) = 0,

∂u

∂x

(0, t) = 0, 0 < t.

The top of the antenna is free to move. There, the internal moment and

shear are both zero, leading to the conditions

∂

∂x

(a, t) = 0,

∂

∂x

(a, t) = 0, 0 < t.

(These four boundary conditions are standard for a cantilevered beam.)

It can be shown that the solution of the foregoing problem, together with

initial conditions on u and u

, can be represented as a series of products

of the form



cos





sin





(t)



(x),

where F

(t) comes from the forcing function and φ

(x) and λ

are related

through the eigenvalue problem



−λ

φ = 0, 0 < x < a,

φ(0) = 0,φ



(0) = 0,φ



(a) =0,φ



(a) =0.

This arises in the obvious way from the boundary conditions and the ho-

mogeneous partial differential equation.

3.3 d’Alembert’s Solution 227

Solve the eigenvalue problem, sketch the ﬁrst two eigenfunctions, and

compare them to the ﬁgure.

In Exercises 14–16, ﬁnd a solution by separation of variables.

14.

∂

∂x



∂

∂t

+2k

∂u

∂t



,0< x < a,0< t,

u(0, t) = 0, u(a, t) = 0, 0 < t,

u(x, 0) = f (x),

∂u

∂t

(x, 0) = 0, 0 < x < a,

where f (x) is as in Eq. (11). (Assume that k is small and positive.)

15.

∂

∂x

∂

∂t

+γ

u,0< x < a,0< t,

u(0, t) = 0, u(a, t) = 0, 0 < t,

u(x, 0) = h,

∂u

∂t

(x, 0) = 0, 0 < x < a,

where h and γ

are constants.

16.

∂

∂x

∂

∂t

,0< x < a,0< t,

u(0, t) = 0,

∂u

∂x

(a, t) = 0, 0 < t,

u(x, 0) = 0,

∂u

∂t

(x, 0) = 1, 0 < x < a.

17. Does the series in Eq. (12) converge uniformly?

18. In the text, we assumed that the ratio φ



/φ had to be a negative con-

stant. Show that, if φ



/φ = p

> 0 (or equivalently, if φ



−p

φ = 0), then

the only function that also satisﬁes the boundary conditions, Eq. (7), is

φ(x) ≡ 0.

3.3 d’Alembert’s Solution

In Section 2 we saw that, in some cases, we could express the solution of the

wave equation directly in terms of the initial data. From this evidence we might

suspect that there is something special about x +ct and x −ct.Totestthisidea,

we change variables and see what the wave equation looks like. Let w =x +ct,

z =x −ct,andu(x, t) = v(w,z). Then a calculation using the chain rule shows

that the wave equation becomes (see Exercise 11)

∂

∂z ∂w

=0.