Пеллинен Л.П. Высшая геодезия (Теоретическая геодезия)
Подождите немного. Документ загружается.



Л.
П. Пелли
высшая
геодезия
(ТЕОРЕТИЧЕСКАЯ ГЕОДЕЗИЯ)
Допущено Министерством высшего и среднего
специального образования СССР в качестве
учебного пособия для студентов вузов,
обучающихся по специальности «Астрономогеодезия)>
МОСКВА «НЕДРА» 1978

УДК
528.2/.3(075.81
Подлинен
Л. П.
Высшая геодезия (Теоретическая геодезия).
М., Недра,
1978. 264 с.
Книга посвящена вопросам определения фигуры
и
гравита-
ционного поля Земли
и
использования полученных данных
при
обработке астрономо-геодезических сетей
и
состоит
из
двух
ча-
стей.
В
первой части х<Астрономо-геодезическйй метод изучения
фигуры Земли» рассмотрены основные понятия астрономо-гео-
дезического метода определения фигуры Земли, редукционная
задача геодезии, теория высот, определение уклонений отвеса
и высот квазигеоида, вопросы оценки точности
и
уравнивания
обширных астрономо-геодезических сетей.
/
Во второй части «Общие исследования фигуры
и
внешнего
гравитационного поля Земли» рассмотрены понятия Нормальной
Земли, фундаментальных геодезических постоянных
и
связанных
с ними систем геодезических координат, изложены методы
и
резу-
льтаты определения фундаментальных геодезических постоян-
ных,
в том
числе метод градусных измерений, современные
результаты определения планетарного геоида, проблемы гео-
динамических исследований.
Книга предназначена
для
студентов астрономо-геодезиче-
ской специальности,
а
также
для
специалистов, занимающихся
вопросами, связанными
с
использованием данных
о
фигуре
и гравитационном поле Земли
и их
изменений
во
времени.
Табл.
19, ил. 73,
список
лит. — 148
назв.
П
11щ
{
^
8
102-79 (g);
Й8яатея1Ш1Ш
•
«Надра»,
1978
ЛБ
№ 3239
ЛЕОНАРД ПАВЛО ВИЧ ПЕЛЛИНЕН
ВЫСШАЯ ГЕОДЕЗИЯ
Редактор издательства
Н. В.
Протопопова
Переплет художника
В. В.
Евдокимова
Художественный редактор
В. В.
Евдокимов
Технический редактор
Л. Г.
Лаврентьева
Корректор T.G. Суворова
Сдано
в
набор
28.02.78.
Подписано
в
печать
12.09.78.
Т-14584 Формат
60 X
90у
1в
.
Бумага
№ 3.
Гарнитура литер. Печать высокая. Печ.
л. 16,5.
Уч.-изд.
л. 16,46.
Тираж
6900 экз.
Заказ
830/5394—15.
Цена
85 коп.
Издательство «Недра»,
103633,
Москва,
К-12,
Третьяковский проезд,
1/19
Ленинградская типография
Ne 6
Союзполиграфпрома
при
Государственном комитете
СССР
по
делам издательств, полиграфии
и
книжной торговли.
196006,
Ленинград, Московский
пр., 91.

ПРЕДИСЛОВИЕ
Курс теоретической геодезии является завершающим в основ-
ном курсе для астрономо-геодезической специальности — высшей
геодезии.
В предлагаемом курсе рассматривается решение основной
научной задачи геодезии — определения фигуры и внешнего
гравитационного поля Земли и их изменений во времени. При этом
наряду с использованием наземных астрономо-геодезических по-
строений, чему уделялось основное внимание в уже изученных
разделах высшей геодезии, будут рассмотрены вопросы исполь-
зования результатов, получаемых другими — физическим (гра-
виметрическим), спутниковыми новейшими космическими — мето-
дами. Многие вопросы использования данных, получаемых ука-
занными методами, обстоятельно излагаются в курсах теории
фигуры Земли и космической геодезии. Поэтому мы не будем
касаться деталей, излагаемых в других курсах, и основное вни-
мание уделим оптимальной комбинации наземных и космических
методов при решении основной научной задачи геодезии. Будет
обращено внимание на успехи в изучении фигуры и гравитацион-
ного поля Земли, достигнутые в результате всех современных
методов, и на перспективы дальнейшего прогресса в этой об-
ласти. ' ~
Первая часть курса — «Астрономб-геодезический метод изу-
чения фигуры Земли» посвящена, главным образом вопросам
математической обработки .астрономо-геодезических сетей как
пространственных построений. Результатом такой математической
обработки является определение фигуры Земли в пределах астро-
номо-геодезической сети в принятой для нее пространственной
геодезической системе координат. Лишь затем, когда студенты
получат представление о возможностях гравиметрического и спут-
никового методов из других курсов, рассматриваются во второй
части курса вопросы определения фигуры и внешнего гравита-
ционного поля Земли в целом в системе координат, связанной
с центром масс Земли.
По сравнению с классическим курсом члена-корреспондента
АН СССР проф. Ф. Н. Красовского «Руководство по высшей
геодезии», ч. II» [46] и хорошо известным «Курсом высшей
1*
з

геодезии» проф. П. С. Закатова [28, 29] автор сделал попытку
изложить в пределах ограниченного объема курса не только тради-
ционные вопросы теоретической геодезии, но и многие новые
вопросы, возникшие в последние годы стремительного развития
геодезии. Автор ясно сознает трудности такого изложения и с боль-
шой признательностью готов принять замечания читателей.
Считаю своим долгом поблагодарить сотрудников кафедры
высшей геодезии МИИГАиК, в особенности доц. А. П. Юзефо-
вича, за внимательное обсуждение рукописи курса и многие цен-
ные замечания, которые были мной учтены при подготовке книги.

ЧАСТЬ ПЕРВАЯ
АСТРОНОМО-ГЕОДЕЗИЧЕСКИЙ МЕТОД
ИЗУЧЕНИЯ ФИГУРЫ ЗЕМЛИ
ГЛАВА I
ВВЕДЕНИЕ
§ 1. ЗАДАЧИ ТЕОРЕТИЧЕСКОЙ ГЕОДЕЗИИ
Под теоретической геодезией будем понимать раздел высшей
геодезии, в котором рассматриваются вопросы решения основной
научной задачи геодезии — определения фигуры и внешнего
гравитационного поля Земли и их изменений во времени —
геодезическими методами. Курс теоретической геодезии имеет
ту же основную направленность, что и курс теории фигуры Земли,
в котором основное внимание уделяется использованию грави-
метрических данных при решении сформулированной задачи.
Понятие фигуры Земли неоднозначно и имеет различную
трактовку в зависимости от использования получаемых данных.
Обычно под действительной фигурой Земли понимают фигуру ее
физической поверхности, на которой проводятся
наземные измерения, т. е. поверхность суши и невозмущенную
поверхность морей, океанов и озер (рис. 1). Следует заметить,
что в задачи высшей геодезии не входит получение непрерывного
представления фигуры физической поверхности Земли, например,
в виде карт. Этим занимаются другие разделы геодезии, аэро-
фотосъемки и картографии. Основную задачу высшей геодезии
формулируют обычно лишь как определение положения
некоторой сети опорных точек в единой
си-стеме пространственных координат. Та-
кая сеть может иногда быть очень редкой (с пунктами через сотни
и тысячи километров в космических геодезических построениях),
но может иметь и такую густоту, которая характеризует класси-
ческие наземные геодезические сети (через несколько километров).
Наряду с фигурой физичебкой поверхности Земли в научных
исследованиях и при решении практических задач немаловажное
значение имеет определение положения фигур уровенных поверх-
ностей реального потенциала силы тяжести. Достаточно напом-
нить,
что горизонтали на топографических картах в первом при-
ближении можно трактовать как линии пересечения таких по-
верхностей с физической поверхностью Земли. Важнейшую роль
играет поверхность геоида, т. е. уровенная поверхность
поля силы тяжести, проходящая через начало отсчета высот. Эта
поверхность близка к невозмущенному среднему уровню океанов
и сообщающихся с ним морей, что часто даже отражают в самом

определении геоида. Однако из-за различия температуры и соле-
ности воды в различных частях Мирового океана и других причин
поверхность геоида строго не совпадает с указанным уровнем
[24, стр. 8—9]. Например, в зоне Панамского канала установлена
разность уровней Тихого и Атлантического океанов в 62 см.
физическая
fl°jf£fe
поверхность Земли
евозмущенная
топографическая
Л
кость
и океанов
Геоид
Рис. 1
До семидесяти сантиметров выше уровня Черного моря и морей,
примыкающих к Северному Ледовитому и Тихому океанам,
располагается нуль-пункт. Кронштадтского футштока [6]. По
некоторым оценкам, отклонение среднего уровня моря от геоида
в открытых частях Мирового океана может достигать 1 м. Это
обстоятельство заставило различать поверхность геоида и так
называемую топографическую поверхность морей и океанов
[137, с.
585-599].
Несмотря на сказанное, традиционное определение фигуры
Земли как фигуры геоида, до сих пор не потеряло своего значения.
Лишь принципиальная неопределимость фигуры геоида под
районами суши, лежащими выше уровня моря, заставила в стро-
гой постановке задачи перейти к определению фигуры ква-
зигеоида — поверхности, однозначно определяемой по на-
земным измерениям, совпадающей с геоидом на морях и океанах
и очень близко подходящей к нему на суше.
Наконец, для научного и практического использования не-
обходима обобщенная достаточно простая математическая аппро-
ксимация фигуры Земли. Из ряда вариантов наиболее удобным
и в то же время имеющим определенный физический смысл пред-
ставлением фигуры Земли оказался земной эллипсо-
ид — эллипсоид вращения, параметры которого подбирают под
условием наилучшего соответствия фигуре геоида (или, более
строго, квазигеоида) либо в пределах всей Земли в целом, и тогда
определяют общеземной эллипсоид, либо в преде-
лах ограниченных ее областей.
Определение внешнего гравитационного поля Земли в сущ-
ности является геофизической задачей так же, как и изучение
магнитного и других физических полей. Однако, учитывая, что
элементы внешнего гравитационного поля Земли геодезисты,
а.

как правило, определяют одновременно
с
параметрами фигуры
Земли
из
обработки одних
и тех же
данных,
а в
дальнейшем
совместно
их
используют, закономерно проблему определения
внешнего гравитационного поля Земли включать
в
формули-
ровку основной научной задачи геодезии.
С развитием новых средств изучения фигуры Земли
и ее
гра-
витационного поля,
с
повышением
их
точности
и
увеличением
возможности достаточно частых повторных измерений
все
большее
значение приобретает кинематический аспект геоде-
зии
—
определение изменений положения точек земной поверх-
ности
и
элементов земного^ гравитационного поля
во
времени.
Уже появился новый раздел
в
науке
о
Земле, лежащий
на
стыке геодезии, геофизики, астрономии
и
океанологии, зани-
мающийся проблемами изучения изменений положения
и
эле-
ментов гравитационного поля Земли
во
времени
и их
интерпре-
тацией
и
получивший название геодинамики.
В
своем
содержании
он
объединяет
два
круга задач геодезии, сформули-
рованных членом-корреспондентом
АН
СССР
М. С.
Молоденским
в
1958 г. [68] и
названных
им
кинематическая гео-
дезия,
о чем мы уже
говорили выше,
и
динамическая
геодезия,
под
которой Молоденский понимает изучение
сил,
являющихся причиной наблюдаемых изменений фигуры
и
грави-
тационного поля Земли.
Развитие геодинамических исследований позволит
в
будущем:
— получать объективные количественные данные
о
процессах
эволюции фигуры
и
гравитационного поля Земли, например,
установить характер
и
скорость движения крупных блоков земной
коры (литосферных плит), выяснить, меняется
ли и
почему гра-
витационное поле Земли,
что
приведет
к
более правильному
пониманию тектонических процессов
и
более эффективному поиску
полезных ископаемых;
— путем изучения движений земной коры
в
сейсмоактивных
районах получать данные
для
более уточненного прогноза сейсми-
ческой опасности,
в том
чибле крупных землетрясений
и
более
медленных деформаций.
— поддерживать высокую точность астрономо-геодезических,
нивелирных
и
гравиметрических сетей путем учета поправок
за изменения координат
и
силы тяжести
во
времени.
Выполненные оценки показывают,
что
геодинамические
ва-
риации большей частью проявляются
на
уровне величин порядка
10-
8
-f-10~
9
в год,
если
при
определении положения точек
на
Земле
за
единицу измерений принять
ее
средний радиус,
при
опре-
делении силы тяжести
— ее
среднее значение
на
поверхности
Земли,
а при
определении направлений
—
один радиан. Таким
образом, речь идет
о
величинах порядка
6 мм — 6 см, от
одного
до десяти микрогал
и 0,0002—0,002".
Исключением являются
некоторые хорошо изученные ^теодинамические процессы сравни-
тельно короткого периода, проявляющиеся
в
колебаниях уровня

моря, в движении полюсов, в приливных деформациях и неравно-
мерности вращения Земли, с которыми приходится считаться
уже на современном уровне точности измерений. Учет других
геодинамических явлений является в основном делом будущего.
В перспективе изучение вариаций пространственных положений
точек земной
Поверхности
и земного гравитационного поля зай-
мет значительное место в основных работах/ проводимых гео-
дезистами [49].
§ 2. ОСНОВНЫЕ ПОНЯТИЯ АСТРОНОМО-ГЕОДЕЗИЧЕСКОГО
МЕТОДА ИЗУЧЕНИЯ ФИГУРЫ И ВНЕШНЕГО
ГРАВИТАЦИОННОГО ПОЛЯ ЗЕМЛИ
В астрономо-геодезическом методе используются различные
виды геодезических измерений — измерения горизонтальных уг-
лов и зенитных расстояний, линейные измерения, геометрическое
нивелирование, а также астрономические определения широт,
долгот и азимутов и, в некоторой мере, при получении небольших
поправочных членов, — гравиметрические данные. Введем ряд
основных понятий, которые окажутся необходимыми в после-
дующем. В большинстве случаев эти понятия уже известны чита-
телю из изучения других разделов высшей геодезии и поэтому
будут даны без выводов.
Референц-эллипсоид
При обработке астрономо-геодезических сетей применяют сис-
темы геодезических координат, связанные с выбранным эллип-
соидом вращения, который называют референц-эллип-
соид о м. Напомним геометрические соотношения для эллип-
соида вращения, которые нам понадобятся в дальнейшем (рис. 2):
а
—
Ь
о а2_&2
а2
—62
где а — сжатие эллипсоида, е — его первый эксцентриситет,
ё — его второй эксцентрисистет, а — большая полуось или
экваториальный радиус, Ъ — малая полуось эллипсоида.
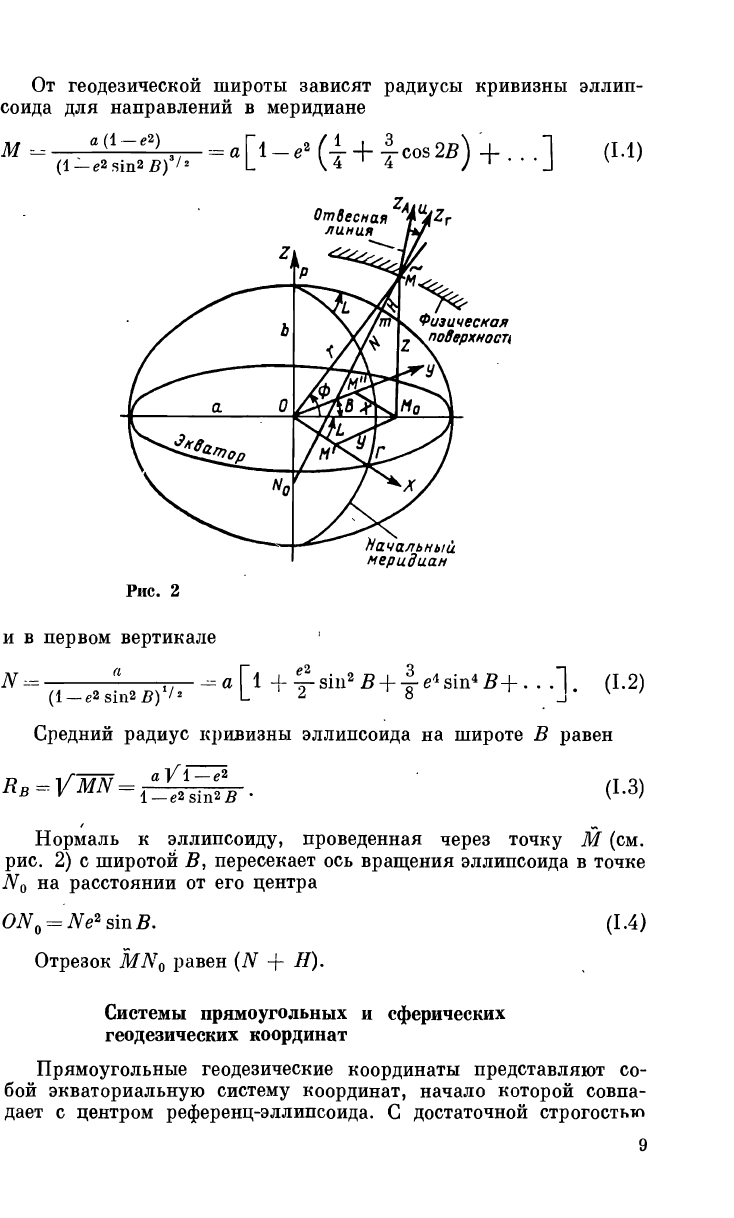
С понятием эллипсоида связаны эллипсоидальные геодези-
ческие координаты (В, L, Н). Согласно рис. 2 для некоторой
точки М, которая лежит в плоскости чертежа, геодезическая
широта В есть угол между нормалью MN
0
к эллипсоиду, прове-
денной через М, и плоскостью экватора; геодезическая долгота
L
— угол между меридиональной плоскостью, проходящей через
точку М, и плоскостью начального меридиана; геодезическая
высота Н — высота точки М над эллипсоидом.
От геодезической широты зависят радиусы кривизны эллип-
соида
для
направлений
в
меридиане
•
меридиан
Рис.
2
и
в
первом вертикале
N
= —^
а
\\
+-fsin
2
5
+
!-e*sin
4
#+.
. Л. (1.2)
(l_
e
2
S
in2
в)
1
* L
1
2
1
8 . -I
Средний радиус кривизны эллипсоида
на
широте
В
равен
RB=vm={j£*
B
,
(i.3)
Нормаль
к
эллипсоиду, проведенная через точку
М
(см.
рис.
2) с
широтой
В,
пересекает
ось
вращения эллипсоида
в
точке
iV
0
на
расстоянии
от его
центра
ON
0
= Ne
2
sin
5. (1.4)
Отрезок
MN
Q
равен
(N + Н).
Системы прямоугольных
и
сферических
геодезических координат
Прямоугольные геодезические координаты представляют
со-
бой экваториальную систему координат, начало которой совпа-
дает
с
центром референц-эллипсоида.
С
достаточной строгостью
