Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials
Подождите немного. Документ загружается.

602
Chapter
7
more and more complex crystal structures are routinely solved and fully
refined using a very basic experimental technique
-
powder diffraction.
Although the utility of the method is somewhat restricted by both the one-
dimensionality of the data and limited instrumental resolution, its power is
astonishing: a simple plot of the observed scattered intensity as a function of
Bragg angle coupled with the computed powder diffraction profile serves as
a sufficient evidence of the correctness of a crystal structure model.
Bragg angle,
20
(deg.)
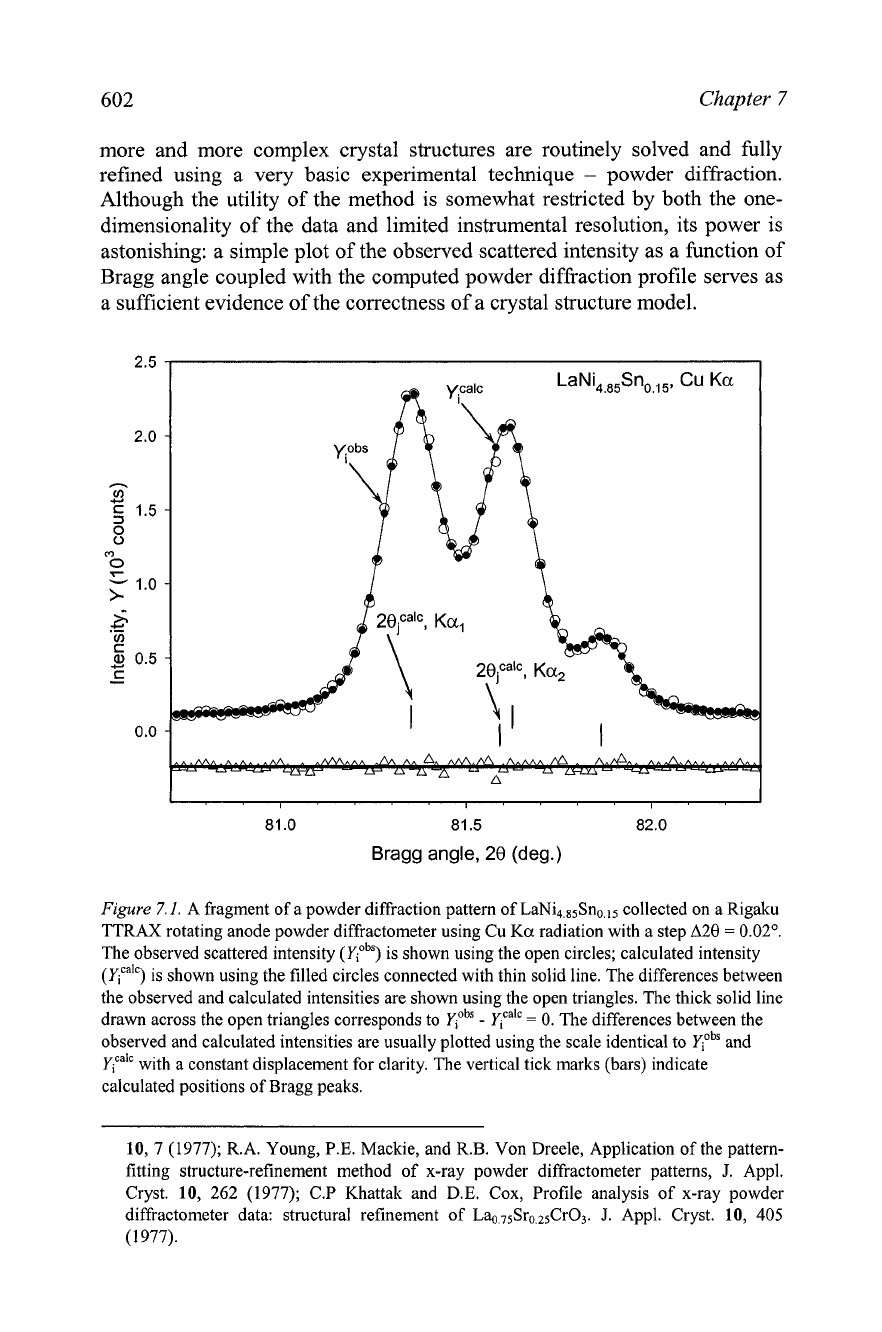
Figure
7.1. A fragment of a powder diffraction pattern of LaNi,,,5Sno,,5 collected on a Rigaku
TTRAX rotating anode powder diffractometer using Cu Ka radiation with a step
A20
=
0.02'.
The observed scattered intensity (yiob") is shown using the open circles; calculated intensity
(yYic) is shown using the filled circles connected with thin solid line. The differences between
the observed and calculated intensities are shown using the open triangles. The thick solid line
drawn across the open triangles corresponds to
5ObS
-
5ca'C
=
0.
The differences between the
observed and calculated intensities are usually plotted using the scale identical to
5ObS
and
yFic with a constant displacement for clarity. The vertical tick marks (bars) indicate
calculated positions of Bragg peaks.
10,
7 (1977); R.A. Young, P.E. Mackie, and R.B. Von Dreele, Application of the pattern-
fitting structure-refinement method of x-ray powder diffractometer patterns,
J.
Appl.
Cryst.
10,
262
(1977); C.P Khattak and D.E. Cox, Profile analysis of x-ray powder
diffractometer data: structural refinement of L%75Sro.25Cr03
J.
Appl. Cryst.
10,
405
(1
977).

Crystal structure refinement
603
No other technique, including a much more sophisticated single crystal
diffraction method, comes close to the Rietveld method in its visual
elegance. Yet when applied properly, the latter competes in accuracy and in
many instances wins easily over the former, especially when a material is
only available in a fine-grained, powdered, untextured thin film or other
states making it out of reach for a single crystal diffraction study
(e.g. see
section 6.17). Furthermore, given several orders of magnitude difference in
specimen size
-
micrograms in single crystal diffraction versus hundreds of
milligrams in powder diffraction
-
the latter is a much better representative
of the materials' structure in the bulk.
It is important, however, to remember that the Rietveld method requires a
model of a crystal structure and by itself offers no clue on how to create such
a model from first principles. Thus, the Rietveld technique is nothing else
than a powerful refinement and optimization tool, which may also be used to
establish structural details (sometimes subtle) that were missed during a
partial or complete
ab initio
structure solution process, i.e. as in the twelve
examples described in Chapter
6.
7.2.1 Rietveld method
basics
During refinement using the Rietveld method, the following system of
equations is solved by means of a non-linear least squares minimization:'
Here
Y?~YS
the observed and Y?'" is the calculated intensity of a point
i
of the powder diffraction pattern,
k
is the pattern scale factor, which is
usually set at
k
=
1 because scattered intensity is measured on a relative scale
and
k
is absorbed by the phase scale factor (e.g. see Eqs. 7.3 and 7.4, below),
and
n
is the total number of the measured data points. Hence, a powder
diffraction pattern in a digital format, in which scattered intensity at every
'
In this section, we are concerned with a powder diffraction experiment, which consists of a
single pattern (profile). The Rietveld technique may also be used to conduct refinement of
the crystal structure employing multiple patterns collected from the same material. For
example, powder diffraction data collected using conventional x-ray sources with different
wavelengths, conventional and synchrotron x-rays, conventional or synchrotron x-rays and
neutron source may be used simultaneously in a combined Rietveld refinement. The
fundamentals of the combined Rietveld refinement are briefly considered in section
7.3.8.

604
Chapter
7
point is measured with high accuracy, is indeed required for a successful
implementation of the technique.
In
the Rietveld method the minimized
function,
@,
is therefore, given by
where
wi
is the weight assigned to the
ith
data point and
k
(Eq.
7.1)
is unity.
The summation in Eq.
7.2
is carried over all measured data points,
n.
Considering Eq.
2.48
and taking into account the one-dimensionality of
powder diffraction data, which introduces multiple Bragg reflection
overlaps, the expanded form of Eq.
7.2
in the simplest case, i.e. when the
powder is a single phase crystalline material, becomes
for a single wavelength experiment or
for dual wavelength
(Kal
+
Ka2)
data.
In
Eqs. 7.3 and 7.4,
bi
is the
background at the
it"
data point,
K
is the phase scale factor,
m
is the number
of Bragg reflections contributing to the intensity of the
it"
data point,
4
is the
integrated intensity of the
jth
Bragg reflection,
yj(xj)
is the peak shape
function,
Axj
is the difference in positions of
Ka,
and
Ka2
components in the
doublet, and
xj
=
28j"alC
-
20i.
A
simple analysis of these two equations indicates that the experimental
minimization of the background, which generally contains little or no useful
In a typical experiment,
n
varies from
-lo3
to
-lo4
data points. In powder diffraction, the
value of
n
is determined only by the scanned Bragg angle range and by the data collection
step,
820:
n
=
(20-
-
20min)/A20
+
1.
It is unrelated to both the complexity of the crystal
structure and the number of Bragg reflections,
M,
which can be observed between
20min
and
20,,.
Obviously,
M
is proportional to the number of symmetrically independent
points in a "visible" fraction of the reciprocal lattice.
A
simple estimate based on the
volumes of the Ewald sphere and the unit cell of a reciprocal lattice, results in
M
cc
vlh3,
where
V
is the volume of the primitive unit cell in direct space and
h
is the wavelength.
Thus, as unit cell volume increases, the number of possible Bragg reflections
(M)
also
increases but the number of observations
(n)
in powder diffraction remains constant,
provided experimental conditions
(h,20,,, 20min,
and
A20)
remain constant.

Crystal structure reJinernent
605
structural information, is of utmost importance for a successful outcome of a
full profile-based refinement. When the background is low, i.e. when
bi
<<
KCIpj(xj), the functions given in both Eqs. 7.3 and 7.4 are defined by
contributions fiom the integrated intensities and peak shape parameters. On
the other hand, when the background is high, i.e. when
bi
E
KCIpj(xj) and,
especially when
bi
>>
KCI/yj(xj), the function, which is minimized during a
least squares refinement, becomes nearly entirely dependent on the adequacy
of the background and not the integrated intensities and peak shapes.
Therefore, a structural model cannot be satisfactory refined using data
collected in the presence of a large background.
In
the absence of a background and assuming that the measured intensity
is only affected by statistical errors (see Eqs. 3.8 and 3.9), the weight can be
given as
obs
-1
wi
=
[T
]
In
practice, the weight is usually calculated without subtracting the
background, which yet again emphasizes the importance to have the latter at
its practical minimum.
When a powder diffraction pattern is collected from a material, which is
a mixture of several
(p)
phases, the contribution from every crystalline phase
is accounted for by modifying Eqs. 7.3 and 7.4 as follows:
Considering Eqs. 7.6 and 7.7, it is clear that each additional crystalline
phase adds multiple Bragg peaks plus a new scale factor along with a set of
corresponding peak shape and structural parameters into the non-linear least
squares. Even though mathematically they are easily accounted for, the finite
accuracy of measurements as well as the limited resolution of even the most
advanced powder diffractometer, usually result in lowering the quality and
stability of the Rietveld refinement in the case of multiple phase samples.
Thus, when the precision of structural parameters is of concern, it is best to
work with single-phase materials, where Eqs. 7.3 and 7.4 are applicable. On
the other hand, since individual scale factors may be independently

606
Chapter
7
determined, Rietveld refinement of multiple-phase powder diffraction
patterns offers an opportunity for a quantitative analysis of a mixture or a
multiple phase crystalline material.'
7.2.2
Classes of Rietveld parameters
Analytical expressions for the background (Eqs. 4.1 to 4.6), integrated
intensity (Eqs. 2.65 to 2.108) and peak shape (Eqs. 2.49 to 2.63) have been
considered earlier, and the minimum of the corresponding function defined
by one of the relevant formulae (Eqs. 7.3 to 7.7) can be found by applying a
non-linear least squares technique (see Eqs. 6.8 to 6.15). Thus, the following
groups of independent least squares parameters are usually refined using the
Rietveld method:
a) 1 to 12 parameters representing the background, although there may be as
many as 36, e.g. in GSAS.
b) Sample displacement, sample transparency or zero-shift corrections.
c) Multiple peak shape function parameters, which usually include full
width at half maximum, asymmetry and other relevant variables, and
depend on the type of a function selected to represent a peak shape.
In
a
multiple phase diffraction pattern, these may be maintained identical or
refined independently for each phase present (generally except for the
asymmetry), if warranted both by the quality of the data and considerable
differences due to the physical state of various phases in the specimen.
d) Unit cell dimensions, usually from
1
to
6
independent parameters for
each crystalline phase present in the specimen.
e) Preferred orientation, and if necessary, absorption, porosity, and
extinction parameters, which usually are independent for each phase.
f)
Scale factors, one for each phase
(KJ,
and in the case of multiple sets of
powder diffraction data, one per pattern excluding the first, which is
fixed at
k
=
1.
g) Positional parameters of all independent atoms in the model of the crystal
structure of each crystalline phase, usually from 0 to 3 per atom.
h) Population parameters, if certain site positions are occupied partially or
by different types of atoms simultaneously, usually one per site.'
i) Atomic displacement parameters, which may be treated as an overall
displacement parameter (one for each phase or a group of atoms) or
'
In this text, we are not specifically concerned with quantitative phase analyses of multiple
phase mixtures, except for a single example considered in section
7.3.8,
below. Interested
reader is referred to an excellent overview given by R.J. Hill, Data collection strategies:
fitting the experiment to the need, in: R.A. Young, Ed., The Rietveld method, Oxford
University Press, Oxford, New York
(1993).
When more than two types of atoms occupy the same site, more than one variable per site
may be adjusted. However, these cases are usually extremely difficult to refine sensibly.
Crystal structure rejnement
607
individual atomic displacement parameters, with the number of
independent variables between one (isotropic approximation) and six
(anisotropic approximation) per site.
The least squares parameters listed in items a) through d) are identical to
those used in
Pawley's and Le Bail's full pattern decompositions, as was
considered in Chapter
6.
Other variables, i.e. those found in items e) through
i) in the list above, are specific to the Rietveld method. Although it is nearly
impossible to prescribe a universal and rigid sequence in which various
groups of physically different parameters should be included in a Rietveld
refinement, Young' suggests the following parameter turn-on sequence
based on their importance and potential for least squares instability:
Table
7.1. A suggested parameter turn-on sequence in a single-phase, single-pattern Rietveld
refinement using constant wavelength x-ray or neutron data (adopted from young).'
Parameter or group of parameters Linear in Stable Comment Sequence
Phase scale Yes Yes a
1
Specimen displacement No Yes b
1
Linear background Yes Yes
c
2
Lattice parameters No Yes d
2
More background Generally no Yes
c
2
or 3
W
No Poorly e 3or5
Coordinates of atoms No Fairly f 3
Preferred orientation No Fairly f
4
or not
Population and isotropic displacements No Varies Correlated
5
U,
V,
other profile parameters No No e Last
Anisotropic displacements No Varies Last
Zero shift No Yes b
1,5ornot
When the scale factor is far off, or when the model of the crystal structure is wrong or too
far from reality, the refined scale factor may become incorrect.
The ~~ecimen~dis~lacement parameter usually varies from sample to sample and it usually
takes up some of the effects of sample transparency. For a properly aligned goniometer,
the zero shift error should be negligible. Even if the goniometer is misaligned, the zero
shift correction should remain sample independent.
When the background is large, at least its constant component should be estimated and
included at the very beginning. In a polynomial approximation, the background parameters
are linear. When more than the required background parameters are employed, severe
correlations may result.
When one or more lattice parameters are incorrect, one or more calculated Bragg peaks can
lock-on to a wrong observed peak, thus leading to a solid false minimum.
U,
V,
W
tend to be highly correlated and various combinations of quite different values can
lead to essentially the same peak widths.
When coordinates of all atoms are refined, the plot of the observed and calculated
diffraction data should be used to determine whether preferred orientation should be
included. Coordinates may strongly correlate in the presence of pseudo-symmetry.
R.A. Young, Introduction to the Rietveld method, in: R.A. Young, Ed., The Rietveld
method, Oxford University Press, Oxford, New York (1993).

608
Chapter
7
The turn-on sequence described in
Table
7.1 may be and often is altered
depending on many variables, which include data quality, accuracy of the
initial structural model, and knowledge of the instrumental contributions to
profile parameters. It is important to realize that rarely, if ever, it is possible
to refine all relevant variables simultaneously from the beginning due to the
complexity of the problem and many possibilities for an out-of-control least
squares. As noted by Young, a systematic, one-by-one turn-on sequence is
nearly always the most effective tool to establish which parameter is causing
the trouble when the refinement does not go well and it is not clear why.
7.2.3
Figures
of
merit and quality
of
refinement
Similar to both Le Bail's and Pawley's full pattern decompositions, the
quality of the refinement using the Rietveld method is quantified by the
corresponding figures of merit: profile residual,
Rp, weighted profile residual
R,,
Bragg residual, RB, expected residual
k,,
and goodness of fit,
x2
(see
Eqs. 6.18 to 6.22). The Durbin-Watson d-statistic (Eqs. 6.23, 6.24) may be
used to quantify a serial correlation between adjacent least squares residuals
in a Rietveld refinement based on step-scan experimental data. As noted
before, all but one
(RB)
residuals depend on both the profile and structural
parameters. The Bragg residual becomes especially significant during
Rietveld refinement because it is the only figure of merit, which is nearly
exclusively dependent on structural parameters and therefore, primarily
characterizes the accuracy of the model of the crystal structure.'
Regardless of the importance of various numerical figures of merit used
to measure the quality of the Rietveld refinement, none of the residuals is a
substitute for the plots of the observed and calculated powder diffraction
patterns supplemented by the difference,
AYi
=
yiobs
-
yicalc, plotted on the
same scale. A standard in the modern representation of the refinement results
also requires inclusion of tick marks indicating the calculated positions of
Bragg peaks
(e.g. see
Figure
6.5 to
Figure
6.11). For dual wavelength data,
Bragg reflections positions calculated for
Ka,
or both
Ka,
and
Ka2
components in the doublet, may be included (e.g. see
Figure
7.1).
'
Bragg residual, Eq. 6.20, as calculated in Rietveld refinement, uses true calculated
integrated intensities but the "observed" integrated intensities are never actually measured
experimentally. They are simply calculated by prorating the observed experimental profile
proportionally to the contributions from multiple overlapped calculated reflection profiles
after the background has been subtracted (see Eq.
6.7), followed by the numerical
integration (see Eq. 2.64). In this regard, Bragg residual also depends on the profile
parameters, although this dependence is far less critical when compared to
Rp,
R,,,
and
X2.
In some references,
RB,
which is based on the square roots of the integrated intensities, is
used as an equivalent of
RE.
The latter employs the absolute values of the observed and
calculated structure factors:
RE
=
c(IKIF~O~~~
-
IF~~~'~~I)/C(KIF~O~~I).

Crystal structure refinement
609
The need for a graphical representation of the results is especially
important because both
R,,
and
R,
absorb the contribution from the
background.
In
extreme cases, when the background is high, it is possible
that the corresponding numerical figures of merit appear to be excellent due
to extremely large denominators in Eqs. 6.18 and 6.19, but neither the model
nor the fit of Bragg peaks make much sense. When the background is
unusually high, both the observed and calculated powder diffraction patterns
should be plotted after a constant component of the background has been
subtracted to enable easy examination of a potential inadequacy of the
selected peak shape function
and/or other unusual discrepancies not visible
on top of a vast background. Truly, the numbers may be biased but the figure
can be trusted when it comes to assessing the quality of Rietveld fits.
7.2.4
Termination of Rietveld refinement
Non-linear least squares technique results in finding a set of increments
that are added to a set of free variables chosen to represent a certain initial
approximation. Parameters, obtained in this ways, are carried over into the
next refinement cycle as a more precise initial approximation.
In
some cases
it may take a few refinement cycles to achieve the best fit, i.e, to minimize
the corresponding function, while in many instances the number of required
least squares steps may be quite large. Especially in Rietveld refinement,
where various groups of parameters have a different and often unrelated
physical origin, the ability to detect the completion of the minimization,
i.e.
the complete convergence of the least squares, is essential.
The critical variables to watch during the refinement are indeed, a set of
standard figures of merit (FOM's), i.e. R,,, R,, RB and
X2.
When the
Rietveld algorithm is stable, they should gradually decrease and then level
off showing minimal fluctuations about certain minimum values, which are
experiment- and structure-specific.
In
some cases, FOM's may begin to rise.
More often than not, their steady or erratic rise indicates the undesired
divergence of the non-linear least squares, which is usually associated with
severe correlations between two or more variables. If this condition is
detected, the refinement should be stopped without saving the results and the
array of free variables re-analyzed to introduce proper constraints.
Even if the refinement is stable, it should be terminated at a certain point.
Because of the finite accuracy of both the data and computations, it is
unrealistic to wait until increments of all least squares parameters become
zero. The latter usually never happens anyway due to simplifications
introduced in the non-linear least squares algorithm (see Eq. 6.9 in section
6.6).
In
addition to the stabilization of all figures of merit near their
respective minima, another important factor that should be considered is the

610 Chapter
7
relationships between the increments and corresponding standard deviations
after each least squares cycle. It is commonly accepted that when all
residuals converge and stabilize at their minima, and when the absolute
values of all increments become smaller than the estimated standard
deviations of the corresponding free variables,' the least squares refinement
may be considered converged (indeed, the model must remain rational).
7.3
Rietveld refinement
of
LaNi4.85Sn0.152
We have seen this powder diffraction pattern several times throughout
this text. The histogram collected from the nearly spherical LaNi4,s5Sno.15
powder, produced by high pressure gas atomization from a melt, was used to
illustrate both the quality of x-ray diffraction data and as one of the examples
in the ab initio crystal structure solution. To demonstrate the Rietveld
refinement of this crystal structure we will begin with the profile and unit
cell parameters determined from Le Bail's algorithm (Table
6.3)
and the
model of the crystal structure determined from sequential Fourier maps as
described in section 6.9 and listed in Table
6.8.
To account for the presumably statistical distribution of Ni and Sn atoms
in the 2(c) and 3(g) sites in this crystal structure, the initial distribution of
atoms in the unit cell has been assumed as listed in Table
7.2.
The initial
profile and structural parameters are found in the input file for LHPM-
Rietica on the CD, the file name is
Ch7ExOla.inp.
Experimental diffraction
data, collected on a Rigaku
TTRAX
rotating anode powder diffractometer
using Cu
Ka
radiation in a continuous scan mode, are located on the CD in
the file
Ch7ExOl-CuKa.dat.
The last column in Table
7.2
contains site occupancies by all atoms in the
format required by LHPM-Rieti~a.~ The occupancy of each site (n) is given
as a product of the population parameter (g) and site multiplicity
(m)
divided
by the multiplicity of the general site position
(M):
The fractional population parameter, g, varies from 1 (fully occupied site)
to 0 (completely unoccupied site). Thus, the fully occupied l(a) site has
occupancy by La:
n
=
1/24
=
0.04167; the 97% occupancy of 2(c) and 3(g)
sites by Ni results in n~il
=
0.97x2/24
=
0.08083 and n~n
=
0.97~3124
=
'
Usually lower than a small (e.g.
1110'~)
fraction of the standard deviation.
J.
Ting,
I.E.
Anderson, and
V.K.
Pecharsky, unpublished.
Some software products, e.g. GSAS, require specification of the population parameters as
g,
while the multiplicities of site positions are automatically included
by
the program.
Crystal structure refinement
61 1
0.12125, respectively. The
3%
occupancy of the same two sites by Sn yields
nsnl
=
0.00250 and
nsn2
=
0.00375, respectively. The overall atomic
displacement parameter,
B
=
0.5
A2,
has been assumed at the beginning of
Rietveld refinement. The progression of the refinement using LHPM-Rietica
is illustrated in
Table
7.3 and in
Figure
7.2
to
Figure
7.5.
Table
7.2. Coordinates of atoms
(x,
y,
and
z)
and site occupancies (n) in the unit cell of
LaNi4,85Sno.15 according to the initial model of the crystal structure (compare with
Table
6.8).
Atom
Site
x
Y
z
n
La
l(4 0
0
0
0.04167
Table
7.3. The progress of Rietveld refinement of the crystal structure of LaNi4,85Sno,15 using
powder diffraction data. Wavelengths used: hKal
=
1.54059
8,
hKal
=
1.54441
8.
In this
and all other tables, the
R,,
RwD, and RB are listed in percent;
X2
is dimensionless.
Refined parameters
R,,
Rw, RB
2
Initial residuals: peak shape, background, zero shift and
unit cell taken from
Table
6.3, initial model fiom
Table
7.2;
see
Figure
7.2
Scale factor
Scale factor, peak shape parameters, background (third
order polynomial), zero shift, unit cell; see
Figure
7.3
All of the above plus overall atomic displacement
parameter
Individual atomic displacement parameters in isotropic
approximation plus all peak shape parameters, background,
zero shift, unit cell, scale
Overall atomic displacement parameter but individual
population parameters of
2(c) and 3(g) sites plus peak
shape parameters, background, zero shift, unit cell, scale
Individual atomic displacement parameters in isotropic
approximation plus all peak shape parameters, background,
zero shift, unit cell, scale
Individual atomic displacement parameters in anisotropic
approximation plus all peak shape parameters, background,
zero shift, unit cell, scale
(i.e. all free variables)
Same as above plus a second phase (as Le Bail's
extraction)
-
i.e. all free variables including those of an
impurity phase; see
Figure
7.5
7.3.1
Scale factor and profile parameters
Initial residuals (row one in
Table
7.3), calculated using profile
parameters determined fiom the full pattern decomposition employing Le
Bail's algorithm and the default value of the scale factor
(K
=
0.01), are quite
