Норенков И.П. Автоматизированное проектирование

Подождите немного. Документ загружается.

%!#*%!#&F*:,$* $I*:+*

F*)&* !)!@&'! +($*,#)KH (*L*)&M

5@!"! 3

∞

Так как

∑

= 1, то

i=0

∞

= 1 -

∑

= 1 - P

(a + a

+ a

+ ...) = 1 / (1 + a + a

+ a

+...) = 1 - a.

i=0

Теперь нетрудно получить и остальные требуемые результаты:

∞

∑

k = P

+ 2P

+ 3P

+... = a (1-a) (1 + 2a + 3a

+...) = a (1-a) / (1-a)

= a / (1-a).

k=1

∞

= P

+ 2P

+ 3P

+... =

∑

(k-1)P

= P

( 1 + 2a + 3a

+...) = a

/ (1-a).

k=2

Времена пребывания в системе и очереди находятся из соотношений:

= λT

которые называют формулами Литтла:

= a / (1-a) / λ = 1 / (µ - λ),

= a

/ (1-a) / λ = a / (µ - λ).

!/+-

:=+4004. /45.D+849:0+. *E$. Для представления имитационных моделей можно ис-

пользовать языки программирования общего применения, однако такие представления оказываются

довольно громоздкими. Поэтому обычно применяют специальные языки имитационного моделирова-

ния на системном уровне. Среди языков имитационного моделирования различают языки, ориентиро-

ванные на описание событий, средств обслуживания или маршрутов движения заявок (процессов).

Выбор языка моделирования определяет структуру модели и методику ее построения.

Ориентация на устройства характерна для функционально-логического и более детальных ие-

рархических уровней описания объектов.

Для описания имитационных моделей на системном уровне (такие модели иногда называют +$-

&$(./' '/'&)='#**./' /#-$49/' — СИМ) чаще используют языки, ориентированные на события

или процессы. Примерами первых могут служить языки Симскрипт, SMPL и ряд других. К числу вто-

рых относятся языки Симула, SOL, а также популярный язык GPSS.

Языки имитационного моделирования реализуются в программно-методических комплексах мо-

делирования СМО, имеющих ту или иную степень специализации. Так, комплексы на базе языка

GPSS можно использовать во многих приложениях, но есть специализированные комплексы для мо-

делирования вычислительных сетей, систем управления предприятиями и т.п.

При использовании языков, ориентированных на процессы, в составе СИМ выделяются элемен-

тарные части и ими могут быть источники входных потоков заявок, устройства, накопители и узлы.

D+&#1*'% (,#-*#8# 0#&#%) 6)9(#% представляет собой алгоритм, в соответствии с которым вычисля-

ются моменты t

появления заявок на выходе источника. Источники могут быть зависимыми и неза-

висимыми. В зависимых источниках моменты появления заявок связаны с наступлением определен-

ных событий, например, с приходом другой заявки на вход некоторого устройства. Типичным неза-

висимым источником является алгоритм выработки значений t

случайной величины с заданным за-

коном распределения.

Q+&"#;+&() в имитационной модели представлены алгоритмами выработки значений интерва-

лов (длительно стей) обслуживания. Чаще всего это алгоритмы генерации значений случайных вели-

чин с заданным законом распределения. Но могут быть устройства с детерминированным временем

обслуживания или временем, определяемым событиями в других частях СИМ. Модель устройства

отображает также заданную дисциплину обслуживания, поскольку в модель входит алгоритм, управ-

ляющий очередями на входах устройства.

G)%#0'&$4' моделируются алгоритмами определения объемов памяти, занимаемых заявками,

приходящими на вход накопителя. Обычно объем памяти, занимаемый заявкой, вычисляется как зна-

&.+.)$(*),$". !"#$%!#&'&($"!))$* +($*,#&($"!)&*

%!#*%!#&F*:,$* $I*:+*

F*)&* !)!@&'! +($*,#)KH (*L*)&M

5@!"! 3

чение случайной величины, закон и (или) числовые характеристики распределения может зависеть от

типа заявки.

Q64. выполняют связующие, управляющие и вспомогательные функции в имитационной моде-

ли, например, для выбора направлений движения заявок в СИМ, изменения их параметров и приори-

тета, разделения заявок на части, их объединения и т.п.

Обычно каждому типу элементарной модели, за исключением лишь некоторых узлов, в про-

граммной системе соответствует определенная процедура (подпрограмма). Тогда СИМ можно пред-

ставить как алгоритм, состоящий из упорядоченных обращений к этим процедурам, отражающим по-

ведение моделируемой системы.

В процессе моделирования происходят изменения модельного времени, которое чаще всего при -

нимается дискретным, измеряемым в тактах. Время изменяется после того, как закончена имитация

очередной группы событий, относящихся к текущему моменту времени t

. Имитация сопровождается

накоплением в отдельном файле статистики таких данных, как количества заявок, вышедших из сис-

темы обслуженными и необслуженными, суммарное время занятого состояния для каждого из уст-

ройств, средние длины очередей и т.п. Имитация заканчивается, когда текущее время превысит задан-

ный отрезок времени или когда входные источники выработают заданное число заявок. После этого

производят обработку накопленных в файле статистики данных, что позволяет получить значения

требуемых выходных параметров.

*4B1-+2012 /.-

45 /45.D+849:0+>. В программах имитационного моделирования СМО пре-

имущественно реализуется +#2.&';*.; /$&#- организации вычислений. Сущность событийного ме-

тода заключается в отслеживании на модели последовательности событий в том же порядке, в как ом

они происходили бы в реальной системе. Вычисления выполняют только для тех моментов времени и

тех частей (процедур) модели, к которым относятся совершаемые события. Другими словами, обра-

щения на очередном такте моделируемого времени осуществляются только к моделям тех элементов

(устройств, накопителей), на входах которых в этом такте произошли изменения. Поскольку измене-

ния состояний в каждом такте обычно наблюдаются лишь у малой доли ОА, событийный метод мо-

жет существенно ускорить моделирование по сравнению с инкрементным методом, в котором на каж-

дом такте анализируются состояния всех элементов модели.

Рассмотрим возможную схему реализации событийного метода имитационного моделирования.

Моделиров ание начинается с просмотра операторов генерирования заявок, т.е. с обращения к мо-

делям источников входных потоков. Для каждого независимого источника такое обращение позволяет

рассчитать мо мент генерации первой заявки. Этот момент вместе с именем — ссылкой на заявку — за-

носится в список будущих событий (СБС), а сведения о генерируемой заявке — в список заявок (СЗ).

Запись в СЗ включает в себя имя заявки, значения ее параметров (атрибутов), место, занимаемое в дан-

ный момент в СИМ. В СБС события упорядочиваются по увеличению моментов наступления.

Затем из СБС выбирают совокупность сведений о событиях, относящихся к наиболее раннему

моменту времени. Эта совокупность переносится в список текущих событий (СТС), из которого из-

влекаются ссылки на события. Обращение по ссылке к СЗ позволяет установить место в СИМ заявки

А, с которой связано моделируемое собы-

тие. Пусть этим местом является устройство

Х. Далее программа моделирования выпол-

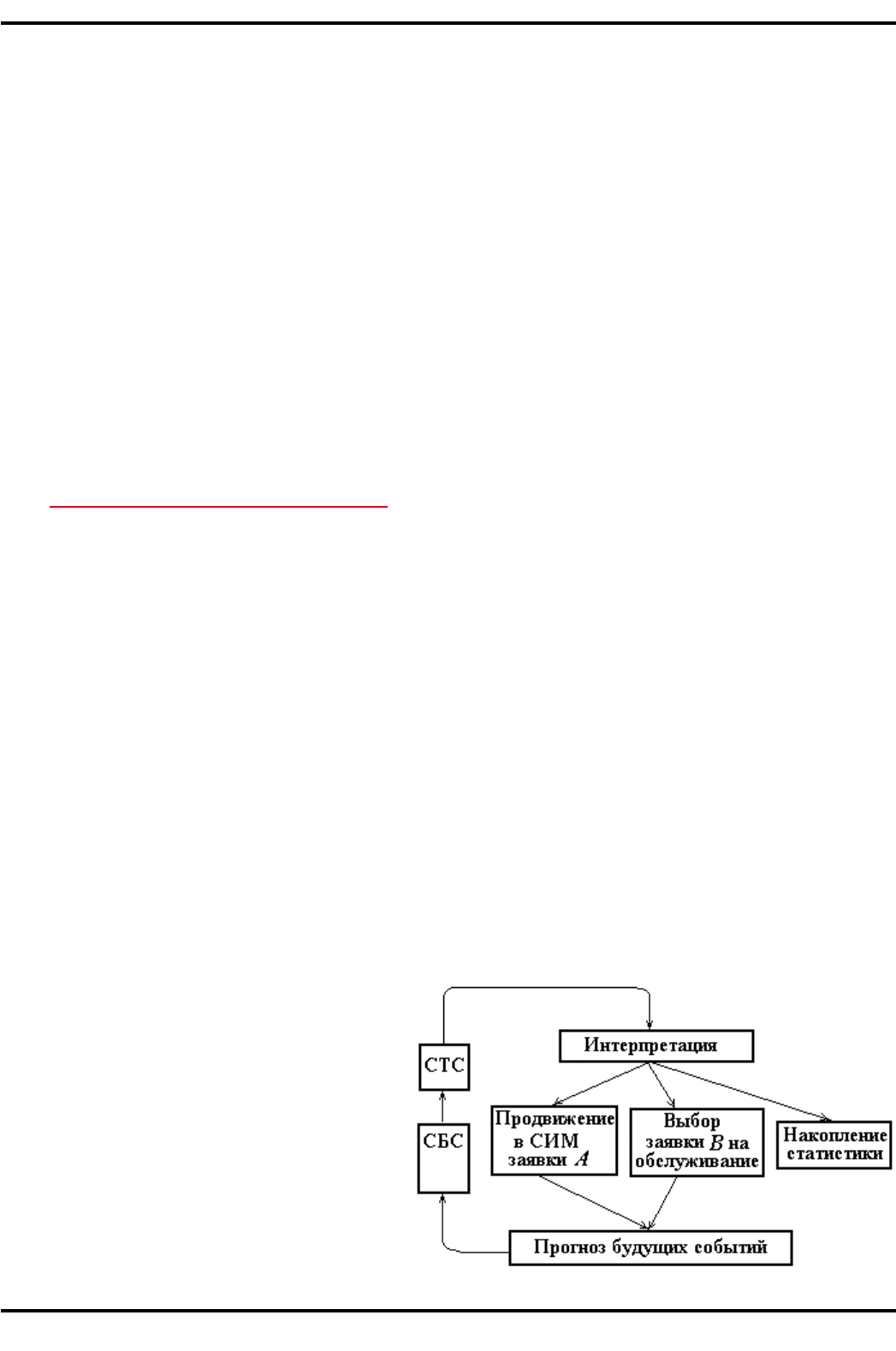
няет следующие действия ( рис. 3.19):

1) изменяет парамет ры состояния уст-

ройства Х; например, если заявка А осво-

бождает Х, а очередь к Х не была пуста, то в

соответствии с заданной дисциплиной об-

служивания из очереди к Х выбирается заяв-

ка В и поступает на обслуживание в Х;

2) прогнозируется время наступления

следующего события, связанного с заявкой

В, путем обращения к модели устройства Х,

&.+.)$(*),$". !"#$%!#&'&($"!))$* +($*,#&($"!)&*

%+,. 3.)9. Иллюстрация событийного моделирования

МАТЕМАТИчЕСКОЕ ОБЕСПЕ

чЕНИЕ АНАЛИЗА ПРОЕКТНЫХ РЕШЕНИЙ

ГЛАВА 3

в которой рассчитывается продолжительность обслуживания заявки В; сведения об этом будущем со-

бытии заносятся в СБС и СЗ;

3) происходит имитация движения заявки А в СИМ по маршруту, определяемому заданной про-

граммой моделирования, до тех пор, пока заявка не придет на вход некоторого ОА; здесь либо заявка

задерживается в очереди, либо путем обращения к модели этого ОА прогнозируется наступление не-

которого будущего события, связанного с дальнейшей судьбой заявки А; сведения об этом будущем

событии также заносятся в СБС и СЗ;

4) в файл статистики добавляются необходимые данные.

После отработки всех событий, относящихся к моменту времени t

, происходит увеличение мо-

дельного времени до значения, соответствующего ближайшему будущему событию, и рассмотренный

процесс имитации повторяется.

Кра

ткое описание языка GPSS. Язык GPSS (General Purpose Simulation System), ориентированный на про-

це ссы, реализован в ряде программ имитационного моделирования. Модель (программа) на языке GPSS представляет со-

бой последовательность операторов ( их называют блоками), отображающих события, происходящие в СМО при переме-

щениях транзактов. Поскольку в интерпретаторах GPSS реализуется событийный метод, и в СМО может быть одновре-

менно много транзактов, то интерпретатор будет попеременно исполнять разные фрагменты программы, имитируя про-

движения транзактов в текущий момент времени до их задержки в некоторых устройствах или очередях.

Операторы GPSS имеют следующий формат:

<метка> <имя оператора> <поле операндов> [<комментарий>]

причем метка может занимать позиции, начиная со второй, имя оператора — с восьмой, поле операндов — с девятнадца-

той, комментарий обязательно отделяется от поля операндов пробелом.

Поле операндов может быть пусто, иметь один или более операндов, обозначаемых ниже при описании блоков сим-

волами А, B, C,... Операндами могут быть идентификаторы устройств, накопителей, служебные слова и стандартные чис-

ловые атрибуты (СЧА). К СЧА относят ся величины, часто встречающиеся в разных задачах. Это, например, АС1 — теку-

щее время, FN — функция, P — параметр транзакта (каждый транзакт может иметь не более L параметров, обычно L =12),

K — констант а, RN1 — случайная величина, равномерно распределенная в диапазоне [0, 1], S — объем занятой памяти в

накопителе, F — состояние устройства, Q — текущая длина очереди и др. При этом ссылки на идентификаторы записы-

ваются в виде

<СЧА>$<идентификатор>

например, Q$ORD означает очередь ORD или FN$COS — ссылка на функцию COS.

Рассмотрим наиболее часто встречающиеся операторы, сопровождая знак омство с ними простыми примерами моделей.

Источники заявок обычно описываются блоком

GENERATE A,B,C,D,E

где А и В служат для задания интервалов между появлениями заявок, при этом можно использовать один из следующих

вариантов: 1) интервал — равномерно распределенная в диапазоне [А-В, А+В] случайная величина; 2) интервал — значе-

ние функции, указанной в В, умноженной на А; С — задержка в выработке первого транзакта; D — число вырабатывае-

мых источником заявок; Е — приоритет заявок. Если D пусто, то число вырабатываемых транзактов неограничено. На-

пример:

GENERATE 6,FN$EXP,,15

Этот оператор описывает источник, который вырабатывает 15 транзактов с интервалами, равными произведению числа 6

и значения функции EXP;

GENERATE 36,12

Здесь число транзактов неограничено, интервалы между транзактами — случайные числа в диапазоне [24, 48].

Функции, на которые имеются ссылки в операторах должны быть описаны с помощью блока следующего типа

M FUNCTION A,B

за которым следует строка, начинающаяся с первой позиции

И.П.НОРЕНКОВ. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ

%!#*%!#&F*:,$* $I*:+*

F*)&* !)!@&'! +($*,#)KH (*L*)&M

5@!"! 3

/..../X

Здесь метка M — идентификатор функции, A — аргумент функции, B — тип функции, X

и Y

— координаты узловых то-

чек функции, заданной таблично. Например:

EXP FUNCTION RN0,C02

0,0/0.2,0.22/0.4,0.50/0.5,0.6/0.6,0.92/... и т.д.

Это описание непрерывной (С) функции EXP, заданной таблично 12-ю узловыми точками, аргументом является случай-

ная величина (RN1), равномерно распределенная в диапазоне [0, 1]; или

DDD FUNCTION *4,D6

0,2/2,5/3,00/4,20/5,08/6,02/7,9

Дискретная (D) функция ВВВ задана 6-ю узловыми точками, аргумент — четвертый параметр транзакта, возбудивший об-

ращение к функции ВВВ.

Тразакты могут порождаться и оператором размножения

SPLIT A,B,C

когда в него входит некоторый транзакт. При этом создается семейство транзактов, включающее основной (вошедший в

блок) транзакт и А его копий. Основной транзакт переходит в следующий по порядку блок, а его копии переходят в блок

с меткой В. Для различения транзактов параметр С основного транзакта увеличивается на 1, а транзактов-копий — на 2,

3, 4,... и т.д.

Обратное действие — сборка транзактов выполняется операторами

ASSEMBLE A

согласно которому первый из вошедших в блок транзактов выйдет из него только после того, как в этот блок придут еще

А-1 транзактов того же семейства, или оператором

GATHER A

отличающимся от предыдущего оператора тем, что из блока выходят все А транзактов.

Оператор

SEIZE A

описывает занятие устройства А транзактом, а оператор

RELEASE A

освобождение устройства А от обслуживания.

Задержка в движении транзакта по СМО описывается оператором

ADVANCE A,B

где А и В имеют тот же смысл, что и в операторе GENERATE.

+-0B.- 7.

Обслуживание транзакта в устройстве WST продолжительностью a единиц времени, где a — равно-

мерно распределенная в диапазоне [7,11] случайная величина, описывается следующим фрагментом программы

...

SEIZE WST

ADVANCE 9,2

RELEASE WST

...

Аналогично описывается занятие транзактом памяти в накопителе

ENTER A,B

&.+.)$(*),$". !"#$%!#&'&($"!))$* +($*,#&($"!)&*

%!#*%!#&F*:,$* $I*:+*

F*)&* !)!@&'! +($*,#)KH (*L*)&M

5@!"! 3

за исключением того, что здесь помимо имени накопителя (А) указывается объем занимаемой памяти (В). Освобождение

В ячеек памяти в накопителе А выполняется оператором

LEAVE A,B

Для накопителей в модели нужно задавать общий объем памяти, что делается в следующем описании накопителя

M STORAGE A

где М — имя накопителя, А — объем памяти.

Если транзакт приходит на вход занятого устройства или на вход накопителя с недостаточным объемом свободной

памяти, то он задерживается в очереди к этому устройству или накопителю. Слежение за состоянием устройств и очере-

дей выполняет интерпретатор. Но если в модели требуется ссылаться на длину очереди или собирать ст атистику по ее дли-

не, то нужно явное указание этой очереди в модели. Делается это с помощью операторов входа в очередь

QUEUE A

и выхода из очереди

DEPART A

согласно которым очередь А увеличивается и уменьшается на единицу соответственно.

Движение транзактов выполняется в естественном порядке, изменение этого порядка производится операторами

перехода. Оператор условного перехода

TEST XX A,B,C

В соответствии с которым переход к оператору, помеченному меткой С, происходит, если не выполняется условие А ХХ

В, где ХХ О {E,NE,L,LE,G,GE}, E- равно, NE — неравно, L — меньше, LE — меньше или равно, G — больше, GE — боль-

ше или равно (XX размещается в позициях 13 и 14).

+-0B.- 2.

Приходящие пользователи ожидают обслуживания, если длина очереди не более 4, иначе от обслу-

живания отказываются. Соответствующий фрагмент программы

...

TEST LE Q$STR,K4,LBL

QUEUE STR

SEIZE POINT

DEPART STR

ADVANCE 50,06

RELEASE POINT

...

LBL TERMINATE 0

...

В примере 2 использован оператор выхода т ранзактов из СМО

TERMINATE A

согласно которому из итогового счетчика вычитается число А.

С помощью итогового счетчика задается длительность моделирования. В начале исполнения программы в счетчик

заносится число, указанное в операнде А оператора

START A,,C

Моделирование прекращается, когда содержимое счетчика будет равно или меньше нуля. Операнд С — шаг выво-

да статистики на печать.

+-0B.- 3.

Общая структура программы на GPSS имеет вид

SIMULATE

<описания, в том числе функций и накопителей >

<операторы, моделирующие движение транзактов>

&.+.)$(*),$". !"#$%!#&'&($"!))$* +($*,#&($"!)&*

%!#*%!#&F*:,$* $I*:+*

F*)&* !)!@&'! +($*,#)KH (*L*)&M

5@!"! 3

START A,,C

END.

Оператор безусловного перехода

TRANSFER ,B

где В — метка оператора, к которому следует переход.

Используется ряд других разновидностей оператора TRANSFER. Например:

TRANSFER P,B,C

Переход происходит к оператору с меткой, равной сумме значения параметра В транзакта и числа С.

TRANSFER FN,B,C

То же, но вместо параметра транзакта слагаемым является значение функции В.

TRANSFER PICK,B,C

Это оператор равновероятного перехода к операторам, метки которых находятся в интервале [B,C]. Важное место в СМО

занимает переход по вероятности

TRANSFER E,B,C

где А — вероятность перехода к оператору с меткой С, переход к оператору с меткой В будет происходить с вероятно-

стью 1 - А.

+-0B.- 4.

Заказы, поступающие в СМО в случайные моменты времени в диапазоне [20,40], выполняет сначала

бригада WGR1, затем параллельно работают бригады WGR2 и WGR3, каждая над своей частью заказа. Заданы экспонен-

циальные законы для времен выполнения работ бригадами WGR1, WGR2 и WGR3 с интенсивностями 0,05, 0,1 и 0,125 со-

ответственно. Моделирование нужно выполнить на временном отрезке, соответствующем выполнению 1000 заказов.

Программа:

SIMULATE

EXP FUNCTION RN0,C02

0,0/.2,.22//.4,.50/.5,.6/.6,.92/.7,0.2/.8,0.60/.9,2.3/.95,3/.99,4.6/.999,6.9/0,0000

GENERATE 30,00

SEIZE WGR0

ADVANCE 20,FN$EXP

RELEASE WGR0

SPLIT 0,MET0

SEIZE WGR2

ADVANCE 00,FN$EXP

RELEASE WGR2

TRANSFER , MET2

MET0 SEIZE WGR3

ADVANCE 8,FN$EXP

RELEASE WGR3

MET2 ASSEMBLE 2

TERMINATE 0

START 0000,,0000

END

В этом примере использован экспоненциальный закон распределения с плотностью

P(t) = λ exp(-λT),

где λ — интенсивность. Функция распределения экспоненциального закона

F(T) = ∫p(t)dt = 1 - exp(-λT).

Из рис. 3.20 ясно, что поскольку искомыми являются значения b случайной величины ?, то, задавая значение a, как

равномерно распределенной в диапазоне [0,1] случайной величины, по формуле

&.+.)$(*),$". !"#$%!#&'&($"!))$* +($*,#&($"!)&*

%+,. 3.20. Функция

экспоненциального закона

распределения

%!#*%!#&F*:,$* $I*:+*

F*)&* !)!@&'! +($*,#)KH (*L*)&M

5@!"! 3

β = (1/λ) ln(1/(1-α)) (3.47)

находим искомое значение. Именно в соответствии с (3.47) в операторах ADVANCE (см. пример 4) множителями были

значения 1/

λ.

Приведем еще несколько операторов языка GPSS.

Оператор изменения параметров транзактов

ASSIGN A,B

где А — номер парамет ра транзакта, В — присваиваемое ему значение. В операторе

ASSIGN A+,B

параметр А увеличивается на значение В, а в операторе

ASSIGN A-,B

уменьшается. Расширение возможностей управления движением транзактов достигается благодаря таким операторам, как

LOGIC_X A

который при Х = S устанавливает переключа тель А в единичное состояние, а при X= R сбрасывает его в нулевое состояние;

GATE_XX A,B

который при XX = LR и А = 1 или при ХХ = LS и А = 0 передает транзакт оператору с меткой В (или задерживает его в

блоке GATE, если поле В пусто), а при других сочетаниях XX и А — направляет к следующему оператору. Вычислитель-

ный оператор

M VARIABLE A

присваивает переменной с номером М значение арифметического выражения А, например в операторе

3 VARIABLE K206-S$MEM2

переменной номер 3 присваивается разность числа 216 и объема занятой памяти в накопителе MEM2. Оператор синхро-

низации, имеющий, например, вид

LBL MATCH NUMB

задерживает приходящий в него транзакт до тех пор, пока в некоторой другой части модели в сопряженный оператор

NUMB MATCH LBL

не войдет т ранзакт того же семейства.

.-+ ".-8+.

:$&' !$&"' — аппарат для моделирования динамических дискретных систем

(преимущественно асинхронных параллельных процессов). Сеть Петри определяется как четверка

<P,T,I,O>, где % и M — конечные множества позиций и переходов, I и $ — множества входных и вы-

ходных функций. Другими словами, сеть Петри представляет собой двудольный ориентированный

граф, в котором 0#6'='9/ соответствуют вершины, изображаемые кружками, а 0$"$,#-)/ — верши-

ны, изображаемые утолщенными черточками; функциям I соответствуют дуги, направленные от по-

зиций к переходам, а функциям $ — от переходов к позициям.

Как и в системах массового обслуживания, в сетях Петри вводятся объекты двух типов: динами-

ческие — изображаются /$&%)/' (/)"%$")/') внутри позиций и статические — им соответствуют

вершины сети Петри.

Распределение маркеров по позициям называют /)"%'"#(%#;. Маркеры могут перемещаться в

сети. Каждое изменение маркировки называют +#2.&'$/, причем каждое событие связано с опреде-

ленным переходом. Считается, что события происходят мгновенно и разновременно при выполнении

некоторых условий.

&.+.)$(*),$". !"#$%!#&'&($"!))$* +($*,#&($"!)&*

%!#*%!#&F*:,$* $I*:+*

F*)&* !)!@&'! +($*,#)KH (*L*)&M

5@!"! 3

Каждому условию в сети Петри соответствует определенная позиция. Совершению события со-

ответствует +")2)&.()*'$ (возбуждение или запуск) перехода, при котором маркеры из входных по-

зиций этого перехода перемещаются в выходные позиции. Последовательность событий образует мо-

делируемый процесс.

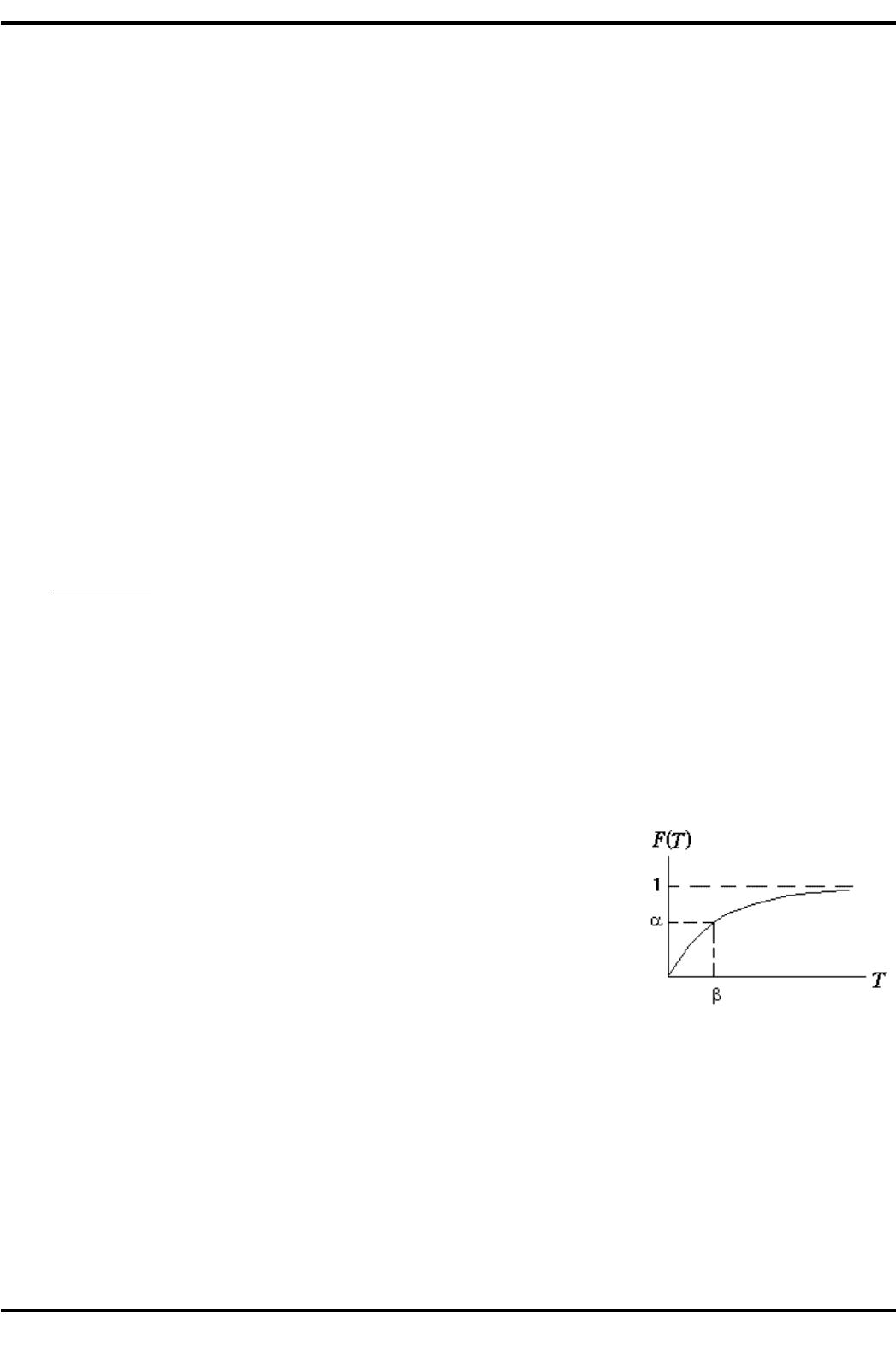
Правила срабатывания переходов (рис. 3.21), конкретизируют сле-

дующим образом: переход срабатывает, если для каждой из его входных

позиций выполняется условие N

X K

, где N

— число маркеров в i-й вход-

ной позиции, K

— число дуг, идущих от i-й позиции к переходу; при сра-

батывании перехода число маркеров в i-й входной позиции уменьшается

на K

, а в j-й выходной позиции увеличивается на M

, где M

— число дуг,

связывающих переход с j-й позицией.

На рис. 3.21 показан пример распределения маркеров по позициям перед срабатыванием, эту

маркировку записывают в виде (2,2,3,1). По сле срабатывания перехода маркировка становится иной:

(1,0,1,4).

Можно вводить ряд дополнительных правил и условий в алгоритмы моделирования, получая ту

или иную разновидность сетей Петри. Так, прежде всего полезно ввести модельное время, чтобы мо-

делировать не только последовательность событий, но и их привязку ко времени. Это осуществляет-

ся приданием переходам веса — продолжительности (задержки) срабатывания, которую можно опре-

делять, используя задаваемый при этом алгоритм. Полученную модель называют ("$/$**#; +$&5<

!$&"'.

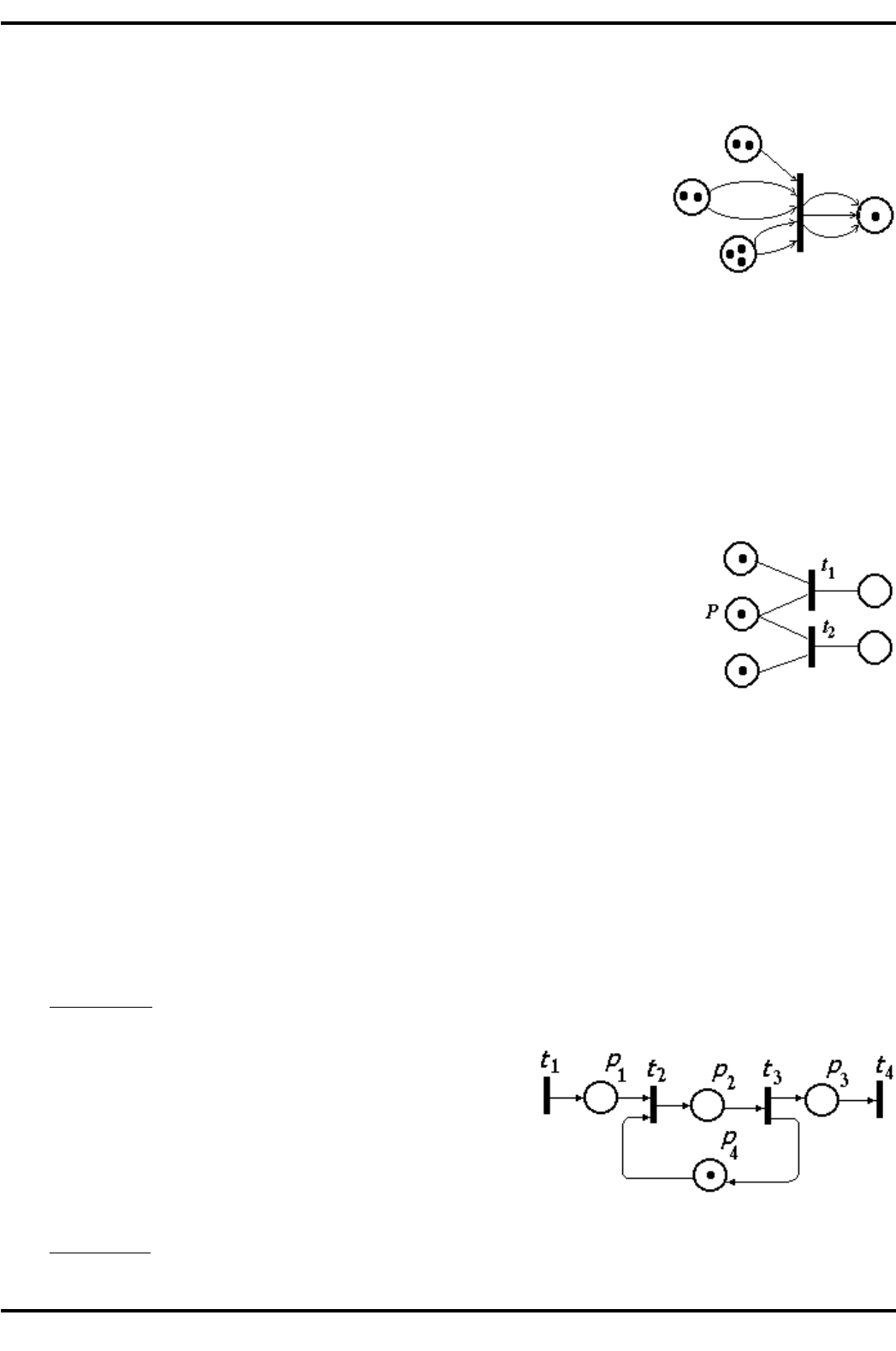
Если задержки являются случайными величинами, то сеть называют

+&#,)+&'1$+%#;. В стохастиче ских сетях возможно введение вероятностей

срабатывания возбужденных переходов. Так, на рис. 3.22 представлен фраг-

мент сети Пет ри, иллюстрирующий конфликтную ситуацию — маркер в по-

зиции p может запустить либо переход t

, либо переход t

. В стохастической

сети предусматривается вероятностный выбор срабатывающего перехода в

таких ситуациях.

Если задержки определяются как функции некоторых аргументов, кото-

рыми могут быть количества маркеров в каких-либо позициях, состояния некоторых переходов и т.п.,

то сеть называют E7*%='#*)45*#;.

Во многих задачах динамиче ские объекты могут быть нескольких типов, и для каждого типа

нужно вводить свои алгоритмы поведения в сети. В этом случае каждый маркер должен иметь хотя

бы один параметр, обозначающий тип маркера. Такой параметр обычно называют цветом; цвет мож-

но использовать как аргумент в функциональных сетях. Сеть Петри при этом называют =($&*#;.

Среди других разновидностей сетей Петри следует упомянуть '*8'2'&#"*.$ сети, характеризу-

ющиеся тем, что в них возможны запрещающие (ингибиторные) дуги. Наличие маркера во входной

позиции, связанной с переходом ингибиторной дугой, означает запрещение срабатывания перехода.

Введенные понятия поясним на следующих примерах.

+-0B.- 7. Требуется опис ать с помощью сети Петри работу группы пользователей на единственной рабочей

станции WS при заданных характеристиках потока запросов на пользование WS и характеристиках поступающих задач.

Сеть Петри представлена на рис. 3.23.

Здесь переходы связаны со следующими событиями: t

— по-

ступление запроса на использование WS, t

— занятие станции, t

—

освобождение станции, t

— выход обслуженной заявки; позиция "

используется для отображения состояния WS: если в "

имеется мет-

ка, то WS свободна и пришедшая заявка вызывает срабатывание пере-

хода t

; пока эта заявка не будет обслужена, метки в "

не будет, следо-

вательно, пришедшие в позицию "

запросы вынуждены ожидать сра-

батывания перехода t

+-0B.- 2.

Требует ся описать с помощью сети Петри процессы возникновения и уст ранения неисправностей в

некоторой технической системе, состоящей из L однотипных блоков; в запасе имеется один исправный блок; известны

статистические данные об интенсивностях возникновения отказов и длительностях таких операций, как поиск неисправ-

&.+.)$(*),$". !"#$%!#&'&($"!))$* +($*,#&($"!)&*

%+,.3.2). Фрагмент сети Петри

%+,.3.22. Конфликтная

ситуация

%+,. 3.23. Сеть Петри для примера 1

%!#*%!#&F*:,$* $I*:+*

F*)&* !)!@&'! +($*,#)KH (*L*)&M

5@!"! 3

но стей, замена и ремонт отказавшего блока. На рис. 3.24

представлена соответствующая сеть Петри. Отметим, что

при числе меток в позиции, равном L, можно в ней не

ставить L точек, а записать в позиции значение L.

В нашем примере значение L в позиции "

соот-

ветствует числу имеющихся в системе блоков. Переходы

отображают следующие события: t

— отказ блока, t

2 —

поиск неисправного блока, t

— его замена, t

— оконча-

ние ремонта.

Очевидно, что при непустой позиции "

переход t

срабатывает, но с задержкой, равной вычисленному слу-

чайному значению моделируемого отрезка времени меж-

ду отказами. После выхода маркера из t

он попадает че-

рез "

в t

, если имеется метка в позиции "

, это означает, что обслуживающая систему бригада специалистов свободна и

может приступить к поиску возникшей неисправности. В переходе t

метка задерживается на время, равное случайному

значению длительно сти поиска неисправности. Далее маркер оказывается в "

и, если имеется запасной блок (маркер в

), то запускается переход t

, из которого маркеры выйдут в "

и в "

через отрезок времени, требуемый для замены

блока. После этого в t

имитируется восстановление неисправного блока.

Рассматриваемая модель описывает функционирование системы в условиях, когда отказы могут возникать и в ра-

бочем, и в неисправном состояниях системы. Поэтому не исключены ситуации, при которых более чем один маркер ока-

жется в позиции "

C0:D+? ,.-.2 ".-8+. Анализ сложных систем на базе сетей Петри можно выполнять посредст-

вом имитационного моделирования СМО, представленных моделями сетей Петри. При этом задают

входные потоки заявок и определяют соответствующую реакцию системы. Выходные параметры

СМО рассчитывают путем обработки накопленного при моделировании статистического материала.

Возможен и другой подход к использованию сетей Петри для анализа объектов, исследуемых на си-

стемном уровне. Он не связан с имитацией процессов и основан на исследовании таких свойств се-

тей Петри, как ограниченность, безопасность, сохраняемость, достижимость, живость.

U8")*'1$**#+&5 (или O-#8")*'1$**#+&5) имеет место, если число меток в любой позиции сети

не может превысить значения O. При проектировании автоматизированных систем определение O

позволяет обоснованно выбирать емкости накопителей. Возможность неограниченного роста числа

меток свидетельствует об опасности неограниченного роста длин очередей.

C$6#0)+*#+&5 — частный случай ограниченности, а именно это 1-ограниченность. Если для не-

которой позиции установлено, что она безопасна, то ее можно представлять одним триггером.

:#,")*9$/#+&5 характеризуется постоянством загрузки ресурсов, т.е.

∑

= const,

где N

— число маркеров в i-й позиции, A

— весовой коэффициент.

N#+&'@'/#+&5 M

→ M

характеризуется возможностью достижения маркировки M

из состо-

яния сети, характеризуемого маркировкой M

Y'(#+&5 сети Петри определяется возможностью срабатывания любого перехода при функцио-

нировании моделируемого объекта. Отсутствие живости означает либо избыточность аппаратуры в

проектируемой системе, либо свидетельствует о возможности возникновения зацикливаний, тупиков,

блокировок.

В основе исследования перечисленных свойств сетей Петри лежит )*)4'6 -#+&'@'/#+&'.

Один из методов анализа достижимости любой маркировки из со стояния E

— построение гра-

фа достижимости. Начальная вершина графа отображает E

, а остальные вершины соответствуют

маркировкам. Дуга из E

в E

означает событие M

→ M

и соответствует срабатыванию перехода t.

В сложных сетях граф может содержать чрезмерно большое число вершин и дуг. Однако при постро-

ении графа можно не отображать все вершины, так как многие из них являются дублями (действи-

тельно, от маркировки M

всегда порождается один и тот же подграф вне зависимости от того. из ка-

кого состояния система пришла в E

). Тупики обнаруживаются по отсутствию разрешенных перехо-

&.+.)$(*),$". !"#$%!#&'&($"!))$* +($*,#&($"!)&*

%+,. 3.24. Сеть Петри для примера 2

%!#*%!#&F*:,$* $I*:+*

F*)&* !)!@&'! +($*,#)KH (*L*)&M

5@!"! 3

дов из какой-либо вершины, т.е. по наличию листьев — терминальных вершин. Неограниченный рост

числа маркеров в как ой-либо позиции свидетельствует о нарушениях ограниченности.

Приведем примеры анализа достижимости.

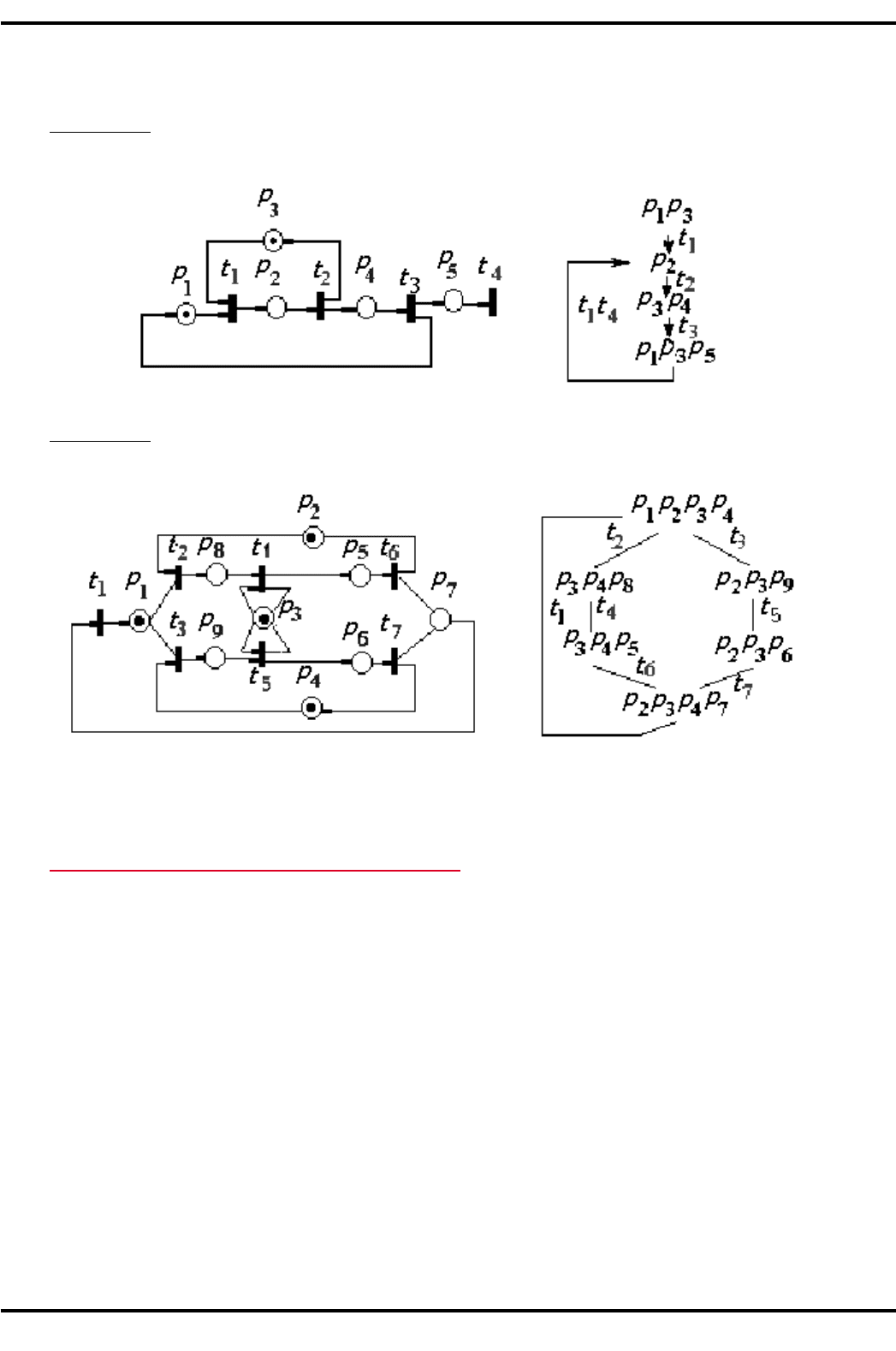
+-0B.- 7. Сеть Петри и граф достижимых разметок представлены на рис. 3.25.

На рисунке вершины графа изображены в виде маркировок, дуги помечены срабатывающими переходами. Живость

сети очевидна, так как срабатывают все переходы, тупики отсутствуют.

+-0B.- 2.

Сеть Петри и граф достижимых разметок представлены на рис. 3.26.

Сеть, моделирующая двухпроцессорную вычислительную систему с общей памятью, является живой, все размет-

ки достижимы.

3.7. E:-./:-+A.,74. 4B.,3.A.0+. 345,+,-./ /:I+0042 @8:H+7+ +

@.4/.-8+A. ,74@4 /45.D+849:0+>

'4/340.0-1 /:-./:-+A.,74@4 4B.,3.A.0+>. Подсистемы машинной графики и геометричес-

кого моделирования (МГиГМ) занимают центральное место в машиностроительных САПР-К. Конст-

руирование изделий в них, как правило, проводится в интерактивном режиме при оперировании гео-

метрическими моделями, т.е. математическими объектами, отображающими форму деталей, состав

сборочных узлов и возможно некоторые дополнительные параметры (масса, момент инерции, цвета

поверхности и т.п.).

В подсистемах МГиГМ типичный маршрут обработки данных включает в себя получение про-

ектного решения в прикладной программе, его представление в виде геометрической модели (геоме-

трическое моделирование), подготовку проектного решения к визуализации, собственно визуализа-

цию в аппаратуре рабочей станции и при необходимости корректировку решения в интерактивном ре-

жиме. Две последние операции реализуются на базе аппаратных средств машинной графики. Когда

говорят о математическом обеспечении МГиГМ, имеют в виду прежде всего модели, методы и алго-

ритмы для геометрического моделирования и подготовки к визуализации. При этом часто именно ма-

тематическое обеспечение подготовки к визуа лизации называют математическим обеспечением ма-

шинной графики.

Различают математическое обеспечение двумерного (2D) и трехмерного (3D) моделирования.

Основные применения 2D графики — подготовка чертежной документации в машиностроительных

САПР, топологическое проектирование печатных плат и кристаллов БИС в САПР электронной про-

&.+.)$(*),$". !"#$%!#&'&($"!))$* +($*,#&($"!)&*

%+,. 3.25. Сеть Петри и ее граф достижимости для примера 1

%+,. 3.26. Сеть Петри и ее граф достижимости для примера 2