Ниворожкина Л.И. Основы статистики с элементами теории вероятностей для экономистов: Руководство для решения задач
Подождите немного. Документ загружается.


где Х̃ — средняя по совокупности выбранных единиц; X — средняя по генеральной совокупности.
ген
— среднее квадратическое отклонение в генеральной совокупности.
Запись показывает, что о величине расхождения между параметром и статистикой
можно судить лишь с определенной вероятностью, от которой зависит величина t.
Формула (7.2) устанавливает связь между пределом ошибки, гарантируемым с некоторой вероятностью
Р, величиной t и средней ошибкой выборки
Согласно центральной предельной теореме Ляпунова, выборочные распределения статистик (при
п ≥V≥ 30) будут иметь нормальное распределение независимо от того, какое распределение имеет
генеральная совокупность. Следовательно,
где Ф
0
(t) — функция Лапласа.
Значения вероятностей, соответствующие различным t, содержатся в специальных таблицах:
при п > 30 — в таблице значений Ф
0
(t), а при n < 30 в таблице распределения t-Стьюдента. Неизвестное
значение
ген
при расчете ошибки выборки заменяется
выб
.
В зависимости от способа отбора средняя ошибка выборки определяется по-разному (табл. 7.1).
Таблица 7.1
Формулы расчета ошибки выборки для собственно-случайного отбора
Здесь
2
— выборочная дисперсия значений признака; ω (1 - ω ) — выборочная дисперсия доли
значений признака; n — объем выборки; N — объем генеральной совокупности; n/N — доля
обследованной совокупности; (1- n/N) — поправка на конечность совокупности (в литературе (1 - n/N)
иногда называется «поправкой на бесповторность отбора»).
7.4. Определение численности (объема) выборки
Одной из важнейших проблем выборочного метода является определение необходимого объема
выборки (табл. 7.2). От объема выборки зависит размер средней ошибки () и экономичность
проводимого выборочного наблюдения, так как чем больше объем выборки, тем больше затраты на
изучение элементов выборки, но тем меньше при этом ошибка выборки. Из формулы предельной
ошибки = t и формул средних ошибок выборки определяются формулы необходимой численности
81

выборки для различных способов отбора.
Таблица 7.2
Формулы, расчета необходимой численности выборки для собственно-случайного отбора
7.5. Интервальное оценивание
Пусть ε = X - X . Если представляет собой предел, которым ограничена сверху абсолютная
величина || < , то | Х -X | < . Следовательно,
Мы получили интервальную оценку генеральной средней. Из теоремы Чебышева следует, что
Интервальной оценкой называют оценку, которая определяется 2 числами — концами
интервала, который с определенной вероятностью накрывает неизвестный параметр
генеральной совокупности. Интервал, содержащий оцениваемый параметр генеральной
совокупности, называют доверительным интервалом. Для его определения вычисляется предельная
ошибка выборки , позволяющая установить предельные границы, в которых с заданной вероятностью
(надежностью) должен находиться параметр генеральной совокупности.
Предельная ошибка выборки равна t-кратному числу средних ошибок выборки. Коэффициент t
позволяет установить, насколько надежно высказывание о том, что заданный интервал содержит
параметр генеральной совокупности. Если мы выберем коэффициент таким, что высказывание в 95%
случаев окажется правильным и только в 5% — неправильным, то мы говорим: со статистической
надежностью в 95% доверительный интервал выборочной статистики содержит параметр
генеральной совокупности. Статистической надежности в 95% соответствует доверительная
вероятность — 0,95. В 5% случаев утверждение «параметр принадлежит доверительному интервалу»
будет неверным, т. е. 5% задает уровень значимости (
) или 0,05 вероятность ошибки. Обычно в
статистике уровень значимости выбирают таким, чтобы он не превысил 5% (
< 0,05). Доверительная
вероятность и уровень значимости дополняют друг друга до 1 (или 100%) и определяют надежность
статистического высказывания.
С помощью доверительного интервала можно оценить не только генеральную среднюю, но и другие
неизвестные параметры генеральной совокупности.
Для оценки математического ожидания а (генеральной средней)* нормально распределенного
количественного признака Х по выборочной средней X при известном среднем квадратическом
отклонении генеральной совокупности (на практике — при большом объеме выборки, т. е. при п ≥ 30)
и собственно-случайном повторном отборе формула (7.5) примет вид
где t определяется по таблицам функции Лапласа (приложение 2) из соотношения 2Ф
0
(t) = γ; — сред-
нее квадратическое отклонение; п — объем выборки (число обследованных единиц).
82

* Для нормально распределенной случайной величины М(X) = а X. Поэтому справедливо Р(X- а| < ) X.
Для оценки математического ожидания а (генеральной средней) нормально распределенного
количественного признака Х по выборочной средней X при известном среднем квадратическом
отклонении генеральной совокупности (при большом объеме выборки, т. е. при п ≥ 30) и собственно-
случайном бесповторном отборе формула (7.6) примет вид
Для оценки математического ожидания а (генеральной средней) нормально распределенного
количественного признака Х по выборочной средней Х при неизвестном среднем квадратическом
отклонении (σ генеральной совокупности (на практике — при малом объеме выборки, т. е. при п < 30) и
собственно-случайном повторном отборе формула (7.6) будет иметь вид
где t определяется по таблицам Стьюдента (приложение 5), по уровню значимости α = 1 — и числу
степеней свободы k = п — 1; — исправленное выборочное среднее квадратическое отклонение; п —
объем выборки.
Для оценки математического ожидания а (генеральной средней) нормально распределенного
количественного признака Х по выборочной средней X при неизвестном среднем квадратическом
отклонении σ- генеральной совокупности (при малом объеме выборки, т. е. при п < 30) и собственно-
случайном бесповторном отборе формула (7.8) примет вид
Для оценки генеральной доли р нормально распределенного количественного признака по
выборочной доле ω= т/п (при большом объеме выборки, т. е. при п 30) и собственно-случайном
повторном отборе формула (7.5) будет иметь вид
83

где t определяется по таблицам функции Лапласа (приложение 2) из соотношения 2Ф
0
(t) = ; ω —
выборочная доля; п — объем выборки (число обследованных единиц);
Для оценки генеральной доли р нормально распределенного количественного признака по выбо-
рочной доле ω = т/п (при большом объеме выборки, т. е. при п 30) и собственно-случайном
бесповторном отборе формула (7.10) примет вид
Для оценки генеральной доли р нормально распределенного количественного признака по
выборочной доле ω = т/п (при малом объеме выборки, т. е. при п < 30) и собственно-случайном
повторном отборе формула (7.10) примет вид
где t определяется по таблицам Стьюдента (приложение 5), по уровню значимости α = 1 - γ и числу
степеней свободы k = п - 1.
Для оценки генеральной доли р нормально распределенного количественного признака по
выборочной доле ω = т/п (при малом объеме выборки, т. е. при п < 30) и собственно-случайном
беспоторном отборе формула (7.12) будет иметь вид
84

Пример 1. С помощью собственно-случайного повторного отбора руководство фирмы провело
выборочное обследование 900 своих служащих. Средний стаж их работы в фирме равен 8,70 года, а
среднее квадратическое (стандартное) отклонение — 2,70 года. Среди обследованных оказалось 270
женщин. Считая стаж работы служащих фирмы распределенным по нормальному закону, определите:
а) с вероятностью 0,95 доверительный интервал, в котором окажется средний стаж работы всех
служащих фирмы; б) с вероятностью 0,90 доверительный интервал, накрывающий неизвестную долю
женщин во всем коллективе фирмы.
Решение. По условию задачи выборочное обследование проведено с помощью собственно-
случайного повторного отбора. Объем выборки п = 900 единиц, т. е. выборка большая.
а) Найдем границы доверительного интервала среднего стажа работы всего коллектива фирмы, т. е.
границы доверительного интервала для генеральной средней.
По условию X = 8,70; = 2,70; п = 900; = 0,95. Используем формулу
Найдем t из соотношения 2Ф
0
(t) = : 2Ф
0
(t) = 0,95; Ф
0
(t) = 0,95/2 = 0.475.
По таблице функции Лапласа (приложение 2) найдем, при каком t Ф
0
(t) = 0,475. Ф
0
(1,96) = 0,475.
Следовательно, t = 1,96.
Найдем предельную ошибку выборки
С вероятностью 0,95 можно ожидать, что средний стаж работы всего коллектива фирмы находится в
интервале от 8,5236 до 8,8764 года.
б) Теперь оценим истинное значение доли женщин во всем коллективе фирмы.
По условию т = 270; п = 900; γ= 0,90.
Выборочная доля ω = 270/900 = 0,30.
85

Используем формулу
Найдем t из соотношения 2Ф
0
(t) = γ 2Ф
0
(t) = 0,90; Ф
0
(t) = 0,90/2 = 0,45.
По таблице функции Лапласа (приложение 2) определим, при каком t Ф
0
(t) = 0,45. Ф
0
(1,64) = 0,45.
Следовательно, t = 1,64.
Предельная ошибка выборки определяется по формуле
Итак, с вероятностью 0,90 можно ожидать, что доля женщин во всем коллективе фирмы находится в
интервале от 0,2749 до 0,3251.
Ответ. Можно ожидать, что с вероятностью 0,95 средний стаж работы всех служащих фирмы
находится в интервале от 8,5236 до 8,8764 года. С вероятностью 0,90 можно гарантировать, что доля
женщин во всем коллективе фирмы находится в интервале от 0,2749 до 0,3251.
Пример 2. Изменим условие примера 1.
1) С помощью собственно-случайного повторного отбора определяется средний стаж работы служащих
фирмы. Предполагается, что он подчиняется нормальному закону. Каким должен быть объем выборки,
чтобы с доверительной вероятностью 0,95 можно было утверждать, что, принимая полученный средний
стаж работы за истинный, совершается погрешность, не превышающая 0,50 года, если стандартное
отклонение σ равно 2,70 года?
2) Каким должен быть объем собственно-случайной повторной выборки, чтобы с надежностью 0,90
можно было утверждать, что максимальное отклонение выборочной доли женщин в выборке от доли
женщин во всем коллективе фирмы не превышало 0,05, если в прошлом аналогичном обследовании
выборочная доля женщин оказалась равной 0,30?
Решение. В данной задаче нужно найти необходимую численность выборки. Ее расчет дает ответ на
вопрос: «Сколько нужно обследовать единиц совокупности, чтобы с заранее заданной вероятностью не
превысить заранее заданную ошибку?»
1) Дано: = 0,50; = 2,70;= 0,95.
По условию задачи требуется найти необходимую численность выборки для средней при повторном
отборе. Воспользуемся формулой расчета необходимой численности выборки для средней при
собственно-случайном повторном отборе: п = t
2
2
/
2
.
Неизвестное значение t найдем из соотношения 2Ф
0
(t) = 2Ф
0
(t) = 0,95; Ф
0
(t)= 0,95/2 = 0,475.
86
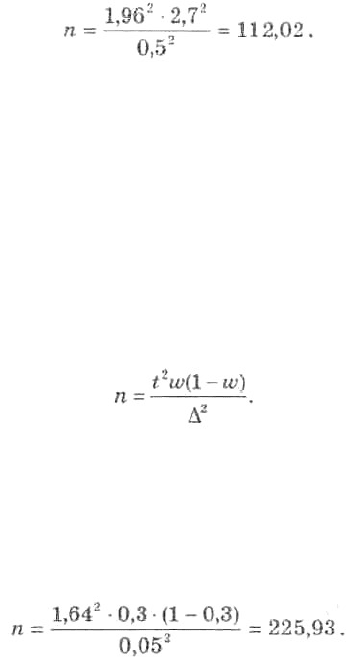
По таблице функции Лапласа (приложение 2) найдем, при каком t Ф
0
(t) = 0,475. Ф
0
(1,96) = 0,475.
Следовательно, t = 1,96.
Рассчитаем необходимую численность выборки
Так как п — целое число, округлим полученный результат до большего целого, учитывая, что
необходимо не превышать заданную ошибку.
Следовательно, надо обследовать не менее 113 служащих.
Ответ. Чтобы с вероятностью 0,95 и D = 0,50 года с помощью собственно-случайного повторного
отбора определить средний стаж работы в фирме, необходимо обследовать не менее 113 служащих.
2) Дано: = 0,05; ω = 0,30; = 0,90.
По условию задачи требуется найти необходимую численность выборки для доли при собственно-
случайном повторном отборе.
Воспользуемся формулой расчета необходимой численности выборки для доли при собственно-
случайном повторном отборе:
Найдем t из соотношения 2Ф
0
(t) = . 2Ф
0
(t) = 0,90; Ф
0
(t) = 0,90/2 = 0,45.
По таблице функции Лапласа (приложение 2) найдем, при каком t Ф
0
(t) = 0,45. Ф
0
(1,64) = 0,45.
Следовательно, t = 1,64.
Рассчитаем необходимую численность выборки:
Так как п — целое число, округлим полученный результат до большего целого, учитывая, что
необходимо не превышать заданную ошибку.
Следовательно, п ≈ 226.
Ответ. Чтобы с вероятностью 0,90 и ошибкой 0,05 с помощью собственно-случайного повторного
отбора определить долю женщин во всем коллективе фирмы, необходимо обследовать не менее 226
служащих.
Пример 3. Владелец автостоянки опасается обмана со стороны своих служащих (охраны
автостоянки). В течение года (365 дней) владельцем автостоянки проведено 40 проверок. По данным
проверок среднее число автомобилей, оставляемых на ночь на охрану, составило 400 единиц, а среднее
квадратическое (стандартное) отклонение их числа — 10 автомобилей. Считая отбор собственно-
случайным, с вероятностью 0,99 оцените с помощью доверительного интервала истинное среднее число
автомобилей, оставляемых на ночь на охрану. Обоснованы ли опасения владельца автостоянки, если по
отчетности охранников среднее число автомобилей, оставляемых на ночь на охрану, составляет 395
автомобилей?
Решение. По условию задачи выборочное обследование проведено с помощью собственно-
случайного отбора. Очевидно, что отбор — бесповторный, так как не имеет смысла производить
проверку более 1 раза в сутки. Объем выборки n = 40, что больше 30 единиц, т. е. выборка большая.
Объем генеральной совокупности N = 365.
Найдем границы доверительного интервала для оценки среднего числа автомобилей, оставляемых на
ночь на охрану, т.е. границы доверительного интервала для генеральной средней.
По условию
Х= 400; = 10; п = 40; = 0,99; N=365. Используем формулу
87

Найдем t из соотношения 2Ф (t) = . 2Ф
0
(t) = 0,99; Ф
0
(t) = 0,99/2 = 0,495.
По таблице функции Лапласа (приложение 2) найдем, при каком t Ф
0
(t) = 0,495. Ф
0
(2,58) = 0,495.
Следовательно, t = 2,58.
Найдем предельную ошибку выборки:
Ответ. С уверенностью в 99% можно ожидать, что среднее число автомобилей, оставляемых на ночь
на охрану, находится в интервале от 396 до 404. Таким образом, можно утверждать, что служащие
автостоянки обманывают ее владельца.
Пример 4. В 24 из 40 проверок число автомобилей на автостоянке не превышало 400 единиц. С
вероятностью 0,98 найдите доверительный интервал для оценки истинной доли дней в течение года,
когда число оставляемых на стоянке автомобилей не превышало 400 единиц.
Решение. Определим границы доверительного интервала для доли дней в течение года, когда число
оставляемых на стоянке автомобилей не превышало 400 единиц.
По условию т = 24; п = 40; =.0,98.
Выборочная доля ω = 24/40 = 0,60. Так как
то найдем t из соотношения 2Ф
0
(t) = . 2Ф
0
(t) = 0,98; Ф
0
(t) = 0,98/2 = 0,49.
По таблице функции Лапласа (приложение 2) найдем, при каком t Ф
0
(t) = 0,49. Ф
0
(2,33) = 0,49.
Следовательно, t = 2,33.
Найдем предельную ошибку выборки:
88

Ответ. С вероятностью 0,98 можно ожидать, что доля дней в течение года, когда число оставляемых
на стоянке автомобилей не превышало 400 единиц, находится в интервале от 0,4297 до 0,7703.
Пример 5. Изменим условие примера 3.
С помощью собственно-случайного бесповторного отбора определяется среднее число автомобилей,
оставляемых на ночь на охрану. Предполагается, что оно подчиняется нормальному закону. Каким
должен быть объем выборки, чтобы с вероятностью 0,95 можно было утверждать, что когда
принимается полученное среднее число автомобилей по выборке за истинное, совершается
погрешность, не превышающая 3 автомобилей, если среднее квадратическое отклонение равно 10
автомобилям?
Решение. Дано: = 3; σ = 10; = 0,95; N=365. Воспользуемся формулой расчета необходимой
численности выборки для средней при собственно-случайном бесповторном отборе;
Найдем t из соотношения 2Ф
0
(t) = . 2Ф
0
(t) = 0,95; Ф
0
(t) = 0,95/2 = 0,475.
По таблице функции Лапласа (приложение 2) найдем, при каком t Ф
0
(t) = 0,475. Ф
0
(1,96) = 0,475.
Следовательно, t = 1,96.
Рассчитаем объем выборки:
Так как п — целое число, округлим полученный результат до большего целого, учитывая, что
необходимо не превышать заданную ошибку.
Следовательно, необходимо провести не менее 39 проверок.
Ответ. Для определения среднего числа автомобилей, оставляемых на ночь на охрану с
вероятностью 0,95 и = 3, необходимо провести не менее 39 проверок.
Пример 6. Изменим условие примера 4.
Каким должен быть объем собственно-случайной бесповторной выборки, чтобы с вероятностью 0,90
можно было утверждать, что максимальное отклонение выборочной доли дней от доли дней в течение
года (когда среднее число оставляемых на охрану автомобилей не превышало 400 единиц) не
превышало 0,10, если по данным прошлых проверок выборочная доля таких дней составляла 0,60?
89

Решение. Дано: Δ = 0,10; ω = 0,60; = 0,90; N=365. Воспользуемся формулой расчета необходимой
численности выборки для доли при собственно-случайном бесповторном отборе
Найдем t из соотношения 2Ф
0
(t) = у. 2Ф
0
(t) = 0,90; Ф
0
(t) = 0,90/2 = 0,45.
По таблице функции Лапласа (приложение 2) найдем, при каком t Ф
0
(t) = 0,45. Ф
0
(1,64) = 0,45.
Следовательно, t = 1,64.
Рассчитаем необходимую численность выборки:
Так как п — целое число, округлим полученный результат до большего целого, учитывая, что
необходимо не превышать заданную ошибку.
Следовательно, n 55.
Ответ. Для того чтобы с вероятностью 0,90 и предельной ошибкой 0,10 с помощью собственно-
случайного бесповторного отбора определить искомую долю дней в течение года, необходимо провести
не менее 55 проверок.
Пример 7. Служба контроля энергосбыта провела выборочную проверку расхода электроэнергии
жителями одного из многоквартирных домов. С помощью собственно-случайного отбора выбрано 10
квартир и определен расход электроэнергии в течение одного из летних месяцев (кВт · ч): 125; 78; 102;
140; 90; 45; 50;125; 115;112.
С вероятностью 0,95 определите доверительный интервал для оценки среднего расхода
электроэнергии на 1 квартиру во всем доме при условии, что в доме 70 квартир, а отбор был: а)
повторным; б) бесповторным.
Решение. По условию задачи выборочное обследование проведено с помощью собственно-
случайного отбора. Объем выборки n = 10 единиц, т. е. выборка малая.
а) Считая отбор повторным, найдем доверительный интервал для оценки среднего расхода
электроэнергии на 1 квартиру во всем доме, т. е. границы доверительного интервала для оценки
генеральной средней.
Для этого используем формулы:
Для определения границ доверительного интервала необходимо рассчитать выборочные среднюю и
среднее квадратическое (стандартное) отклонение.
Рассчитаем выборочную среднюю арифметическую:
Найдем исправленную выборочную дисперсию:
90
