Никульчев Е.В. Практикум по теории управления в среде Matlab

Подождите немного. Документ загружается.

Практическое занятие № 4.

УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ

Цель работы

Ознакомление с критериями устойчивости и выявление у

заданной управляемой линейной системы с полной обратной связью

свойства асимптотической устойчивости.

Постановка задачи

Задана система управления, описываемая конечно-разностными

уравнениями в пространстве состояний

x(k+1) = A(k) x(k) + B(k) u(k), (

Nk ,0= ), (4.1)

и известна матрица K, определяющая закон управления u = Kx.

Требуется определить асимптотическую устойчивость систему с

полной обратной связью.

Краткие сведения из теории

Система управления называется устойчивой по Ляпунову, если

при ненулевых ограниченных начальных условиях свободное движение

ограничено.

Согласно определению, система (4.1) асимптотически устойчива,

если для любого начального состояния x(0) = x

, ее решение х(k, x

)

стремится к нулю по норме, при k→∞.

Существует большое количество критериев, являющихся

достаточным условием устойчивости. Для линейных систем

устойчивость системы являются асимптотически устойчивыми.

Для того, что бы система (4.1) была асимптотически устойчива,

необходимо, что все собственные числа матрицы А + ВL по модулю

меньше единицы. По определению, собственными числами λ матрицы

А + ВL являются корни характеристического уравнения

det (λE − [А + ВL]). Здесь E – единичная матрица.

–

51 –

Мощным инструментом исследования устойчивости

динамических систем является метод функций Ляпунова. Для линейных

автономных систем существование функции Ляпунова в виде

квадратичной формы является одновременно необходимым и

достаточным условием равномерной асимптотической устойчивости в

целом.

Рассмотрим линейную стационарную систему



(4.2)

Допустим, что нам удалось найти функцию Ляпунова: V(x)=x

Qx, где

Q – симметричная и положительная определенная матрица. Тогда

(

)



()



x x Qx x Qx x A Qx x QAx x A Q QA x

TT TTT TT

=+= + = + (4.3)

Обозначим

AQ QA

= – С, (4.4)

тогда, поскольку С положительно определенна, то система

асимптотически устойчива в целом. Более того, т.к.

()

(

)

(

)

CAQQA QAAQ QAAQ

TTT T

=− + =− + =− + =−C,

то матрица С симметрична.

На практике целесообразно решать обратную задачу. Выбирают

какую-либо положительно определенную положительную матрицу,

например C = I. Тогда из (4.4) можно получить Q. Если квадратичная

форма Q оказывается неопределенной (знакопеременной), то по теореме

Ляпунова о неустойчивости начало координат неустойчиво. Если Q

положительно определена, то поскольку система линейна и

стационарна, начало координат асимптотически устойчиво в целом.

Обоснованность такого анализа зависит от того, определяет ли

уравнение (4.4) однозначно матрицу Q, если задана симметричная и

положительная С.

Справедливы следующие утверждения:

Если n собственных значений λ

, …, λ

матрицы A таковы, что

+λ

≠ 0 (

ij n,,=1

), то из уравнения (4.4) при заданной матрице С

матрица Q определяется однозначно. (Достаточное условие

устойчивости матрицы А).

–

52 –

Если матрица А устойчива и матрица С положительно определена, то

матрица Q также положительно определена. (Необходимое условие

устойчивости матрицы А).

Система (4.1) асимптотически устойчива в том и только том

случае, если решение Г, являющееся (n×n)-матрицей, уравнения

Ляпунова

HBLABLA

−=Γ−+Γ+ )()(

, (4.5)

является положительно-определенной матрицей. Здесь H –

произвольная положительно-определенная симметричная матрица. Для

определенности в уравнении (4.5) матрицу H можно положить

единичной.

Для установления положительной определенности симметричной

матрицы Г можно воспользоваться критерием Сильвестра: ∆

> 0 для

ni ,1= , где ∆

– миноры i-го порядка матрицы Г.

Для определения асимптотической устойчивости линейных

систем можно воспользоваться критерием Раусса-Гурвица. Согласно

этому критерию, система (4.2) является устойчивой, если все миноры

матрицы Гурвица были положительны. Матрица Гурвица имеет вид

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−−−

531

000

aaa

nnn

"""""

Здесь a

– коэффициенты характеристического полинома матрицы A:

det (λE – A) = .

... aaa

++λ+λ

−

Асимптотическая устойчивость определяется аналогично, только

вместо матрицы A берется матрица A+BL.

Последовательность выполнения работы

Для определения асимптотической устойчивости линейных

стационарных систем в Control System Toolbox имеются команды,

приведенные в таблице 4.1.

–

53 –

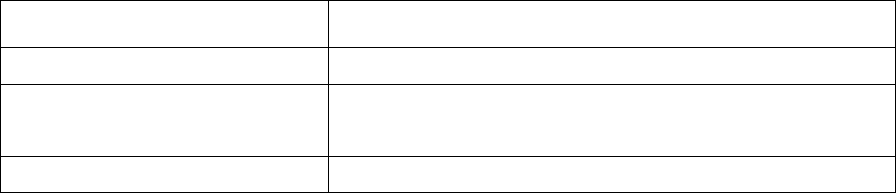
Таблица 4.1. Команды

Control System Toolbox

Синтаксис Описание

Q = lyap(A, C)

Решение непрерывных уравнений Ляпунова

Q = lyap(A, X, Y)

Решение непрерывных обобщенных

уравнений Ляпунова (уравнений Сильвестра)

Г = dlyap(A, H)

Решение дискретных уравнений Ляпунова

Функция

Q = lyap(A, С)

находит решение системы уравнений Ляпунова вида (4.4).

Функция

Q = lyap(A, X, Y)

находит решение уравнений Сильвестра (обобщенных уравнений

Ляпунова) вида:

−

Функции решения непрерывных уравнений Ляпунова выдают

результат только в случае единственности решения, т.е. в случае, когда

собственные значения

матрицы A и собственные значения

матрицы X для всех (i, j) удовлетворяют условию

,...,,

1 n

λλ

,...,,

λλ

≠λ+λ

Функция

Г = dlyap(A, H)

находит решение системы уравнений Ляпунова вида (4.5). Результат

решения уравнений Ляпунова для дискретных систем выдается только в

случае единственности решения, т.е., когда собственные значения

матрицы A для всех (i, j) удовлетворяют условию

,...,,

1 n

λλ

≠

–

54 –

Таким образом, выполнение лабораторной работы состоит из

следующих шагов:

Изучить теоретические сведения.

Запустить систему MATLAB.

Создать ss-объекта, в соответствии с заданным вариантом.

Определить устойчивость системы.

Определить устойчивость системы с полной обратной связью.

Построить графики динамики системы при ненулевых

начальных условиях.

Оформить отчет.

Сдать отчет преподавателю и защитить лабораторную работу.

Методический пример

Задана система управления, описываемая конечно-разностными

уравнениями в пространстве состояний

x(k+1) = A(k) x(k) + B(k) u(k), (

Nk ,0= ),

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−

и известна матрица K, определяющая закон управления u = Kx,

⎟

⎠

⎞

⎜

⎝

⎛

1. Зададим матрицы, определяющие систему:

>> A=[1 2; -3 4]

A =

1 2

-3 4

>> B= [1 2]'

B =

>> L=[2 1]

L =

2 1

–

55 –

2. Определим решение уравнения Ляпунова

>> G=dlyap(A, eye(2))

G =

-0.2211 -0.1215

-0.1215 -0.1285

3. Произведем расчет главных миноров

>> det(G(1:1, 1:1))

ans =

-0.2211

>> det(G)

ans =

0.0136

По критерию Сильвестра решение не является положительно-

определенной матрицей, следовательно, система не является

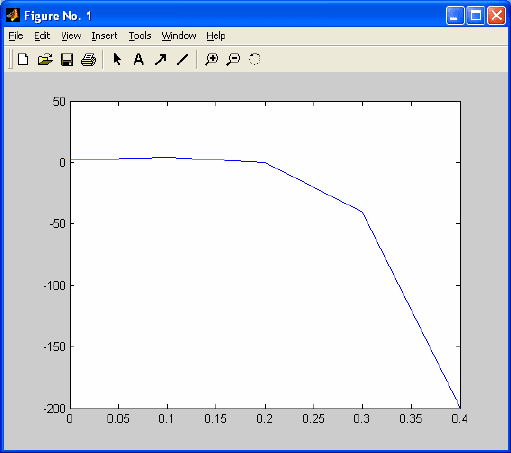
асимптотически устойчивой. График свободного движения системы при

начальных условиях

)1,2(),(

= xxx

показан на рис. 4.1 и 4.2.

Рис. 4.1. x

(k).

–

56 –

Рис. 4.2. x

(k).

4. Аналогично можно определить свойство асимптотической

устойчивости в управляемой системе.

>> G=dlyap(A+B*L, eye(2))

G =

-0.2563 0.0833

0.0833 -0.0498

>> det(G)

ans =

0.0058

>> det(G(1:1, 1:1))

ans =

-0.2563

По критерию Сильвестра решение дискретного уравнения

Ляпунова не является положительно-определенной матрицей,

следовательно, система не является асимптотически устойчивой.

5. Приведем текст script-файла для определения устойчивости

матрицы X на основе использования метода Раусса-Гурвица.

–

57 –

%получение коэффициентов характеристического полинома

lm= poly(X);

%определение размерности

[L, N] =size(lm);

%создание матрицы с нулевыми значениями

g=zeros(N, N);

%заполнение нечетных строк матрицы Гурвица

s=0;

for i=1:2:N

j=1;

j=j+s;

r=0;

for r=2:2:N

g(i, j)=lm(r);

j=j+1;

end

s=s+1;

end

%заполнение четных строк матрицы Гурвица

s=0;

for i=2:2:N

j=1;

j=j+s;

r=0;

for r=1:2:N

g(i, j)=lm(r);

j=j+1;

end

s=s+1;

end

g=g(1:N-1, 1:N-1);

%вычисление главных миноров

minor=1;

for i=1:N-1

dd = det(g(1:i, 1:i));

if dd<0

minor=0;

end

%вывод результатов

if minor==0

disp('СИСТЕМА НЕ УСТОЙЧИВА');

else

disp('СИСТЕМА УСТОЙЧИВА');

end

–

58 –

Результат вычисления показывает, что система управления не

является асимптотически устойчивой.

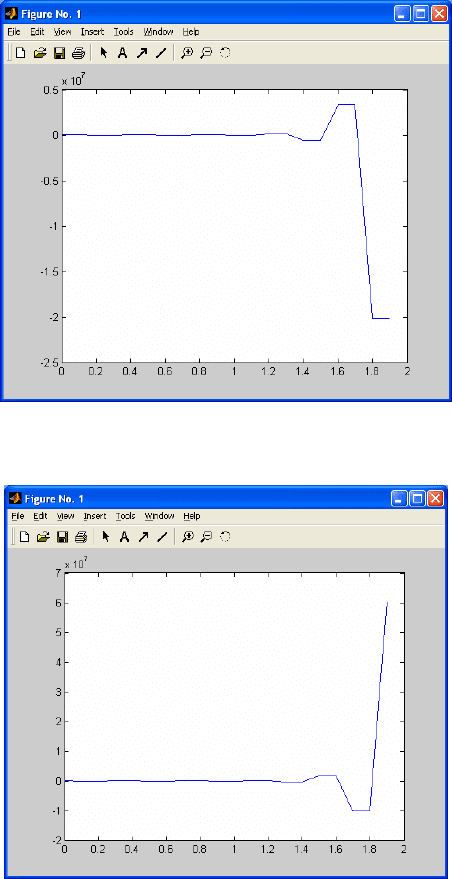
График динамики управляемой системы при начальных условиях

показан на рис. 4.3 и 4.4.

)1,2(),(

== xxx

Рис. 4.3. x

(k).

Рис. 4.4.. x

(k).

Полученные графики динамики системы иллюстрируют

полученный аналитический результат о неустойчивости системы.

–

59 –

Отчет о работе

Отчет оформляется в соответствии с требованиями,

предъявляемыми к оформлению лабораторных работ в вузе, и должен

содержать:

Титульный лист

Наименование и цель работы.

Порядок и результаты определения асимптотической

устойчивости заданной системы и системы с управлением с

полной обратной связью методами функций Ляпунова и

Раусса-Гурвица.

Анализ результатов и выводы.

Контрольные вопросы

Дать определение устойчивости Ляпунова и асимптотической

устойчивости.

Покажите, что для линейных систем всегда можно найти

функцию Ляпунова.

Постройте матрицу Гурвица и примените критерий Раусса-

Гурвица для определения устойчивости типовых звеньев САУ.

Выясните, существуют ли связь между переходной

характеристикой системы и свойством асимптотической

устойчивости.

Используя технику приведения матриц к канонической форме

Фробениуса, получите критерий Раусса-Шура.

–

60 –