Непейвода Н.Н., Скопин И.Н. Основания программирования

Подождите немного. Документ загружается.

9.3. СТРУКТУРНЫЕ ТИПЫ

525

Если тип индексов всегда один и тот же (обычно отрезок целых неотрица-

тельных, как в

С/С++

), то он может опускаться.

Массивы бывают статическими,динамическими и гибкими. Для статиче-

ских массивов границы изменения индексов задаются статически вычисли-

мыми выражениями (состоящими из констант и переменных периода ком-

пиляции), для динамических массивов — выражениями, значения которых

должны быть вычислены до выполнения определения типа массивов. Про

гибкие массивы говорят, что они имеют подвижные границы, т. е. такие, ко-

торые могут изменяться в процессе оперирования с массивом.

Подвижные границы чаще всего указываются специальным служебным

словом.Если значение нижних границ всех массивов стандартизовано (в

С/С++

это 0), оно опускается. В

С/С++

задание верхней границы индекса массива —

это указание границ безопасного обращения к элементам массива. В строгом

смысле этого слова она границей не является, поскольку никакой ошибки не

будет, если индексное выражение выйдет за указанный предел. Последнее в

точности соответствует трактовке массивов как указателей на область памя-

ти.

Массив есть таблично задаваемая функция, переводящая область ин-

дексов в область компонент. Если D — область изменения индексов (одно-

мерная для векторов или многомерная в других случаях), а R — множество

(область) значений компонент, то

M : D → R.

Точнее, это семейство функций, если иметь в виду возможность присваивать

компоненте новое значение. Хоар эту операцию называет выборочным обно-

влением массива.

Как правило, в качестве имени этой функции (семейства функций) выби-

рают имя переменной типа массив.

Чтобы полностью специфицировать значение типа массив, нужно ука-

зать для каждого элемента D значение из R. Этот выбор делается независимо

для каждого элемента массива. В результате

мощность

(D → R) =

мощность

(R)

мощность

(D)

Таким образом, при представлении моделируемых объектов массивами за-

даются все значения для всех индексов, тогда как это может противоречить

реальности (массив дней месяца).

526

ГЛАВА 9. СТРУКТУРЫ ДАННЫХ

Не следует путать последнее с так называемыми разреженными масси-

вами, у которых для большинства элементов принимается стандартное зна-

чение (как правило, 0; пример — диагональная матрица), либо большинство

элементов не используется (случаи, подобные дням месяца, — это издерж-

ки неадекватности абстрактной структуры конкретному содержанию). С аб-

страктной точки зрения разреженный массив ничем не отличается от обыч-

ного (чаще гибкого) массива. Поэтому было бы правильно (как в языке

Java

)

не делать различий между ними при изображении массивов в программе.

Различия появляются, когда выбираются представления массивов. Так, для

диагональной матрицы (D) естественным представлением является вектор

(

rep

) со следующим доступом (i, j — индексные выражения):

D[i,j] = (i == j? Drep[i]: exception);

Здесь

exception

— указание того, что с разными индексами

D[i,j]

употреблять-

ся не должна. Возможно, что это присваивание в некоторых программах ра-

зумно трактовать как порождение новой матрицы (с тем же именем), но уже

недиагональной.

Другой пример — симметричная матрица, которую, чтобы вдвое сокра-

тить расход памяти, стоит представлять вектором,содержащим все элементы

без дублирования (

— выражение типа компоненты массива):

D[i, j] :

read

(i, j) = (S

(D, i, j)) =

if i > j then(S

(D, j, i))

else(S

(

rep

, ϕ(i, j));

write

(i, j, x) = (S

(D, i, j) := x) =

if i > j then(S

(D, j, i) := x)

else(S

(

rep

, ϕ(i, j)) := x)

(9.4)

Здесь ϕ(i, j) —некоторая функция (зависящая от порядка,в котором предста-

влены элементы матрице в векторе), которая вычисляет расположение (i,j)-

того элемента матрицы (D) в векторе

rep

В плане реализации доступа, смешивающего многомерные и линейные

представления массивов, преуспел Фортран с его

COMMON

-блоками и опе-

ратором

EQUIVALENCE

Наиболее распространенное представление массивов — такое, когда ка-

ждому элементу отводится одно или несколько машинных слов. Каждый эле-

мент адресуется непосредственно. Это представление называется стандарт-

ным.

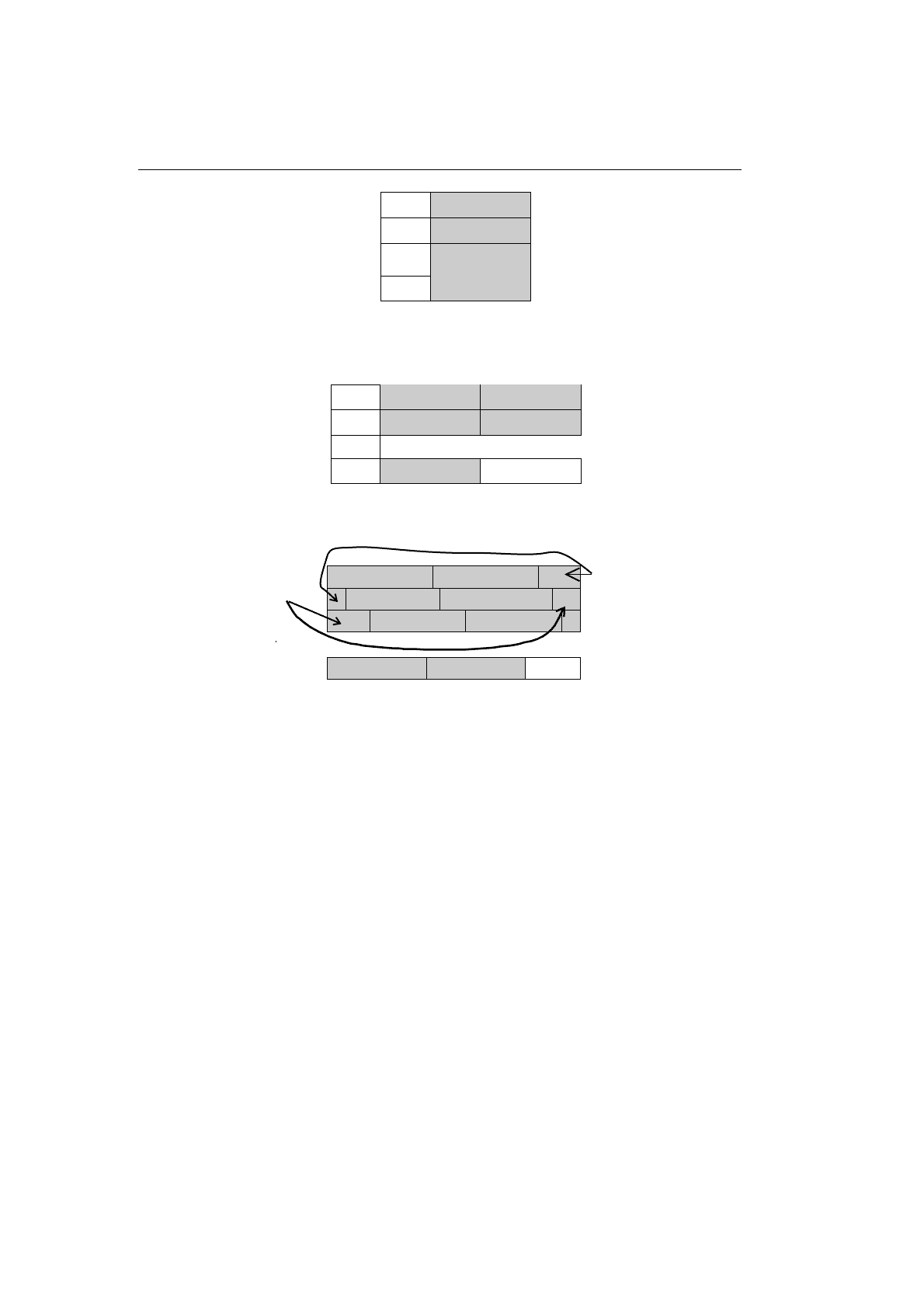
9.3. СТРУКТУРНЫЕ ТИПЫ

527

a[0]

a[1]

...

a[n]

Здесь и далее закраской выделена заполненная часть машинного слова; то,

что осталось без закраски, — неинформативная часть (т. е. потери памяти).

Следующее представление называется представлением со свободной упа-

ковкой:

a[0] a[1]

a[2] a[3]

...

a[n]

Когда нужно экономить память, применяют представления с жесткой упа-

ковкой (см. рис. 9.5). Когда разрабатывается представление для массивов,

A: A[0] A[1] A[2]

A[3] A[4]

A[5]

A[6] A[7]

...

A[n]

Рис. 9.5. Упакованное представление массива

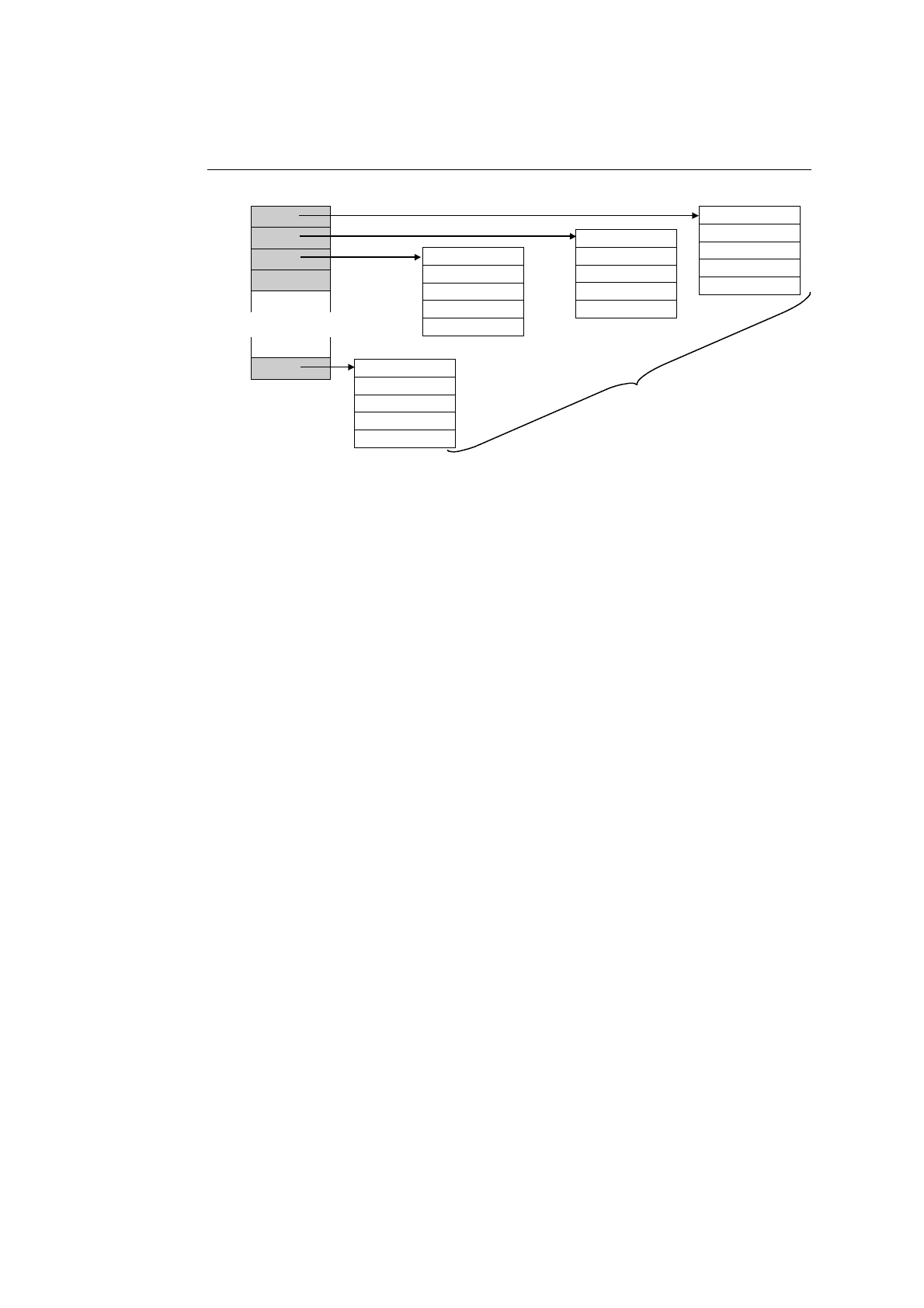
компоненты которых сами являются массивами, асто используется ссылоч-

ное представление (см. рис. 9.6).

В случаях разреженных и ассоциативных массивов нужно гораздо боль-

шее искусство выбора представлений. В обоих случаях надо учитывать, что

со многими компонентами работа не производится. В случае разреженного

массива к тому же заранее известно, что далеко не все компоненты массива

фактически используются, а потому не нужно их хранить.

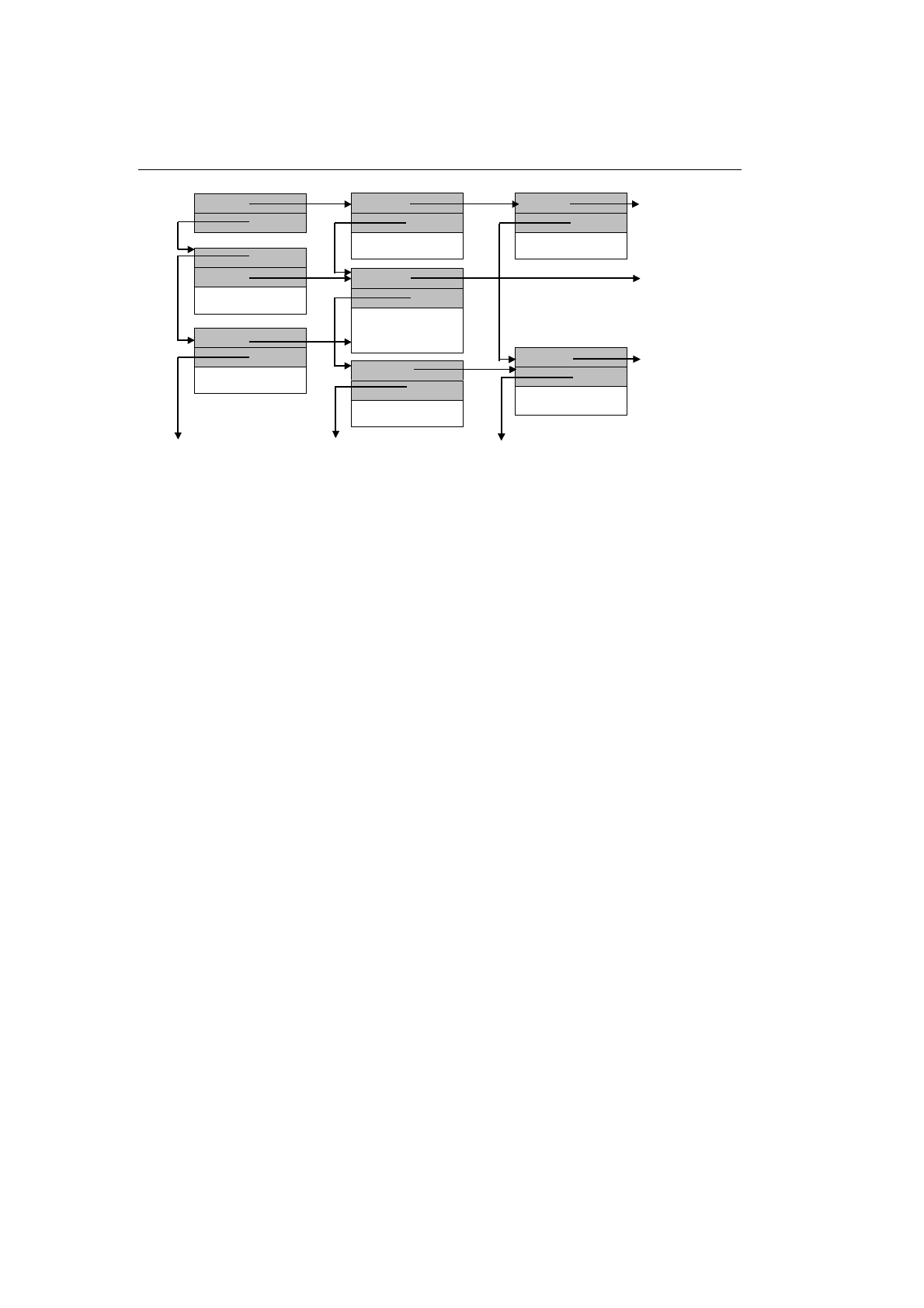
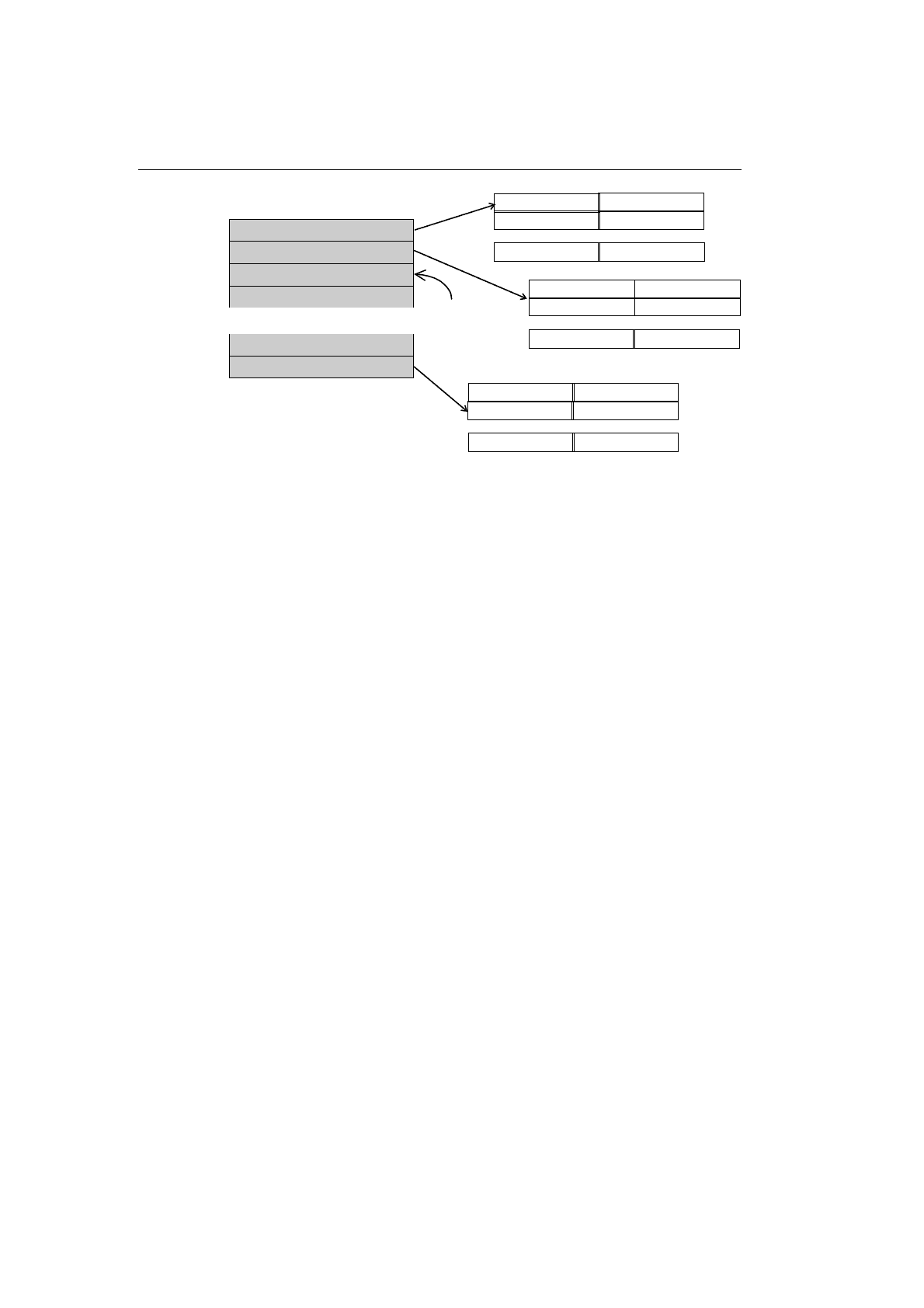
Примером такого представления может служить решетчатое представле-

ние (см. рис. 9.7).

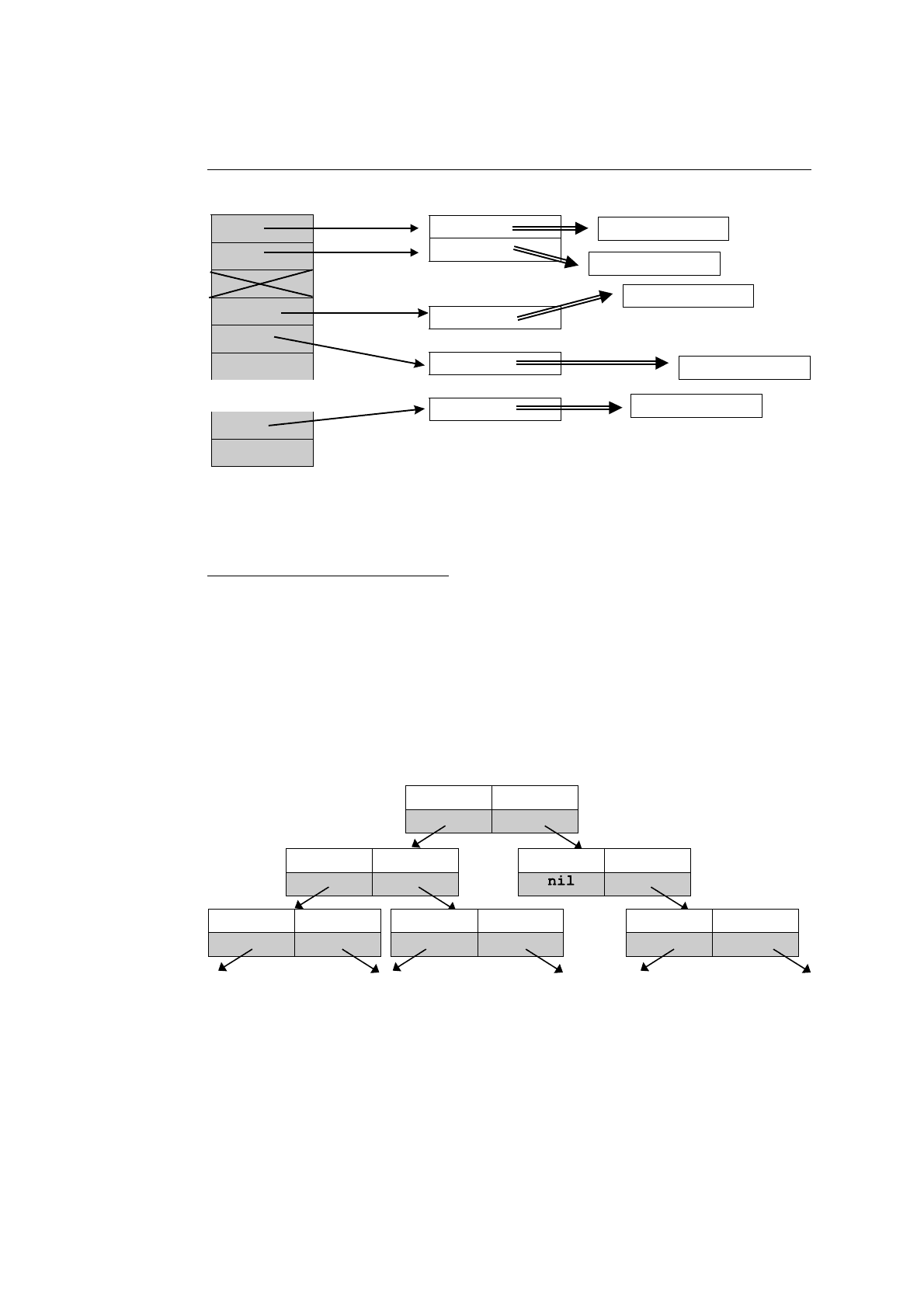
Примером представления,подходящего для ассоциативных массивов, явля-

ется ключевое представление, когда по индексу вычисляется ключ, а уже по

ключу размещается значение (см. рис. 9.8). Здесь двойная стрелка означает

528

ГЛАВА 9. СТРУКТУРЫ ДАННЫХ

Первое измерение:

…

Второе

измерение

Рис. 9.6. Ссылочное представление

один из вариантов представления записи

(

<ключ, если для него есть компонент>,

которая в ключевом представлении заменяет исходный компонент разрежен-

ного массива.

Таким образом, доступ к компоненте становится двухступенчатым:

1. выбор нужной компоненты в новом наборе (логически это снова мас-

сив, но уже плотный) и

2. извлечение K

из записи (второе поле).

Старый индекс для такого представления называется ключом, а порядковые

номера компонентов нового набора — индексами записей нового набора.

При ключевом доступе возникает задача контроля целостности: в но-

вом наборе не должны появляться записи с одинаковыми ключами, и нужно

контролировать,не нарушается ли упорядоченность ключей.Ключевое пред-

ставление можно рассматривать как следующий по отношению к исходному

массиву уровень абстракции (более нижний, реализационный), который, в

свою очередь, допускает различные реализации двухступенчатого доступа.

Указанная запись может представляться стандартным способом, со свобод-

ной упаковкой (реже) или с использованием ссылок (очень часто). С учетом

упорядоченности ключей (обычное свойство для ассоциативных массивов —

9.3. СТРУКТУРНЫЕ ТИПЫ

529

Нет значения

Граничная

цепочка d1

Остаток этого

столбца

…

Остаток этого

столбца

…

Остаток

этого ряда

…

Остаток

этого ряда

…

A[d1’,d2’]

A[d1,d2’]

A[d1,d2]

d1’

A[d1’,d2]

d2’

Рис. 9.7. Решетчатое представление массива

см. выше)целесообразно предложить организацию индексов, приспособлен-

ную для дихотомического поиска. Здесь возможны варианты:

1. Индексы представляются как последовательность регистров со ссыл-

ками на Ключи,которая соответствует упорядоченности ключей —пря-

молинейная реализация.

2. По значениям ключей вместо массива

Индексы

строится B-дерево,обес-

печивающее хорошую стратегию оперирования.

Значение ключа вершины, к которой ведет левая дуга, всегда больше

значения ключа родительской вершины, которое, в свою очередь, боль-

ше значения ключа правой вершины. Дерево должно быть сбалансиро-

ванным (длины всех путей от корня к листьям различаются не более

чем на 1). Только в таком случае достигается эффективность доступа.

3. Используется расстановка (хеширование),суть которой сводится к сле-

дующему. Определяется расстановочное поле (хеш-таблица) — мас-

сив фиксированного размера m, который будет заполняться ссылками

на группы компонентов исходного разреженного массива (записей но-

вого представления). Эти группы далее называются гроздями. На мно-

жестве всех возможных значений ключей определяется функция рас-

530

ГЛАВА 9. СТРУКТУРЫ ДАННЫХ

Индексы

…

Нет значения

Ключи

Значения

Рис. 9.8. Ключевое представление массива

становки

(хеш-функция) со значениями в множестве номеров гроздей

Термин ‘хеширование’ неудачен как в русском, так и в английском языке (переводится

примерно как “что-либо мелко порубленное, нарезанное”. Сам метод изобретен в СССР не-

зависимо от зарубежных аналогов и назван вполне логично расстановкой. Сопутствующие

понятия также получили вполне адекватные наименования. Однако после ужасного (в смы-

сле терминов) перевода замечательной книги Д. Гриса [26] расстановка стала замещаться

хешированием, и сегодня русский термин некоторым кажется старомодным.

Впервые этот метод (примитивный вариант) предложен Петерсоном [87]. А. П. Ершов

использовал собственный вариант метода в 1967 году в очень развитом для своего времени

трансляторе [32]. Хорошее изложение этого метода см. в [46].

Ключ

................................................

Ключ

1LL

Ключ

1LR

Ключ

1RR

Рис. 9.9. B-дерево

9.3. СТРУКТУРНЫЕ ТИПЫ

531

Расстановочное поле

1. Ссылка на гроздь 1

2. Ссылка на гроздь 2

Ссылка на гроздь 3 nil

…

m Ссылка на гроздь m

...

i11

i12

i1g1

...

i21

i22

Ключ

i2g2

...

Ключ

im1

Ключ

im2

Ключ

imgm

...

Ключ

i11

Ключ

i12

Ключ

i1g1

Ключ

i21

Ключ

i22

Нет значений с

соответствующ -и

ми ключами

Рис. 9.10. Расстановка (хеширование)

от 0 до m − 1 так, чтобы выполнялись условия перемешивания:

(a) для каждого значения ключа существует значение функции рас-

становки,

(b) множества всех возможных значений ключей разбивается на клас-

сы эквивалентных значений, у которых равны значения функции

расстановки, тем самым каждый класс задает свою гроздь,

статистически ожидаемого множества возможных значений ключей —

равномерность расстановки.

Устройство грозди может быть любым (массив, список). Их взаимное

размещение — также непринципиально (например, можно иметь пере-

мешанные в памяти грозди).

Наряду с B-деревьями, хеширование сейчас наиболее применимый об-

щий метод работы с ключевыми массивами. Поэтому возникают раз-

личные варианты и вырожденные случаи расстановки

(a) Многоуровневая расстановка. По существу, это двухступенчатый

доступ, т. е. работа с массивом массивов. Эффективность хеширо-

вания при этом резко падает. Используется, когда надо привлекать

внешнюю память.

532

ГЛАВА 9. СТРУКТУРЫ ДАННЫХ

(b) Расстановка по составному ключу. Два или более значения ин-

дексных полей — составной ключ — дают возможность практи-

чески всегда однозначно выделить значение массива. Можно счи-

тать, что здесь используются новые ‘большие’ значения. Здесь,

как правило, может нарушаться равномерность функции расста-

новки, тем не менее этот способ зачастую используется.

слу значений ключей. Нет нужды хранить значения ключей в ка-

честве компонентов наборов, представляющих абстрактный уро-

вень (они вычисляются однозначно). Если размер расстановочно-

го поля больше числа значений ключей, то имеет место бессмы-

сленная трата памяти, но этот вырожденный случай порою встре-

чается при использовании слишком мощного механизма для еще

не развившейся базы данных.

(d) Вырожденный случай 2: размер расстановочного поля равен еди-

нице. Это означает, что гроздь — весь массив, и он представляет-

ся списком, последовательностью и иным способом. Понятно, что

нет смысла в расстановочной функции, но иногда этот вырожден-

ный случай возникает на начальных этапах развития большой ба-

зы данных, в которой в дальнейшем без расстановки не обойтись.

4. Локально плотное представление. Оно используется в том случае,если

нам заранее известна глобальная информация о строении массива, что

часто случается в ходе больших вычислений с большими, но достаточ-

но регулярно организованными, матрицами.

Пусть имеется массив (матрица) следующего вида







A 0 B

0 C 0







(9.5)

Пусть W

, W

и H

, H

— числа элементов в ненулевых блоках

матрицы по горизонтали и вертикали, соответственно, элементы строк

и столбцов матрицы нумеруются с единицы. Тогда можно построить

9.3. СТРУКТУРНЫЕ ТИПЫ

533

следующую функцию:

F (k, 1) =











1, если(0 < k 6 W

)&(0 < l 6 H

)

2, если(W

+ W

< k 6 W

+ W

)&(0 < l 6 H

)

3, если(W

< k 6 W

+ W

)&(H

< l 6 H

+ H

)

exception

в остальных случаях

Она может рассматриваться в качестве функции расстановки для сле-

дующего программируемого доступа:

D [k, l]=

( case F(k, l) of

1 : D

[k, l];

2 : D

[k - W

- W

, l - H

];

3 : D

[k - W

, l - H

];

end)

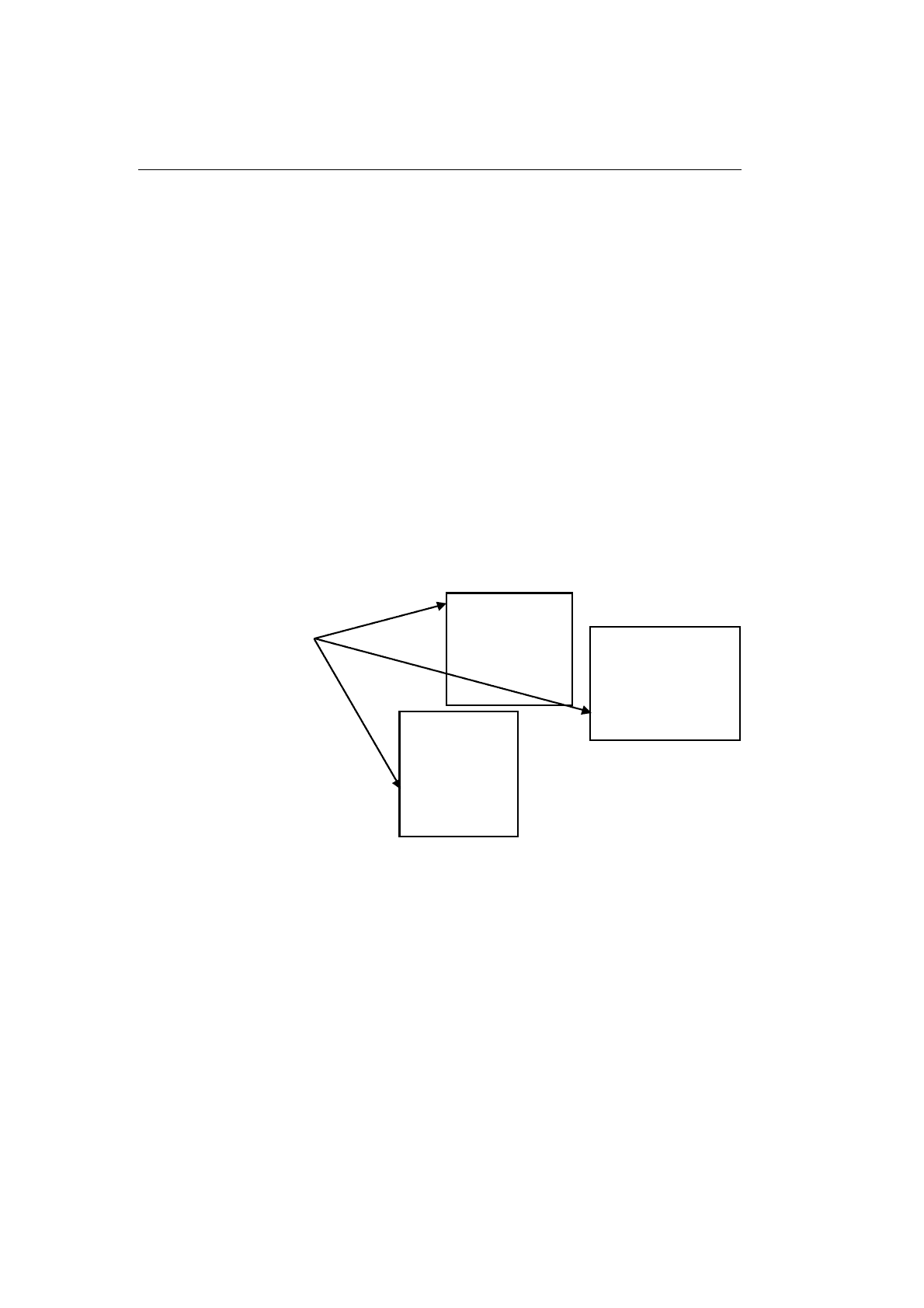
Ситуацию иллюстрирует рис. 9.11. В данном случае даже не потребо-

валось вводить расстановочное поле как структуру данных.

F ( k,l )

Рис. 9.11. Функция расстановки

Для всех вариантов массивов циклы всех видов допустимы, причем они ре-

ализуются достаточно эффективно. Также для всех размеров массивов не-

обходимо иметь функцию вычисления размера массива, более того, отсут-

ствие такой встроенной функции в стандартных языках программирования

является, пожалуй, одним из видов глупости, передающейся из поколение в

поколение.

534

ГЛАВА 9. СТРУКТУРЫ ДАННЫХ

9.3.5. Множества

Множество — это тип данных, значения которого представляют множе-

ства значений другого, ранее определенного типа, называемого базовым ти-

пом множества. Особенностью конструктора set of

является то, что опре-

деляемые с его помощью объекты в высшей степени зависят от количества

элементов в типе

и в принципе не содержат в себе в качестве компонент

значения базового типа. В данном отношении конструктор множеств отли-

чается от ранее рассмотренных нами конструкторов, которые интегрировали

значения базовых типов в определяемые ими структуры данных. Правда, са-

мое тупое из приходящих на ум представлений множества: перечень всех

элементов данного множества ({зн

, . . . , зн

} : T ) , — конечно, содержало

бы эти элементы. Но недостатки данного представления очевидны (тем не

менее, в одном из упражнений Вам предлагается найти случаи, когда такое

представление множества оптимально, и подумать, как его организовать в

таких случаях).

Другое представление множества естественно подсказывается изоморф-

ной алгебре множеств математической структурой функций M : T → {0, 1}.

Поскольку функция на конечном множестве, в свою очередь, то же самое, что

массив, то множество может быть представлено как массив булевских значе-

ний.

type

Set_T=

array

[T]

Boolean;

Просим извинения у любителей

C/C++/C#

, но примитивная логическая

структура этих языков не позволяет выразить данную идею столь же просто и

ясно. А в какие ловушки ведут попытки держаться слишком близко к деталям

реализации, мы уже видели.

Поскольку операции алгебры множеств над множествами A и B сводятся

к логическим операциям над значениями предикатов x ∈ A x ∈ B, вычисле-

ние объединений, пересечений и других операций булевой алгебры сводится

к циклу по всем элементам

с применением соотвествующих булевых опера-

ций к их элементам. Проверка равенства множеств, включения одного мно-

жества в другое и подсчет числа элементов множества также производится

Еще раз повторим, что изоморфизм математических понятий исключительно важен для

программиста, поскольку изоморфные структуры эквивалентны лишь с математической точ-

ки зрения, на практике они дают различные представления понятий.

Впрочем, так же в любой области человеческой деятельности. Попытка прямо достичь

цели чаще всего ведет в тупик, а победа, даже если она одержана, оказывается пирровой.