Murray J.D. Mathematical Biology: I. An Introduction

Подождите немного. Документ загружается.

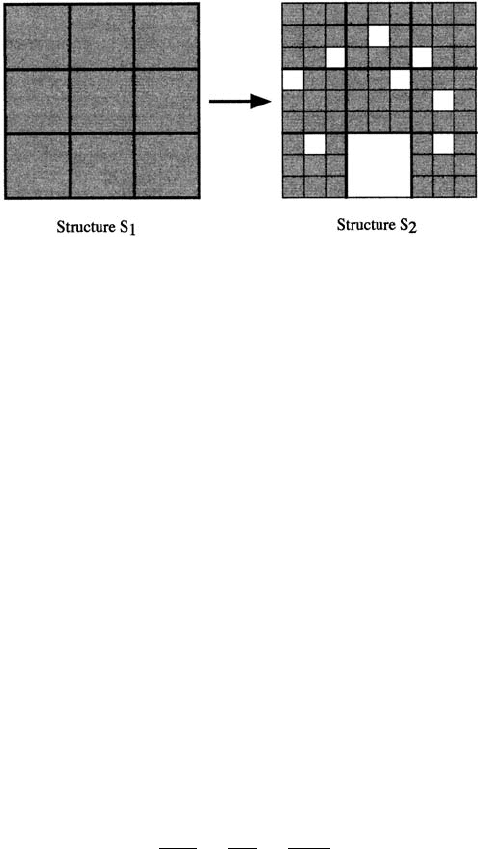
496 14. Use and Abuse of Fractals

Figure 14.8. Example of a nonself-similar fractal; see the text for a description of the generator.

the box size and plot ln N(r) against ln(1/r) for a range of r which gives a straight line

from which we can determine the gradient and hence D.

One problem with the box dimension is that it is not always easy to ﬁnd the mini-

mal cover; the situations reproduced in Figures 14.7(a) and 14.7(b) highlight this. The

method in Figure 14.7(a) is actually better than that in Figure 14.7(b). There are other

more complex and more accurate methods for calculating the fractal dimension, one of

the best of which is the Hausdorff dimension which uses sets of shapes with different

sizes. Although mathematically it gives a more accurate value for the dimension it is

very much harder to calculate. A simple illustrative example of a nonself-similar fractal

is shown in Figure 14.8. The generating rule consists of starting with a square divided

into nine equal small squares. Then choose one at random and remove it from the ﬁgure

to get the set S

. The remaining eight squares are then divided into nine equal smaller

squares and again one of the smaller squares in each box is selected at random and

discarded to obtain S

. The procedure is then repeated. This is a fractal structure with

qualitatively similar structures at each scale reduction and there is a kind of power scale

law in operation in that the individual surviving boxes certainly obey one. How do we

calculate the box dimension of this fractal structure? If we take the length of the side

of the original square to be unity then S

consists of N = 8 equal squares of side 1/3;

that is, the scale r = 1/3. The set S

consists of N = 8

squares with scale r = (1/3)

At the nth generation we have a structure S

with N = 8

squares with side of length

r = (1/3)

. From (14.9) we thus have the box dimension given by

D = lim

n→∞

ln 8

ln 3

ln 8

ln 3

3ln2

ln 3

= 1.893.

It is left as an exercise to calculate the box dimension of the nonself-similar fractal

obtained if a similar procedure to that used in Figure 14.8 is used with the Sierpinski

triangle in Figure 14.4.

14.4 Fractals or Space-Filling?

Let us now consider a biological situation involving cells such as that shown in Fig-

ure 14.1, or the volume occupied by the alveolar sacs in the lung organism or the typical

14.4 Fractals or Space-Filling? 497

(a) Summer (b) Winter

Figure 14.9. Ivy-covered wall in winter and summer. Is the branch structure in (a) fractal or is it space-ﬁlling

to optimise the leaf coverage (b) in the summer?

ivy covering of a wall as in Figure 14.9. Ideally, in the case of the lung, a major purpose

is to maximise the exchange of oxygen in the blood in the minimum amount of space.

In the case of the ivy the branches grow, it seems, so that they cover the available wall

space in the most efﬁcient space-ﬁlling way for the leaves to maximise the absorption of

sunlight and relevant gases to maximise the growth in the growth season. Such branch-

ing structures are widespread in Nature; see, for example, the many fractal-like forms

in Nature, reproduced in almost all books on fractals. In the case of the neuronal cells

in Figure 14.1 are they space-ﬁlling or are they fractal?

In the latter part of the 19th century and the beginning of the 20th there was con-

siderable interest in space-ﬁlling curves. What we mean by that is for any patch in a

given area there is a curve which touches each point of that patch. We come back to

the biological relevance shortly. To see how to construct such a curve we consider the

classical space-ﬁlling curve ﬁrst described by Hilbert in 1891. Figure 14.10 shows the

initial construction stages. Let us suppose the size of the line segments of the three-sided

ﬁgure in S

to be length 1. Then in the intermediate stage we have four such three-sided

ﬁgures with segment lengths of 1/2. We then join the four copies of S

with three lines

to get S

. The procedure is repeated to get S

using similar rotations and again joining

up the various quadrant curves with three other lines. So, S

has 16 copies of S

made

up of line segments of length 1/4. At stage S

we have 4n copies of S

made up of line

segments of length 1/2

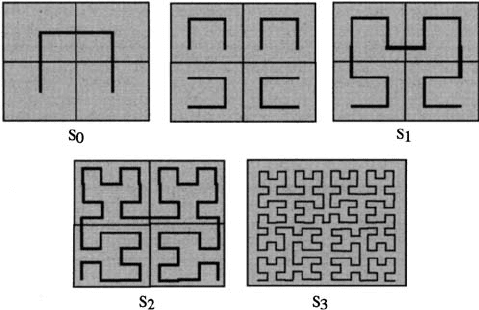
498 14. Use and Abuse of Fractals

Figure 14.10. The stepwise generation of the space-ﬁlling Hilbert curve. We start with the space and curve

, for the intermediate step in the second square and then join the four sets of lines to get S

,thenS

, S

and

so on. In the limit the curve passes through each point in the square.

The theory of space-ﬁlling curves gets quite technical mathematically but from a

biological viewpoint we do not need it. Suppose we have an organism which wants to

maximise its coverage of a given area or volume. One way to do this would be to have

a branching structure which obeyed local developmental branching rules to try and ﬁll

all the available space. The evolution of the curve in Figure 14.10 is one possible rule.

In fact is the regularity of such a branching pattern any better than a random oppor-

tunistic branching which has a normal topological dimension and is not fractal, not self-

similar nor has any other of the elegant geometric properties associated with fractals?

The branching pattern, fractal or otherwise, stops when the interbranch distance is at a

speciﬁc scale associated with the speciﬁc organism. This would result in a fairly even

mesh within which there is no further structure. In fact it would be counterproductive

to try to create a ﬁner structure than was necessary. By a careful analysis of retinal neu-

rons and vessels Panico and Sterling (1995) showed that neuronal and vascular patterns

showed no more self-similarity than the non-fractal controls they used. They concluded

that these biological patterns were not fractal but rather space-ﬁlling.

Although experiments might give rise to something that appears to be fractal, or

have a noninteger dimension, boundaries generally play a role in such measurements

and affect the subsequent log–log graphs. Whether or not something is fractal from

experimental measurements it must be clearly demonstrated that such boundary effects

can be ignored.

Caveat

It has frequently been suggested that if some pattern is fractal then we can infer some-

thing about the mechanism which generates it. The case most frequently cited is when

the pattern generated looks qualitatively similar to that in Figure 14.11 which is a typ-

ical pattern generated by diffusion limited aggregation. Diffusion limited aggregation

(DLA) is a diffusion process whereby particles exhibit a random walk behaviour and

14.4 Fractals or Space-Filling? 499

Figure 14.11. (a) Typical pattern generated by diffusion limited aggregation. (From Bassingthwaighte et

al. 1994 and reproduced with permission) (b) A typical amacrine cell from the central region of the rabbit

retina: scale bar is 100 µm (from Figure 14.1). (After Tauchi and Masland 1984) It is premature to draw any

conclusions as to the mechanism which forms (b) solely by visual comparison between it and the pattern in

(a).

when a particle comes into contact with another particle it sticks to it and can no longer

move. The process is usually started with a seed of stationary particles onto which re-

leased particles eventually diffuse. In this way a spatial pattern is dynamically formed

which is fractal in character. In this DLA example we can compute the fractal dimen-

sion theoretically; it is 1.7. We can, of course, also use the box dimension method, for

example, to compute it from the ﬁgure. Now compare the pattern in Figure 14.11 and

the cell patterns in Figure 14.1. It has often been suggested, for example, by Caserta et

al. (1990) and Schierwagen (1990), that the shape of neuronal cells may be determined

by a diffusion limited aggregative process. This is an unjustiﬁed conclusion to draw

from mere visual similarity.

Any model mechanism, such as diffusion limited aggregation, must be judged

against other biological spatial patterning generators by the experiments each of them

suggests. It is only by these that they can be differentiated. In the light of the easy

generation of hypothetical ferns, cauliﬂowers, trees and so on, it is easy to forget the

main purpose of studying pattern formation in biology, namely, to try and discover the

underlying biological processes which produce the spatial patterns.

This page intentionally left blank

Appendix A. Phase Plane Analysis

We discuss here, only very brieﬂy, general autonomous second-order ordinary differen-

tial equations of the form

= f (x, y),

= g(x, y). (A.1)

We present the basic results which are required in the main text. There are many books

which discuss phase plane analysis in varying depth, such as Jordan and Smith (1999)

and Guckenheimer and Holmes (1983). A good, short and practical exposition of the

qualitative theory of ordinary differential equation systems, including phase plane tech-

niques, is given by Odell (1980). Phase curves or phase trajectories of (A.1) are solu-

tions of

f (x, y)

g(x, y)

. (A.2)

Through any point (x

, y

) there is a unique curve except at singular points (x

, y

)

where

f (x

, y

) = g(x

, y

) = 0.

Let x → x −x

, y → y −y

; then, (0, 0) is a singular point of the transformed equation.

Thus, without loss of generality we now consider (A.2) to have a singular point at the

origin; that is,

f (x, y) = g(x, y) = 0 ⇒ x = 0, y = 0. (A.3)

If f and g are analytic near (0, 0) we can expand f and g in a Taylor series and,

retaining only the linear terms, we get

ax + by

cx +dy

, A =









(0,0)

(A.4)

which deﬁnes the matrix A and the constants a, b, c and d. The linear form is equivalent

to the system

502 Appendix A. Phase Plane Analysis

= ax +by,

= cx +dy. (A.5)

Solutions of (A.5) give the parametric forms of the phase curves; t is the parametric

parameter.

Let λ

and λ

be the eigenvalues of A deﬁned in (A.4); that is,



a − λ b

cd−λ



= 0 ⇒ λ

,λ

(a + d ±[(a +d)

−4detA]

1/2

). (A.6)

Solutions of (A.5) are then





= c

exp[λ

t]+c

exp[λ

t], (A.7)

where c

and c

are arbitrary constants and v

, v

are the eigenvectors of A correspond-

ing to λ

and λ

respectively; they are given by

= (1 + p

)

−1/2





, p

−a

, b = 0, i = 1, 2. (A.8)

Elimination of t in (A.7) gives the phase curves in the (x, y) plane.

The form (A.7) is for distinct eigenvalues. If the eigenvalues are equal the solutions

are proportional to (c

t) exp[λt].

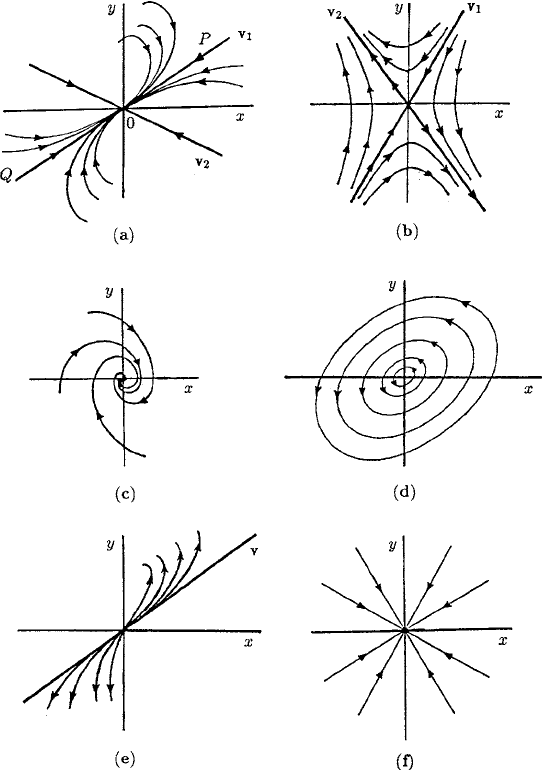
Catalogue of (Linear) Singularities in the Phase Plane

(i) λ

, λ

real and distinct:

(a) λ

and λ

have the same sign. Typical eigenvectors v

and v

are illustrated

in Figure A.1(a). Suppose λ

<λ

< 0. Then, from (A.7), for example, for

= 0, c

= 0,





= c

exp[λ

t],

so the solution in the phase plane simply moves along v

towards the origin

as t →∞in the direction shown in Figure A.1(a) — along PO if c

> 0

and along QO if c

< 0.

From (A.7) every solution tends to (0, 0) as t →∞since, with λ

< 0, exp[λ

t]=o(exp[λ

t]) as t →∞and so





∼ c

exp[λ

t] as t →∞.

Thus, close enough to the origin all solutions tend to zero along v

as shown

in Figure A.1(a). This is called a node (Type I) singularity. With λ

≤ λ

0 it is a stable node since all trajectories tend to (0, 0) as t →∞.Ifλ

> 0 it is an unstable node; here (x, y) → (0, 0) as t →−∞.

Appendix A. Phase Plane Analysis 503

Figure A.1. Typical examples of the basic linear singularities of the phase plane solutions of (A.4). (a) Node

(Type I): these can be stable (as shown) or unstable. (b) Saddle point: these are always unstable. (c)Spiral:

these can be stable or unstable. (d) Centre: this is neutrally stable. (e) Node (Type II): these can be stable or

unstable. (f) Star: these can be stable or unstable.

(b) λ

and λ

have different signs. Suppose, for example, λ

< 0 <λ

then

exp[λ

t]v

→ 0 along v

as t →∞while v

exp[λ

t]→0 along v

t →−∞.

There are thus different directions on v

and v

: the solutions near (0, 0)

are as shown in Figure A.1(b). This is a saddle point singularity. It is always

unstable: except strictly along v

any small perturbation from (0, 0) grows

exponentially.

504 Appendix A. Phase Plane Analysis

(ii) λ

,λ

complex: λ

,λ

= α ± iβ, β = 0. Solutions (A.7) here involve exp[αt]

exp[±iβt] which implies an oscillatory approach to (0, 0).

(a) α = 0. Here we have a spiral, which is stable if α<0 and unstable if

α>0; Figure A.1(c) illustrates a spiral singularity.

(b) α = 0. In this case the phase curves are ellipses. This singularity is called

a centre and is illustrated in Figure A.1(d). Centres are not stable in the

usual sense; a small perturbation from one phase curve does not die out

in the sense of returning to the original unperturbed curve. The perturbation

simply gives another solution. In the case of centre singularities, determined

by the linear approximation to f (x, y) and g(x, y), we must look at the

higher-order (than linear) terms to determine whether or not it is really a

spiral and hence whether it is stable or unstable.

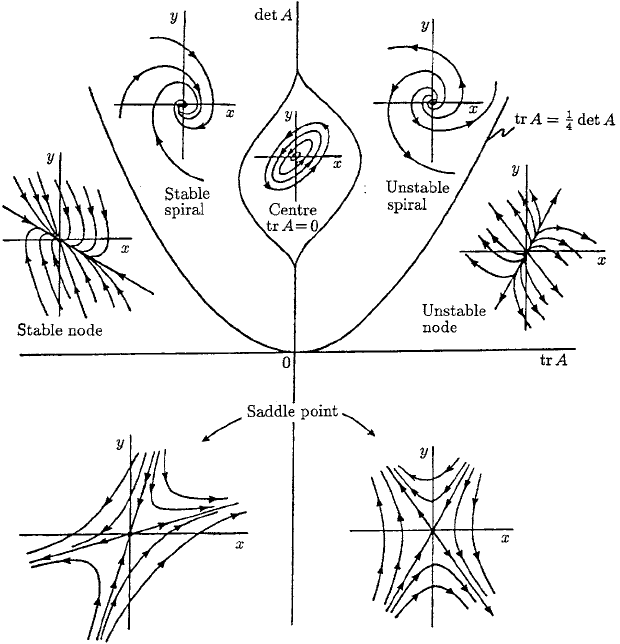
Figure A.2. Summary diagram showing how tr A and det A,whereA is the linearisation matrix given by

(A.4), determine the type of phase plane singularity for (A.1). Here det A = f

− f

,trA = f

+ g

where the partial derivatives are evaluated at the singularities, the solutions of f (x, y) = g(x, y) = 0.

Appendix A. Phase Plane Analysis 505

(iii) λ

= λ

= λ. Here the eigenvalues are not distinct.

(a) In general, solutions now involve terms like t exp[λt] and there is only one

eigenvector v along which the solutions tend to (0, 0).Thet in t exp[λt]

modiﬁes the solution away from (0, 0). It is called a node (Type II) singu-

larity, an illustration of which is given in Figure A.1(e).

(b) If the solutions do not contain the t exp[λt] term we have a star singularity,

which may be stable or unstable, depending on the sign of λ. Trajectories in

the vicinity of a star singularity are shown in Figure A.1(f).

The singularity depends on a, b, c and d in the matrix A in (A.4). Figure A.2

summarises the results in terms of the trace and determinant of A.

If the system (A.1) possesses a conﬁned set (that is, a domain on the boundary ∂ B

of which the vector (dx/dt, dy/dt) points into the domain) enclosing a single singular

point which is an unstable spiral or node then any phase trajectory cannot tend to the

singularity with time, nor can it leave the conﬁned set. The Poincar

e–Bendixson theorem

says that as t →∞the trajectory will tend to a limit cycle solution. This is the simplest

application of the theorem. If the sole singularity is a saddle point a limit cycle cannot

exist; see, for example, Jordan and Smith (1999) for a proof of the theorem, its general

application and some practical illustrations.