Murray J.D. Mathematical Biology: I. An Introduction
Подождите немного. Документ загружается.


156 5. Modelling the Dynamics of Marital Interaction
set of scores when W
t
= 0 and determine r
2
and a
2
in exactly the same way.
6
We can
now calculate the uninfluenced steady states and inertia of each partner.
Once we have estimated the uninfluenced component of the scores we can subtract
it from the scores at turn t + 1 to find the observed influenced component. That is, we
compute I
HW
(H
t
) = W
t+1
−r
t
W
t
− a
1
for each H
t
. For each value of the husband’s
score during the conversation there is likely to be a range of observed values of the
influence component due to noise in the data. To convert these into estimates for the
influence function I
HW
(H
t
) we simply average the observations for each of the hus-
band’s scores, H
t
. We then do the same for the husband’s influence function I
WH
(W
t
)
as a function of the wife’s score W
t
. In this way the raw influence data and the averaged
influence function can be plotted for each member of each couple.
To validate the estimation process, we then form a reconstructed conversation from
the model equations. We simply start by taking both people to be at their uninfluenced
state (non-integer values are allowed in this reconstruction) and then iterate forwards
for the approximately 80 turns of speech typically observed in 15 minutes. This is done
by computing the components separately and then summing to generate the next score.
The uninfluenced component is derived from linear equations like (5.2). The influenced
behaviour is computed by simply rounding the partner’s last score to the nearest integer
and reading off the influence from that person’s average influence function referred
to above. The reconstructed conversation therefore lacks any randomness; we do not
pretend that this ‘expected’ conversation would ever be observed in practice. Rather, it
represents an underlying trend.
5.4 Steady States and Stability
For each couple we plot the model’s null clines in the (W
t
,H
t
) phase plane. Here, a point
in the plane is the pair of numbers representing the husband’s and the wife’s scores for a
particular interaction (a two-turn unit). As time progresses, this point moves, and traces
out a trajectory in phase space. We are interested in the stability of the steady states,
the points where the null clines intersect. These steady states are clearly very important
since they provide crucial information on the state of the marriage, and on guiding
potential repair therapy. Since the null clines are obtained from the data we determine
the steady states by looking for the intersections of the null clines in the usual way.
Here, however, we have coupled discrete equations and so must consider what we mean
by a null cline for such equations. Recall what a null cline is from Chapter 3. They are
curves in the phase plane where values stay the same over time. A person’s null cline is
a function of their partner’s last score and gives the value of their own score when this is
unchanged over one iteration, in other words when W
t+1
= W
t
and H
t+1
= H
t
.Aswe
saw in Chapter 3, plotting null clines provides a simple graphical means of determining
6
If these zero influence points were rare, it would be hard to obtain accurate estimates for the model
parameters since the confidence intervals around these parameters would be large. While it seems like a
strong assumption, the assumption that zero scores have zero influence is arbitrary. We could assume nonzero
influences, make these additional parameters, and estimate these parameters as well. In fact, an asymmetry in
these parameters would be theoretically interesting in characterizing a couple’s interaction. In the interest of
parsimony, we took these parameters to be zero.

5.4 Steady States and Stability 157
steady states. From (5.4) and (5.5) the null clines N
HW
and N
WH
are given respectively
by
N
HW
: W(H
t
) =
I
HW
(H
t
) + a
(1 −r
1
)
, N
WH
: H(W
t
) =
I
WH
(W
t
) + b
(1 −r
2
)
. (5.6)
These equations are simply the influence functions respectively translated by the con-
stants a and b and scaled by the constants 1 − r
1
and 1 − r
2
. Steady states are then
given by the intersections of the null clines, since, by definition, if the (W
t
, H
t
) started
at such a point then it would stay there. The concept is exactly the same as for differen-
tial equations. Also, just as for these, the stability of the steady states provides crucial
information. Since we have not specified the functional form of the influence functions
analytically, we proceed qualitatively.
However, it is instructive to discuss what would happen if we settled on a functional
form for the influence functions. For example, suppose we consider I
HW
(H
t
) to be sim-
ilar to the piecewise linear sigmoidal form illustrated in the upper figure in Figure 5.2
with a similar form for I
WH
(H
t
). This assumption is reasonable since it presumes two
thresholds of influence and that the influence is bounded in both negative and positive
ranges. The pair of equations (5.6) can easily be solved graphically by simply plot-
ting the influence functions and translating and stretching them according to (5.6). The
steady states are given in the usual way by the points of intersections of the null clines.
These steady states, the intersection points, are where both the wife’s and the hus-
band’s scores remain constant on consecutive turns of speech. These points we call the
influenced steady states. If a couple were to reach one of these states during a conver-
sation, whether or not they remain there with each partner scoring the same on each
of their future turns of speech depends on the stability of the steady states. Although
there may be several influenced steady states (depending on the influence functions and
the uninfluenced parameters), to date we have usually found only one. Figure 5.3 is a
possible null cline scenario in which there are 5 possible steady, influenced, states. With
the typical form in the upper figure in Figure 5.2, the null clines, denoted by N
HW
and
N
WH
, are illustrated in Figure 5.3.
We analyse the stability of the steady states below. We are familiar with the concept
of stability and instability from the models we have discussed in earlier chapters. The
concepts are exactly the same here except that we are dealing with RCISS scores. If
a theoretical conversation were continued for some time, then pairs of scores would
approach a stable steady state and move away from an unstable one. Although it is
theoretically possible to have periodic behaviour we do not discuss this possibility here.
Each stable steady state has a basin of attraction.
Let us now examine the stability of the steady states of W
S
, H
S
of (5.4) and (5.5).
Intheusualwayweset
W
t
= W
S
+w
t
H
t
= H
S
+h
t
,
(5.7)
where |w
t
| and |h
t
| are small. Substituting these into (5.4) and (5.5), expanding in a
Taylor series and keeping only linear terms, we get:
W
t
H
t
NULL CLINES
N
WH
(husband’s null cline)
N
HW
(wife’s
null cline)
(a)
W
t
H
t
NULL CLINES
N
WH
(husband’s null cline)
(b)
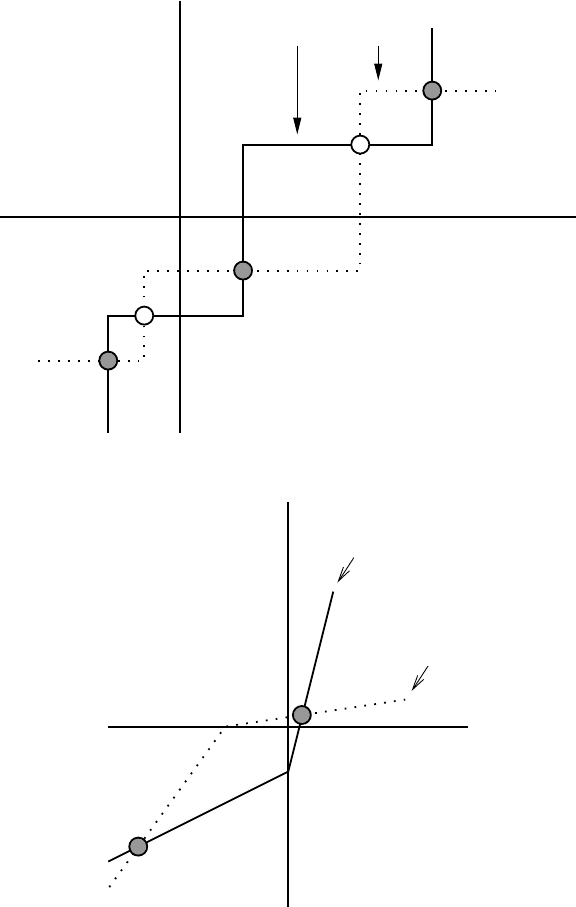
Figure 5.3. The null clines determine the steady states for typical piecewise linear forms of the influence
functions as in Figure 5.2(a). The null clines have the same general shape as the influence function but are
translated and stretched (see (5.6)). When the null clines are plotted against their respective axes, the steady
states of the system are the points of intersection. In (a) the intersection of the two null clines shows that 5
steady states are possible with this form of the influence function; note that the influence functions of the wife
and husband are plotted in mirror-image relationship. The stability of these is crucial. In (b) there are only 2
possible steady states (both of them cannot be stable). In (a) the stable steady states (filled circles) alternate
with unstable steady states as we show in the text. Depending on the form of the interaction functions there
are other possibilities.
158

5.4 Steady States and Stability 159
W
t+1
= W
S
+w
t+1
= I
HW
(H
S
+h
t
) +r
1
(W
S
+w
t
) +a
≈ I
HW
(H
S
) + h
t
I
HW
(H
S
) +r
1
(W
S
+w
t
) +a,
(5.8)
where I
HW
(H
S
) is dI
HW
(H
t
)/dH
t
evaluated at the steady state H
S
and similarly for
I
WH
(W
S
).ButI
HW
(H
S
) + r
1
W
S
+ a = W
S
by definition of the steady state W
S
,so,
the last equation simplifies to
w
t+1
= r
1
w
t
+ I
HW
(H
S
)h
t
. (5.9)
Similarly, with the husband’s equation (5.5), we get
h
t+1
= r
2
h
t
+ I
WH
(W
S
)w
t+1
, (5.10)
which on substituting for w
t+1
gives, together with (5.9), the following system of linear
difference equations,
w
t+1
h
t+1
=
r
1
I
HW
(H
S
)
r
1
I
WH
(W
S
) r
2
+ I
WH
(W
S
)I
HW
(H
S
)
w
t
h
t
= M
w
t
h
t
, (5.11)
where M, defined by (5.11), is the stability matrix.
In the usual way we look for solutions of (5.11) in the form
w
t
h
t
∝ λ
t
(5.12)
and determine the λ. Since the system is second-order, there are in general two λ’s.
Stability is then obtained if the magnitude of both λ’s (which can be positive or negative)
is less than 1, since then the perturbation solutions of the form (5.12) decay as t increases
and eventually tend to zero.
Substituting (5.12) into (5.11) requires the λ to be solutions of the determinant
r
1
−λ I
HW
(H
S
)
r
1
I
WH
(W
S
) r
2
+ I
WH
(W
S
)I
HW
(H
S
) −λ
= 0, (5.13)
that is
λ
2
−(r
1
+r
2
+ I
WH
I
HW
)λ +r
1
r
2
= 0
and so the λ’s are
λ
1
,λ
2
=
1
2
(r
1
+r
2
+ I
WH
I
HW
) ±
(r
1
+r
2
+ I
WH
I
HW
)
2
−4r
1
r
2
1/2
. (5.14)

160 5. Modelling the Dynamics of Marital Interaction
The solutions for the perturbations w
t
and h
t
are then given by
w
t
h
t
= Aλ
t
1
+Bλ
t
2
, (5.15)
where A, B are constant column matrices. If |λ
1
| > 1or|λ
2
| > 1, then w
t
and h
t
will
grow with each increase in t and the steady state is linearly unstable. Stability therefore
requires
−1 <λ
1
< 1and − 1 <λ
2
< 1, (5.16)
in which case w
t
and h
t
tend to zero as t increases.
We now substitute the expressions for λ
1
and λ
2
from (5.14) into (5.16) to obtain the
conditions on r
1
, r
2
, I
HW
(H
S
) and I
WH
(W
S
) for stability of the steady state W
S
, H
S
.
Although we can do this for general r
1
and r
2
, there is little point since we know that
0 ≤ r
1
< 1and0≤ r
2
< 1. If either were greater than 1 there would be no uninfluenced
steady state, since from (5.3), it (the P
t
) would get infinitely large for t large. So with
these practical restrictions, dictated by the model (and actually confirmed by the data),
we need consider only nonnegative r
1
< 1andr
2
< 1.
The stability condition is then given by requiring the square bracket in (5.14) to be
less than 2. A little algebra shows that we must have at the steady state W
S
, H
S
,
I
WH
(W
S
)I
HW
(H
S
)<(1 −r
1
)(1 −r
2
), (5.17)
where I
WH
(W
S
) = dI
WH
(W
t
)/dW
t
evaluated at the steady state W
S
, H
S
and similarly
for I
HW
(H
S
). So, if we want to assess the stability of a steady state, we have to evaluate
the derivatives of the influence functions and use (5.17).
In general, we can say that steep influence functions and high inertia, the r-param-
eters, are destabilizing for a steady state. Recall that high inertia means r close to 1. For
example, if each influence function has a slope greater than one then the steady state
would be unstable irrespective of inertia values. This agrees with our intuitive expec-
tations if we interpret instability as the amplification of small perturbations. Influence
is a measure of the effect that one partner has on the other and is so large that changes
in influence will result in amplification, or mutual instability. On the other hand, even
couples with relatively flat (low derivative) influence functions can have unstable steady
states if either of the partners’ inertia is high (close to 1).
Condition (5.17) can be interpreted graphically. The null clines could intersect ei-
ther as shown in Figure 5.4(a) or (b). From (5.4) and (5.5), the equations for the null
clines are (5.6); namely,
N
HW
: W =
I
HW
(H) +a
(1 −r
1
)
, N
WH
: H =
I
WH
(W) + b
(1 −r
2
)
, (5.18)
5.4 Steady States and Stability 161
(a)
unstable
(b)
stable
W
W
H
H
N
WH
(H)
N
WH
(H)
N
HW
(W)
N
HW
(W)
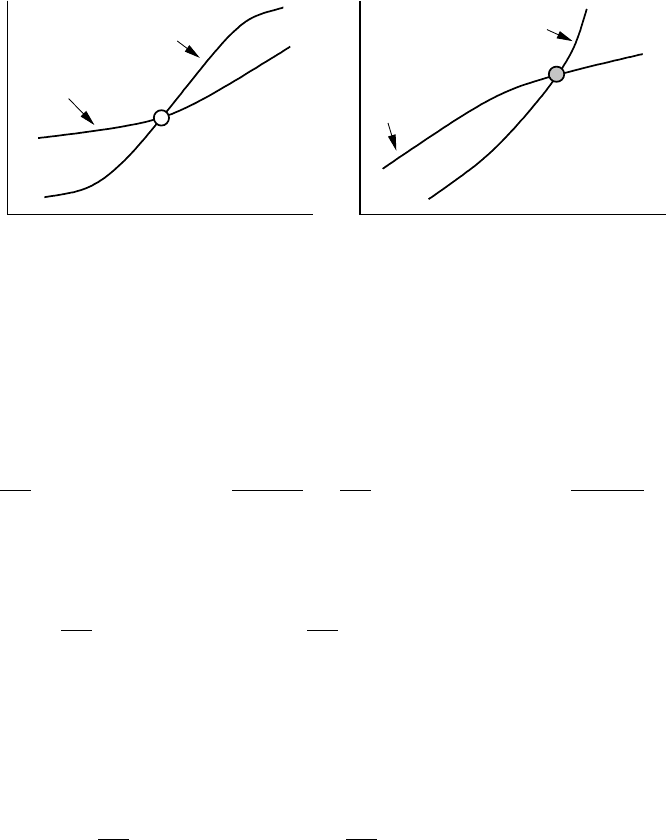
Figure 5.4. Null clines and the stability of steady states for the marriage model. Steady states correspond to
points at which the null clines intersect. The stability of a steady state can be determined graphically (see text
for details): when the null clines intersect as is shown in (a), the steady state is unstable; when they intersect
as is shown in (b), the steady state is stable. H = Husband; W = Wife.
where N
HW
is the wife’s null cline and N
WH
is the husband’s. If we now take the
derivatives of these, respectively, with respect to H and W,weget
dW
dH
On wife’s
null-cline, N
HW
=
I
HW
(H)
1 −r
1
,
dH
dW
On husband’s
null-cline, N
WH
=
I
WH
(W)
1 −r
2
.
So, the stability condition (5.17) becomes simply
dH
dW
On husband’s
null-cline, N
WH
,
at W
S
, H
S
×
dW
dH
On wife’s
null-cline, N
HW
,
at W
S
, H
S
< 1
as the conditions on the gradients at a steady state. With the axes chosen, namely, W the
vertical axis and H the horizontal one, the last expression guaranteeing stability can be
written as
dW
dH
On wife’s
null-cline, N
HW
,
at W
S
, H
S
<
dW
dH
On husband’s
null-cline, N
WH
,
at W
S
, H
S
. (5.19)
So, all we need to do is evaluate the gradients and stability or instability is immediately
obtained at each steady state. Let us now consider some examples using the null clines
and steady states in Figures 5.4(a) and 5.4(b).
Consider first the positive steady state in Figure 5.4(a). By inspection, the gradient
on the wife’s null cline is greater than that on the husband’s null cline. So the condition
(5.19) is not satisfied and thus the positive steady state is unstable. If we now look at
Figure 5.4(b) we see that condition (5.19) is satisfied so the steady state is stable.
162 5. Modelling the Dynamics of Marital Interaction
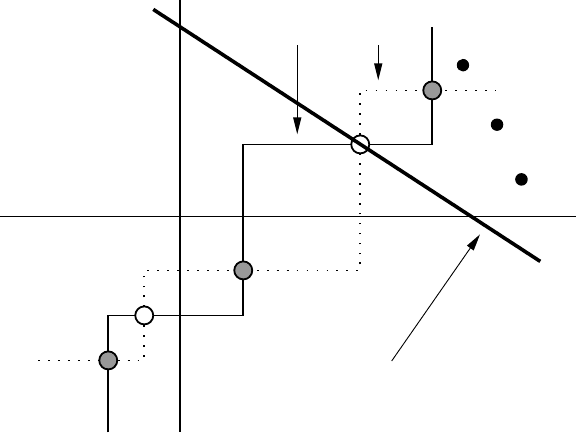
Now consider Figure 5.3. At the open circle steady states the gradients are infinite
so the stability criterion (5.19) is violated, so these are unstable steady states. On the
other hand, the filled circles have zero gradients and (5.19) is satisfied so they are stable.
As we now should expect, the steady states alternate in stability and instability. In con-
clusion then, under these conditions on the inertia parameter (0 ≤ r
1
< 1, 0 ≤ r
2
< 1)
we can graphically determine not only the location of the steady states but also their
stability. A simple corollary to this null cline intersection stability condition is that the
stable and unstable steady states must alternate; that is, any two stable steady states are
separated by an unstable one and vice versa. If we assume that the influence functions
are monotonic increasing functions then the steady states can be ordered. By this we
mean that the steady state values, W
S
and H
S
, will both increase as we move from one
steady state to the next. If we assume, as is reasonable, that influence functions satu-
rate, then the highest and lowest steady state are clearly stable (they must intersect as in
Figure 5.4(b) (see also Figure 5.5): there must be an odd number of steady states that
alternate between stable and unstable, with the first and last being stable. In all of the
above, by stability we mean linear stability since it is clear that we can perturb a stable
steady state so that it will fall in the basin of attraction of another stable steady state.
W
t
H
t
NULL CLINES
(W
3
, H
3
)
(W
2
, H
2
)
(W
1
, H
1
)
Curve separating two basins
of attraction (the ‘separatrix’)
N
HW
N
WH
Figure 5.5. Null clines and a typical sequence of theoretical RCISS scores in the case of three steady states.
The solid null cline is the husband’s influence on the wife, while the dotted null cline is the wife’s influence on
the husband. Two stable steady states (large filled circles) are separated by an unstable steady state (large open
circle). A possible sequence of scores is shown approaching the positive steady state (small filled circles).
Each point corresponds to a consecutive pair of scores (W
t
, H
t
). Both stable steady states have a basin of
attraction consisting of points starting from which a sequence of theoretical RCISS scores will approach the
steady state in question. The separatrix curve delineating the basins of attraction is shown as a dotted line.
Pairs of scores gradually approach one of the positive stable states; the long term behaviour of the sequence
is therefore dependent upon the basin of attraction in which the initial pair of scores lies.

5.4 Steady States and Stability 163
To determine the basins of attraction of each stable steady state we have to deter-
mine the separatrices. This, as in most differential equation systems, has to be done
numerically. However, at least in the neighbourhood of each stable steady state we can
get some idea of the strength of attraction. With differential equations, one way to mea-
sure the strength of attraction of a steady state is to construct an energy type of function,
such as a Liapunov function. This is not always easy. For difference equation systems,
such as we have in the marriage interaction model here, there is, as far as we know, no
such equivalent. However, in the neighbourhood of a stable steady state, essentially in
the linear neighbourhood, we can give a parameter which provides at least some com-
parative basis for the strength of the stable steady state attractor.
The linear perturbation solutions w
t
and h
t
about a steady state are given by (5.15).
For stable steady states, |λ
1
| < 1and|λ
2
| < 1. To be specific suppose |λ
2
| < |λ
1
|.
As t increases the term involving λ
t
1
eventually dominates the solution. The closer |λ
1
|
is to 1, the slower the perturbations about the steady state die out and hence the weaker is
the attraction of the steady state. So, a measure, albeit a linear measure, of the strength,
S, of an attracting stable steady state is given by
S = maximum(|λ
1
| and |λ
2
|).
The closer S is to unity, the weaker is the attractor, or alternatively the closer S is to zero
the stronger the attractor. This result may have considerable importance. For example,
one effect of marital therapy may be to strengthen the positive attractor and weaken the
negative attractor; we discuss the application of the theory to marital therapy below.
An example of a hypothetical sequence of scores is shown in Figure 5.5 approach-
ing the more positive steady state. This theoretical conversation would be constructed
by simply iterating equations (5.4) and (5.5) from some initial pair of scores. The po-
tential existence of multiple stable steady states each with its own basin of attraction has
practical implications. The model suggests that the final outcome (positive or negative
trend) of a conversation could depend critically on the opening scores of each partner.
Where one begins in the phase space is determined by the couple’s actual initial con-
ditions, in other words which basin of attraction you start in. We have generally found
that the end points can depend critically on starting values.
7
An observed or a ‘reconstructed’ conversation can be represented in the phase plane
as a series of connected points. In addressing the issue of stability of the steady states,
we are asking whether the mathematical equations imply that the reconstructed series
will approach a given steady state. Analytically, we ask the question of where a steady
state will move once it is slightly perturbed from its position. Of course the theoretical
behaviour of the model in response to perturbations of the steady states is only possible
once we have a functional form for the influence functions. For example, as we have
7
Notwithstanding what has been termed the punctuation fallacy, in which where one starts in an interaction
is quite arbitrary, we have found in practice that the couple’s starting values of the interaction appear to be
very important in determining the couple’s eventual trajectory. We have considered modifying the influence
functions to include a repair component, whose existence would be capable of moving a couple from a
negative to a positive steady state. If there were a repair component operating, the cumulative graph could
look like a check mark, starting downward and then changing direction. Unfortunately, this occurred in our
data for only 4% of the cases. Perhaps effective marital therapy might add such a repair component to the
influence functions. This is discussed in detail by Gottman et al. (2002).
164 5. Modelling the Dynamics of Marital Interaction
noted, for the sigmoidal influence function, we can have 1, 3 or 5 steady states (see
Figure 5.3). With the latter, from the null cline plot (see Figure 5.3) we can see that
there are 3 stable and 2 unstable states.
What does it mean practically for there to be multiple steady states? These are all
possible states for a particular couple. Even if we only observe the couple near one
of them in our study, all are possible for this couple, given the equations. Each stable
steady state will have a basin of attraction. This is the set of starting points from which
a reconstructed time series will approach the steady state in question. If there is a single
steady state, then its basin of attraction is the whole plane—that is, no matter what the
initial scores were, the sequence would approach this one steady state. We have found
this tendency toward a single steady state to be the usual situation in our data. If, on
the other hand, there are two stable steady states (and, necessarily, one unstable one)
the plane will be divided into two regions, the basins of attraction (see Figure 5.5). If
the scores start in the first stable steady state’s basin of attraction, then, in time, the se-
quence of scores will approach that steady state. The same goes for the second steady
state and its basin of attraction. This situation is depicted in Figure 5.5. The couple be-
gins at the point (W
1
, H
1
) in phase space, next moves to the point (W
2
, H
2
), and next
moves to the point (W
3
, H
3
), and so on, heading for the large black dot that represents
the stable steady state intersection of the two null clines. The eventual trend that the
conversation follows can be highly dependent on the initial conditions. Thus, high in-
ertia, high influence couples (who are more likely to have multiple steady states) could
potentially exhibit a positive conversation on one day and yet not be able to resolve
conflict on another. The only difference could be the way the conversation began (their
initial RCISS scores). The influence functions and uninfluenced parameters would be
identical on each day. This discussion makes concrete the general systems theory no-
tion of first-order (or more superficial, surface structure) change and second-order (or
more meaningful, deeper structure) change (Watzlawick et al. 1967). In our model, first-
order change means that the steady states may change but not the influence functions;
second-order change would imply a change in the influence functions as well.
5.5 Practical Results from the Model
Influence Functions
Note that influence functions are arbitrarily attributed to the influencer, although we
recognize that the influenced spouse will also play a part in determining the influence.
As a rough approximation to the shape of the influence functions, obtained from the
data by least squares, we used the two-slope function and computed the slope of the
influence function separately for negative and positive value of the partner’s behaviour.
The horizontal axis represented the range of positivity or negativity in each group. Only
data close to the natural steady state for each group could be trusted to avoid infrequent
numbers of instances of RCISS values within a group. This means that we get more
reliable information for regulated couples in the positive ranges and for nonregulated
couples in the negative ranges of the horizontal axis. Figure 5.6 is a summary of the
empirically obtained functions for five groups of couples, the three stable marriages
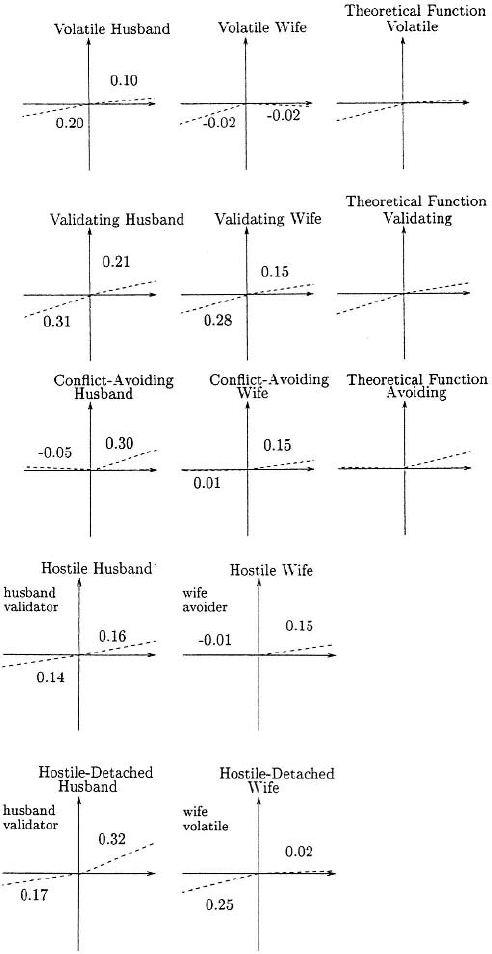
5.5 Practical Results from the Model 165
Figure 5.6. Empirically obtained influence functions using a two-slope bilinear functional form for the influ-
ence function. The top three marriage types all fall into the category of low risk marriages and it is possible
to determine a theoretical influence function for each type of marriage. The bottom two belong to the high
risk category of marriages: note the mismatch in slopes. For example, in the Hostile-Detached graphs the hus-
band has an influence function characteristic of validator husbands while the wife has an influence function
characteristic of avoiding wives. Because of this mismatch it is not possible to determine theoretical influence
functions for these marriage types. (From Cook et al. 1995)
