Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics
Подождите немного. Документ загружается.

consisting of a system and that portion of the surroundings affected by the system as it
undergoes a process. Since all energy and mass transfers taking place are included within
the boundary of the enlarged system, the enlarged system is an isolated system.
An energy balance for the isolated system reduces to
¢E
4
isol
5 0 (6.29a)
because no energy transfers take place across its boundary. Thus, the energy of the
isolated system remains constant. Since energy is an extensive property, its value for
the isolated system is the sum of its values for the system and surroundings, respec-
tively, so Eq. 6.29a can be written as
¢E
4
s
y
stem
1 ¢E
4
surr
5 0 (6.29b)
In either of these forms, the conservation of energy principle places a constraint on
the processes that can occur. For a process to take place, it is necessary for the energy
of the system plus the surroundings to remain constant. However, not all processes
for which this constraint is satisfied can actually occur. Processes also must satisfy the
second law, as discussed next.
An entropy balance for the isolated system reduces to
¢S4
isol
5
#
2
1
a
d
Q
T
b
0
b
1 s
isol
or
¢S
4
isol
5 s
isol
(6.30a)
where s
isol
is the total amount of entropy produced within the system and its sur-
roundings. Since entropy is produced in all actual processes, the only processes that
can occur are those for which the entropy of the isolated system increases. This is
known as the increase of entropy principle. The increase of entropy principle is some-
times considered an alternative statement of the second law.
Since entropy is an extensive property, its value for the isolated system is the sum of
its values for the system and surroundings, respectively, so Eq. 6.30a can be written as
¢S
4
s
y
stem
1 ¢S
4
surr
5 s
isol
(6.30b)
Notice that this equation does not require the entropy change to be positive for both
the system and surroundings but only that the sum of the changes is positive. In either
of these forms, the increase of entropy principle dictates the direction in which any
process can proceed: Processes occur only in such a direction that the total entropy
of the system plus surroundings increases.
We observed previously the tendency of systems left to themselves to undergo
processes until a condition of equilibrium is attained (Sec. 5.1). The increase of
entropy principle suggests that the entropy of an isolated system increases as the state
of equilibrium is approached, with the equilibrium state being attained when the
entropy reaches a maximum. This interpretation is considered again in Sec. 14.1, which
deals with equilibrium criteria.
Example 6.5 illustrates the increase of entropy principle.
6.8 Directionality of Processes 303
increase of entropy
principle
Quenching a Hot Metal Bar
c c c c EXAMPLE 6.5 c
A 0.8-lb metal bar initially at 19008R is removed from an oven and quenched by immersing it in a closed tank
containing 20 lb of water initially at 5308R. Each substance can be modeled as incompressible. An appropriate
constant specific heat value for the water is c
w
5 1.0 Btu/lb
?
8R, and an appropriate value for the metal is c
m
5
0.1 Btu/lb
?
8R, Heat transfer from the tank contents can be neglected. Determine (a) the final equilibrium tem-
perature of the metal bar and the water, in 8R, and (b) the amount of entropy produced, in Btu/8R.
c06UsingEntropy.indd Page 303 5/26/10 2:40:54 PM user-s146c06UsingEntropy.indd Page 303 5/26/10 2:40:54 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
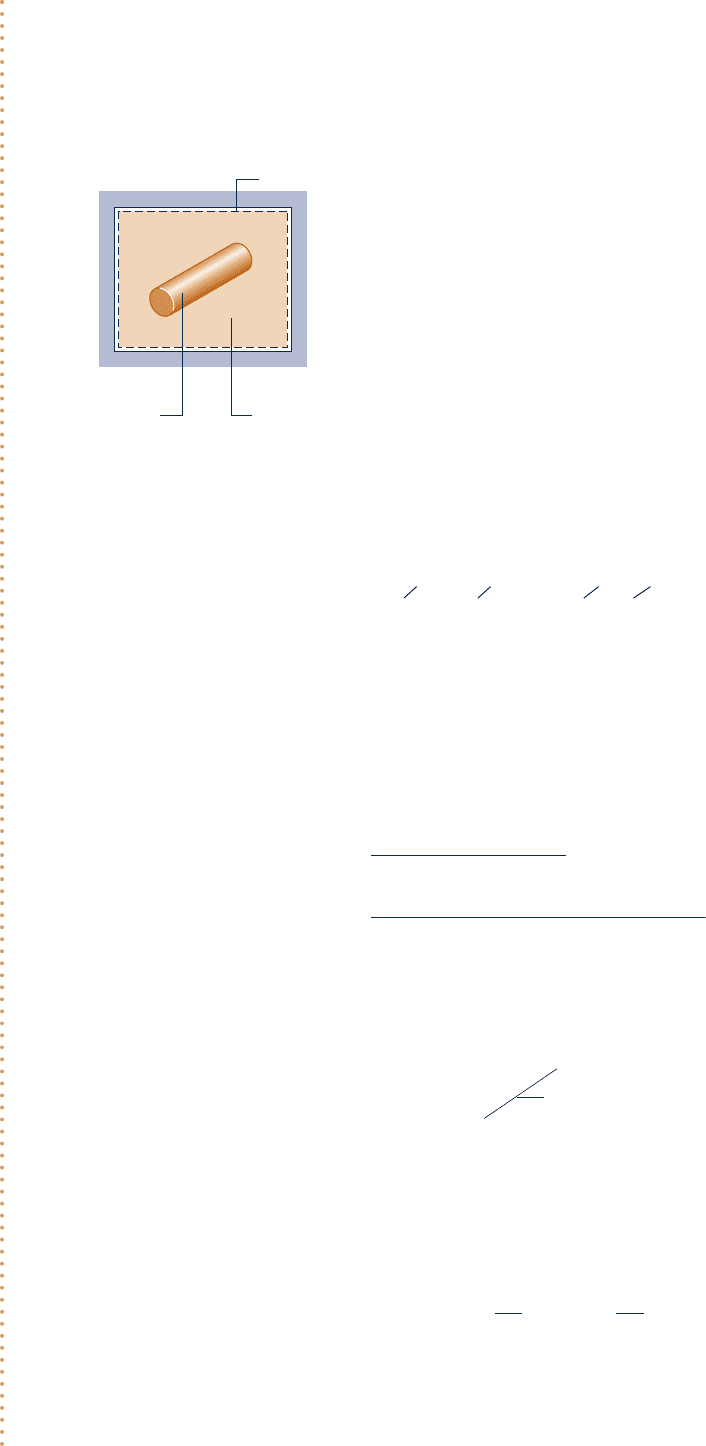
304 Chapter 6 Using Entropy
SOLUTION
Known:
A hot metal bar is quenched by immersing it in a closed tank containing water.
Find: Determine the final equilibrium temperature of the metal bar and the water, and the amount of entropy
produced.
Schematic and Given Data:
Analysis:
(a)
The final equilibrium temperature can be evaluated from an energy balance for the isolated system
¢KE
0
1 ¢PE
0
1 ¢U 5 Q
0
2 W
0
where the indicated terms vanish by assumptions 2 and 3. Since internal energy is an extensive property, its value for
the isolated system is the sum of the values for the water and metal, respectively. Thus, the energy balance becomes
¢U4
water
1 ¢U4
metal
5 0
Using Eq. 3.20a to evaluate the internal energy changes of the water and metal in terms of the constant specific heats
m
w
c
w
1T
f
2 T
wi
21 m
m
c
m
1T
f
2 T
mi
25 0
where T
f
is the final equilibrium temperature, and T
wi
and T
mi
are the initial temperatures of the water and metal,
respectively. Solving for T
f
and inserting values
T
f
5
m
w
1c
w
y
c
m
2T
wi
1 m
m
T
mi
m
w
1c
w
y
c
m
21 m
m
5
120 lb2110215308R21 10.8 lb2119008R
2
120 lb211021 10.8 lb2
5 5358R
(b) The amount of entropy production can be evaluated from an entropy balance. Since no heat transfer occurs
between the isolated system and its surroundings, there is no accompanying entropy transfer, and an entropy
balance for the isolated system reduces to
¢S 5
#
2
1
a
dQ
T
b
b
0
1 s
Entropy is an extensive property, so its value for the isolated system is the sum of its values for the water and
the metal, respectively, and the entropy balance becomes
¢S4
water
1 ¢S4
metal
5 s
Evaluating the entropy changes using Eq. 6.13 for incompressible substances, the foregoing equation can be
written as
s 5 m
w
c
w
ln
T
f
T
wi
1 m
m
c
m
ln
T
f
T
mi
Engineering Model:
1.
The metal bar and the water within the tank form a system, as
shown on the accompanying sketch.
2. There is no energy transfer by heat or work: The system is
isolated.
3. There is no change in kinetic or potential energy.
4. The water and metal bar are each modeled as incompressible
with known specific heats.
Fig. E6.5
System boundary
Water:
= 530°R
= 1.0 Btu/lb·°R
= 20 lb
T
wi
c
w
m
w
Metal bar:
= 1900°R
= 0.1 Btu/lb·°R
= 0.8 lb
T
mi
c
m
m
m
c06UsingEntropy.indd Page 304 5/26/10 5:20:26 PM user-s146c06UsingEntropy.indd Page 304 5/26/10 5:20:26 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
6.8.2
Statistical Interpretation of Entropy
Building on the increase of entropy principle, in this section we
introduce an interpretation of entropy from a microscopic perspec-
tive based on probability.
In statistical thermodynamics, entropy is associated with the notion
of microscopic disorder. From previous considerations we know that
in a spontaneous process of an isolated system, the system moves
toward equilibrium and the entropy increases. From the microscopic
viewpoint, this is equivalent to saying that as an isolated system moves
toward equilibrium our knowledge of the condition of individual par-
ticles making up the system decreases, which corresponds to an
increase in microscopic disorder and a related increase in entropy.
We use an elementary thought experiment to bring out some
basic ideas needed to understand this view of entropy. Actual micro-
scopic analysis of systems is more complicated than the discussion
given here, but the essential concepts are the same.
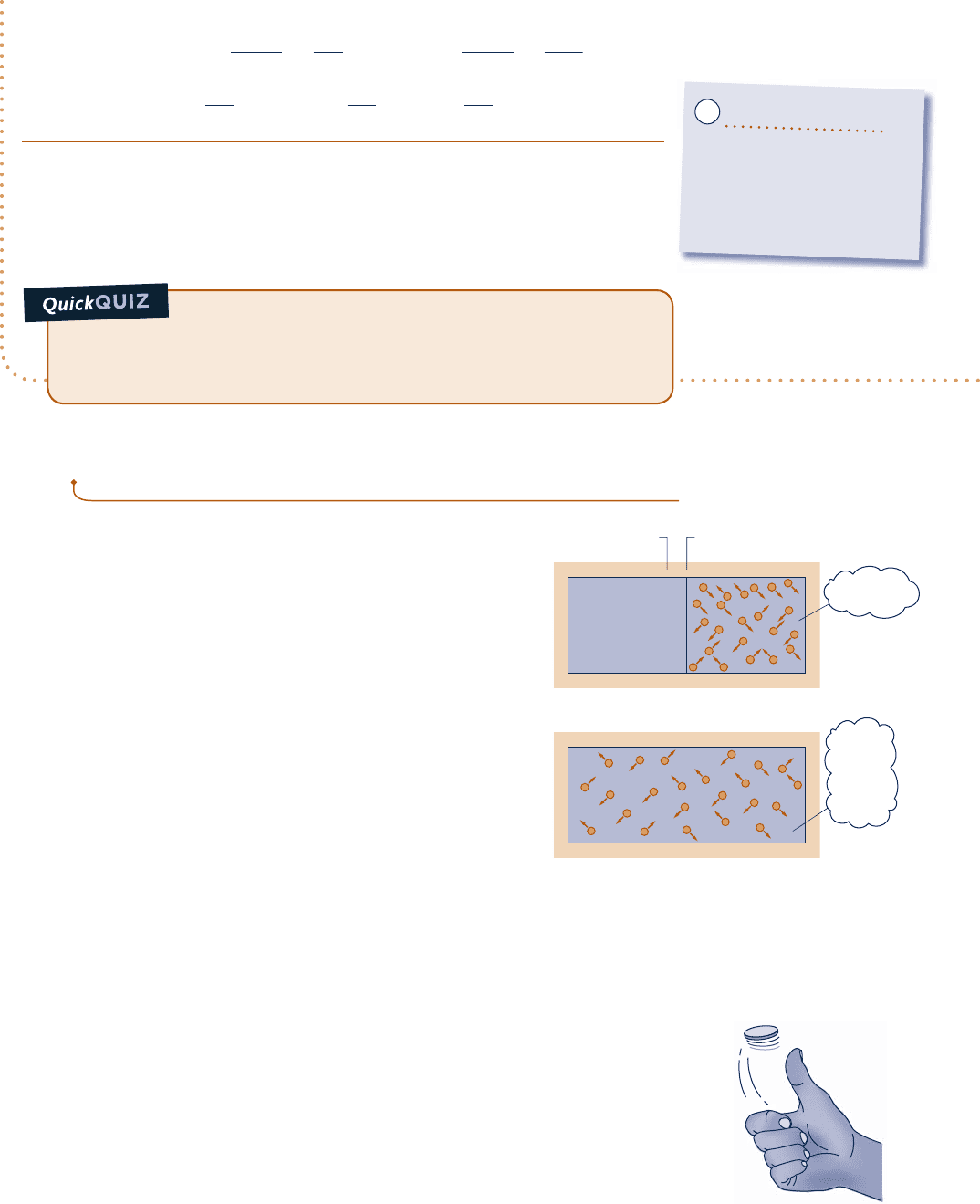
Consider N molecules initially contained in one half of the box
shown in Fig. 6.7a. The entire box is considered an isolated system.
We assume that the ideal gas model applies. In the initial condition,
the gas appears to be at equilibrium in terms of temperature, pressure,
and other properties. But, on the microscopic level the molecules are moving about
randomly. We do know for sure, though, that initially all molecules are on the right
side of the vessel.
Suppose we remove the partition and wait until equilibrium is reached again, as
in Fig. 6.7b. Because the system is isolated, the internal energy U does not change:
U
2
5 U
1
. Further, because the internal energy of an ideal gas depends on temperature
alone, the temperature is unchanged: T
2
5 T
1
. Still, at the final state a given molecule
has twice the volume in which to move: V
2
5 2V
1
. Just like a coin toss, the probability
that the molecule is on one side or the other is now ½, which is the same as the
volume ratio V
1
/V
2
. In the final condition, we have less knowledge about where each
molecule is than we did originally.
We can evaluate the change in entropy for the process of Fig. 6.7 by applying
Eq. 6.17, expressed in terms of volumes and on a molar basis. The entropy change for
If the mass of the metal bar were 0.45 lb, determine the final
equilibrium temperature, in 8R, and the amount of entropy produced, in
Btu/8R, keeping all other given data the same. Ans. 5338R, 0.0557
Btu/8R.
Inserting values
s 5 120 lb2a1.0
Btu
lb ? 8R
b ln
535
530
1 10.8 lb2a0.1
Btu
lb ? 8R
b ln
535
1900
➊➋
5 a0.1878
Btu
8R
b1 a20.1014
Btu
8R
b5 0.0864
Btu
8R
➊
The metal bar experiences a decrease in entropy. The entropy of the water
increases. In accord with the increase of entropy principle, the entropy of the
isolated system increases.
➋
The value of
s
is sensitive to roundoff in the value of T
f.
Ability to…
❑
apply the closed system
energy and entropy balances.
❑
apply the incompressible
substance model.
✓
Skills Developed
6.8 Directionality of Processes 305
Fig. 6.7
N molecules a box.
(a)
(b)
U
1
, T
1
, V
1
, S
1
Insulation Partition
Initially
Evacuated
U
2
= U
1
T
2
= T
1
V
2
= 2V
1
S
2
> S
1
c06UsingEntropy.indd Page 305 7/1/10 8:54:09 AM user-s146c06UsingEntropy.indd Page 305 7/1/10 8:54:09 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

306 Chapter 6
Using Entropy
the constant-temperature process is
1S
2
2 S
1
2
/
n 5 R ln1V
2
/
V
1
2 (6.31)
where n is the amount of substance on a molar basis (Eq. 1.8). Next, we consider how
the entropy change would be evaluated from a microscopic point of view.
Through more complete molecular modeling and statistical analysis, the total num-
ber of positions and velocities 2 microstates 2 available to a single molecule can be
calculated. This total is called the thermodynamic probability, w. For a system of N
molecules, the thermodynamic probability is w
N
. In statistical thermodynamics, entropy
is considered to be proportional to ln(w)
N
. That is, S ~ N ln(w). This gives the
Boltzmann relation
S
/
N 5 k ln w (6.32)
where the proportionality factor, k, is called Boltzmann’s constant.
Applying Eq. 6.32 to the process of Fig. 6.7, we get
1
S
2
2 S
1
2
/
N 5 k ln
1
w
2
2
2 k ln
1
w
1
2
5 k ln
1
w
2
/
w
1
2
(6.33)
Comparing Eqs. 6.31 and 6.33, the expressions for entropy change coincide when
k 5 nR
/
N
and w
2
/w
1
5 V
2
/V
1
. The first of these expressions allows Boltzmann’s constant
to be evaluated, giving k 5 1.3806 3 10
223
J/K. Also, since V
2
. V
1
and w
2
. w
1
, Eqs. 6.31
and 6.33 each predict an increase of entropy owing to entropy production during the
irreversible adiabatic expansion in this example.
From Eq. 6.33, we see that any process that increases the number of possible
microstates of a system increases its entropy and conversely. Hence, for an isolated
system, processes occur only in such a direction that the number of microstates avail-
able to the system increases, resulting in our having less knowledge about the condi-
tion of individual particles. Because of this concept of decreased knowledge, entropy
reflects the microscopic disorder of the system. We can then say that the only pro-
cesses an isolated system can undergo are those that increase the disorder of the
system. This interpretation is consistent with the idea of directionality of processes
discussed previously.
The notion of entropy as a measure of disorder is sometimes used in fields other
than thermodynamics. The concept is employed in information theory, statistics, biol-
ogy, and even in some economic and social modeling. In these applications, the term
entropy is used as a measure of disorder without the physical aspects of the thought
experiment used here necessarily being implied.
Some 135 years ago, renowned nineteenth-century
physicist J. C. Maxwell wrote, “. . . the second law is
. . . a statistical . . . truth, for it depends on the fact that
the bodies we deal with consist of millions of molecules . . . [Still]
the second law is continually being violated . . . in any suffi-
ciently small group of molecules belonging to a real body.”
Although Maxwell’s view was bolstered by theorists over the
years, experimental confirmation proved elusive. Then, in 2002,
experimenters reported they had demonstrated violations of the
second law: at the micron scale over time intervals of up to 2
seconds, entropy was consumed, not produced [see Phys. Rev.
Lett. 89, 050601 (2002)].
While few were surprised that experimental confirmation had
at last been achieved, some were surprised by implications of
the research for the twenty-first-century field of nanotechnology:
The experimental results suggest inherent limitations on nano-
machines. These tiny devices—only a few molecules in size—may
not behave simply as miniaturized versions of their larger coun-
terparts; and the smaller the device, the more likely its motion
and operation could be disrupted unpredictably. Occasionally
and uncontrollably, nanomachines may not perform as designed,
perhaps even capriciously running backward. Still, designers of
these machines will applaud the experimental results if they lead
to deeper understanding of behavior at the nanoscale.
“Breaking” the Second Law Has Implications for Nanotechnology
microstates
thermodynamic probability
Boltzmann relation
disorder
c06UsingEntropy.indd Page 306 5/26/10 2:41:03 PM user-s146c06UsingEntropy.indd Page 306 5/26/10 2:41:03 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
BIOCONNECTIONS Do living things violate the second law of thermody-
namics because they seem to create order from disorder? Living things are not iso-
lated systems as considered in the previous discussion of entropy and disorder.
Living things interact with their surroundings and are influenced by their surroundings. For
instance, plants grow into highly ordered cellular structures synthesized from atoms and
molecules originating in the earth and its atmosphere. Through interactions with their sur-
roundings, plants exist in highly organized states and are able to produce within them-
selves even more organized, lower entropy states. In keeping with the second law, states
of lower entropy can be realized within a system as long as the total entropy of the system
and its surroundings increases. The self-organizing tendency of living things is widely
observed and fully in accord with the second law.
6.9 Entropy Rate Balance for Control
Volumes
Thus far the discussion of the entropy balance concept has been restricted to the case
of closed systems. In the present section the entropy balance is extended to control
volumes.
Like mass and energy, entropy is an extensive property, so it too can be transferred
into or out of a control volume by streams of matter. Since this is the principal dif-
ference between the closed system and control volume forms, the control volume
entropy rate balance
can be obtained by modifying Eq. 6.28 to account for these
entropy transfers. The result is
d
S
cv
dt
5
a
j
Q
#
j
T
j
1
a
i
m
#
i
s
i
2
a
e
m
#
e
s
e
1 s
#
cv
(6.34)
rate of rates of rate of
entropy entropy entropy
change transfer production
where dS
cv
/dt represents the time rate of change of entropy within the control volume.
The terms m
#
i
s
i
and m
#
e
s
e
account, respectively, for rates of entropy transfer accompany-
ing mass flow
into and out of the control volume. The term Q
#
j
represents the time
rate of heat transfer at the location on the boundary where the instantaneous tem-
perature is T
j
. The ratio Q
#
j
/
T
j
accounts for the accompanying rate of entropy transfer.
The term s
#
cv
denotes the time rate of entropy production due to irreversibilities
within the control volume.
Integral Form of the Entropy Rate Balance
As for the cases of the control volume mass and energy rate balances, the entropy
rate balance can be expressed in terms of local properties to obtain forms that are
more generally applicable. Thus, the term S
cv
(t), representing the total entropy associ-
ated with the control volume at time t, can be written as a volume integral
S
cv
1t25
#
V
rs d
V
where r and s denote, respectively, the local density and specific entropy. The rate of
entropy transfer accompanying heat transfer can be expressed more generally as an
integral over the surface of the control volume
£
time rate of entropy
transfer accompanying
heat transfer
§
5
#
A
a
q
#
T
b
b
dA
control volume entropy
rate balance
entropy transfer
accompanying mass flow
6.9 Entropy Rate Balance for Control Volumes 307
A
A
Entropy_Rate_Bal_CV
A.25 – Tabs a & b
c06UsingEntropy.indd Page 307 6/30/10 9:45:36 AM user-s146c06UsingEntropy.indd Page 307 6/30/10 9:45:36 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
308 Chapter 6 Using Entropy
where q
#
is the heat flux, the time rate of heat transfer per unit of surface area, through
the location on the boundary where the instantaneous temperature is T. The subscript
“b” is added as a reminder that the integrand is evaluated on the boundary of the
control volume. In addition, the terms accounting for entropy transfer accompanying
mass flow can be expressed as integrals over the inlet and exit flow areas, resulting
in the following form of the entropy rate balance
d
dt
#
V
rs dV 5
#
A
a
q
#
T
b
b
dA 1
a
i
a
#
A
srV
n
dA
b
i
2
a
e
a
#
A
srV
n
dA
b
e
1 s
#
cv
(6.35)
where V
n
denotes the normal component in the direction of flow of the velocity
relative to the flow area. In some cases, it is also convenient to express the entropy
production rate as a volume integral of the local volumetric rate of entropy produc-
tion within the control volume. The study of Eq. 6.35 brings out the assumptions
underlying Eq. 6.34. Finally, note that for a closed system the sums accounting for
entropy transfer at inlets and exits drop out, and Eq. 6.35 reduces to give a more
general form of Eq. 6.28.
6.10 Rate Balances for Control Volumes
at Steady State
Since a great many engineering analyses involve control volumes at steady state, it is
instructive to list steady-state forms of the balances developed for mass, energy, and
entropy. At steady state, the conservation of mass principle takes the form
a
i
m
#
i
5
a
e
m
#
e
(4.6)
The energy rate balance at steady state is
0 5 Q
#
cv
2 W
#
cv
1
a
i
m
#
i
ah
i
1
V
2
i
2
1 gz
i
b2
a
e
m
#
e
ah
e
1
V
2
e
2
1 gz
e
b
(4.18)
Finally, the steady-state form of the entropy rate balance is obtained by reducing
Eq. 6.34 to give
0 5
a
j
Q
#
j
T
j
1
a
i
m
#
i
s
i
2
a
e
m
#
e
s
e
1 s
#
cv
(6.36)
These equations often must be solved simultaneously, together with appropriate prop-
erty relations.
Mass and energy are conserved quantities, but entropy is not conserved. Equation 4.6
indicates that at steady state the total rate of mass flow into the control volume equals
the total rate of mass flow out of the control volume. Similarly, Eq. 4.18 indicates
that the total rate of energy transfer into the control volume equals the total rate of
energy transfer out of the control volume. However, Eq. 6.36 requires that the rate
at which entropy is transferred out must exceed the rate at which entropy enters, the
difference being the rate of entropy production within the control volume owing to
irreversibilities.
6.10.1
One-Inlet, One-Exit Control Volumes at Steady State
Since many applications involve one-inlet, one-exit control volumes at steady state, let
us also list the form of the entropy rate balance for this important case. Thus, Eq. 6.36
reduces to read
steady-state entropy
rate balance
c06UsingEntropy.indd Page 308 5/26/10 2:41:05 PM user-s146c06UsingEntropy.indd Page 308 5/26/10 2:41:05 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

0 5
a
j
Q
#
j
T
j
1 m
#
1s
1
2 s
2
21 s
#
cv
(6.37)
Or, on dividing by the mass flow rate m
#
and rearranging
s
2
2 s
1
5
1
m
#
a
a
j
Q
#
j
T
j
b1
s
#
cv
m
#
(6.38)
The two terms on the right side of Eq. 6.38 denote, respectively, the rate of entropy
transfer accompanying heat transfer and the rate of entropy production within the
control volume, each per unit of mass flowing through the control volume. From Eq. 6.38
it can be concluded that the entropy of a unit of mass passing from inlet to exit can
increase, decrease, or remain the same. Furthermore, because the value of the second
term on the right can never be negative, a decrease in the specific entropy from inlet
to exit can be realized only when more entropy is transferred out of the control
volume accompanying heat transfer than is produced by irreversibilities within the
control volume. When the value of this entropy transfer term is positive, the specific
entropy at the exit is greater than the specific entropy at the inlet whether internal
irreversibilities are present or not. In the special case where there is no entropy
transfer accompanying heat transfer, Eq. 6.38 reduces to
s
2
2 s
1
5
s
#
cv
m
#
(6.39)
Accordingly, when irreversibilities are present within the control volume, the entropy
of a unit of mass increases as it passes from inlet to exit. In the limiting case in which
no irreversibilities are present, the unit mass passes through the control volume with
no change in its entropy—that is, isentropically.
6.10.2
Applications of the Rate Balances to Control Volumes
at Steady State
The following examples illustrate the use of the mass, energy, and entropy balances
for the analysis of control volumes at steady state. Carefully note that property rela-
tions and property diagrams also play important roles in arriving at solutions.
In Example 6.6, we evaluate the rate of entropy production within a turbine oper-
ating at steady state when there is heat transfer from the turbine.
6.10 Rate Balances for Control Volumes at Steady State 309
Determining Entropy Production in a Steam Turbine
c c c c EXAMPLE 6.6 c
Steam enters a turbine with a pressure of 30 bar, a temperature of 4008C, and a velocity of 160 m/s. Saturated
vapor at 1008C exits with a velocity of 100 m/s. At steady state, the turbine develops work equal to 540 kJ per kg
of steam flowing through the turbine. Heat transfer between the turbine and its surroundings occurs at an aver-
age outer surface temperature of 350 K. Determine the rate at which entropy is produced within the turbine per kg
of steam flowing, in kJ/kg
?
K. Neglect the change in potential energy between inlet and exit.
SOLUTION
Known:
Steam expands through a turbine at steady state for which data are provided.
Find: Determine the rate of entropy production per kg of steam flowing.
A
A
Entropy_Rate_Bal_CV
A.25 – Tab c
A
A
Turbine
A.19 – Tab d
c06UsingEntropy.indd Page 309 6/30/10 11:30:09 AM user-s146c06UsingEntropy.indd Page 309 6/30/10 11:30:09 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
310 Chapter 6 Using Entropy
Analysis: To determine the entropy production per unit mass flowing through the turbine, begin with mass and
entropy rate balances for the one-inlet, one-exit control volume at steady state:
m
#
1
5 m
#
2
0 5
a
j
Q
#
j
T
j
1 m
#
1
s
1
2 m
#
2
s
2
1 s
#
cv
Since heat transfer occurs only at T
b
5 350 K, the first term on the right side of the entropy rate balance reduces
to Q
#
cv
/
T
b
. Combining the mass and entropy rate balances
0 5
Q
#
cv
T
b
1 m
#
1s
1
2 s
2
21 s
#
cv
where m
#
is the mass flow rate. Solving for s
#
cv
/
m
#
s
#
cv
m
#
52
Q
#
cv
y
m
#
T
b
1 1s
2
2 s
1
2
The heat transfer rate, Q
#
cv
/
m
#
, required by this expression is evaluated next.
Reduction of the mass and energy rate balances results in
Q
#
cv
m
#
5
W
#
cv
m
#
1 1h
2
2 h
1
21 a
V
2
2
2 V
2
1
2
b
where the potential energy change from inlet to exit is dropped by assumption 3. From Table A-4 at 30 bar,
4008C, h
1
5 3230.9 kJ/kg, and from Table A-2, h
2
5 h
g
(1008C) 5 2676.1 kJ/kg. Thus
Q
#
cv
m
#
5 540
kJ
kg
1 12676.1 2 3230.92a
kJ
kg
b1 c
11002
2
2 11602
2
2
da
m
2
s
2
b`
1 N
1 kg ? m
/
s
2
``
1 kJ
10
3
N ? m
`
5 540 2 554.8 2 7.8 5222.6 kJ
/
k
g
From Table A-2, s
2
5 7.3549 kJ/kg
?
K, and from Table A-4, s
1
5 6.9212 kJ/
kg
?
K. Inserting values into the expression for entropy production
s
#
cv
m
#
52
1
222.6 kJ
/
kg
2
350 K
1 17.3549 2 6.92122
a
kJ
kg ? K
b
5 0.0646 1 0.4337 5 0.498 kJ
/
k
g
? K
If the boundary were located to include the turbine and a por-
tion of the immediate surroundings so heat transfer occurs at the tem-
perature of the surroundings, 293 K, determine the rate at which entropy
is produced within the enlarged control volume, in kJ/K per kg of steam
flowing, keeping all other given data the same. Ans. 0.511 kJ/kg
?
K.
Ability to…
❑
apply the control volume
mass, energy and entropy
rate balances.
❑
retrieve property data for
water.
✓
Skills Developed
Engineering Model:
1.
The control volume shown
on the accompanying
sketch is at steady state.
2. Heat transfer from the
turbine to the surroundings
occurs at a specified average
outer surface temperature.
3. The change in potential
energy between inlet and
exit can be neglected.
1
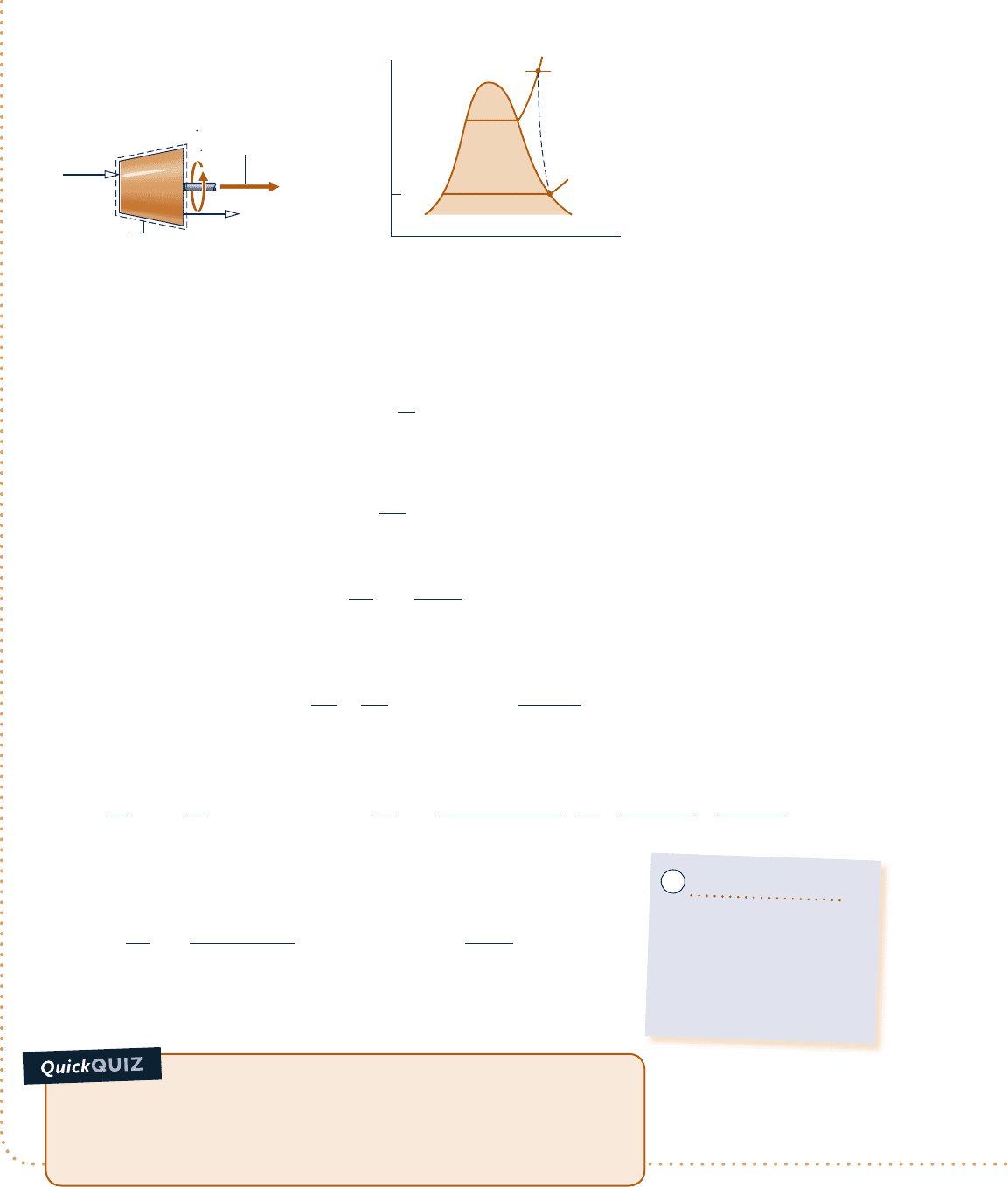
2
p
1
T
1
V
1
= 30 bar
= 400°C
= 160 m/s
Surroundings
at 293 K
T
2
= 100°C
Saturated vapor
V
2
= 100 m/s
W
cv
–––
m
= 540 kJ/kg
T
b
= 350 K
1
2
400°C
30 bar
T
100°C
s
Fig. E6.6
Schematic and Given Data:
c06UsingEntropy.indd Page 310 5/26/10 2:41:06 PM user-s146c06UsingEntropy.indd Page 310 5/26/10 2:41:06 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
In Example 6.7, the mass, energy, and entropy rate balances are used to evaluate
a performance claim for a device producing hot and cold streams of air from a single
stream of air at an intermediate temperature.
6.10 Rate Balances for Control Volumes at Steady State 311
Evaluating a Performance Claim
c c c c EXAMPLE 6.7 c
An inventor claims to have developed a device requiring no energy transfer by work, W
#
cv
, or heat transfer, yet able
to produce hot and cold streams of air from a single stream of air at an intermediate temperature. The inventor
provides steady-state test data indicating that when air enters at a temperature of 708F and a pressure of 5.1 atm,
separate streams of air exit at temperatures of 0 and 1758F, respectively, and each at a pressure of 1 atm. Sixty per-
cent of the mass entering the device exits at the lower temperature. Evaluate the inventor’s claim, employing the
ideal gas model for air and ignoring changes in the kinetic and potential energies of the streams from inlet to exit.
SOLUTION
Known:
Data are provided for a device that at steady state produces hot and cold streams of air from a single
stream of air at an intermediate temperature without energy transfers by work or heat.
Find: Evaluate whether the device can operate as claimed.
Schematic and Given Data:
T
1
= 70°F
p
1
= 5.1 atm
T
3
= 0°F
p
3
= 1 atm
T
2
= 175°F
p
2
= 1 atm
1
3
2
Inlet
Cold outlet
Hot outlet
Fig. E6.7
Analysis: For the device to operate as claimed, the conservation of mass and energy principles must be satisfied.
The second law of thermodynamics also must be satisfied; and in particular the rate of entropy production cannot
be negative. Accordingly, the mass, energy and entropy rate balances are considered in turn.
With assumptions 1–3, the mass and energy rate balances reduce, respectively, to
m
#
1
5 m
#
2
1 m
#
3
0 5 m
#
1
h
1
2 m
#
2
h
2
2 m
#
3
h
3
Since m
#
3
5 0.6m
#
1
, it follows from the mass rate balance that m
#
3
5 0.4m
#
1
. By combining the mass and energy
rate balances and evaluating changes in specific enthalpy using constant c
p
, the energy rate balance is also satis-
fied. That is
0 5
1
m
#
2
1 m
#
3
2
h
1
2 m
#
2
h
2
2 m
#
3
h
3
5 m
#
2
1
h
1
2 h
2
2
1 m
#
3
1
h
1
2 h
3
2
5 0.4m
#
1
3
c
p
1
T
1
2 T
2
24
1 0.6m
#
1
3
c
p
1
T
1
2 T
3
24
5 0.4
1
T
1
2 T
2
2
1 0.6
1
T
1
2 T
3
2
5 0.4
1
2105
2
1 0.6
1
70
2
5
0
➋
Engineering Model:
1.
The control volume shown on the
accompanying sketch is at steady state.
2. For the control volume, W
#
cv
5 0 and Q
#
cv
5 0.
3. Changes in the kinetic and potential
energies from inlet to exit can be ignored.
4. The air is modeled as an ideal gas with
constant c
p
5 0.24 Btu/lb
?
8R.
➊
A
A
Heat_Exchanger
A.22 – Tab d
c06UsingEntropy.indd Page 311 6/30/10 11:24:49 AM user-s146c06UsingEntropy.indd Page 311 6/30/10 11:24:49 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

312 Chapter 6 Using Entropy
Accordingly, with the given data the conservation of mass and energy principles are satisfied.
Since no significant heat transfer occurs, the entropy rate balance at steady state reads
0 5
a
j
Q
#
j
T
j
0
1 m
#
1
s
1
2 m
#
2
s
2
2 m
#
3
s
3
1 s
#
cv
Combining the mass and entropy rate balances
0 5
1
m
#
2
1 m
#
3
2
s
1
2 m
#
2
s
2
2 m
#
3
s
3
1 s
#
cv
5 m
#
2
1
s
1
2 s
2
2
1 m
#
3
1
s
1
2 s
3
2
1 s
#
cv
5 0.4m
#
1
1
s
1
2 s
2
2
1 0.6m
#
1
1
s
1
2 s
3
2
1 s
#
cv
Solving for s
#
cv
/
m
#
1
and using Eq. 6.22 to evaluate changes in specific entropy
s
#
cv
m
#
1
5 0.4 cc
p
ln
T
2
T
1
2 R ln
p
2
p
1
d1 0.6 cc
p
ln
T
3
T
1
2 R ln
p
3
p
1
d
5 0.4
ca
0.24
Btu
lb ? 8R
b
ln
635
530
2
a
1.986
28.97
Btu
lb ? 8R
b
ln
1
5.1
d
1 0.6
ca
0.24
Btu
lb ? 8R
b
ln
460
530
2
a
1.986
28.97
Btu
lb ? 8R
b
ln
1
5.1
d
5 0.1086
B
tu
lb ? 8R
Thus, the second law of thermodynamics is also satisfied.
➎ On the basis of this evaluation, the inventor’s claim does not violate principles of thermodynamics.
➊ Since the specific heat c
p
of air varies little over the temperature interval from 0 to 1758F, c
p
can be taken as
constant. From Table A-20E, c
p
5 0.24 Btu/lb
?
8R.
➋ Since temperature differences are involved in this calculation, the temperatures can be either in 8R or 8F.
➌ In this calculation involving temperature ratios, the temperatures are in 8R.
Temperatures in 8F should not be used.
➍ If the value of the rate of entropy production had been negative or zero, the
claim would be rejected. A negative value is impossible by the second law and
a zero value would indicate operation without irreversibilities.
➎ Such devices do exist. They are known as vortex tubes and are used in indus-
try for spot cooling.
If the inventor would claim that the hot and cold streams exit
the device at 5.1 atm, evaluate the revised claim, keeping all other given
data the same. Ans. Claim invalid.
Ability to…
❑
apply the control volume
mass, energy and entropy
rate balances.
❑
apply the ideal gas model
with constant c
p
.
✓
Skills Developed
➌
➍
In Example 6.8, we evaluate and compare the rates of entropy production for
three components of a heat pump system. Heat pumps are considered in detail in
Chap. 10.
A
A
Compressor
A.20 – Tab d
Throttling_Dev
A.23 – Tab d
c06UsingEntropy.indd Page 312 6/30/10 11:24:23 AM user-s146c06UsingEntropy.indd Page 312 6/30/10 11:24:23 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
