Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

586 Chapter 12 Ideal Gas Mixture and Psychrometric Applications

EXAMPLE 12.8 Cooling Moist Air at Constant Volume

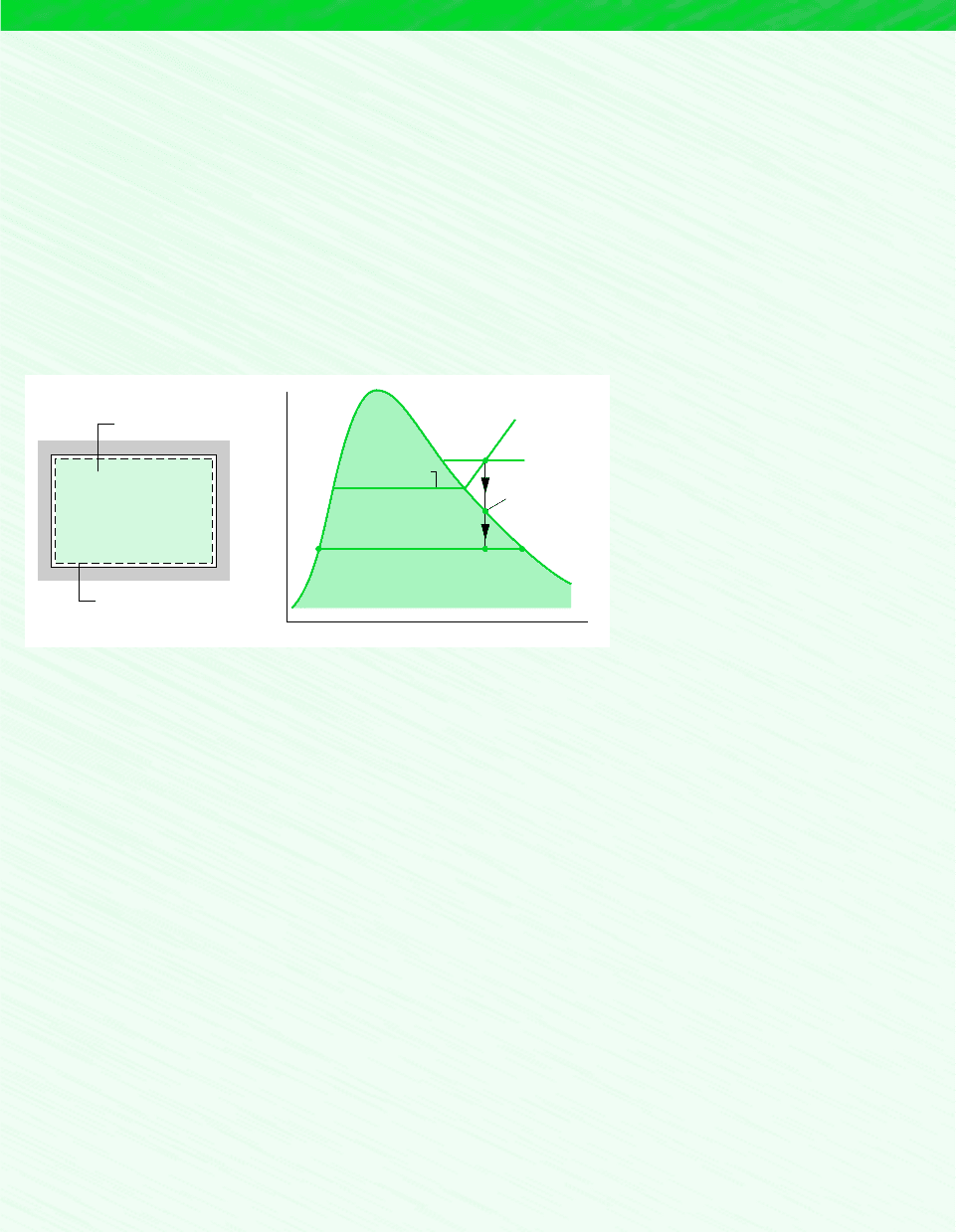
An air–water vapor mixture is contained in a rigid, closed vessel with a volume of 35 m

at 1.5 bar, 120C, and   10%.

The mixture is cooled at constant volume until its temperature is reduced to 22C. Determine (a) the dew point temperature

corresponding to the initial state, in C, (b) the temperature at which condensation actually begins, in C, and (c) the amount

of water condensed, in kg.

SOLUTION

Known: A rigid, closed tank with a volume of 35 m

containing moist air initially at 1.5 bar, 120C, and   10% is cooled

to 22C.

Find: Determine the dew point temperature at the initial state, in C, the temperature at which condensation actually begins,

in C, and the amount of water condensed, in kg.

Schematic and Given Data:

f2 g2

1′

Condensation

begins

Dew point

temperature

V = 35 m

Boundary

Initially moist air

at 1.5 bar, 120°C

= 10%

 Figure E12.8

Assumptions:

1. The contents of the tank are taken as a closed system. The system volume remains constant.

2. The gas phase can be treated as an ideal gas mixture. Each mixture component acts as an ideal gas existing alone in the

volume occupied by the gas phase at the mixture temperature.

3. When a liquid water phase is present, the water vapor exists as a saturated vapor at the system temperature. The liquid is

a saturated liquid at the system temperature.

Analysis:

(a) The dew point temperature at the initial state is the saturation temperature corresponding to the partial pressure p

. With

the given relative humidity and the saturation pressure at 120C from Table A-2

Interpolating in Table A-2 gives the dew point temperature as 60C, which is the temperature condensation would begin if the

moist air were cooled at constant pressure.

(b) Whether the water exists as a vapor only, or as liquid and vapor, it occupies the full volume, which remains constant. Ac-

cordingly, since the total mass of the water present is also constant, the water undergoes the constant specific volume process

illustrated on the accompanying T–v diagram. In the process from state 1 to state 1, the water exists as a vapor only. For the

process from state 1 to state 2, the water exists as a two-phase liquid–vapor mixture. Note that pressure does not remain con-

stant during the cooling process from state 1 to state 2.

State 1 on the T–v diagram denotes the state where the water vapor first becomes saturated. The saturation temperature

at this state is denoted as T . Cooling to a temperature less than T  would result in condensation of some of the water vapor

present. Since state 1 is a saturated vapor state, the temperature T  can be found by interpolating in Table A-2 with the specific

 f

 10.102 11.9852 0.1985 bar

12.5 Introducing Psychrometric Principles 587

volume of the water at this state. The specific volume of the vapor at state 1 equals the specific volume of the vapor at state 1,

which can be evaluated from the ideal gas equation

Interpolation in Table A-2 with v

 v

gives T  56C. This is the temperature at which condensation begins.

(c) The amount of condensate equals the difference between the initial and final amounts of water vapor present. The mass

of the water vapor present initially is

The mass of water vapor present finally can be determined from the quality. At the final state, the water forms a two-phase

liquid–vapor mixture having a specific volume of 9.145 m

/kg. Using this specific volume value, the quality x

of the

liquid–vapor mixture can be found as

where v

and v

are the saturated liquid and saturated vapor specific volumes at T

 22C, respectively.

Using the quality together with the known total amount of water present, 3.827 kg, the mass of the water vapor contained

in the system at the final state is

The mass of the condensate, m

, is then

When a moist air mixture is cooled at constant mixture volume, the temperature at which condensation begins is not the

dew point temperature corresponding to the initial state. In this case, condensation begins at 56C, but the dew point tem-

perature at the initial state, determined in part (a), is 60C.

 m

 m

 3.827  0.681  3.146 kg

 10.1782 13.8272 0.681 kg



 v



9.145  1.0022  10

3

51.447  1.0022  10

3

 0.178



35 m

9.145 m

/kg

 3.827 kg

 9.145





 a

8314

b a

393 K

0.1985  10

N/m

No additional fundamental concepts are required for the study of closed systems involv-

ing mixtures of dry air and water vapor. Example 12.9, which builds on Example 12.8, brings

out some special features of the use of conservation of mass and conservation of energy in

analyzing this kind of system. Similar considerations can be used to study other closed systems

involving moist air.

EXAMPLE 12.9 Evaluating Heat Transfer for Moist Air Cooling at Constant Volume

An air–water vapor mixture is contained in a rigid, closed vessel with a volume of 35 m

at 1.5 bar, 120C, and   10%.

The mixture is cooled until its temperature is reduced to 22C. Determine the heat transfer during the process, in kJ.

SOLUTION

Known: A rigid, closed tank with a volume of 35 m

containing moist air initially at 1.5 bar, 120C, and   10% is cooled

to 22C.

Find: Determine the heat transfer for the process, in kJ.

Schematic and Given Data: See the figure for Example 12.8.

❶

588 Chapter 12 Ideal Gas Mixture and Psychrometric Applications

Assumptions:

1. The contents of the tank are taken as a closed system. The system volume remains constant.

2. The gas phase can be treated as an ideal gas mixture. Each component acts as an ideal gas existing alone in the volume

occupied by the gas phase at the mixture temperature.

3. When a liquid water phase is present, the water vapor exists as a saturated vapor and the liquid is a saturated liquid, each

at the system temperature.

4. There is no work during the cooling process and no change in kinetic or potential energy.

Analysis: Reduction of the closed system energy balance using assumption 4 results in

where

and

In these equations, the subscripts a, v, and w denote, respectively, dry air, water vapor, and liquid water. The specific internal

energy of the water vapor at the initial state can be approximated as the saturated vapor value at T

. At the final state, the wa-

ter vapor is assumed to exist as a saturated vapor, so its specific internal energy is u

at T

. The liquid water at the final state

is saturated, so its specific internal energy is u

at T

Collecting the last three equations

The mass of dry air, m

, can be found using the ideal gas equation of state together with the partial pressure of the dry air

at the initial state obtained using p

 0.1985 bar from the solution to Example 12.8

Then, evaluating internal energies of dry air and water from Tables A-22 and A-2, respectively

The values for m

, m

, and m

are from the solution to Example 12.8.

The first underlined term in this equation for Q is evaluated with specific internal energies from the ideal gas table for air,

Table A-22. Steam table data are used to evaluate the second underlined term. The different datums for internal energy un-

derlying these tables cancel because each of these two terms involves internal energy differences. Since the specific heat

for dry air varies only slightly over the interval from 120 to 22C (Table A-20), the specific internal energy change of

the dry air could be evaluated alternatively using a constant c

value. This is left as an exercise.

2851.87  1638.28  290.44  9679.63 10,603 kJ

Q  40.389

1210.49  281.12 0.681 12405.72 3.146 192.322 3.827 12529.32

 40.389 kg







311.5  0.19852 10

N/m

4 135 m

18314



28.97 N

m/kg

K2 1393 K2

Q  m

 u

2 m

 m

 m

 m

 m

 m

 m

 m

 m

 m

 m

Q  U

 U

¢U  Q  W

 12.5.5 Evaluating Humidity Ratio Using the

Adiabatic-Saturation Temperature

The humidity ratio  of an air–water vapor mixture can be determined, in principle, knowing

the values of three mixture properties: the pressure p, the temperature T, and the adiabatic-

saturation temperature T

introduced in this section. The relationship among these quantities

adiabatic-saturation

temperature

❶

12.5 Introducing Psychrometric Principles 589

is obtained by applying conservation of mass and conservation of energy to an adiabatic sat-

uration process (see box).

Equations 12.48 and 12.49 give the humidity ratio  in terms of the adiabatic-saturation

temperature and other quantities:

(12.48)

where h

and h

denote the enthalpies of saturated liquid water and saturated water vapor, re-

spectively, obtained from the steam tables at the indicated temperatures. The enthalpies of

the dry air h

can be obtained from the ideal gas table for air. Alternatively, h

)  h

(T ) 

 T ), where c

is an appropriate constant value for the specific heat of dry air. The

humidity ratio  appearing in Eq. 12.48 is

(12.49)

where p

) is the saturation pressure at the adiabatic-saturation temperature and p is the

mixture pressure.

v¿  0.622

p  p

v 

2 h

1T 2 v¿ 3h

2 h

1T 2 h

MODELING AN ADIABATIC SATURATION PROCESS

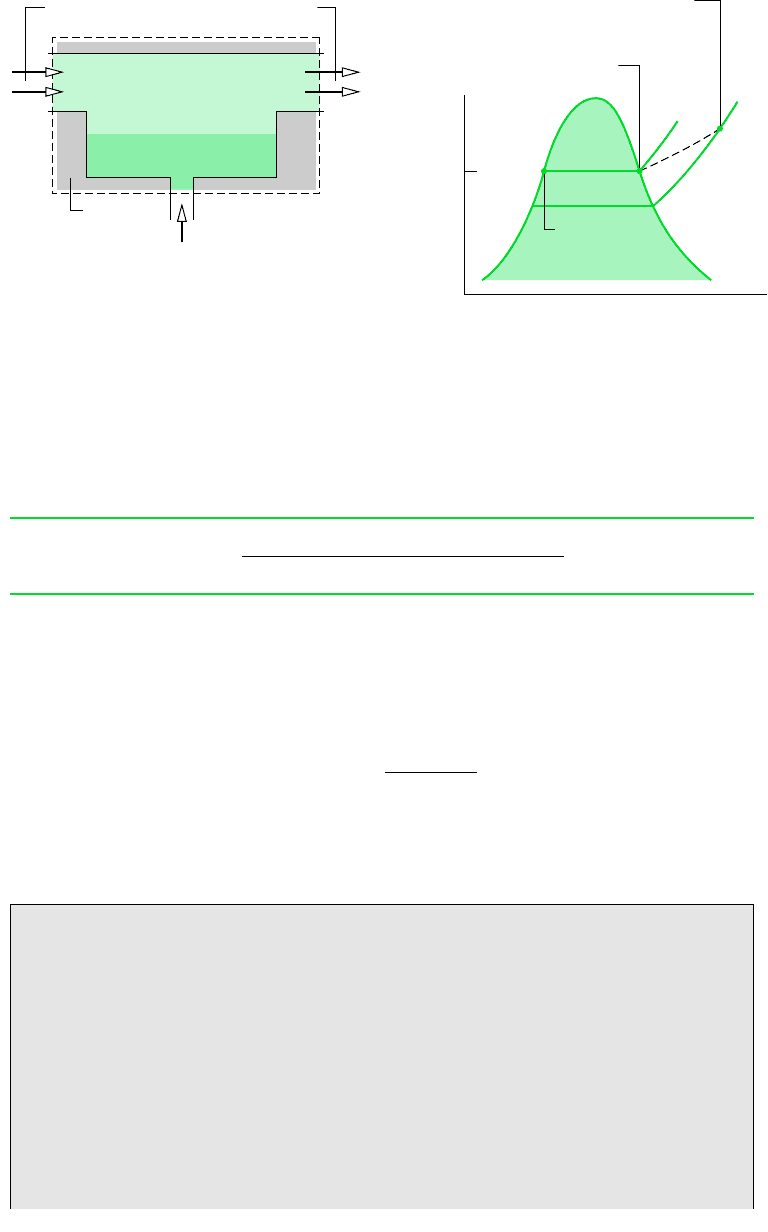
Figure 12.7 shows the schematic and process representations of an adiabatic saturator,

which is a two-inlet, single-exit device through which moist air passes. The device is

assumed to operate at steady state and without significant heat transfer with its sur-

roundings. An air–water vapor mixture of unknown humidity ratio  enters the adia-

batic saturator at a known pressure p and temperature T. As the mixture passes through

the device, it comes into contact with a pool of water. If the entering mixture is not

saturated (  100%), some of the water would evaporate. The energy required to

evaporate the water would come from the moist air, so the mixture temperature would

decrease as the air passes through the duct. For a sufficiently long duct, the mixture

would be saturated as it exits (  100%). Since a saturated mixture would be achieved

)

State of the water vapor

in the incoming moist air stream

State of the water

vapor in the

exiting moist air

stream

State of the

makeup water

Makeup water —

saturated liquid at T

mass flow rate = m

′

– m

Insulation

Moist air

p, T,

Saturated mixture

, ′, p

′

(a)(b)

 Figure 12.7

Adiabatic saturator. (a) Schematic. (b) Process representation.

590 Chapter 12 Ideal Gas Mixture and Psychrometric Applications

without heat transfer with the surroundings, the temperature of the exiting mixture is

the adiabatic-saturation temperature. As indicated on Fig. 12.7, a steady flow of

makeup water at temperature T

is added at the same rate at which water is evapo-

rated. The pressure of the mixture is assumed to remain constant as it passes through

the device. Equation 12.48 giving the humidity ratio  of the entering moist air in terms

of p, T, and T

can be obtained by applying conservation of mass and conservation of

energy to the adiabatic saturator, as follows.

At steady state, the mass flow rate of the dry air entering the device, , must equal

the mass flow rate of the dry air exiting. The mass flow rate of the makeup water is

the difference between the exiting and entering vapor flow rates denoted by and

respectively. These flow rates are labeled on Fig. 12.7a. At steady state, the energy rate

balance reduces to

Several assumptions underlie this expression: Each of the two moist air streams is mod-

eled as an ideal gas mixture of dry air and water vapor. Heat transfer with the sur-

roundings is assumed to be negligible. There is no work , and changes in kinetic

and potential energy are ignored.

Dividing by the mass flow rate of the dry air, , the energy rate balance can be

written on the basis of a unit mass of dry air passing through the device as

(12.50)

where and .

For the exiting saturated mixture, the partial pressure of the water vapor is the satu-

ration pressure corresponding to the adiabatic-saturation temperature, p

). Accord-

ingly, the humidity ratio ¿ can be evaluated knowing T

and the mixture pressure p,as

indicated by Eq. 12.49. In writing Eq. 12.50, the specific enthalpy of the entering water

vapor has been evaluated as that of saturated water vapor at the temperature of the

incoming mixture, in accordance with Eq. 12.47. Since the exiting mixture is saturated,

the enthalpy of the water vapor at the exit is given by the saturated vapor value at T

The enthalpy of the makeup water is evaluated as that of saturated liquid at T

When Eq. 12.50 is solved for , Eq. 12.48 results. The details of the solution are

left as an exercise. Although derived with reference to an adiabatic saturator, the rela-

tionship provided by Eq. 12.48 applies generally to moist air mixtures and is not re-

stricted to this type of system or even to control volumes. The relationship allows the

humidity ratio  to be determined for any moist air mixture for which the pressure p,

temperature T, and adiabatic-saturation temperature T

are known.

v¿  m



v  m



 vh

2moist air

entering

 31v¿  v2h

4makeup

water

 1h

 v¿h

2moist air

exiting

 m

2moist air

entering

 31m

 m

4makeup

water

 1m

 m

2moist air

exiting



12.6 Psychrometers: Measuring the Wet-Bulb

and Dry-Bulb Temperatures

For moist air mixtures in the normal pressure and temperature ranges of psychrometrics, the

readily-measured wet-bulb temperature is an important parameter.

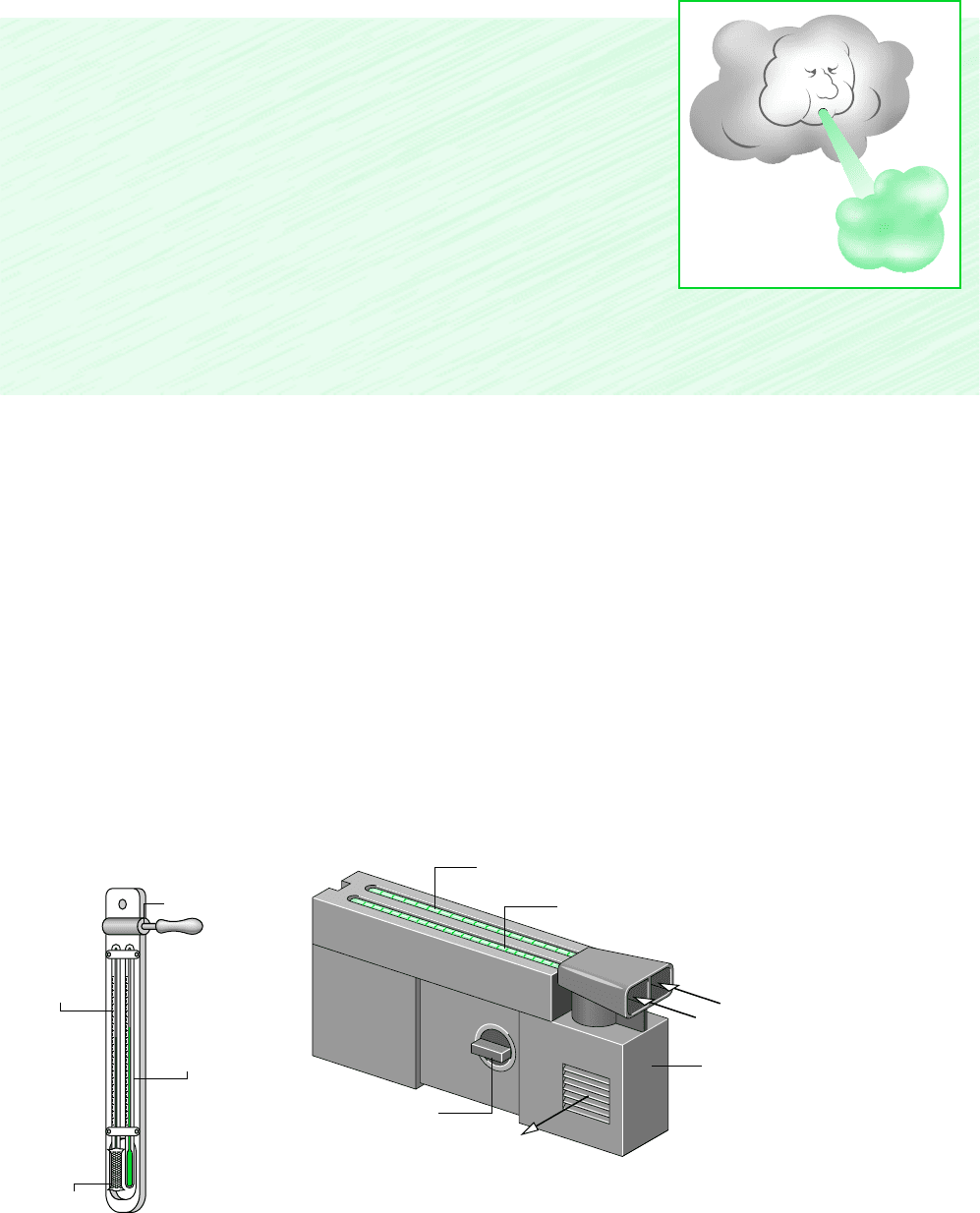
The wet-bulb temperature is read from a wet-bulb thermometer, which is an ordinary

liquid-in-glass thermometer whose bulb is enclosed by a wick moistened with water. The

term dry-bulb temperature refers simply to the temperature that would be measured by a

thermometer placed in the mixture. Often a wet-bulb thermometer is mounted together with

a dry-bulb thermometer to form an instrument called a psychrometer.

wet-bulb temperature

psychrometer

dry-bulb temperature

12.6 Psychrometers: Measuring the Wet-Bulb and Dry-Bulb Temperatures 591

The psychrometer of Fig. 12.8a is whirled in the air whose wet- and dry-bulb temperatures

are to be determined. This induces air flow over the two thermometers. For the psychrometer

of Fig. 12.8b, the air flow is induced by a battery-operated fan. In each type of psychrome-

ter, if the surrounding air is not saturated, water in the wick of the wet-bulb thermometer evap-

orates and the temperature of the remaining water falls below the dry-bulb temperature. Even-

tually a steady-state condition is attained by the wet-bulb thermometer. The wet- and dry-bulb

temperatures are then read from the respective thermometers. The wet-bulb temperature de-

pends on the rates of heat and mass transfer between the moistened wick and the air. Since

these depend in turn on the geometry of the thermometer, air velocity, supply water temper-

ature, and other factors, the wet-bulb temperature is not a mixture property.

For moist air mixtures in the normal pressure and temperature ranges of psychrometric ap-

plications, the adiabatic saturation temperature introduced in Sec. 12.5.5 is closely approximated

by the wet-bulb temperature. Accordingly, the humidity ratio for any such mixture can be

calculated by using the wet-bulb temperature in Eqs. 12.48 and 12.49 in place of the adiabatic-

saturation temperature. Close agreement between the adiabatic-saturation and wet-bulb temper-

atures is not generally found for moist air departing from normal psychrometric conditions.

Air in

Air out

Battery-

operated

fan

Dry-bulb

thermometer

Wet-bulb

thermometer

Switch

(b)

Bearing

Handle

Wet-bulb

thermometer

Dry-bulb

thermometer

Wick

(a)

 Figure 12.8

Psychrometers. (a) Sling psychrometer. (b) Aspirating psychrometer.

are better armed to

avoid exposure that

can lead to such seri-

ous medical problems

as frostbite.

The improved

measure was devel-

oped by universities,

international scientific

societies, and govern-

ment in a two-year

effort that led to the

new standard being

adopted in the United States and Canada. Further upgrades

are in the works to include the amount of cloud cover in the

formula, since solar radiation is also an important factor in

how cold it feels.

How Cold is Cold?

Thermodynamics in the News...

The National Weather Service is finding better ways to help

measure our misery during cold snaps so we can avoid

weather dangers. The wind chill index, for many years based

on a single 1945 study, was recently upgraded using new phys-

iological data and computer modeling to better reflect the

perils of cold winds and freezing temperatures.

The new wind chill index is a standardized “temperature”

that accounts for both the actual air temperature and the wind

speed. The formula on which it is based uses measurements of

skin tissue thermal resistance and computer models of the wind

patterns over the human face, together with principles of heat

transfer. Using the new index, an air temperature of 5F and a

wind speed of 25 miles per hour correspond to a wind chill tem-

perature of 40F. The old index assigned a wind chill of only

20F to the same conditions. With the new information, people

592 Chapter 12 Ideal Gas Mixture and Psychrometric Applications

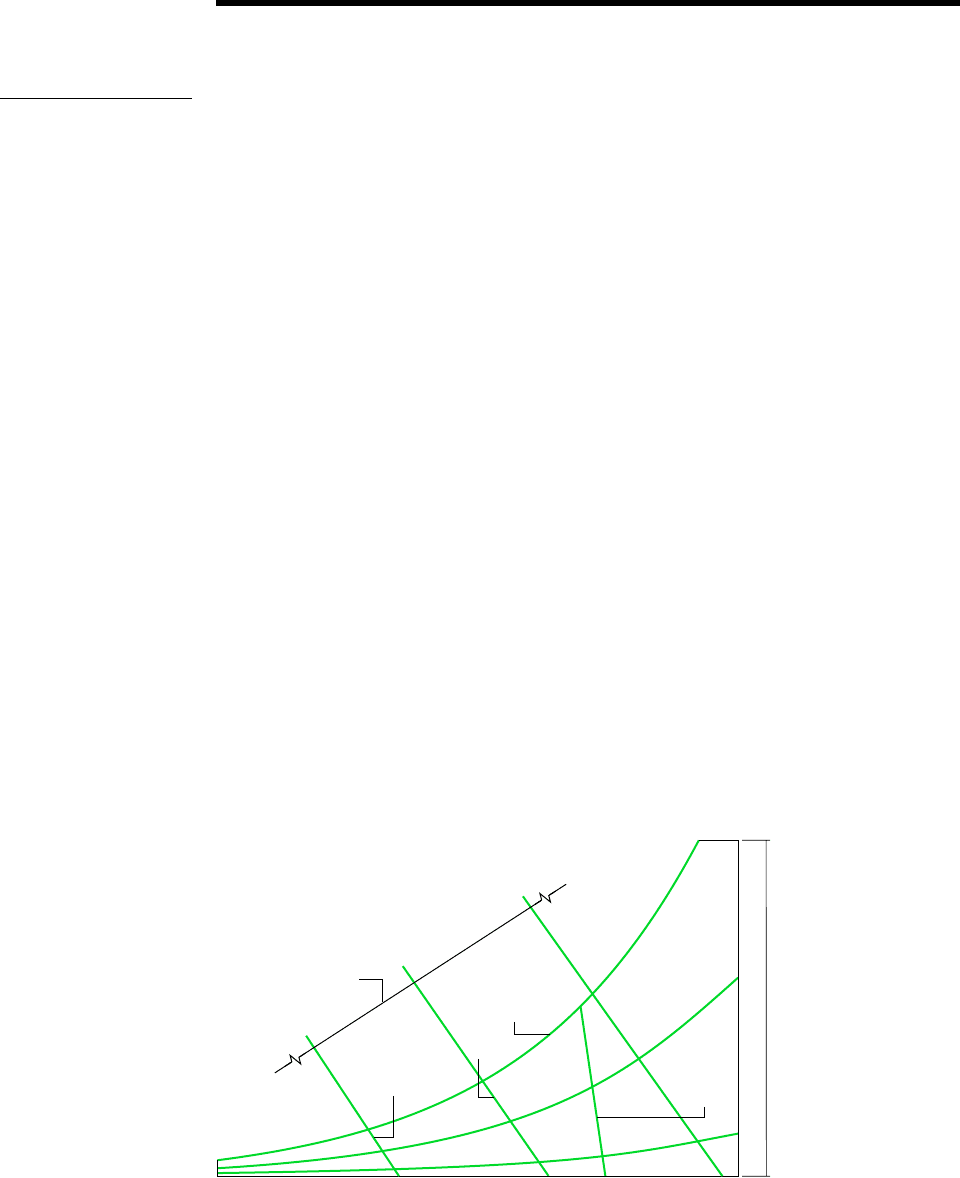
Graphical representations of several important properties of moist air are provided by

psychrometric charts. The main features of one form of chart are shown in Fig. 12.9. A

complete chart in SI units is given in Fig. A-9. This chart is constructed for a mixture

pressure of 1 atm, but charts for other mixture pressures are also available. When the mix-

ture pressure differs only slightly from 1 atm, Figs. A-9 remain sufficiently accurate for

engineering analyses. In this text, such differences are ignored.

Let us consider several features of the psychrometric chart:

 Referring to Fig. 12.9, note that the abscissa gives the dry-bulb temperature and the

ordinate provides the humidity ratio. For charts in SI, the temperature is in C and

 is expressed in kg, or g, of water vapor per kg of dry air.

 Equation 12.43 shows that for fixed mixture pressure there is a direct correspondence

between the partial pressure of the water vapor and the humidity ratio. Accordingly, the

vapor pressure also can be shown on the ordinate, as illustrated on Fig. 12.9.

 Curves of constant relative humidity are shown on psychrometric charts. On

Fig. 12.9, curves labeled   100, 50, and 10% are indicated. Since the dew point

is the state where the mixture becomes saturated when cooled at constant vapor

pressure, the dew point temperature corresponding to a given moist air state can be

determined by following a line of constant  (constant p

) to the saturation line,

  100%. The dew point temperature and dry-bulb temperature are identical for

states on the saturation curve.

 Psychrometric charts also give values of the mixture enthalpy per unit mass of dry air

in the mixture: h

 h

. In Fig. A-9, the mixture enthalpy has units of kJ per kg of

dry air. The numerical values provided on these charts are determined relative to the

following special reference states and reference values. In Fig. A-9, the enthalpy of the

dry air h

is determined relative to a zero value at 0C, and not 0 K as in Table A-22.

Accordingly, in place of Eq. 3.49 used to develop the enthalpy data of Tables A-22,

the following expression is employed to evaluate the enthalpy of the dry air for use



12.7 Psychrometric Charts

psychrometric chart

= 100%

= 50%

= 10%

Volume

per unit

mass of

dry air

Wet-bulb and

dew point

temperature

scales

Scale for the

mixture enthalpy

per unit mass of

dry air

Barometric pressure = 1 atm

Dry-bulb temperature

 Figure 12.9 Psychrometric chart.

12.8 Analyzing Air-Conditioning Processes 593

on the psychrometric chart:

(12.51)

where c

is a constant value for the specific heat c

of dry air and T(C) denotes

the temperature in C. In the temperature range of Fig. A-9, c

can be taken as

1.005 kJ/kg · K. On Figs. A-9 the enthalpy of the water vapor h

is evaluated as h

the dry-bulb temperature of the mixture from Table A-2.

 Another important parameter on psychrometer charts is the wet-bulb temperature. As

illustrated by Figs. A-9, constant T

lines run from the upper left to the lower right of

the chart. The relationship between the wet-bulb temperature and other chart quantities

is provided by Eq. 12.48. The wet-bulb temperature can be used in this equation in

place of the adiabatic-saturation temperature for the states of moist air located on

Figs. A-9.

 Lines of constant wet-bulb temperature are approximately lines of constant mixture

enthalpy per unit mass of dry air. This feature can be brought out by study of the

energy balance for the adiabatic saturator, Eq. 12.50. Since the contribution of the

energy entering the adiabatic saturator with the makeup water is normally much

smaller than that of the moist air, the enthalpy of the entering moist air is very

nearly equal to the enthalpy of the saturated mixture exiting. Accordingly, all states

with the same value of the wet-bulb temperature (adiabatic-saturation temperature)

have nearly the same value for the mixture enthalpy per unit mass of dry air. Al-

though Figs. A-9 ignore this slight effect, some psychrometric charts are drawn to

show the departure of lines of constant wet-bulb temperature from lines of constant

mixture enthalpy.

 As shown on Fig. 12.9, psychrometric charts also provide lines representing volume per

unit mass of dry air, Vm

. Figure A-9 gives this quantity in units of m

/kg. These spe-

cific volume lines can be interpreted as giving the volume of dry air or of water vapor,

per unit mass of dry air, since each mixture component is considered to fill the entire

volume.

The psychrometric chart is easily used.  for example. . . a psychrometer indicates

that in a classroom the dry-bulb temperature is 20C and the wet-bulb temperature is 15C.

Locating the mixture state on Fig. A-9 corresponding to the intersection of these tempera-

tures, we read   0.0086 kg(vapor)/kg(dry air) and   60%. 





273.15 K

dT  c

T 1°C2



12.8 Analyzing Air-Conditioning Processes

The purpose of the present section is to study typical air-conditioning processes using

the psychrometric principles developed in this chapter. Specific illustrations are pro-

vided in the form of solved examples involving control volumes at steady state. In

each case, the methodology introduced in Sec. 12.8.1 is employed to arrive at the solu-

tion. To reinforce the psychrometric principles developed in the present chapter, the re-

quired psychrometric parameters are determined in most cases using tabular data provided

in the appendix. It is left as an exercise to check these values by means of a psychro-

metric chart.

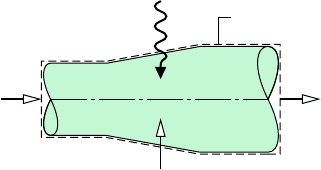
594 Chapter 12 Ideal Gas Mixture and Psychrometric Applications

 12.8.1 Applying Mass and Energy Balances to

Air-Conditioning Systems

The object of this section is to illustrate the use of the conservation of mass and conserva-

tion of energy principles in analyzing systems involving mixtures of dry air and water vapor

in which a condensed water phase may be present. The same basic solution approach that

has been used in thermodynamic analyses considered thus far is applicable. The only new

aspect is the use of the special vocabulary and parameters of psychrometrics.

Systems that accomplish air-conditioning processes such as heating, cooling, humidifica-

tion, or dehumidification are normally analyzed on a control volume basis. To consider a typ-

ical analysis, refer to Fig. 12.10, which shows a two-inlet, single-exit control volume at steady

state. A moist air stream enters at 1, a moist air stream exits at 2, and a water-only stream

enters at 3. The water-only stream may be a liquid or a vapor. Heat transfer at the rate

can occur between the control volume and its surroundings. Depending on the application,

the value of might be positive, negative, or zero.

MASS BALANCE. At steady state, the amounts of dry air and water vapor contained within

the control volume cannot vary. Thus, for each component individually it is necessary for the

total incoming and outgoing mass flow rates to be equal. That is

For simplicity, the constant mass flow rate of the dry air is denoted by . The mass flow

rates of the water vapor can be expressed conveniently in terms of humidity ratios as

and . With these expressions, the mass balance for water becomes

(12.52)

When water is added at 3, 

is greater than 

ENERGY BALANCE. Assuming and ignoring all kinetic and potential energy ef-

fects, the energy rate balance reduces at steady state to

(12.53)

In this equation, the entering and exiting moist air streams are regarded as ideal gas mixtures

of dry air and water vapor.

Equation 12.53 can be cast into a form that is particularly convenient for the analysis of

air-conditioning systems. First, with Eq. 12.47 the enthalpies of the entering and exiting water

vapor can be evaluated as the saturated vapor enthalpies corresponding to the temperatures

and T

, respectively, giving

Then, with and , the equation can be expressed as

(12.54)0  Q

 m

 v

2 m

 m

 v

 v

0  Q

 1m

 m

2 m

 1m

 m

0  Q

 1m

 m

2 m

 1m

 m

 0

 m

 v

1water2

 v

 m

 m

1water2

 m

1dry air2

Liquid or vapor, m

Boundary

Moist air

, m

 Figure 12.10 System for conditioning

moist air.

12.8 Analyzing Air-Conditioning Processes 595

Finally, introducing Eq. 12.52, the energy rate balance becomes

(12.55)

The first underlined term of Eq. 12.55 can be evaluated from Tables A-22 giving the ideal

gas properties of air. Alternatively, since relatively small temperature differences are nor-

mally encountered in the class of systems under present consideration, this term can be eval-

uated as h

 h

 c

 T

), where c

is a constant value for the specific heat of dry

air. The second underlined term of Eq. 12.55 can be evaluated using steam table data to-

gether with known values for 

and 

MODELING SUMMARY. As suggested by the foregoing development, several simplifying

assumptions are commonly used when analyzing the air-conditioning systems under present

consideration. In addition to the assumption of steady-state operation, one-dimensional flow

is assumed to apply at locations where matter crosses the boundary of the control volume,

and the effects of kinetic and potential energy at these locations are neglected. In most cases

there is no work, except for flow work where matter crosses the boundary. Further simplifi-

cations also may be required in particular cases.

 12.8.2 Conditioning Moist Air at Constant Composition

Building air-conditioning systems frequently heat or cool a moist air stream with no change

in the amount of water vapor present. In such cases the humidity ratio  remains constant,

while relative humidity and other moist air parameters vary. Example 12.10 gives an ele-

mentary illustration using the methodology of Sec. 12.8.1.

0  Q

 m

31h

 h

2 v

 1v

 v

EXAMPLE 12.10 Heating Moist Air in a Duct

Moist air enters a duct at 10C, 80% relative humidity, and a volumetric flow rate of 150 m

/min. The mixture is heated as it

flows through the duct and exits at 30C. No moisture is added or removed, and the mixture pressure remains approximately

constant at 1 bar. For steady-state operation, determine (a) the rate of heat transfer, in kJ/min, and (b) the relative humidity

at the exit. Changes in kinetic and potential energy can be ignored.

SOLUTION

Known: Moist air that enters a duct at 10C and   80% with a volumetric flow rate of 150 m

/min is heated at constant

pressure and exits at 30C. No moisture is added or removed.

Find: Determine the rate of heat transfer, in kJ/min, and the relative humidity at the exit.

Schematic and Given Data:

)

Boundary

= 30°C

= 150

= 10°C

= 80%

(AV)

___

min

 Figure E12.10a