Момент инерции тела методом крутильных колебаний
Подождите немного. Документ загружается.

ФАО РФ
Вологодский Государственный Технический
Университет
Кафедра физики
физика
Лабораторная работа:
Измерение момента инерции тела методом крутильных колебаний.
Выполнили:!ст.!гр.!ФЭК-11
Волокитин А. А.
Сыроватский Д. Л.
Проверил:! Михайлов А. В.

Вологда
2008
Цель работы: ознакомление с экспериментальным методом измерения моментов инерции тел –
методом крутильных колебаний и экспериментальная проверка теории Штейнера.
Оборудование: лабораторная установка с секундомером и металлические грузы.
Теория вопроса.
Испытуемое твёрдое тело, имеющее вид диска радиуса R, подвешено на упругой
металлической проволоке так, что нижний конец проволоки проходит через центр тяжести диска,
а верхний закреплён. При повороте диска на некоторый угол
вокруг оси, в проволоке
возникают упругие силы, которые стремятся возвратить диск к положению равновесия. Момент M
упругих сил на основании закона Гука пропорционален углу поворота:
αKM
, (1)
где K – коэффициент пропорциональности, называемый модулем кручения. По второму закону
динамики для вращательного движения:
εJM
, (2)
где J – момент инерции диска относительно оси 00,
ε
– угловое ускорение. Из (1) и (2) получаем
уравнение для угла поворота:
0
2
2
αK
dt
ad
J
. (3)
Решением этого уравнения является:
t
J
K
αα cos
0
. (4)
В нём можно убедиться непосредственно подстановкой (4) в (3). Величина
J
K
есть круговая
частота крутильных колебаний, а их период T равен:
K
J
π
ω
π
T 2
2
. (5)
Из выражения (5) находим момент инерции тела:
2
2
4π
KT
J
. (6)
Для исключения из формулы (6) неизвестного модуля кручения поступают следующим
образом. На диск 1 симметрично на расстоянии «a» от центра помещают три дополнительных
груза массой m и радиусом r каждый. Эти грузы относительно оси 00 создают дополнительный
момент инерции J, который находится по теореме Штейнера и равен:
)
2
1
(3
23
mamrJ
. (7)
При этом период крутильных колебаний также изменится и станет равным
1
Т
. Таким образом,
для системы «диск с грузами» формула (6) примет вид:
2
2
1
1
4π
KT
JJJ
, (8)
где J – момент инерции диска без грузов. Поделив (8) на (6), исключаем К:
2
2
1
T
T
J
JJ
.
Подставляя сюда (7) для вычисления искомого момента инерции диска, окончательно получим:
22
1
2
22
)2(
2
3
TT
T
ramJ
. (9)
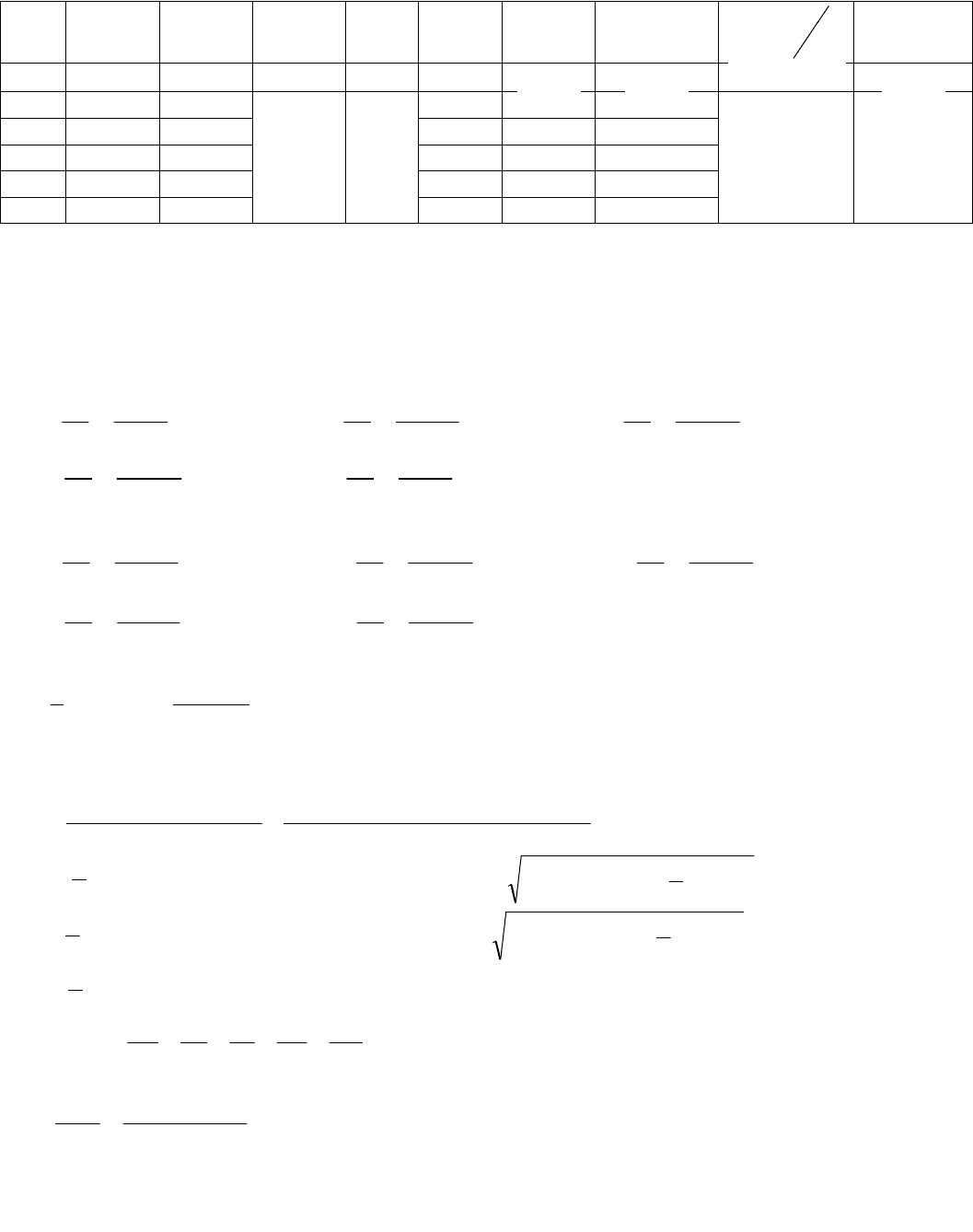
Измерение и обработка результатов.
№ T
'T
r a m J
cp
J
cp
cp
J
J
E
Δ
cp
JΔ
п/п с с м м кг
2
мкг
2
мкг
2
мкг
1 0,536 0,609
0,024 0,056
2,19 0,042 0,077
0,022 0,0015
2 0,54 0,63 2,19 0,04 0,062
3 0,542 0,62 2,19 0,067 0,073
4 0,534 0,609 2,19 0,067 0,075
5 0,535 0,644 2,19 0,067 0,05
ct 72,10
1
;
ct 81,10
2
;
ct 84,10
3
;
ct 84,10
4
;
ct 84,10
5
;
ct 18,12
1
;
сt 59,12
2
;
сt 41,12
3
;
сt 18,12
4
;
сt 87,12
3
;
мr 024,0
;
мa 056,0
;
кгmmm 73,0
321
;
кгmmmm 19,2
321
;
Периоды времени для тела без грузов.
c
t
T 536,0
20
72,10
20
1
1
;
c
c
t
T 54,0
20
81,10
20
2
2
;
c
c
t
T 542,0
20
84,10
20
3
3
;
c
c
t
T 534,0
20
68,10
20
4
4
;
c
c
t
T 535,0
20
7,10
20
5
5
;
Периоды времени для тела с грузами.
c
c
t
T 609,0
20
18,12
20
1
1
;
c
c
t
T 63,0
20
59,12
20
2
2
;
c
c
t
T 62,0
20
41,12
20
3
3
;
c
c
t
T 609,0
20
18,12
20
4
4
;
c
c
t
T 644,0
20
87,12
20
5
5
;
Момент инерции.
22/
2
22
)2(
2
3
TT
T
ramJ
;
2
1
077,0 мк гJ
;
2
2
062,0 мк гJ
;
2
3
073,0 мкгJ
;
2
4
075,0 мкгJ
;
2
5
05,0 мкгJ
;
2
54321
0674,0
5
05,0075,0073,0062,0077,0
5
мкг
JJJJJ
J
cp
;
)(0195,073,004,0
3
2
кгm
069,0)01,0
3
2
()3,4016,0(
22
T
)(000321,0027,002,0
3
2
мr
056,0)01,0
3
2
()3,4013,0('
22
T
)(00079,006,002.0
3
2
мa
2
0015,0)
'
'
( мкг
T
T
T
T
r
r
a
a
m
m
JJ
c pср
;
022,0
0674,0
0015,0
2
2
мкг
мкг
J
J
E
cp
cp
.
Вывод: я ознакомился с экспериментальным методом измерения моментов инерции тел – методом
крутильных колебаний и экспериментально проверил теорему Штейнера.
22
0015,00674,0 мкгмкгJ
.
