Могилев А.В., Пак Н.И., Хённер Е.К. Информатика
Подождите немного. Документ загружается.

PutPixel, а введя ее в цикл, изобразить график или траекторию. Если же требуется изобразить
движение тела, то перед выводом на экран очередной точки достаточно стереть предыдущую или
воспользоваться несколькими видеостраницами - соответствующие приемы программирования
читателю, скорее всего, известны. Отметим, что создание на экране дисплея динамических
зрительных изображений - так называемая анимация - одно из перспективных направлений
искусственного интеллекта-раздела современной информатики.
Изолинии. В задачах моделирования достаточно стандартная проблема - построение линий
(поверхностей), вдоль которых некоторая функция имеет одинаковое значение, называемых
изолиниями (изоповерхностями). Это очень распространенная задача визуализации характеристик
некоторого скалярного поля в приближении сплошной среды: изотермы - линии равной
температуры, изобары - линии равного давления, изолинии функции тока жидкости или газа, по
которым легко можно представить себе их потоки, изолинии численностей экологической
популяции на местности, изолинии концентрации вредных примесей в окружающей среде и т.д.
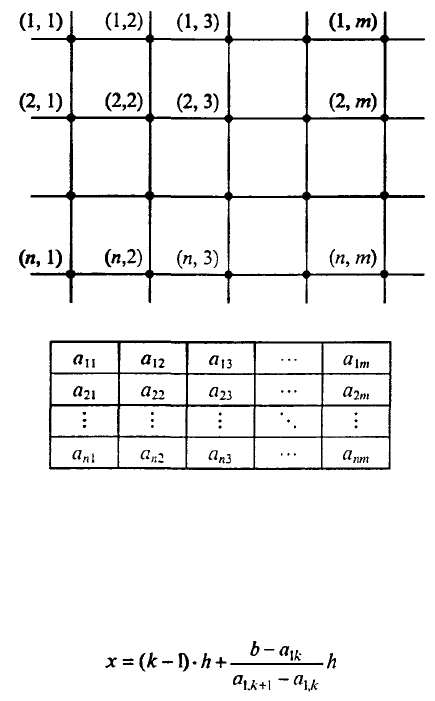
Опишем типичную процедуру построения изолиний на экране компьютера. На старте мы
имеем двумерную таблицу значений некоторой величины А, полученную в ходе математического
моделирования; числа в этой таблице соответствуют значениям этой величины в узлах
пространственной сетки (рис. 7.5).
Зададим некоторый, совершенно условный, пространственный шаг h между соседними
узлами по горизонтали и вспомогательную систему координат, в которой узел (1, 1) имеет
координату (0, 0), узел (1, 2) - координату (h, 0), узел (1, 3) - координату (2h, 0) и т.д. Если шаг по
вертикали h*, то узел (i, j) в этой системе имеет координату ((i-1) ∙ h, (y-1) ∙ h*).
Предварительно найдем в таблице наибольшее и наименьшее значения величин а
ij
-
допустим, это a
min
и а
mах
. Пусть b - некоторое промежуточное значение: a
min
< b < a
max
. Обсудим в
общих чертах, как построить изолинию A = b. Будем для этого (в цикле) просматривать вначале
все пары ближайших чисел в первой строке таблицы в поисках такой пары, для которой b
находится «внутри». Допустим, число b находится между a
1k
и a
1,k+1
, т.е. либо a
1k
< b < a
1,k+1
, либо
a
1k
> b > a
1,k+1
.
Рис. 7.5. Пространственная сетка и соответствующая ей таблица значений величины А
С помощью линейной интерполяции найдем соответствующую горизонтальную
координату точки, в которой А = b:
(координата у определяется номером горизонтальной линии; в данном случае у = 0).
591
Найденные координаты запомним и просмотрим первую строку в таблице до конца, затем
просмотрим вторую строку и т.д. Покончив с просмотром строк, мы получим часть точек,
соответствующих изолинии А = b.
После этого займемся просмотром столбцов. Допустим, во втором столбце нашлась пара
чисел, для которой число b находится между а
p2
и a
p+1,2
. Она дает следующую точку для изолинии.
Закончив просмотр всех столбцов, мы получим максимально возможный набор координат точек,
принадлежащих данной изолинии. Выведя их на экран в нужном масштабе, получим точечное
изображение изолинии А = b, после чего можем, взяв другое значение b, построить следующую
изолинию. Более детально эта процедура изложена ниже в пункте 3.8 на примере построения
линий равного потенциала электрического поля.
Условные цвета, условное контрастирование. Еще один интересный прием современной
научной графики - условная раскраска. Она находит широчайшее применение в самых разных
приложениях науки и представляет собой набор приемов по максимально удобной, хотя и очень
условной, визуализации результатов компьютерного моделирования.
Приведем примеры. В различных исследованиях температурных полей встает проблема
наглядного представления результатов. Самый простой (и, с точки зрения специалиста, весьма
неэффективный) - привести карту (чертеж, план), в некоторых точках которой обозначены
значения температуры.
Другой способ - набор изотерм - гораздо эффективнее; к нему прибегают некоторые газеты,
давая состояние и прогноз погоды. Но можно добиться еще большей наглядности, учитывая, что
большинству людей свойственно, сравнивая разные цвета, воспринимать красный как «горячий»,
голубой как «холодный», а все остальные - между ними. Допустим, что на некоторой территории
температура в данный момент имеет в разных местах значения от -25°С до + 15°С. Разделим этот
диапазон на участки с шагом, равным, например, 5°
[-25,-20], [-20,-15],...,[+10,+15],
и закрасим первый из них в ярко-голубой, последний - в ярко-красный, а все остальные - в
промежуточные оттенки голубого и красного цветов. Получится замечательная наглядная картина
температурного поля.
А что делать, если дисплей монохромный?! Или если изображение надо перенести с
цветного дисплея на бумагу при отсутствии возможности цветной печати? -Тогда роль цвета
может сыграть контраст. Сделаем самый «горячий» участок самым темным, самый «холодный» -
прозрачным, а остальные - между ними. Эффектность, конечно, меньше, чем при цветовой
раскраске, но для наметанного глаза изображение информативно.
То же самое можно делать при иллюстрации температурного поля и на поверхности
обрабатываемой на станке детали, и на поверхности далекой планеты.
В нашем курсе есть несколько моделей, в которых можно (и очень полезно) прибегнуть к
подобному приему визуализации. В задаче о теплопроводности в стержне это даже не очень
сложно; можно делать такие условные раскраски при моделировании распределения
электрических полей. Если заниматься имитационным моделированием конкурирующих
популяций, то, раскрасив их в разные цвета, можно получить на экране причудливые картины,
передающие ход конкурентной борьбы.
Условные раскраски бывают и гораздо более абстрактными, чем в описанных выше
случаях. При моделировании сложных органических молекул компьютер может выдавать
результаты в виде многоцветной картины, на которой атомы водорода изображены одним цветом,
углерода - другим и т.д., причем атом представлен шариком (кружочком), в пределах которого
плотность цвета меняется в соответствии с распределением электронной плотности.
При поиске полезных ископаемых методами аэрофотосъемки с самолетов или космических
спутников компьютеры строят условные цветовые изображения распределений плотности под
поверхностью Земли. Подобных примеров можно привести достаточно много.
Подведем итог: изображения в условных цветах и контрастах - мощнейший прием научной
графики. Он позволяет понять строение не только плоских, но и объемных (трехмерных) объектов,
дает в руки исследователя один из замечательных методов познания. Приведем в качестве
иллюстрации фрагмент программы.
592
Программа 147. Условная раскраска неравномерно нагретого стержня в разные моменты
времени (по заранее заготовленным данным).
Program Stergen;
Uses Crt, Graph
Type Mas2 = Array [0..10, 0..4] of Real;
Const (Массив распределения температуры в разные моменты времени)
U : Mas2 =
((3.000, 3.667, 4.333, 5.000, 3.000), (3.000, 3.628, 4.128, 3.952, 3.000),
(3.000, 3.514, 3.783, 3.593, 3.000), (3.000, 3.377, 3.546, 3.396, 3.000),
(3.000, 3.267, 3.381, 3.272, 3.000), (3.000, 3.187, 3.266, 3.188, 3.000),
(3.000, 3.131, 3.185, 3.131, 3.000), (3.000, 3.091, 3.129, 3.091, 3.000),
(3.000, 3.064. 3.090, 3.064, 3.000), (3.000, 3.044, 3.063, 3.044, 3.000),
(3.000, 3.031, 3.044, 3.031, 3.000));
Var
M, I, J, N1, Nt : Integer; MaxF, L, T, HI, Ht : Real;
Procedure Initialize; (Процедура инициализации графического режима)
Var GraphDriver, GraphMode : Integer;
Begin
DetectGraph(GraphDriver, GraphMode) ;
InitGraph(GraphDriver, GraphMode, '');
End;
(Графическая иллюстрация решения)
Procedure Postar.ovka (U : Mas2; Nt, N1 : Integer; HI, L, MaxF : Real);
Var X_N, Shag, Y_N, Shir, Dlin, Color, I, J, K, Y : Integer;
Flag .: Boolean; Ff : String; Col : Array [0..15] Of Byte;
Begin
Initialize; (Инициализация графического режима)
X_N := GetMaxX Div 6;
If Nt <= 6 Then M := Nt Else M := Nt Div 2;
Y_N := GetMaxY Div M - 20; Shir := Y_N Div 2;
Dlin := GetMaxX -2 * X_N; Shag := Trunc(Dlin / N1); Str(Shag,Ff) ;
Col[0] := 0; Col[l] := 8; Col[2] := 1; (Палитра цветов)
Col[3] := 9; Col[4] := 3; Col[5] := 11;
Col[6] := 2; Col[7] := 10; Col[8] := 14;
Col[9] := 13; Col[l0] := 5; Col[ll] := 12; Col [12] := 4;
For I :== 0 To M - 1 Do (номер временного промежутка)
Begin
For J := 0 To N1 - 1 Do (номер участка стержня)
Begin
Flag := False;
For К := 0 To Shag Do
Begin
For y:= 0 To Shir Do
Begin
Color := 1 + Round((U[I, J] + (определение номера цвета)
(U[I, J + 1] - U[I, J]) * К / Shag - U[0, 0]) / 3 * 16);
If Random(64) > 32
Then If Random(64) > 32 Then Color := Color + 1 Else
Color := Color - 1;
If Not Flag Then (вывод текущей температуры)
Begin
Str((U[I,J]+(U(I,J+l]-U[I,J])*K/Shag) : 5 : 3, Ff);
OutTextXY(K+X_N+Shag*J, Y_N*(1+1)-19, Ff) ;
Flag := True
End;
{рисование точки}
PutPixel(K+X_N+Shag*J, Y+Y_N*(1+I), Col[Color])
End
593
End
End
End;
SetColor(White); OutTextXY(150, 450, 'Нажмите любую клавишу ');
Repeat Until KeyPressed; CloseGraph
End;
Begin (ОСНОВНАЯ ПРОГРАММА)
L := 4; Т := 10; Hi := 1; Ht := 1;
N1 := Trunc(L / HI); Nt := Trunc(T / Ht); MaxF := 5;
Postanovka (U. Nt, N1, HI, L, MaxF)
End.
§3. МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ
3.1. ФИЗИКА И МОДЕЛИРОВАНИЕ
Физика - наука, в которой математическое моделирование является чрезвычайно важным
методом исследования. Наряду с традиционным делением физики на экспериментальную и
теоретическую сегодня уверенно выделяется третий фундаментальный раздел - вычислительная
физика (computational physics). Причину этого в целом можно сформулировать так: при
максимальном проникновении в физику математических методов, порой доходящем до
фактического сращивания этих наук, реальные возможности решения возникающих
математических задач традиционными методами очень ограниченны. Из многих конкретных
причин выделим две наиболее часто встречающиеся: нелинейность многих физических процессов
(примеры - ниже в тексте) и необходимость исследования совместного движения многих тел, для
которого приходится решать системы большого числа уравнений. Часто численное моделирование
в физике называют вычислительным экспериментом, поскольку оно имеет много общего с
лабораторным экспериментом.
Таблица 7.1
Аналогии между лабораторным и вычислительным экспериментами
Лабораторный эксперимент Вычислительный эксперимент
Образец
Физический прибор
Калибровка прибора
Измерение .
Анализ данных
Модель
Программа для компьютера
Тестирование программы
Расчет
Анализ данных
Численное моделирование (как и лабораторные эксперименты) чаще всего является
инструментом познания качественных закономерностей природы. Важнейшим его этапом, когда
расчеты уже завершены, является осознание результатов, представление их в максимально
наглядной и удобной для восприятия форме. Забить числами экран компьютера или получить
распечатку тех же чисел не означает закончить моделирование (даже если числа эти верны). Тут
на помощь приходит другая замечательная особенность компьютера, дополняющая способность к
быстрому счету - возможность визуализации абстракций. Представление результатов в виде
графиков, диаграмм, траекторий движения динамических объектов в силу особенностей
человеческого восприятия обогащает исследователя качественной информацией. Во многих
рассматриваемых ниже физических задачах фундаментальную роль играет второй закон Ньютона
- основа всей динамики:
594

В уточненной редакции закон утверждает: ускорение, с которым движется тело в данный
момент времени, пропорционально действующей на него в этот момент силе и обратно
пропорционально имеющейся в данный момент у тела массе.
Разные записи этого утверждения:
Связывая мгновенные значения величин, второй закон Ньютона позволяет изучать
движение тел при произвольных изменениях во времени силы и массы.
3.2. СВОБОДНОЕ ПАДЕНИЕ ТЕЛА С УЧЕТОМ СОПРОТИВЛЕНИЯ СРЕДЫ
При реальных физических движениях тел в газовой или жидкостной среде трение
накладывает огромный отпечаток на характер движения. Каждый понимает, что предмет,
сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не
движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды.
Даже эту. относительно несложную, задачу нельзя решить средствами «школьной» физики; таких
задач, представляющих практический интерес, очень много. Прежде чем приступать к
обсуждению соответствующих моделей, вспомним, что известно о силе сопротивления.
Закономерности, обсуждаемые ниже, носят эмпирический характер и отнюдь не имеют
столь строгой и четкой формулировки, как второй закон Ньютона. О силе сопротивления среды
движущемуся телу известно, что она, вообще говоря, растет с ростом скорости (хотя это
утверждение не является абсолютным). При относительно малых скоростях величина силы
сопротивления пропорциональна скорости и имеет место соотношение F
coпp
= k
1
v, где k
1
определяется свойствами среды и формой тела. Например, для шарика k
1
= 6πμr - это формула
Стокса, где μ -динамическая вязкость среды, r - радиус шарика. Так, для воздуха при t = 20°С и
давлении 1 атм.μ = 0,0182 Н∙с∙м
-2
, для воды 1,002 Н∙с∙м
-2
, для глицерина 1480 Н∙с∙м
-2
.
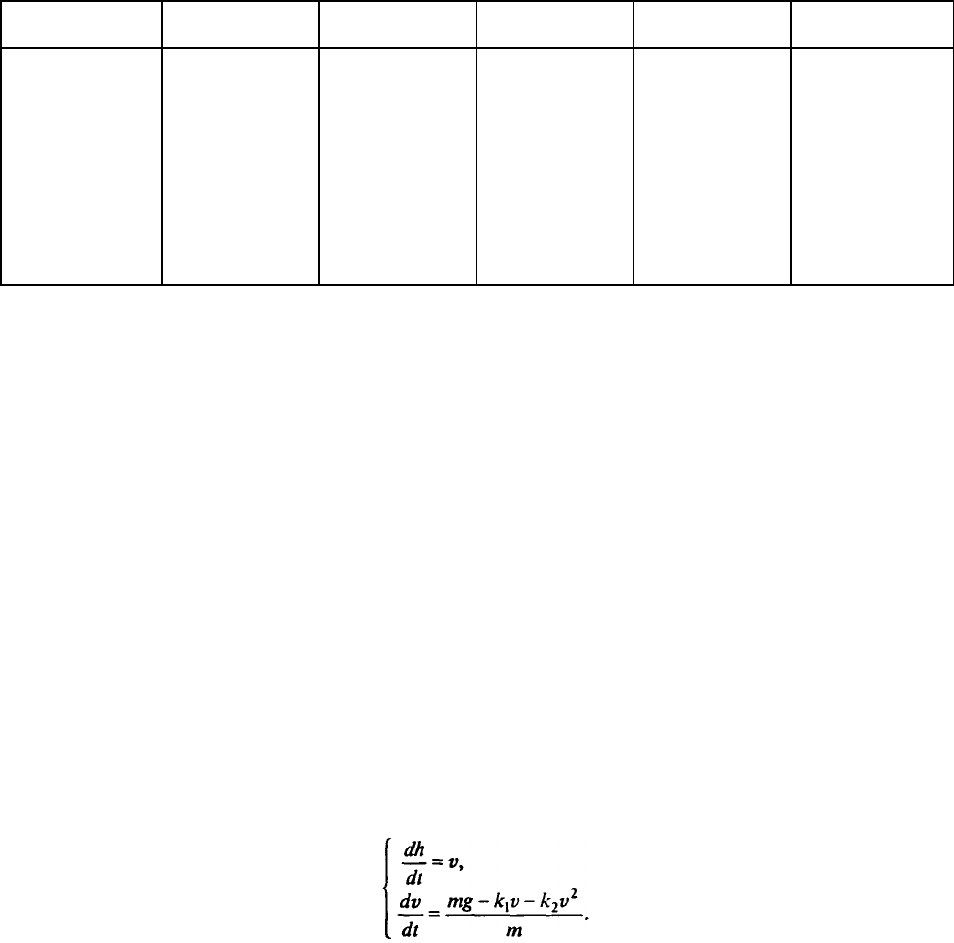
Оценим, при какой скорости для падающего вертикально шара сила сопротивления
сравняется с силой тяжести (и движение станет равномерным).
Имеем
или
Пусть r = 0,1 м, ρ = 0,8∙10
3
кг/м
3
(дерево). При падении в воздухе v* ≈ 960 м/с, в воде v*≈ 17
м/с, в глицерине v* ≈ 0,012 м/с.
На самом деле первые два результата совершенно не соответствуют действительности.
Дело в том, что уже при гораздо меньших скоростях сила сопротивления становится
пропорциональной квадрату скорости: F
coпp
= k
2
v
2
. Разумеется, линейная по скорости часть силы
сопротивления формально также сохранится, но если k
2
v
2
>> k
1
v, то вкладом k
1
v можно пренебречь
(это конкретный пример ранжирования факторов). О величине k
2
известно следующее: она
пропорциональна площади сечения тела S, поперечного по отношению к потоку, и плотности
среды ρ
среды
и зависит от формы тела. Обычно представляют k
2
= 0,5сSρ
срeды
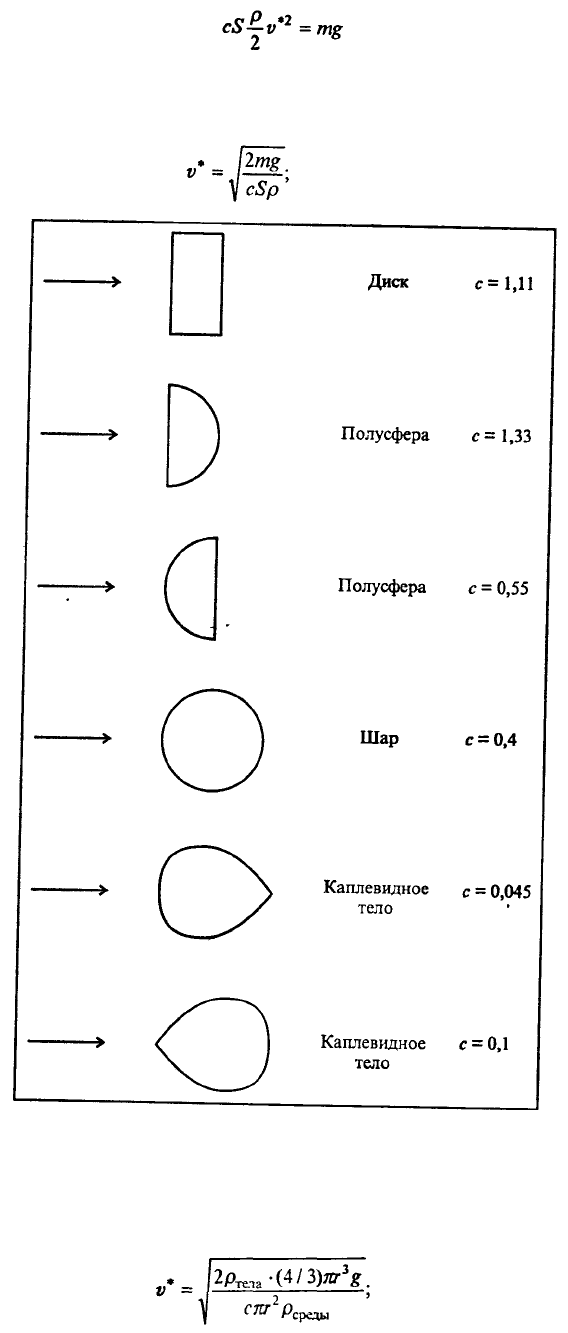
, где с - коэффициент
лобового сопротивления - безразмерен. Некоторые значения с (для не очень больших скоростей)
приведены на рис. 7.6.
При достижении достаточно большой скорости, когда образующиеся за обтекаемым телом
вихри газа или жидкости начинают интенсивно отрываться от тела, значение с в несколько раз
уменьшается; для шара оно становится приблизительно равным 0,1. Подробности можно найти в
специальной литературе.
595
Вернемся к указанной выше оценке, исходя из квадратичной зависимости силы
сопротивления от скорости.
Имеем
или
(7.4)
Рис. 7.6. Значения коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых
имеет указанную на рисунке форму (см. книгу П.А.Стрелкова)
Для шарика
(7.5)
Примем r = 0,1 м, ρ = 0,8∙10
3
кг/м
3
(дерево). Тогда для движения в воздухе (ρ
возд
= 1,29 кг/м
3
)
получаем v* ≈ 18 м/с, в воде (ρводы ≈ 1∙10
3
кг/м
3
) v* ≈ 0,65 м/с, в глицерине (ρ
глицерина
= 1,26∙10
3
кг/
596
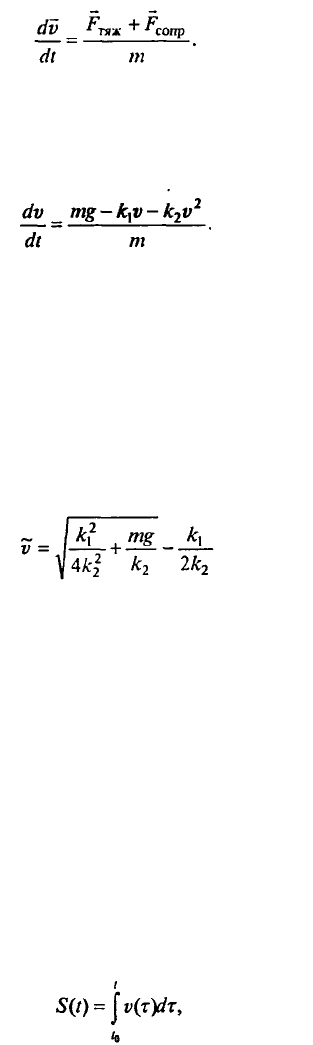
м
3
) v* ≈ 0,58 м/с.
Сравнивая с приведенными выше оценками линейной части силы сопротивления, видим,
что для движения в воздухе и в воде ее квадратичная часть сделает движение равномерным
задолго до того, как это могла бы сделать линейная часть, а для очень вязкого глицерина
справедливо обратное утверждение. Рассмотрим свободное падение с учетом сопротивления
среды. Математическая модель движения - уравнение второго закона Ньютона с учетом двух сил,
действующих на тело; силы тяжести и силы сопротивления среды:
(7.6)
Движение является одномерным; проецируя векторное уравнение на ось, направленную
вертикально вниз, получаем
(7.7)
Вопрос, который мы будем обсуждать на первом этапе, таков: каков характер изменения
скорости со временем, если все параметры, входящие в уравнение (7.7), заданы? При такой
постановке модель носит сугубо дескриптивный характер. Из соображений здравого смысла ясно,
что при наличии сопротивления, растущего со скоростью, в какой-то момент сила сопротивления
сравняется с силой тяжести, после чего скорость больше возрастать не будет. Начиная с этого
момента, dv/dt = 0, и соответствующую установившуюся скорость
v
~
можно найти из условия mg
– k
1
v – k
2
v
2
= 0 , решая не дифференциальное, а квадратное уравнение. Имеем
(7.8)
(второй - отрицательный - корень, естественно, отбрасываем). Итак, характер движения
качественно таков: скорость при падении возрастает от v
0
до
v
~
; как и по какому закону - это
можно узнать, лишь решив дифференциальное уравнение (7.7).
Однако, даже в столь простой задаче мы пришли к дифференциальному уравнению,
которое не относится ни к одному из стандартных типов, выделяемых в учебниках по
дифференциальным уравнениям, допускающих очевидным образом аналитическое решение. II
хотя это не доказывает невозможность его аналитического решения путем хитроумных
подстановок, но они не очевидны (один из лучших помощников в их поиске - справочник Камке).
Допустим, однако, что нам удастся найти такое решение, выраженное через суперпозицию
нескольких алгебраических и трансцендентных функций - а как найти закон изменения во времени
перемещения? - Формальный ответ прост:
(7.9)
но шансы на реализацию этой квадратуры уже совсем невелики. Дело в том, что класс привычных
нам элементарных функций очень узок, и совершенно стандартна ситуация, когда интеграл от
суперпозиции элементарных функций не может быть выражен через элементарные функции в
принципе. Математики давно расширили множество функций, с которыми можно работать почти
так же просто, как с элементарными (т.е. находить значения, различные асимптотики, строить
графики, дифференцировать, интегрировать). Тем, кто знаком с функциями Бесселя, Лежандра,
интегральными функциями и еще двумя десятками других, так называемых, специальных
функций, легче находить аналитические решения задач моделирования, опирающихся на аппарат
597
дифференциальных уравнений. Однако даже получение результата в виде формулы не снимает
проблемы представления его в виде, максимально доступном для понимания, чувственного
восприятия, ибо мало кто может, имея формулу, в которой сопряжены логарифмы, степени, корни,
синусы и тем более специальные функции, детально представить себе описываемый ею процесс -а
именно это есть цель моделирования.
В достижении этой цели компьютер - незаменимый помощник. Независимо от того, какой
будет процедура получения решения - аналитической или численной, -задумаемся об удобных
способах представления результатов. Разумеется, колонки чисел, которых проще всего добиться
от компьютера (что при табулировании формулы, найденной аналитически, что в результате
численного решения дифференциального уравнения), необходимы; следует лишь решить, в какой
форме и размерах они удобны для восприятия. Слишком много чисел в колонке быть не должно,
их трудно будет воспринимать, поэтому шаг, с которым заполняется таблица, вообще говоря,
гораздо больше шага, с которым решается дифференциальное уравнение в случае численного
интегрирования, т.е. далеко не все значения v и S, найденные компьютером, следует записывать в
результирующую таблицу (табл. 7.2).
Таблица 7.2
Зависимость перемещения и скорости падения «безпарашютиста» от времени (от 0 до 15 с)
t(c) S(M) v (м/с) t(с) S(м) v (м/с)
0 0 0 8 200,1 35,6
1
4,8
9,6
9
235,9
36,0
2
18,7
17,9
10
272,1
36,3
3
40,1
24,4
11
308,5
36,4
4
66,9
28,9
12
345,0
36,5
5 97,4 31,9 13 381,5 36,6
6
130,3
33,8
14
418.1
36,6
7 164,7 35,0 15 454,7 36,6
Кроме таблицы необходимы графики зависимостей v(t) и S(t); по ним хорошо видно, как
меняются со временем скорость и перемещение, т.е. приходит качественное понимание процесса.
Еще один элемент наглядности может внести изображение падающего тела через равные
промежутки времени. Ясно, что при стабилизации скорости расстояния между изображениями
станут равными. Можно прибегнуть и к цветовой раскраске - приему научной графики,
описанному выше.
Наконец, можно запрограммировать звуковые сигналы, которые подаются через каждый
фиксированный отрезок пути, пройденный телом - скажем, через каждый метр или каждые 100
метров - смотря по конкретным обстоятельствам. Надо выбрать интервал так, чтобы вначале
сигналы были редкими, а потом, с ростом скорости, сигнал слышался все чаще, пока промежутки
не сравняются. Таким образом, восприятию помогают элементы мультимедиа. Поле для фантазии
здесь велико.
Приведем конкретный пример решения задачи о свободно падающем теле. Герой
знаменитого фильма «Небесный тихоход» майор Булочкин, упав с высоты 6000 м в реку без
парашюта, не только остался жив, но даже смог снова летать. Попробуем понять, возможно ли
такое на самом деле или же подобное случается только в кино. Учитывая сказанное выше о
математическом характере задачи, выберем путь численного моделирования. Итак,
математическая модель выражается системой дифференциальных уравнений
(7.10)
Разумеется, это не только абстрактное выражение обсуждаемой физической ситуации, но и
598
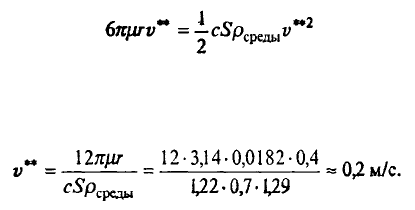
сильно идеализированное, т.е. ранжирование факторов перед построением математической
модели произведено. Обсудим, нельзя ли произвести дополнительное ранжирование уже в рамках
самой математической модели с учетом конкретно решаемой задачи, а именно - будет ли влиять
на полет парашютиста линейная часть силы сопротивления и стоит ли ее учитывать при
моделировании.
Так как постановка задачи должна быть конкретной, мы примем соглашение, каким
образом падает человек. Он - опытный летчик и наверняка совершал раньше прыжки с
парашютом, поэтому, стремясь уменьшить скорость, он падает не «солдатиком», а лицом вниз,
«лежа», раскинув руки в стороны. Рост человека возьмем средний - 1,7 м, а полуобхват грудной
клетки выберем в качестве характерного расстояния - это приблизительно 0,4 м. Для оценки
порядка величины линейной составляющей силы сопротивления воспользуемся формулой Стокса.
Для оценки квадратичной составляющей силы сопротивления мы должны определиться со
значениями коэффициента лобового сопротивления и площадью тела. Выберем в качестве
коэффициента число с = 1,2 как среднее между коэффициентами для диска и для полусферы
(выбор для качественной оценки правдоподобен). Оценим площадь: S = 1,7∙0,4=0,7 (м
2
).
Выясним, при какой скорости сравняются линейная и квадратичная составляющие силы
сопротивления. Обозначим эту скорость v**. Тогда
или
Ясно, что практически с самого начала скорость падения майора Булочкина гораздо
больше, и поэтому линейной составляющей силы сопротивления можно пренебречь, оставив лишь
квадратичную составляющую.
После оценки всех параметров можно приступить к численному решению задачи. При этом
следует воспользоваться любым из известных численных методов интегрирования систем
обыкновенных дифференциальных уравнений: методом Эйлера, одним из методов группы Рунге -
Кутта, одним из многочисленных неявных методов. Разумеется, у них разная устойчивость,
эффективность и т.д. - эти сугубо математические проблемы здесь не обсуждаются. Программа,
реализующая метод Рунге - Кутта четвертого порядка, может быть взята из примера,
приведенного в следующем параграфе или из какого-нибудь стандартного пакета математических
программ.
Отметим, что существует немало программ, моделирующих простые физические процессы
типа рассматриваемого. У них реализован, в той или иной мере профессионально, диалоговый
интерфейс, позволяющий вводить параметры, получать на экране таблицы, графики, движущиеся
изображения. Однако в них, как правило, остаются скрытыми физические законы, определяющие
процесс, ограничения модели, возможности ее усовершенствования. Такие программы полезны
скорее как сугубо иллюстративные.
Вычисления производились до тех пор, пока «безпарашютист» не опустился на воду.
Примерно через 15 с после начала полета скорость стала постоянной и оставалась такой до
приземления (рис. 7.7). Отметим, что в рассматриваемой ситуации сопротивление воздуха
радикально меняет характер движения; при отказе от его учета график скорости, изображенный на
рисунке, заменился бы касательной к нему в начале координат.
599
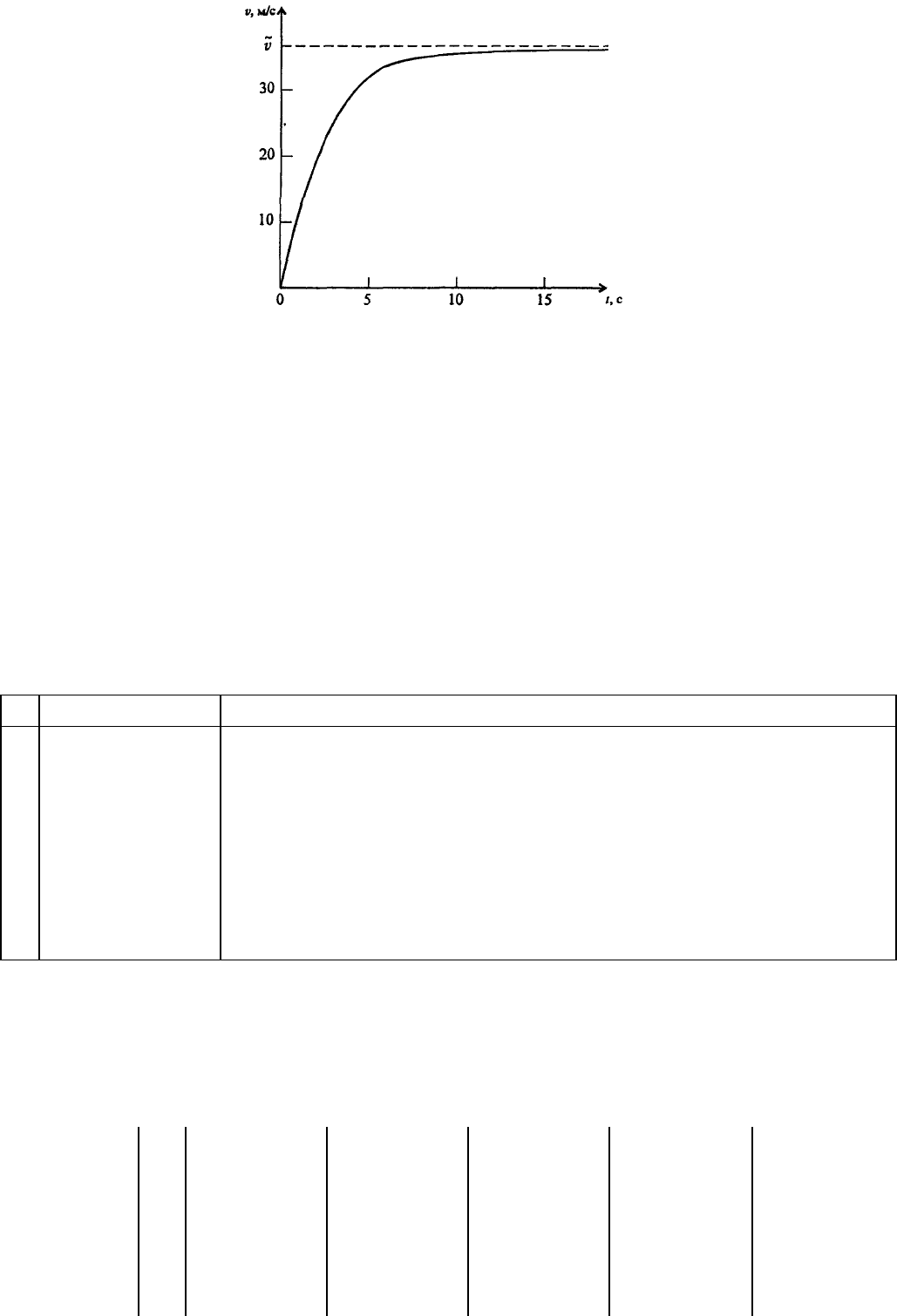
Рис. 7.7. График зависимости скорости падения «безпарашютиста» от времени
В некоторых случаях для ускорения процесса работы над какой-либо задачей
целесообразно вместо составления программы воспользоваться готовой прикладной программой
(например, табличным процессором). Покажем это на примере рассматриваемой задачи. В табл.
7.3 представлен небольшой фрагмент из табличного процессора Excel. Решение находится с
помощью, так называемого, исправленного метода Эйлера - одного из возможных вариантов
метода Рунге - Кутта второго порядка.
Кроме того, в ячейках D2, D4, D6 в таблице будем хранить соответственно значения шага
вычислений, массы «безпарашютиста», величины mg. Это связано с тем, что все константы также
удобно хранить в отдельных ячейках, чтобы в случае их изменения не пришлось переписывать
расчетные формулы. Достаточно записать
Таблица 7.3
Фрагмент таблицы, где представлено решение задачи о «безпарашютнсте»
А В
1 t v
2
3 0 0
4 =СУММ(АЗ; D2) =B3+D2/2* ( (D6-D8*B3^2) /D4+(D6-D8*(B3+D2*(D6-D8*B3^2)/D4)^2)/D4)
5 =СУММ(А4; D2) =B4+D2/2* ( (D6-D8*B4^2) /D4+(D6-D8* (B4+D2* (D6- D8*B4^2)/D4)^2)/D4)
6 =СУММ(А5; D2) =B5+D2/2*( (D6-D8*B5^2)/D4+(D6-D8*(B5+D2*(D6-D8*B5^2)/D4)^2)/D4)
7 =СУМM(А6; D2) =B6+D2/2* ( (D6-D8*B6^2) /D4+ (D6-D8* (B6+D2* (D6-D8*B6^2)/D4)^2)/D4)
8 =СУММ(А7; D2) =B7+D2/2*((D6-D8*B7^2)/D4+(D6-D8*(B7+D2*(D6-D8*B7^2)/D4)^2)/D4)
формулу правильно один раз, а затем скопировать в остальные ячейки, при этом, как известно, она
«настраивается» на соответствующую ячейку.
Таблица 7.4
Результаты вычислений, выполненных в табличном процессоре
А В С D
1 t v H
2
0,001
3
0
0
т
4
0,001
0,00981
80
5
0,002
0,01962
m*g
6
0,003
0,02943
784,8
7
0,004
0,03924
k2
600
