Мирзаянов М.Р. Паросочетания и смежные задачи (графы)
Подождите немного. Документ загружается.

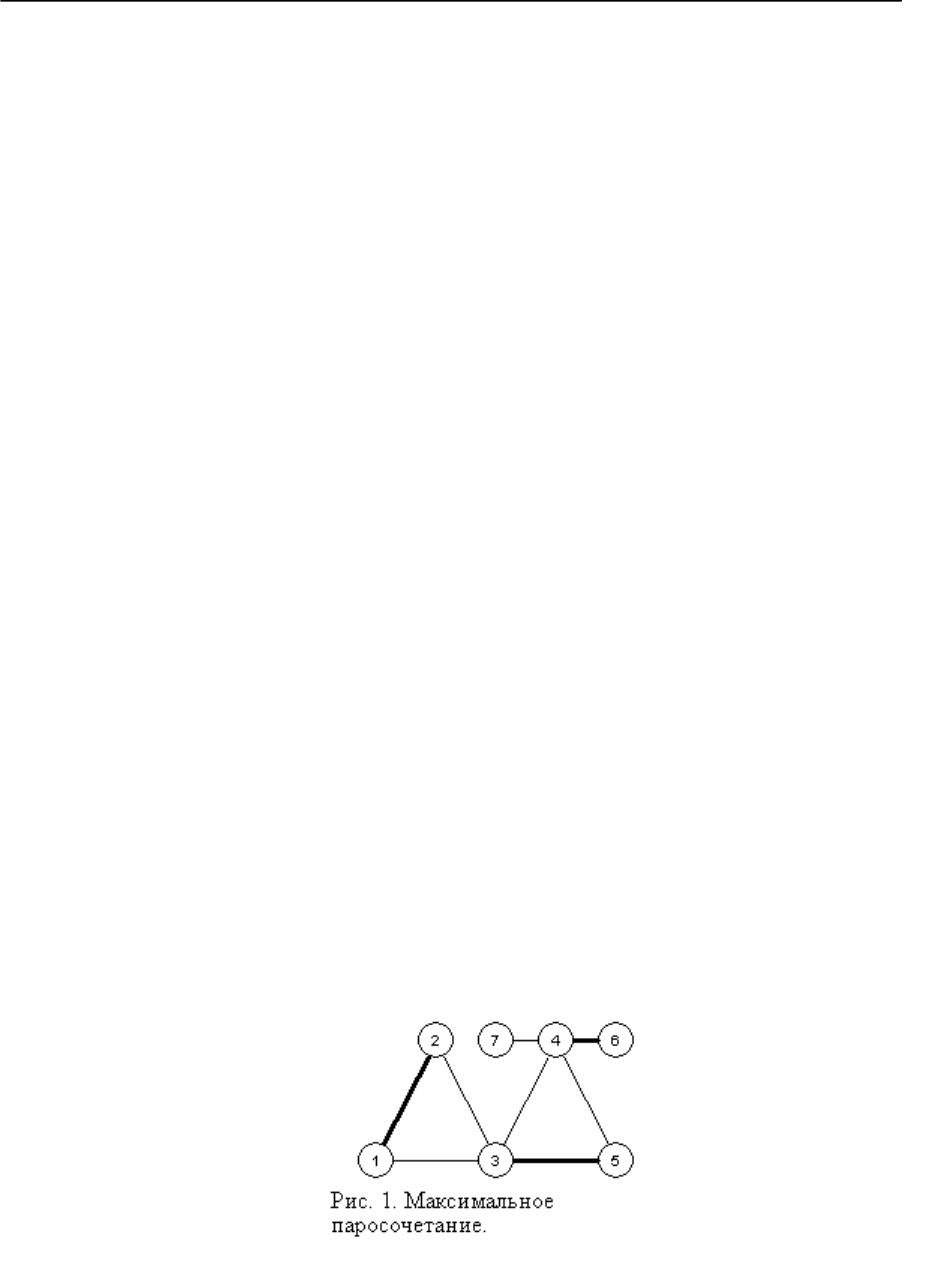
Мирзаянов М.Р. Паросочетания и смежные задачи
Мирзаянов М.Р.
Паросочетания и смежные задачи
§1. Определения и вводные понятия
Ниже под неориентированным графом, понимаем такой неориентированный граф, в
котором нет петель и кратных ребер. Графы будем обозначать символом
( , )G V E
,
подразумевая, что
V
– конечное непустое множество вершин, а
E
– множество
неупорядоченных пар из
V
(множество ребер графа).
Паросочетанием называется такое множество ребер графа
M E
, что каждая
вершина графа инцидентна не более чем одному ребру из
M
. Например, пустое
множество
M
является паросочетанием. Естественно пытаться искать паросочетания, в
которых наибольшее количество ребер.
Паросочетание
M
называется максимальным, если не существует такого
паросочетания
*
M
, что
*
| | | |M M
.
Следует заметить, что в некоторой русскоязычной литературе (например, см. [1])
придерживаются термина «наибольшее паросочетание», термином же «максимальное
паросочетание» называют такое паросочетание, которое не является собственным
подмножеством никакого другого паросочетания. В соответствии с более
употребительной последнее время терминологией, мы будем пользоваться термином
«максимальное паросочетание» в смысле количества ребер.
На рис. 1. изображен граф, для которого множество выделенных ребер образует
максимальное паросочетание.
1

Мирзаянов М.Р. Паросочетания и смежные задачи
Неориентированный граф называется двудольным, если множество его вершин
можно разбить на два таких подмножества, что не найдется ребра, соединяющей вершины
одного подмножества.
Известна следующая теорема.
Теорема 1 (критерий Кенига). Граф является двудольным тогда и только тогда,
когда все циклы в нем имеют четную длину.
Ниже часто двудольный граф мы будем обозначать символом
( , , )G X Y E
,
подчеркивая тем самым, что множество вершин графа разбито на два подмножества
X
и
Y
.
Например, граф изображенный на рис. 1 двудольным не является.
Заметим, что задача нахождения максимального паросочетания в двудольных графах
решается несколько проще, чем в произвольных графах.
Классической формулировкой такой задачи является следующая задача (задача о
бракосочетаниях). В ЗАГС поступило несколько заявок о бракосочетаниях. В каждую
заявку вписан некоторый юноша и некоторая девушка. В силу прогрессивности
современных взглядов один юноша (одна девушка) может содержаться более чем в одной
заявки. Так как по закону каждый супруг (супруга) может состоять лишь только в одном
союзе, возможно, что не все заявки можно удовлетворить. Какое наибольшее количество
заявок можно удовлетворить? Какие это заявки?
Если сконструировать граф такой, что юноши образуют вершины одной доли, а
девушки – вершины другой, каждую заявку рассматривать как ребро, то задача сводится к
поиску максимального паросочетания.
Вершины, инцидентные какому-либо ребру паросочетания, называются
насыщенными этим паросочетанием. Иногда так будем говорить и о ребрах, то есть
насыщенными будем называть ребра паросочетания.
В случае если паросочетание насыщает все вершины графа, такое паросочетание
будем называть совершенным (или 1-фактором).
2
Мирзаянов М.Р. Паросочетания и смежные задачи
§2. Четыре основные задачи
Первая основная задача была фактически уже сформулирована, и звучит она
следующим образом: в графе
( , )G V E
найдите максимальное паросочетание. В этой и
остальных задачах какого-либо поиска следует считать, что если ответов несколько, то
следует найти любой из них. Максимальное паросочетание будем обозначать символом
( )MM G
или просто
MM
, если контекст это позволяет (сокращение
MM
– аббревиатура
от английского maximum matching).
Подмножество ребер графа называется реберным покрытием, если любая вершина
графа инцидентна хотя бы одному ребру данного подмножества. Очевидно, интерес
представляют минимальные в некотором смысле реберные покрытия. Реберное покрытие
называется минимальным, если количество ребер в любом реберном покрытии не меньше,
чем в данном. Минимальное реберное покрытие будем обозначать как
( )MEC G
или
просто
MEC
(от англ. minimum edge covering). Заметим, что если в графе есть
изолированные вершины, то реберного покрытия для такого графа не существует.
Поэтому, везде ниже если ведется речь о реберном покрытии, предполагается, что в графе
нет изолированных вершин.
Вторая основная задача: в графе
( , )G V E
найдите
( )MEC G
.
Подмножество вершин графа называется независимым, если не существует ребра в
графе, оба конца которого принадлежат этому подмножеству. Независисимое
подмножество вершин называется максимальным, если не существует другого
независимого подмножества в котором больше вершин. Максимальное независимое
подмножество обозначается символом
( )MIVS G
или просто
MIVS
(от англ. maximum
independent vertex subset).
Третья основная задача: в графе
( , )G V E
найдите
( )MIVS G
.
3
Мирзаянов М.Р. Паросочетания и смежные задачи
Подмножество вершин графа называется вершинным покрытием, если для любого
ребра хотя бы один его конец инцидентен какой-то вершине подмножества. Вершинное
покрытие называется минимальным, если количество вершин в любом вершинном
покрытии не меньше, чем в данном. Минимальное вершинное покрытие будем обозначать
как
( )MVC G
или просто
MVC
(от англ. minimum vertex covering).
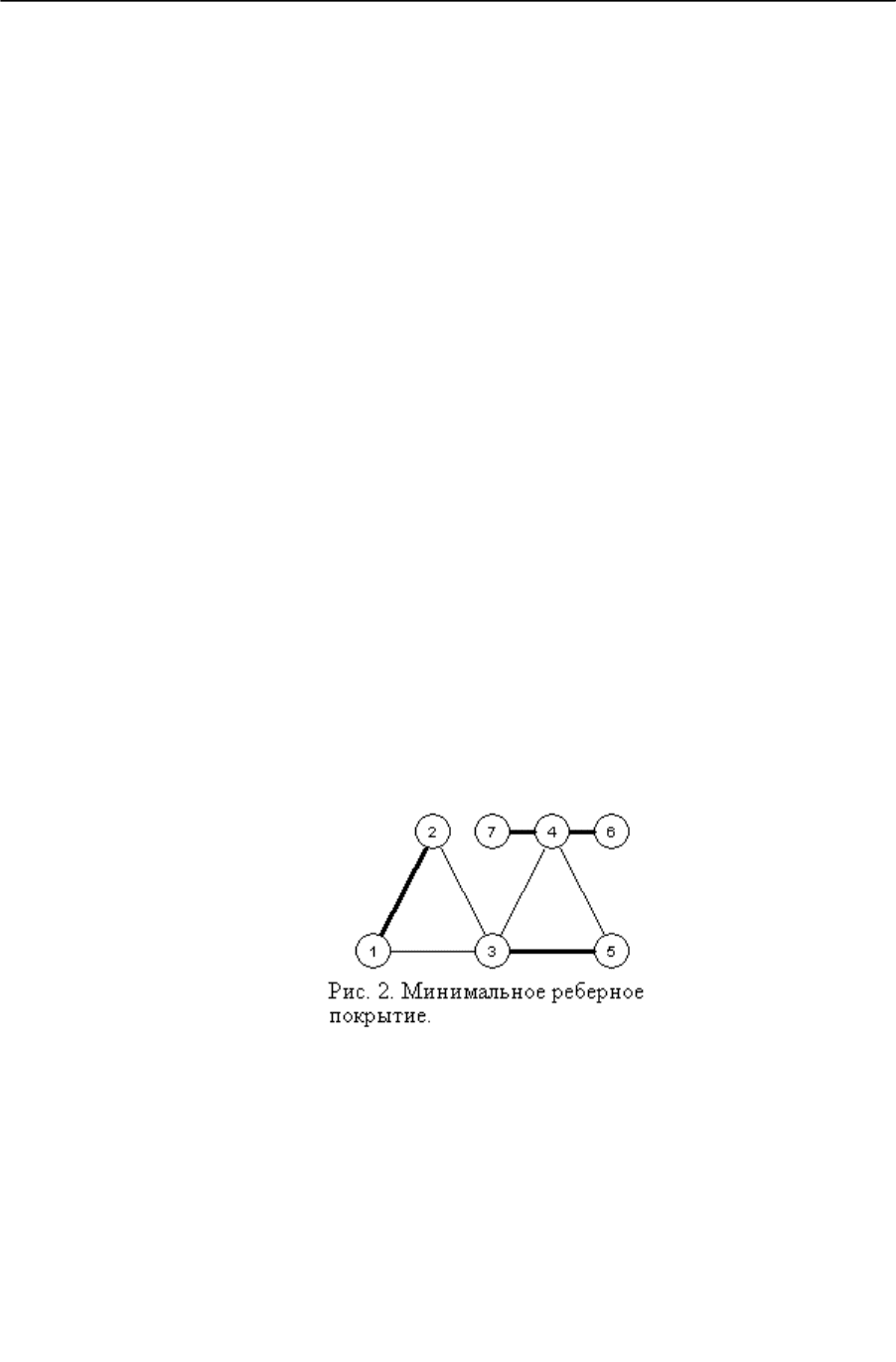
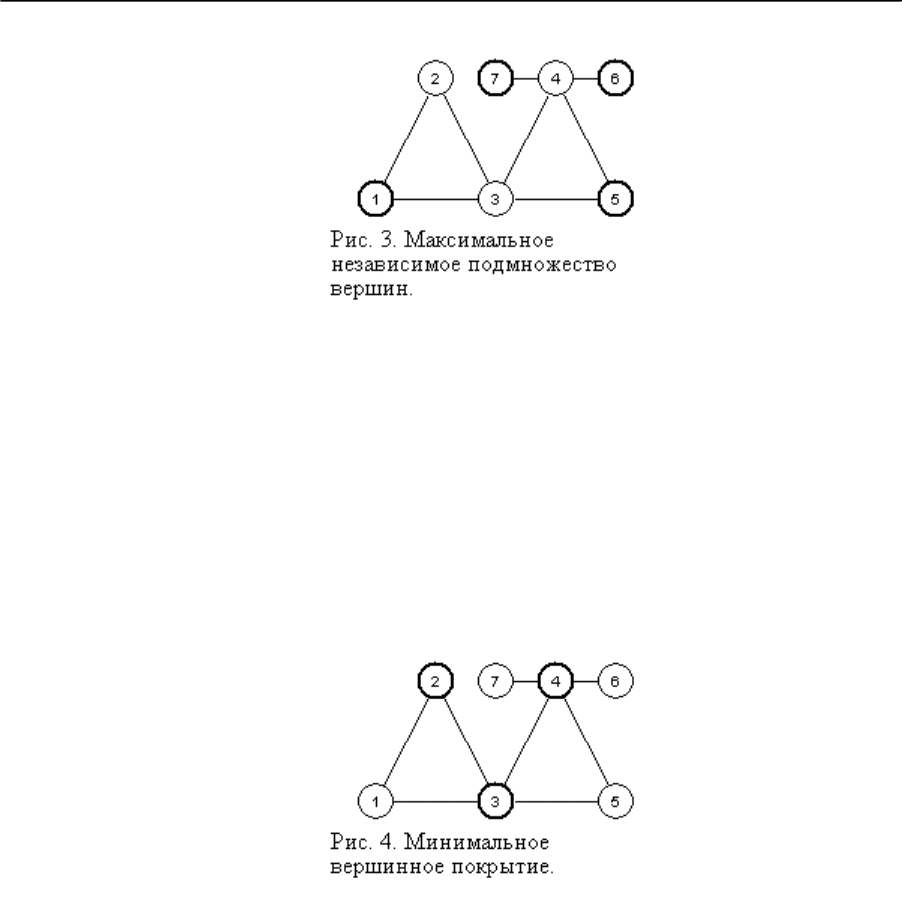
Напомним, что на рис.1 изображен пример решения первой основной задачи. На рис.
2, рис.3, рис. 4 изображены примеры решения задач 2, 3, 4 соответственно.
Следует заметить, что все эти четыре задачи являются классическими задачами
алгоритмической теории графов, и зачастую возникают в приложениях.
4

Мирзаянов М.Р. Паросочетания и смежные задачи
§3. Эквивалентность задач: MM и MEC, MIVS и MVC
В этом параграфе будет показано, что задачи нахождения максимального паросочетания и
минимального реберного покрытия являются эквивалентными. Решив любую из них,
легко получить решение другой задачи. Аналогично, решив задачу нахождения
максимального независимого подмножества вершин, немедленно следует решение задачи
нахождения минимального вершинного покрытия.
Теорема 2. Для любого графа
( , )G V E
выполняется равенство:
| ( ) | | ( ) | | |MIVS G MVC G V
.
Доказательство. Докажем более сильное утверждение: дополнение максимального
независимого подмножества вершин является минимальным вершинным покрытием
(разумеется, верно и обратное).
Рассмотрим произвольное максимальное независимое подмножество вершин
MIVS
V
.
Из определения независимого подмножества вершин следует, что любое ребро соединяет
либо вершину из
MIVS
и
\V MIVS
, либо вершины множества
\V MIVS
. Таким образом,
каждое ребро инцидентно некоторой вершине множества
\V MIVS
, то есть
\V MIVS
является некоторым вершинным покрытием. Следовательно:
| | | \ |MVC V MIVS
,
или:
| | | | | | .MVC MIVS V
Рассмотрим произвольное минимальное вершинное покрытие
MVC
. Так как каждое
ребро инцидентно хотя бы одной вершине из
MVC
, то
\V MVC
является независимым
подмножеством вершин. Тогда:
| \ | | |V MVC MIVS
,
или:
| | | | | | .V MVC MIVS
Таким образом, из неравенств и следует, что:
| | | | | |.V MVC MIVS
Следовательно,
\V MIVS
является минимальным вершинным покрытием, а
\V MVC
является максимальным независимым подмножеством вершин.
В следующей теореме будет установлена эквивалентность задач нахождения
максимального паросочетания и минимального реберного покрытия.
Теорема 3. Для любого графа
( , )G V E
выполняется равенство:
5

Мирзаянов М.Р. Паросочетания и смежные задачи
| ( ) | | ( ) | | |MM G MEC G V
.
Доказательство. Докажем два неравенства.
1. Рассмотрим некоторое максимальное паросочетание
MM
. Очевидно, что оно насыщает
2 | |MM
вершин, и не насыщает
| | 2 | |V MM
. Каждая из ненасыщенных вершин смежна
только с насыщенными вершинами, так как в противном случае паросочетание
MM
можно было бы дополнить соответствующим ребром. Если к множеству
MM
добавить
| | 2 | |V MM
ребер так, что каждое из добавленных ребер инцидентно своей
ненасыщенной вершине, то получившееся множество будет некоторым реберным
покрытием. В этом множестве будет
| | (| | 2 | |)MM V MM
| | | |V MM
ребер. То есть
| | | | | | .MEC V MM
2. Пусть
MEC
– некоторое минимальное реберное покрытие. Рассмотрим граф
( , )T V MEC
. Очевидно, что
T
не содержит циклов, то есть
T
– лес (более того, можно
показать, что каждое дерево в
T
имеет диаметр не более 2). Так как в любом дереве
количество вершин на единицу больше количества ребер, то:
| | | |MEC V K
,
где
K
– количество компонент связности графа
T
.
Cконструируем множество
*
M
, выбрав из каждого дерева графа
T
по одному ребру.
Очевидно, что
*
M
является паросочетанием и
*
| |M K
. Так как
*
| | | |M MM
, то
| | | | | | .MEC V MM
Из неравенств и следует, что
| | | | | |MM MEC V
.
Из конструктивного доказательства теоремы 3 непосредственно следуют алгоритмы
построения максимального паросочетания по минимальному реберному покрытию и
наоборот.
6

Мирзаянов М.Р. Паросочетания и смежные задачи
§4. Эквивалентность задач: MM и MVC для двудольных графов
Теорема 4 (матричная теорема Кенига). Наименьшее количество вертикальных и/или
горизонтальных линий, содержащее все единицы некоторой 0-1 прямоугольной матрицы
равно наибольшему количеству попарно независимых единиц.
В теореме 4 подразумевается, что две единицы 0-1 прямоугольной матрицы независимы,
если они не находятся на одной вертикали и/или горизонтали.
Теорему 4 мы докажем чуть позже.
Поставим в соответствие прямоугольной матрице двудольный граф, вершинами первой
доли которого являются строки данной матрицы, а вершинами второй – столбцы. Каждая
единица матрицы порождает одно ребро в графе, концами которого являются строка и
столбец, на пересечении которых она расположена. Таким образом, наименьшее
количество вертикальных и горизонтальных линий, содержащих все единицы матрицы,
соответствует наименьшему вершинному покрытию в построенном графе. В свою очередь
наибольшее количество попарно независимых единиц соответствует максимальному
паросочетанию. Переформулируем теорему в терминах теории графов.
Теорема 5. В произвольном двудольном графе мощность минимального вершинного
покрытия равна мощности наибольшего паросочетания.
Доказательство теоремы 5 будет приведено позже.
Представим, что нам известно не только доказательство теоремы 5, но и способ перехода
от минимального вершинного покрытия к максимальному паросочетанию (и наоборот).
На рис. 5 показана эквивалентность всех четырех основных задач.
Переход 1-2 осуществляется в силу теоремы 3, 3-4 – в силу теоремы 2, 1-4 – в силу
теоремы 5.
7
Мирзаянов М.Р. Паросочетания и смежные задачи
§5. Построение максимального паросочетания в двудольном графе
Рассмотрим некоторый граф
( , )G V E
. Пусть
M E
– паросочетание в нем.
Цепью будем называть последовательность ребер
P
вида
0 1 1 2 1
( , )( , )...( , )
k k
v v v v v v
. Число
k
называется длиной цепи
P
. Иногда цепи будем записывать в сжатом виде, например,
0 1
, ,...,
k
P v v v
.
Назовем цепь
P
чередующейся относительно паросочетания
M
(или
M
-чередующейся),
если ребра в последовательности поочередно принадлежат
M
и
\E M
.
M
-чередующаяся цепь называется увеличивающей относительно паросочетания
M
, если
ее начальная и конечная вершины ненасыщенны.
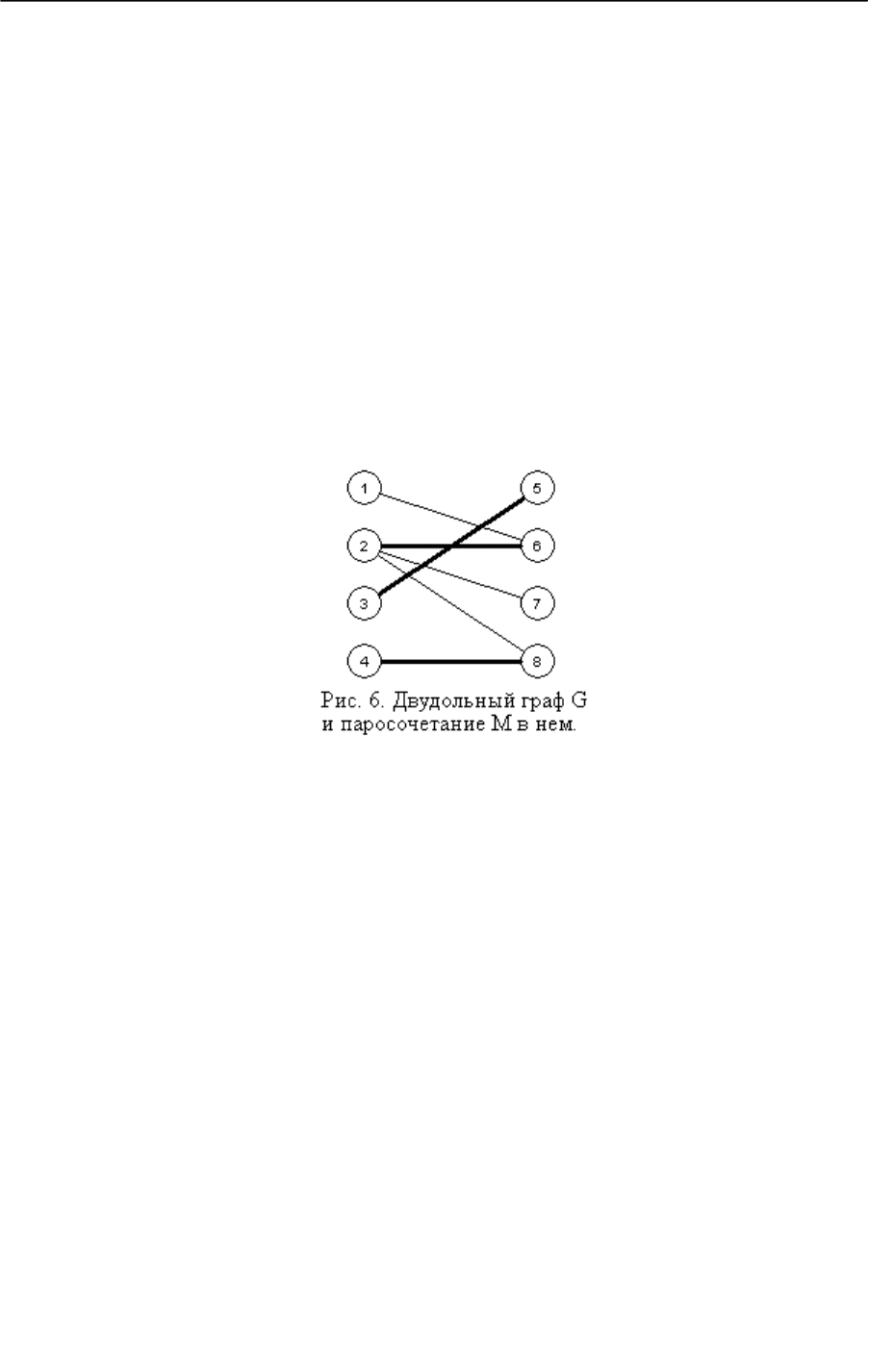
На рис. 6 изображен некоторый двудольный граф
( , , )G X Y E
, выделенные ребра
обозначают ребра паросочетания
M
. Заметим, что для введеных определений граф
G
не
обязательно должен быть двудольным. Перечислим некоторые
M
-чередующиеся цепи в
нем:
4,8, 2,6,1
;
3,5
;
6,2,8, 4
;
1,6,2,7
. Заметим, что последняя из них является
M
-
увеличивающей.
Символом
будем пользоваться для обозначения бинарного оператора симметрической
разности, т.е. если
,A B
– некоторые множества, то
( / ) ( / )A B A B B A
.
Лемма 1. Пусть
( , )G V E
– произвольный неориентированный граф и
M E
–
паросочетание в нем. Тогда если существует
M
-увеличивающая цепь
P
, то
M P
–
паросочетание в
G
и
| | | |M P M
.
Доказательство. В самом деле, так как
P
является
M
-увеличивающей цепью, то ребра
0 1
( , )v v
и
1
( , )
k k
v v
не принадлежат
M
. Следовательно,
P
имеет нечетную длину. Таким
образом,
M P
содержит на одно ребро больше, чем
M
.
8

Мирзаянов М.Р. Паросочетания и смежные задачи
Покажем, что
M P
является паросочетанием. Предположим, что некоторая вершина
v
V
инцидентна более чем одному ребру из
M P
. Так как вершины
0
,
k
v v
–
ненасыщенны паросочетанием
M
, то
0
v v
и
k
v v
. Значит вершина
v
является
внутренней вершиной цепи
P
. Из тех ребер множества
M P
, которые инцидентны
v
ровно одно принадлежит
P
, и не менее одного принадлежит
\M P
. Так как
P
является
M
-чередующейся цепью, то существует некоторое ребро из
M P
инцидентное
v
.
Таким образом в
M
существует два ребра
1
\e M P
и
2
e M P
инцидентных
v
, чего
не может быть.
Следующая теорема является ключевой для большинства алгоритмов нахождения
максимальных паросочетаний.
Теорема 6 (Берж, [2]). Паросочетание
M E
неориентированного графа
( , )G V E
максимально тогда и только тогда, когда не существует
M
-увеличивающих цепей.
Доказательство. Из леммы 1 непосредственно следует необходимость отсутствия
M
-
увеличивающих цепей.
Докажем достаточность. Пусть
M
такое паросочетание в
( , )G V E
, для которого не
существует
M
-увеличивающих цепей. Предположим существует максимальное
паросочетание
*
M
, такое что
*
| | | |M M
. Рассмотрим граф
*
( , )H V M M
. Очевидно,
что степень каждой вершины в
H
не более 2, то есть граф
H
является объединением
непересекающихся цепей и циклов. Заметим, что любые два ребра графа
H
инцидентных
одной вершине таковы, что одно из них принадлежит
M
, а другое –
*
M
, следовательно,
все циклы в графе
H
– четные. Все цепи в
H
имеют четную длину, так как в противном
случае они образовывали бы либо
M
-увеличивающие цепи, либо
*
M
-увеличивающие
цепи в графе
G
. Таким образом, в графе
H
содержится равное количество ребер из
паросочетания
M
и из паросочетания
*
M
. Тогда
*
*
| |
| | | |
2
M M
M M M
, но
*
| |M
равна этой же величине, следовательно,
*
| | | |M M
, что противоречит предположению
*
| | | |M M
.
Из теоремы 6 непосредственно следует метод нахождения максимального паросочетания.
9
Мирзаянов М.Р. Паросочетания и смежные задачи
Алгоритм 1
Вход: неориентированный граф
( , )G V E
и паросочетание
M E
(возможно
M
)
Выход: максимальное паросочетание
max
M
Метод:
01 while существует
M
-удлиняющая цепь do
02 построить такую цепь
P
03
:M M P
04
max
:M M
Заметим, что алгоритм 1 не является в некотором смысле алгоритмом, так как в нем не
детализируется способ нахождения
M
-удлиняющей цепи. Так же важно отметить, что до
настоящего момента мы рассматривали не обязательно двудольные графы и алгоритм 1
верен для графов в общем случае.
Ниже будет считать, что граф
( , , )G X Y E
является двудольным. Построим новый
ориентированный граф
( , )
M
H X Y E
. Множество ориентированных ребер
M
E
составлено из ребер множества
\E M
ориентированных от доли
X
к доли
Y
и ребер
множества
M
ориентированных от
Y
к
X
.
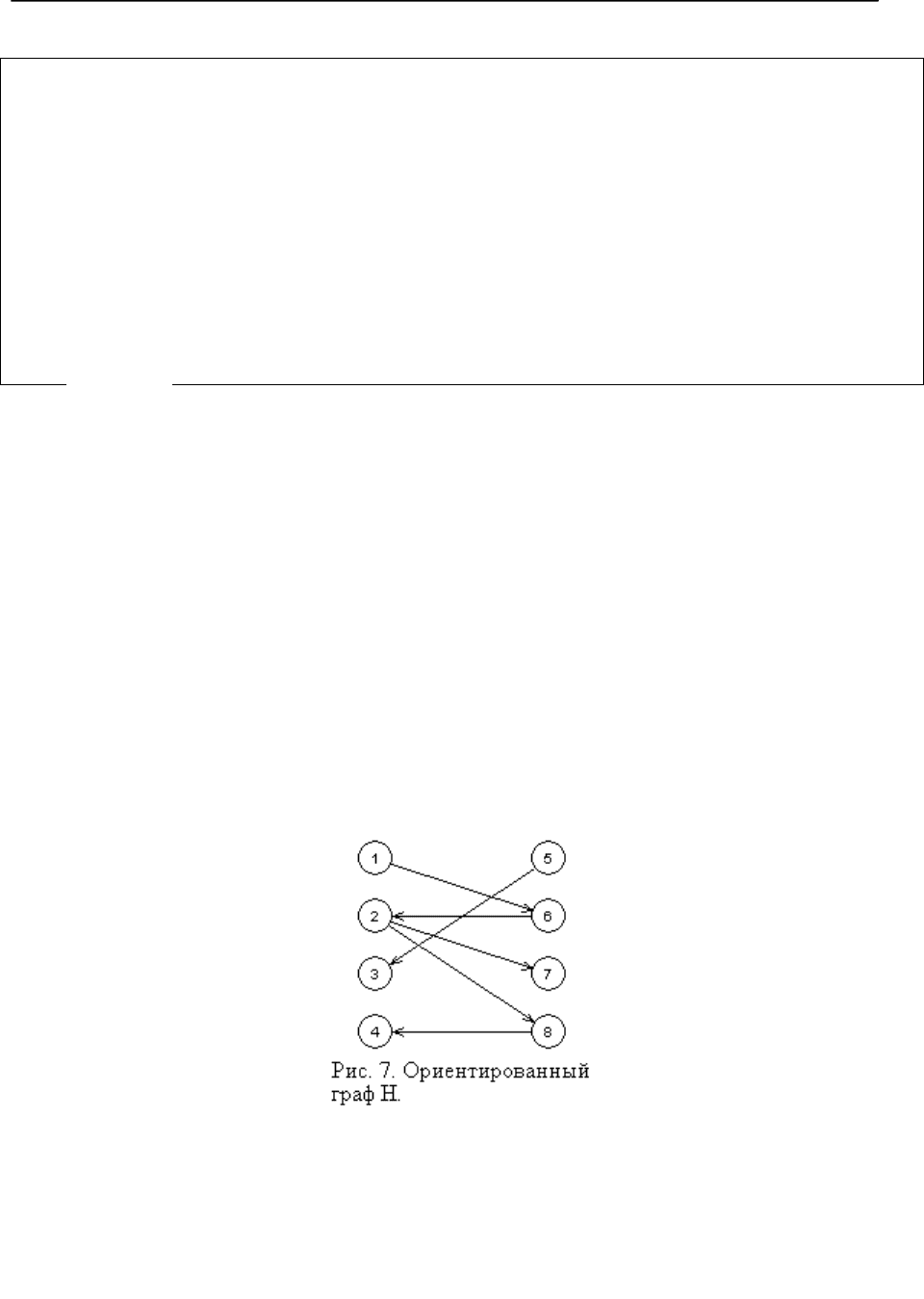
На рис. 7 изображен соответствующий ориентированный граф
H
, соответствующий
двудольному графу на рис. 6.
Очевидно следующее утверждение.
Утверждение 1. Если в орграфе
H
существует ориентированная цепь из ненасыщенной
вершины доли
X
в ненасыщенную вершину доли
Y
, то такой путь в графе
G
образует
M
-удлиняющую цепь.
10
