Минченко Л.И. Краткий курс численного анализа
Подождите немного. Документ загружается.

,1 , 1, , 1,
22
(2 )
1
0
2
ij ij i j ij i j
Uu U UU
hh
++−
−−+
−=
откуда
,1 1, 1,
2
11
22
0
ij i j i j
UUU
h
++ −
−−
=
.
Граничные условия будут иметь вид
.,0ii
Ug=
,
,oj j
U
ϕ
=
,
,nj j
U
ψ
=
,
где ,
)(
ii
xgg =
)(
jj
t
ϕ
ϕ
=
,
)(
jj
t
ψ
ψ
=
.
Таким образом, мы имеем разностную схему
)()( hh
h
fUL =
,
где
, 1 1, 1,
2
()
,0
0,
,
11
22
(, ),
0,
0,
0, ,
ij i j i j
h
h
i
j
nj
UUU
для ij соответствующих внутренним узлам
h
LU
U при in
U при jm
u при jm
++ −
⎧
−−
⎪
⎪
⎪
⎪
=
⎨
=
⎪
=
⎪
⎪
=
⎪
⎩
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=
=
=
=
.,0,
,0,
,0,
),,(,0
)(
mj
mj
nig
сеткиузламвнутреннимующихсоответствjiдля
f
j
j
i
h
ψ
ϕ
Покажем, что разностная схема сходится на решении
дифференциальной краевой задачи.
(,)Uxt
Порядок аппроксимации определить легко. Точность разностной
аппроксимации производной
t
U
∂
∂
определяется , производной )()(
2
hOlO =
2
2
x
U
∂
∂
− , граничные условия аппроксимируются точно. В итоге, разностная
схема имеет порядок аппроксимации .
)(
2
hO
)(
2
hO
Покажем, что построенная разностная схема устойчива. Рассмотрим
возмущенную краевую задачу
)()( hh
h
fzL =
с произвольной правой частью
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=
=
=
=
,,0,
,0,
,0,
),(,
)(
mj
mj
nig
Dузламвнутреннимующихсоответствjiвсехдляf
f
j
j
i
hij
h
ψ
ϕ
131
где ,
ij
f
i
g
,
j
ϕ
,
j
ψ
− произвольные сеточные функции, определенные на
внутренних и граничных узлах сетки.
Надо показать, что возмущенная задача имеет
1) единственное решение ;
)( h
z
2) это решение удовлетворяет оценке
hh
F
h
U
h
fCz
)()(
≤
, (12.23)
где
ij
ji
U
h
zz
h
,
)(
max=
,
}max,max,max,maxmax{
,
)(
ij
ji
j
j
j
j
i
i
F
h
fgf
h
ψϕ
=
.
Существование решения и его единственность вытекают из того, что
значения на нулевом слое (при
)( h
z
0
=
j
) определяются граничными
условиями, в первом слое (
1
=
j
) однозначно определяются из разностной
схемы и т.д.
С другой стороны
nifgz
h
i
i
,0,
)(
0,
=≤≤ .
Далее
.,0,
2
1
2
1
2
1
2
1
1
2)(
1
2
1
2
0,10,11,
nifhffhggfhzzz
i
h
i
ii
iiii
=+≤++≤++≤
−+
Отсюда
nifhz
h
i
,0,)1(
)(2
1,
=+≤
.
Аналогично
nifhfhfhz
h
i
h
i
,0,)21()1(
)(2
2,
2)(2
2,
=+≤++≤
,
… … … … … … … … … … … … … … … …
nifmhz
h
mi
,0,)1(
)(2
,
=+≤
.
Поскольку
constTa
h
hTa
h
l
T
mh ==
⋅⋅
==
2
2
22
22
2
2
,
то
)()( hh
fCz ≤
.
Таким образом, разностная схема устойчива и, следовательно, в силу
теоремы 1 она сходится на решении дифференциальной краевой
задачи с порядком сходимости .
(,)Uxt
)(
2
hO
132
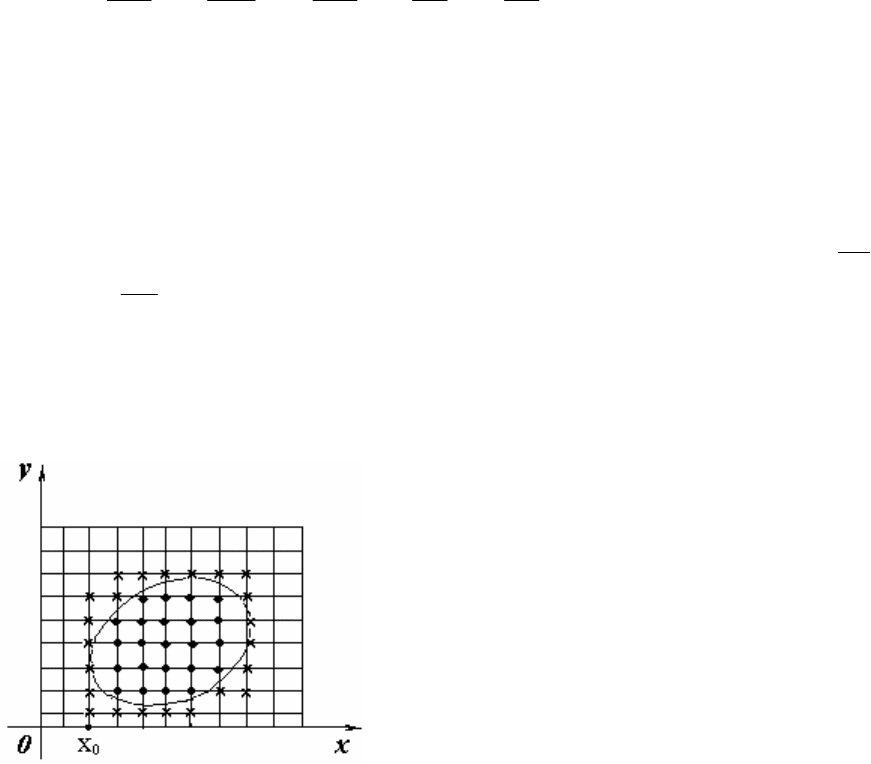
13. СВОЙСТВА РАЗНОСТНЫХ СХЕМ ДЛЯ УРАВНЕНИЙ С
ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Пусть − область на плоскости , ограниченная контуром Γ . Рассмотрим
дифференциальную краевую задачу
D
xy0
fLU =
, (13.1)
где
⎪
⎪
⎩
⎪
⎪
⎨
⎧
Γ∈
∈+
∂
∂
+
∂
∂
+
∂
∂
+
∂∂
∂
+
∂
∂
=
Γ
,),(|
),(
332313
2
2
22
2
12
2
2
11
yxприU
DyxприUa
y
U
a
x
U
a
y
U
a
yx
U
a
x
U
a
LU
⎪
⎩
⎪
⎨
⎧
Γ∈
∈
=
,),(),(
),(),(
yxприyx
Dyxприyxg
f
ϕ
),( yxUU =
− неизвестная функция двух переменных.
Разобьем область с помощью прямых
D niihxx
i
,0
0
=+= ,
mjjlyy
j
,0
0
=+= . Каждый узел , лежащий внутри области, будем
называть внутренним и множество внутренних узлов обозначим . Узлы,
лежащие на контуре (если они есть) и узлы, окаймляющие контур
),(
ji
yx
*
D
Γ
Γ
извне,
будем называть граничными и обозначим их совокупность (см. рисунок
13.1).
*
Γ
Рис. 13.1
Обычно выбирают , где
)(hrl =
r
− некоторая функция, или , где
rhl =
r
− постоянная. Совокупность всех узлов обозначают
**
Γ∪= DD
h
и называют сеткой.
Функцию , определенную на сетке , будем называть сеточной. Т.е.
это функция, которая ставит в соответствие каждому узлу число
.
)(h
U
h
D
hji
Dyx ∈),(
ijji
uyxU =),(
Обозначим через пространство всех сеточных функций на сетке и
введем в нем норму сеточной функции , положим
h
U
h
D
)(h
U
133

)(
,
)(
max
h
ij
ji
U
h
uU
h
=
,
где максимум берется по всем узлам сетки .
h
D
Построим для дифференциальной краевой задачи (13.1) разностную
схему
)()( hh
h
fUL =
, (13.2)
определенную на сетке , где
h
D
⎪
⎪
⎩
⎪
⎪
⎨
⎧
Γ∈
∈=
Γ
,),(,|
),(),1(
,
*)(
*)(
*
ji
h
ji
h
h
yxприU
Dyxприизуравненияальногодифференци
частилевойующаясоответствсхемаРазностная
UL
⎪
⎩
⎪
⎨
⎧
Γ∈
∈=
=
,),(,
),(),,(
**
*
)(
jiij
jijiij
h
yxпри
Dyxприyxgg
f
ϕ
где − значение функции
*
ij
ϕ
),( yx
ϕ
в точке на контуре , ближайшей к узлу
.
Γ
*
),( Γ∈
ji
yx
Будем предполагать далее, что
1) дифференциальная краевая задача (13.1) имеет решение
, причем единственное;
),( yxUU =
2) разностная краевая задача (13.2) имеет единственное решение
при любом выборе шага
h
меньшего некоторого значения .
0
h
Определим сеточную функцию , значения которой совпадают на
сетке со значениями решения дифференциальной краевой задачи
(13.1) в узлах сетки .
h
U ][
h
D
),( yxU
h
D
Определение 1. Будем говорить, что разностная схема (13.2) сходится на
решении дифференциальной краевой задачи (13.1), если
),( yxU
0][
)(
→−
h
U
h
h
UU
при ,
0→h
где − решение разностной краевой задачи (2). При этом, если
)(h
U
m
U
h
h
hCUU
h
1
)(
][ ≤−
,
где не зависящая от , то имеет место порядок сходимости .
constC =
1
h
)(
m
hO
Введем пространство сеточных функций , элементами которого
являются всевозможные сеточные функции , определенные на сетке .
Норму в пространстве определим как
h
F
)(h
f
h
D
h
F
**
),(),(
)(
maxmax
Dyx
ij
yx
ij
F
h
jiji
h
gf
∈Γ∈
+=
ϕ
.
Введем невязку
)()(
][
h
hh
h
fULf −=
δ
,
соответствующую решению
),( yxUU
=
дифференциальной краевой задачи
(13.1).
134
Определение 2. будем говорить, что разностная схема (13.2)
аппроксимирует дифференциальную краевую задачу (13.1) на ее решении
, если
),( yxUU =
0
)(
→
h
F
h
f
δ
при .
0→h
При этом будем говорить, что имеет место порядок аппроксимации ,
если
)(
m
hO
m
F
h
hCf
h
2
)(
≤
δ
,
где не зависит от .
constC =
2
h
По аналогии с §12 введем понятие устойчивости разностной схемы.
(Отметим, что в данном параграфе мы имеем дело с линейными
дифференциальными операторами ).
LU
Определение 3
. Разностная схема (13.2) называется устойчивой, если
существует число такое, что для любого
0
0
>h
0
hh
<
разностная краевая
задача (2) имеет единственное решение при любой правой части , и это
условие удовлетворяет условию
)(h
f
)()( hh
fCU ≤ ,
где не зависит от
h
и .
constC =
)(h
f
Теорема 1. Пусть разностная схема (13.2) аппроксимирует
дифференциальную краевую задачу (13.1) с порядком аппроксимации
и разностная схема (13.2) устойчива. Тогда разностная схема (13.2) сходится
на решении дифференциальной краевой задачи (13.1) с порядком
сходимости .
)(
m
hO
),( yxU
)(
m
hO
Пример. Рассмотрим задачу теплопроводности
0
2
2
2
=
∂
∂
−
∂
∂
x
U
a
t
U
, ,
],[ Lox ∈ ],0[ Tt
∈
,
с граничными условиями
)()0,( xgxU =
,
)(),0( ttU
ϕ
=
,
)(),( ttLU
ψ
=
.
Введем сетку , определенную прямыми
h
D
niihx
i
,0, == ; mjjlt
j
,0, == ,
где
2
2
2
,/,/
a
h
llTmhLn ===
.
Составим разностную схему, соответствующую рассматриваемой
дифференциальной краевой задаче в узлах сетки . Получим
h
D
0
),(),(2),(),(),(
2
11
2
1
=
+
−
−
−
−++
h
txutxutxu
a
l
txutxu
jijijijiji
или, полагая ,
),(
, jiji
txuu =
0
)2(
2
1
2
,1,,1
2
,1,
=
+
−
−
−
−++
h
uuu
h
uu
jijijijiji
откуда
135

0
2
1
2
1
2
,1,11,
=
−−
−++
h
uuu
jijiji
.
Граничные условия будут иметь вид
ii
gu =
0.,
,
jjo
u
ϕ
=
,
,
jjn
u
ψ
=
,
,
где ,
)(
ii
xgg =
)(
jj
t
ϕ
ϕ
=
,
)(
jj
t
ψ
ψ
=
.
Таким образом, мы имеем разностную схему
)()( hh
h
fUL =
,
где
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
=
=
=
−−
=
−++
,,0
,0
,0
),,(
2
1
2
1
,
,0
0,
2
,1,11,
)(
mjприu
mjприu
niприu
узламвнутреннимующихсоответствjiдля
h
uuu
UL
jn
j
i
jijiji
h
h
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=
=
=
=
.,0,
,0,
,0,
),,(,0
)(
mj
mj
nig
сеткиузламвнутреннимующихсоответствjiдля
f
j
j
i
h
ψ
ϕ
Покажем, что разностная схема сходится на решении
дифференциальной краевой задачи.
),( txu
Порядок аппроксимации определить легко. Точность разностной
аппроксимации производной
t
U
∂
∂
определяется , производной )()(
2
hOlO =
2
2
x
U
∂
∂
− , граничные условия аппроксимируются точно. В итоге, разностная
схема имеет порядок аппроксимации .
)(
2
hO
)(
2
hO
Покажем, что построенная разностная схема устойчива. Рассмотрим
возмущенную краевую задачу
)()( hh
h
fzL =
с произвольной правой частью
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=
=
=
=
,,0,
,0,
,0,
),(,
)(
mj
mj
nig
Dузламвнутреннимующихсоответствjiвсехдляf
f
j
j
i
hij
h
ψ
ϕ
где ,
ij
f
i
g
,
j
ϕ
,
j
ψ
− произвольные сеточные функции, определенные на
внутренних и граничных узлах сетки.
Надо доказать, что возмущенная задача имеет
3) единственное решение ;
)(h
z
136
4) это решение удовлетворяет оценке
hh
F
h
U
h
fCz
)()(
≤
,
где
ij
ji
U
h
zz
h
,
)(
max=
,
}max,max,max,maxmax{
,
)(
ij
ji
j
j
j
j
i
i
F
h
fgf
h
ψϕ
=
.
Существование решения и его единственность вытекают из того, что
значения на нулевом слое (при
)(h
z
0
=
j
) определяются граничными
условиями, в первом слое (
1
=
j
) однозначно определяются из разностной
схемы и т.д.
С другой стороны
nifgz
h
i
i
,0,
)(
0,
=≤≤ .
Далее
.,0,
2
1
2
1
2
1
2
1
1
2)(
1
2
1
2
0,10,11,
nifhffhggfhzzz
i
h
i
ii
iiii
=+≤++≤++≤
−+
Отсюда
nifhz
h
i
,0,)1(
)(2
1,
=+≤
.
Аналогично
nifhfhfhz
h
i
h
i
,0,)21()1(
)(2
2,
2)(2
2,
=+≤++≤
,
… … … … … … … … … … … … … … … …
nifmhz
h
mi
,0,)1(
)(2
,
=+≤
.
Поскольку
constTa
h
hTa
h
l
T
mh ==
⋅⋅
==
2
2
22
22
2
2
, то
)()( hh
fCz ≤ .
Таким образом, разностная схема устойчива и, следовательно, в силу
теоремы 1 она сходится на решении дифференциальной краевой задачи
с порядком сходимости .
),( txu
)(
2
hO
137
ЛИТЕРАТУРА
1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М:
БИНОМ, 2004. – 636с.
2. Мысовских И.П. Лекции по методам вычислений. М.: Наука, 1993. –
496с.
3. Калитин Н.Н. Численные методы. – М : Наука, 1978. – 612с.
4. Бахвалов Н.С. Численные методы. – М : Наука, 1976. – 632с.
5. Демидович В.П. и др. Численные методы анализа. –М: Физматгиз,
1963. – 400с.
6. Волков Е.А. Численные методы. – М: Наука, 1982. – 255с.
7. Крылов В.И. и др. Вычислительные методы высшей математики. Т.1.
- Мн : Выш шк., 1972. – 684с.
8. Крылов В.И. и др. Вычислительные методы высшей математики. Т.2. –
Мн : Выш. шк., 1976. – 672с.
9. Форсайт Дж. и др. Машинные методы математических вычислений. –
М : Мир, 1980. – 280с.
10. Шуп Т. Решение инженерных задач на ЭВМ. – М: Мир, 1982. – 238с.
11. Сборник задач по методам вычислений / Под ред. Монастырного П.И.
– М: Наука, 1994. – 318с.
12. Самарский А.А. Введение в численные методы. – М: Наука, 1987. –
288с.
13. Березин И.С. , Жидков Н.П. Методы вычислений. Т.1. - М: Фитматгиз,
1962. – 464с.
138

Св. план 2005,поз.52
Учебное издание
Минченко Леонид Иванович
КРАТКИЙ КУРС ЧИСЛЕННОГО АНАЛИЗА
Учебное пособие по курсу «Методы численного анализа» для
студентов специальности «Информатика» для всех форм
обучения
В 2-х частях
Часть1
Редактор Т.Н.Крюкова
Корректор
Подписано в печать Формат 60х84 1/16 Бумага
Гарнитура «Таймс» Печать офсетная Усл.-печ.л.
Уч.-изд.л. Тираж 150 экз. Заказ
Издатель и полиграфическое исполнение: Учреждение образования «Белорусский
государственный университет информатики и радиоэлектроники»
Лицензия на осуществление издательской деятельности№ 02330/0056964 от 01.04.2004.
Лицензия на осуществление полиграфической деятельности№ 02330/0131518 от 30.04.2004.
220013, Минск, П.Бровки, 6
139
140
