Mayr E.W., Pr?mel H.J., Steger A. (eds.) Lectures on Proof Verification and Approximation Algorithms

Подождите немного. Документ загружается.

184 Chapter 7. Bounds for Approximating MAXLINEQ3-2 and MAxEkSAT

- a set V e (v~v(*)), and

functions ]:B y ~ B and

gl,g2:B W --~ B.

It then reads three bits from ~r:

AY(f),

Br and Br and decides on

the basis of these bits whether or not the test has been successful. The values

r V, f, gl, and g2 are chosen according to one of two distributions, which are

introduced in the following.

Write T for the set of all pairs (r V) where r e (~) and V e (v~v(r and

write fl for the set of all tuples

where (r

e T, f:B v --~ B,

and gl, 92: B v~(r -~ B.

For a set W, a set V C W, and a function y:W -~ B, let

y~V

denote the

restriction of y to V.

Both distributions are distributions over ft. The first distribution, denoted D ~

is determined by the following rules how to pick an element (r V, f, gl, g2) from

fl:

an element (r V) from T is chosen randomly, and W is set to Vat(C),

- for every x: V ~ B, f(x) is chosen randomly,

- for every y: W --~ B,

gl(Y)

is chosen randomly, and

- for every y: W --~ B,

g2(Y)

is set to

.f(y'~V) 9 gl(y)

with probability 1 - 6 and

-f(y'tV) 9

gz(y) with probability 6.

The other distribution, denoted D6, is determined in a similar way:

an element (r V) from T is chosen randomly, and W is set to Vat(C),

for every x: V -+ B, f(x) is chosen randomly,

- for every y: W ~ B,

gl(Y)

is chosen randomly,

- for every y: W ~ B,

.f(y'~Y)

= 1, then g2(Y) is set to

-gl(Y), and

- if

f(y'tV)

= -1, then

g2(Y)

is set to -gl (Y) with probability 6 and to gl(Y)

with probability 1 - 6.

Observe that in both definitions we could have expressed gl(Y) in terms of g2 (Y)

just in the same way we expressed g2 (y) in terms of gl (Y), i.e., the distributions

are symmetric with respect to gl and g2.

We will write Prob~ respectively Prob# for the corresponding probability func-

tions.

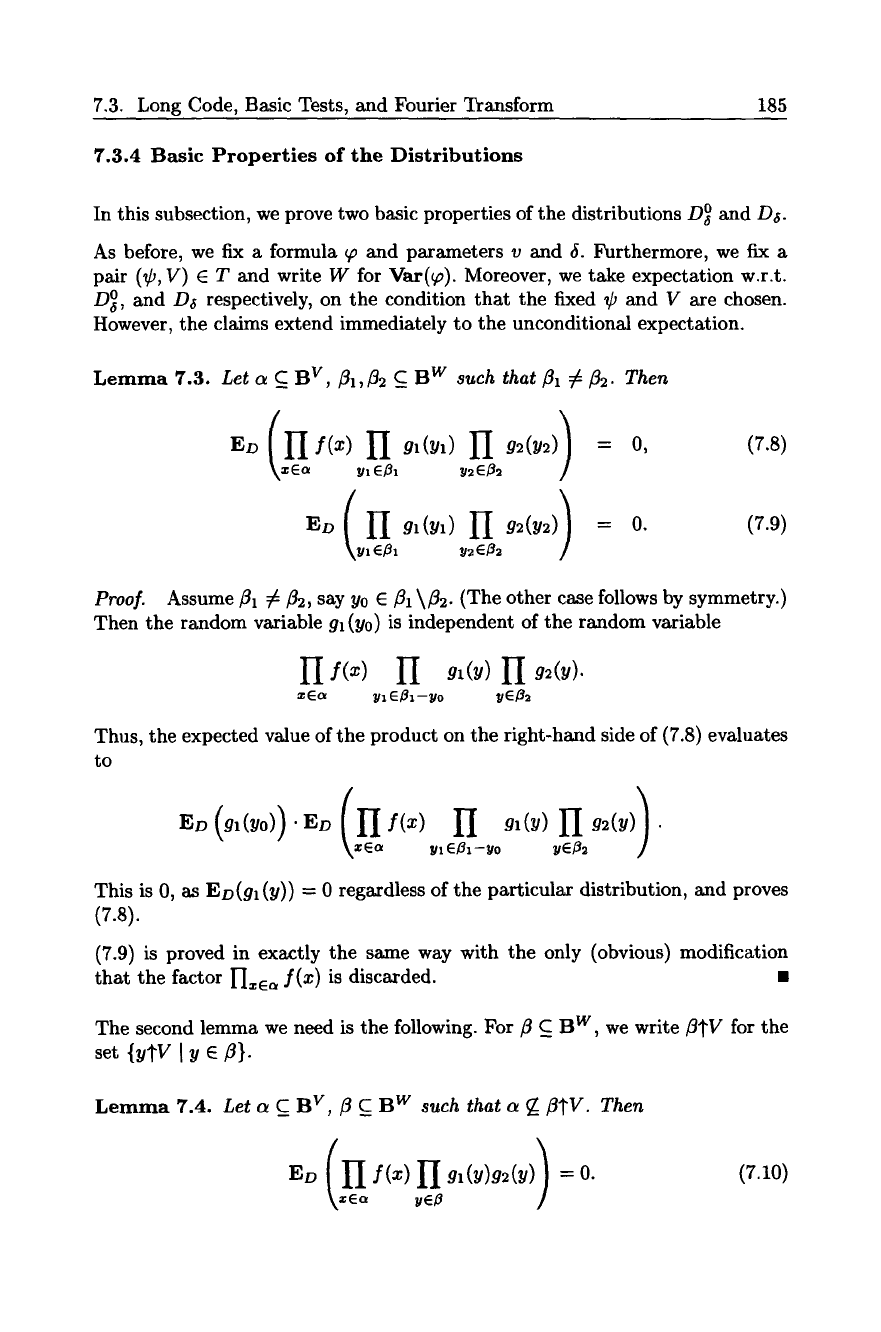
7.3. Long Code, Basic Tests, and Fourier Transform 185

7.3.4 Basic Properties of the Distributions

In this subsection, we prove two basic properties of the distributions D~ and D~.

As before, we fix a formula qo and parameters v and 6. Furthermore, we fix a

pair (r V) E T and write W for Vat(to). Moreover, we take expectation w.r.t.

D ~ and D~ respectively, on the condition that the fixed r and V are chosen.

However, the claims extend immediately to the unconditional expectation.

Lemma 7.3.

Let a C_ B v, 131, ~2 C B w such that fllr f12. Then

ED ( n gl(~]l) H g2(Y2)) ~" 1 y2E82

(7.s)

(7.9)

Pro@

Assume

f~l ~ ~2, say Y0 E f~l \~2.

(The other case follows by symmetry.)

Then the random variable gl(Y0) is independent of the random variable

f(x) H gl(y) H

x Ga yl EI31--yo yEB2

Thus, the expected value of the product on the right-hand side of (7.8) evaluates

This is 0, as ED(gl (y)) = 0 regardless of the particular distribution, and proves

(7.8).

(7.9) is proved in exactly the same way with the only (obvious) modification

that the factor 1-Ixe~ f(x) is discarded. 9

The second lemma we need is the following. For fl C B W, we write/3~V for the

set

{y'rV [ y E ~}.

Lemma 7.4.

Let a C_ B V, fl C B W such that a ~ fl~V. Then

(7.1o)

186 Chapter 7. Bounds for Approximating MAXLINEQ3-2 and MAXEkSAT

Proof.

The proof has the same pattern as the, previous one with the only dif-

ference that here

f(xo)

and

fix)

H gl(Y)g2(Y)

xGo~--zo yE/~

are independent random variables for an element

xo E a \ fltV.

7.3.5 Fourier Transforms

From an algebraic point of view (see, e.g., [LMN93]), Fourier transforms are

particular linear transformations on certain vector spaces. We will use Fourier

transforms as the major mathematical (combinatorial) tool for the analysis of

the verifiers to be constructed in the proofs of Theorems 7.1 and 7.2. In this

subsection, we first develop the notion of a Fourier transform (which the reader

already familiar with Fourier transforms can skip) and then give some lemmas

about Fourier transforms we will use later.

Let M be a finite set of cardinality m. We are interested in functions defined on

B M with values in B.

Assume fl and f2 are functions M -~ B. If fl = f~, then

H fi( )f2(x) = 2

fl(x0)f2(x0) H fl(x)f2(x)

aCM-xo x~a

aC_M xfic~

On the other hand, if f: # f2, say

f:(xo) #

f2(x0), then

H fl(X)f2 (X)

olCM xEct

= E

o~C_M-zo z6a

~C_M-xo

That is,

2 m, iff:=A,

~-, H f:(x)f2(x)---

if fl # f2-

aCM xEo~

So, for each function A: B M --+ B and f: M ~ B,

A(f) = Z 2-mA(f') ~ H f(x)f'(x)

I':M--+B aC_M zEa

a~CM( 2-m Z

A(f')Hf'(x)l Hf(z)"

-- f':M-'tB xEex ] xEvt

7.3. Long Code, Basic Tests, and Fourier Transform 187

Setting

we can thus write:

Ja = 2 -m Z A(f) H f(x),

(7.12)

I:M--c'B z6ol

a(s) = ~ ~. H/(x)" (7.13)

aCM xGa

Observe the duality between (7.12) and (7.13). The real numbers -4a are called

the Fourier coefficients of A. They can as well be viewed as expectations (where

we assume a uniform distribution on the set of all f: M --+ B):

Lemma 7.5 (Parseval's identity).

Let A: B M -+ B be an arbitrary ]unction.

Then

}2 ~=1.

~C__M

Proof.

By definition,

aC M - f ,f' :M-+ B zEc~ ]

which, by (7.11), evaluates to 1.

Lemma 7.6.

Let A: B M --4 B be a ]unction such that A(-f) = -A(f). Assume

that a C_ M has even cardinality. Then Aa = O.

Proof.

By definition,

= 2-m $: A(:)II :(x).

f:M-'-~B zEa

Fix an arbitrary element from M, say x0. Splitting the right-hand side of the

above equation according to whether

f(xo) = 1 and f(xo)

= -1 leads to

\f: ,1(

o)---- xea f:M--~B,f(xo)=-I

which is the same as

2-m Z

f:M---~.B,f(zo)=l

188 Chapter 7. Bounds for Approximating MAXLINEQ3-2 and MAXEkSAT

which, in turn, by assumption that a has an even number of elements, is identical

with

I:M-~B,I(xo)=I

zGa zEa

Clearly, the last expression is 0. 9

Lemma 7.7.

Let B be a ]unction B M --r B and assume h: M --+ B is such that

B(g) = B(max(g, h))

for all g: M -+ B. Furthermore, let/5 C_ M be such that

B B # O. Then h(y) = -1 for all y E/3.

Proof.

The proof goes by way of contradiction. Assume

h(yo)

-- 1 for some

Y0 E/~. By definition and assumption,

/3B = 2-m Z

B(max(g,h)) H g(x).

g:M--+B YGB

Just as in the proof of the previous lemma, we split the sum on the right-hand

side and obtain for/3B:

2 -m ( ~ B(max(g, h)) n

g(Y) +

g: M---~B,g(yo ) = 1 FeB

B(max(g,h)) IXeBg(y)).

g: M--c B,g( yo )=-- I

For every function g, let g' denote the function obtained from g by modifying g

to take the value

-g(Yo)

at Y0. The previous expression can then be written as

2-m Z (B(max(g,h)) H g(Y) + B(max(g',h)) H g'(y)l .

g:M-~B,g(yo)=l FeB FeB /

Since h(yo) = 1, we know max(g, h) = max(g', h). Thus the previous expression

is identical with

2-m Z

g:M-*B,g(vo)----1

B(max(g,h)'(IIg(Y'+IIg'(Y) ) 9

\veB FeB

Now observe that by definition of g', the last term can also be written as

2-m X B(max(g,h)) (Hg(y) - H g(Y)l '

g:M--~B,g(yo)=l yEB yEB ]

which is O. 9

7.4. Using the Parallel Repetition Theorem for Showing Satisfiability

'/.4

Using the Parallel

Repetition Theorem for Showing

Satisfiability

189

The application of the weak version of the Parallel Repetition Theorem 6.4 in

the proofs of the main theorems of this chapter will be via the following lemma.

There, we use the feature of E-RoBE3SAT-b that each variable in the given

formula ~o occurs at most b times for some constant b 9 N. This implies that for

large I~1 the probability of choosing non-disjoint clauses tends to zero. Let

re(v)

be s.t. Iqol >/re(v) implies that this probability is at most 1/2.

Lemma 7.8.

For any small

6,6',7 > 0,

and for any k E N, there exists a

constant v(6, 6',7, k) e N such that for all v >1 v(6,6',7, k), and for all instances

qa of e-ROBE3SAT-b of

length

I~1/> re(v)

the following holds.

Assume that there exists a proof

rr = . ((AV)ve(v,,~,)), (Br162 .

for the for-

mula ~o such that

I( )'

a: lal~<k a: Io, l~<k,ana,laVl>j~

where ~ lq 13 may be any condition that implies the existence of some y 9 13 such

that (y'fV) 9 a, and the expectation is taken w.r.t, the distribution of (r V)

according to D~, or DO,.

Then 99 is satisfiable.

Strictly speaking, the Weak Parallel Repetition Theorem is used only as a tech-

nical tool for proving the above lemma, and one can at least in principle imagine

that the lemma can also be proven without using the theorem. But one should

note that the probabilistically checkable proofs as introduced in the last section

are just made in such a way that they are in a close relation to the parallel

repetition of a certain MIP-protocol.

The pivotal point in the claimed correspondence is the choice of v clauses r and

v formulae V performed by the verifiers. Under both distributions D6 and D ~

this random choice corresponds essentially to the v-fold parallel repetition of the

MIP(2,1)-protocol 6.2 where r is given to the first prover and V to the second.

That this correspondence is an only "essential", not "exact" one is due to the

case of non-disjoint clauses r which is unavoidable in the parallel repetition of

Protocol 6.2 but excluded in the Distributions D~ and D 0.

To overcome this difficulty we made the assumption that I~ol >/

re(v)

which

implies that the case of non-disjoint clauses occurs with probability at most 1/2.

This bound will be used in the proof of the temma below in that we may restrict

190 Chapter 7. Bounds for Approximating MAXLINEQ3-2 and MAxEkSAT

to the case of disjoint clauses only, without reducing the success rate of the

provers by more than a factor of 2.

In case of disjoint clauses, we may see a probabilistically checkable proof ~r =

(CA)v~(V,r(~)), (Br162 as a (deterministic) strategy for the provers if each

A V, B ~

is in fact the long code of an assignment to V, respectively. Var(r The

provers may then just return that assignment to the MIP-verifier. Conversely

each deterministic strategy of giving back certain assignments can be converted

into long codes. Let us point out that this correspondence serves only as an

illustration of what is going on. How to get formally prover strategies from

probabilistically checkable proofs ~r will be described in the course of the proof of

Lemma 7.8 below. The construction given there applies to any proof 7r certifying

a certain expectation as stated in the assumption of the lemma. We will not

need to restrict to case ~r being a long code.

Proof of Lemma 7.8.

We describe a strategy for the provers of Protocol 6.2 to

convince the verifier of the satisfiability of the given formula. We will show that

under the given assumption this strategy will have a success rate greater than

-~- a constant

independent of v.

4k 2 ,

Then we can use the Weak Parallel Repetition Theorem stating that the success

rate in the case of inputs to be rejected will tend to zero with increasing repeti-

tion factor. Hence there exists a constant v0 E N, which we use as the claimed

v(5,5',% k), such that for all v >/vo:

If the v-fold parallel repetition of Protocol 6.2 is performed on an un-

satisfiable ROBE3SAT instance ~, then there do not exist any strategies

for the provers having a success rate greater than 4k-~"

Consequently ~ has to be satisfiable.

To complete the proof it remains to give prover strategies which have a success

rate greater than ~ under the given assumption of the lemma. In advance,

we remind of the fact (Lemma 7.7), that only those Fourier coefficients/~ are

non-zero, where f~ contains only assignments for Vat(C) which satisfy r Since

the strategy of ~rover P1 below returns only assignments which are contained in

some f~ with/~ ~ 0, this guarantees the satisfaction of r Thus, for convincing

the verifier of Protocol 6.2, the prover strategies need only return with sufficient

probability a pair of assignments (x, y) s.t.

x = y~V.

We will call a pair (x, y)

compatible

iff

x = y~V.

In the following, we consider the situation that some fixed r V are given to the

provers. We use as abbreviation W = Var(r and we omit superscripts r V of

B and A, respectively.

PROVERSTRATEGY If the chosen clauses have non-disjoint sets of variables, P1

will give up, and only in this case it may happen that IVI < v, in which case

also P2 has to give up.

7.4. Using the Parallel Repetition Theorem for Showing Satisfiability 191

Otherwise, both provers will base their behavior on the same proof lr as given

by the assumption.

/)1: Choose/3 C BW,)/31 ~< k, with probability proportional /~. Return ran-

domly some y E/3 to the verifier.

O oo e o

,o,

wit ,ro ,,ty .roport on I ol

choose randomly some x E a and return it to the verifier.

Note that not in any case appropriate a and/3 need to exist. If for some V and r

the provers cannot find a respectively./3 which meet the above conditions they

will give up. In the following we will call a and/3

admissible

if they meet the

above conditions. Since the sum in the assumption of the lemma ranges just over

admissible a and/3, there exist admissible a and/3 with a certain probability.

In the following, we consider the case that some r is chosen which has clauses

with disjoint sets of variables i.e., we calculate the probability under the con-

dition of the disjointness of r From this the unconditional probability will be

estimated at the end of the proof.

Let us see what happens if admissible sets a and/3 are chosen. We observe that

they have to be non-empty since by Lemma 7.6 we have ,40 =/}0 = 0.

By ~Z/~ = 1, for each single/3,1/31 ~< k, the probability to be chosen is at least

Calculating the probability of a set a to be chosen is a bit more complicated.

First we will bound the sum over the absolute values of the coefficients of all

admissible sets a.

E ['4~[ ~ E A21 1 (7.14)

(*) Lemma 7.5 ~"

-: I,~l~<k,iA,, [>/Y -: I,~l~<k,lA,, [~>'r

Here, inequality (*)is obtained by multiplying each single term [Aa[ with

By (7.14), each admissible a is chosen with probability at least [Am[ 7.

We will now calculate the probability that the provers return a

compatible

pair

(x, y) to the verifier, i.e. a pair with

x = y~V.

Since the provers choose independently, each possible pair of sets (a,/3) is chosen

with probability at least 7 [Aa[/}~. Once the provers have chosen a pair (a,/3)

192 Chapter 7. Bounds for Approximating MAXLINEQ3-2 and MAxEkSAT

containing some x E c~,y E ~ with

x = y~V,

they will return such a compatible

pair (x, y) to the verifier with probability at least ~ since loci, ]El ~ k.

Overall, the probability of returning to the verifier some ( x, y) such that

x = y'~V

is at least

Z Z

where the inequality holds by the assumption.

As pointed out above, ]~ contains only assignments for Var(r which satisfy

r Consequently, the verifier has to accept any compatible pair ( x, y) it gets

from the provers (see Protocol 6.2). Thus the above probability of choosing a

compatible pair already gives the success probability of the prover strategies

under the condition that the clauses in r have disjoint sets of variables.

Since by ]~1/>

re(v)

this condition is fulfilled with probability at least 1/2, the

unconditional success rate of the prover strategies is at least 4k-~" 9

7.5 An Optimal Lower Bound for Approximating

MAxLxNEQ3-2

As explained earlier, the proof of Theorem 7.1 is a reduction from ~0-ROBE3SAT -

b, and this reduction is based on a certain verifier for e0-RoBE3SAT-b. We first

present this verifier. We then explain the completeness and soundness properties

it enjoys. A description of the reduction from 6o-ROBE3SAT-b follows.

7.5.1 The Verifier

The verifier essentially implements a basic test as described in Subsection ?.3.3.

For technical reasons, the verifier rejects short formulae in Step 1.

Verifier Vlin[J, v 1.

Input:

An instance

~ = C1 A C2 A ... ACm of ~0-ROBE3SAT-b.

Proof:

A pair

((AV)ve(V~(~,)),

(Br162 such that (7.5) - (7.7) hold.

1. If (~) is empty, then reject.

2. Choose

(r f, gl,g2) E f~

according to the distribution D~ (see Subsec-

tion 7.3.3).

3. If

AV (f) 9 B'P(gl) - Be(g2)

= 1, (7.15)

then accept, else reject. (See also (7.2) and (7.4), and Subsection 7.3.2.)

7.5. An Optimal Lower Bound for Approximating MAxLINEQ3-2 193

7.5.2 Completeness

We first show that verifier Vlin[6, v] has the following completeness property.

Lemma 7.9 (completeness of the verifier). Let 6, v > O. Then there exists

a constant ml (v) such that for every satisfiable input with at least ml (v) clauses,

the verifier Vlin[6, v] accepts some 7r as a proof for ~ with probability at least

1-6.

Proof. First of all, if ~ is short, then Vlin[6, v] will reject in Step 1, no matter

what the proof looks like.

On the other hand, if ~o is long enough, i.e., if the number of clauses is greater

than 3Iv (l being the constant which bounds the number of occurrences of

each variable in an c0-ROBE3SAT-b instance), then (~) will not be empty and

Vlin[6, v] will always pass Step 1 and choose (r V, f, gl, g2) as determined by

D ~ We show that there is a proof such that regardless of which r and V the

verifier chooses, it will accept with probability 1 - 6 after Step 1.

Let z be a satisfying assignment for ~ and consider the proof 7r defined by

AV(f) = f(zTY),

SO(g) = g(zl"Var(r

for V e (va~(v)), I:B V ~ B, r e (~), and g:B vat(C) -+ B.

By construction, AV (f) = /(ztV), Br = g~(zT Var(O)), and Be(g2) =

g2(zTVar(r This is true as A v and B ~' are in fact long codes and moreover,

B r is the long code of a satisfying assignment for r (see (7.2) and (7.4)).

From the definition of D~ follows that f(zTV) "gt (z't Vat(C)) "g2 (zl" Vat(C)) = 1

with probability 1 - 6. So ~r is accepted as a proof for ~o with probability at least

1-5. 9

Observe that unlike usually we do not have perfect completeness for the veri-

fier; the distribution D O introduces an error with probability 5. The following

consideration gives a motivation for this.

Since the test in Step 3 is linear, it will not only let pass any legal long code but

also any linear combination of long codes. The error introduced by D o ensures

that linear combinations with less summands get more attention (see details in

the proof of Lemma 7.10).