Mayr E.W., Pr?mel H.J., Steger A. (eds.) Lectures on Proof Verification and Approximation Algorithms

Подождите немного. Документ загружается.

5. Proving the PCP-Theorem

Volker Heun, Wolfgang Merkle, Ulrich Weigand

5.1 Introduction and Overview

The PCP-Theorem states that Af:P is equal to the class PCP(logn, 1) of lan-

guages which are recognized by verifiers which on an input of length n use at

most O(log n) random bits and query only O(1) positions of their proofs. In the

following we give an essentially self-contained account of the PCP-Theorem and

its proof which is based on the original work due to Arora [Aro94], Arora, Lund,

Motwani, Sudan, and Szegedy [ALM+92], and Arora and Safra [AS92]. We also

use ideas and concepts from the presentation given by Hougardy, PrSmel, and

Steger [HPS94].

In this section, we give an outline of the proof of the PCP-Theorem, which

states that AfT ~ = PCP(log n, 1). As an implication of Proposition 4.2, we obtain

PCP(log n, 1) C_ flfT~. Hence it remains to show the reverse containment AfT ) C_

PCP(log n, 1). Clearly, it is sufficient to show that an Af:P-complete problem is

contained in PCP(logn, 1). In the remainder of this chapter, we will prove that

3SAT E PCP(Iog n, 1), which completes the proof of the PCP-Theorem.

The structure of the proof that 3SAT E PCP(log n, 1) is illustrated in Figure 5.1.

As introduced in Chapter 4, PCP(r, q) denotes the class of languages with prob-

abilistically checkable proofs such that a verifier requires O(r) random bits and

queries O(q) bits. In this figure only, constant-PCP(r, q) denotes the restricted

class of languages with probabilistically checkable proofs, where the verifier is

restricted to query the O(q) bits from a constant number of segments. Here a

segment is a contiguous block of O(q) bit positions.

Obviously, a satisfying assignment of a given Boolean formula is a proof of its

satisfiability. But clearly it is not sufficient to read only a constant number of

bits of this proof for a verification. A key idea is to extend such a proof using

linear functions from ~ into F2, where the images of basis vectors depend on

the given assignment in a more or less natural way. Due to the linearity the

images of the basis vectors of F~2 determine the images of all other vectors

and m will be a polynomial in the length of the given Boolean formula. The

details will be explained in Section 5.3. We will refer to this encoding as linear

code and in general we call the conversion of an assignment into a function

an arithmetization. A proof will be constructed from the linear code by listing

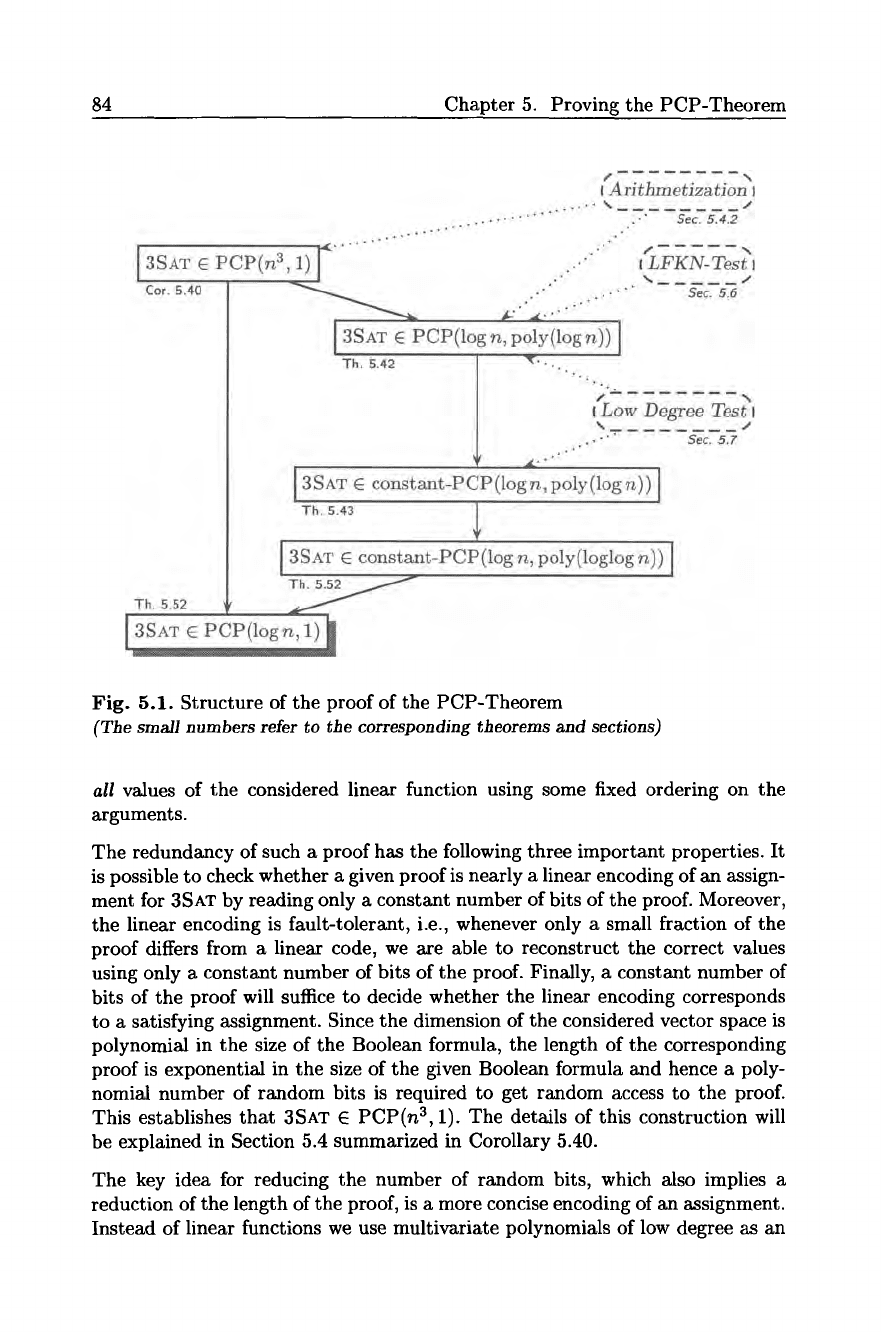
84 Chapter 5. Proving the PCP-Theorem

Fig. 5.1. Structure of the proof of the PCP-Theorem

(The

sma/l numbers refer

to the corresponding

theorems and

sections)

all

values of the considered linear function using some fixed ordering on the

arguments.

The redundancy of such a proof has the following three important properties. It

is possible to check whether a given proof is nearly a linear encoding of an assign-

ment for 3SAT by reading only a constant number of bits of the proof. Moreover,

the linear encoding is fault-tolerant, i.e., whenever only a small fraction of the

proof differs from a linear code, we are able to reconstruct the correct values

using only a constant number of bits of the proof. Finally, a constant number of

bits of the proof will suffice to decide whether the linear encoding corresponds

to a satisfying assignment. Since the dimension of the considered vector space is

polynomial in the size of the Boolean formula, the length of the corresponding

proof is exponential in the size of the given Boolean formula and hence a poly-

nomial number of random bits is required to get random access to the proof.

This establishes that 3SAT E PCP(n 3, 1). The details of this construction will

be explained in Section 5.4 summarized in Corollary 5.40.

The key idea for reducing the number of random bits, which also implies a

reduction of the length of the proof, is a more concise encoding of an assignment.

Instead of linear functions we use multivariate polynomials of low degree as an

5.2. Extended and Constant Verifiers 85

encoding. We will refer to such an encoding based on multivariate polynomials

as the

polynomial code.

In this case the length of such an encoding will be

polynomially related to the size of the given Boolean formula as we will see

in Section 5.3. The polynomial code has similar properties as the linear code.

It is possible to verify whether a given proof is a polynomial encoding of an

assignment and the polynomial code is fanlt-tolerant. Unfortunately, for the

verification and the reconstruction a polylogarithmic number of bits of the proof

have to be inspected. Nevertheless, this is the second major step in proving the

PCP-Theorem and will be stated in Theorem 5.42. The details will be given

in Section 5.4. The proof of these details is rather complicated and requires

mathematical tools like the so-called LFKN-Test (cf. Section 5.6) and the Low

Degree Test (cf. Section 5.7). As shown in Section 5.4 the result can be improved

in the following sense. There exists a probabilistically checkable proof for 3SAT

such that only a constant number of 'contiguous blocks' of polylogarithmic length

have to be inspected by the verifier instead of polylogarithmic bits at arbitrary

positions, which will be shown in Theorem 5.43.

As we will see in Section 5.5 it is possible to compose two verifiers. This is

the main idea for a further reduction of the number of queried bits while the

length of the proof does not increase significantly. First, the proof system based

on the polynomial code is composed with itself obtaining a probabilistically

checkable proof of polynomial length, where only a constant number of blocks of

size O(poly(loglog n)) have to be inspected by the verifier. Then these blocks of

length O(poly(loglog n)) in the composed proof system will be encoded using the

proof system based on linear codes. So we obtain a proof system of polynomial

length where only a constant number of bits have to be inspected by the verifier.

This will be discussed in detail in Section 5.5 and summarized in Theorem 5.52.

As a consequence we obtain AlP = PCP(logn, 1) as stated in Theorem 5.53.

5.2 Extended and Constant Verifiers

Extended Verifiers.

We formulate the proof of the PCP-Theorem in terms of

extended verifiers as introduced in Definition 5.1. Extended verifiers resemble

rather closely usual verifiers as introduced in Chapter 4, however, there are two

main differences. Firstly, the input of an extended verifier is not a single argument

x, but a pair (x, vo) of arguments where ~0 is a designated part of the proof.

Secondly, extended verifiers are not exclusively designed to accept a subset of

all possible inputs in the sense that for every input (x, to) the extended verifier

either accepts or rejects (x, ~r0) with high probability: we will consider extended

verifiers where for example there are such pairs which are accepted and rejected

with equal probability of 1/2.

Definition 5.1.

extended verifier

V is a polynomial time bounded Turing

machine which, besides its input tape and its work tapes, has access to a binary

random string T and to a proof it = (7ro, ~1) where we assume that

86 Chapter 5. Proving the PCP-Theorem

V has random access to the binary strings 7ro and 7rl, that is, V can access

single bits of these strings by writing corresponding queries on a special oracle

tape,

- V queries 7r non-adaptively, that is, the queries to the proof might depend on

the input and the random string, but not on the answers to previous queries

to the proof.

Here we assume, firstly, that the random string T is obtained by independent

tosses of a fair coin and, secondly, that the length of 7- can be computed from

the length of the input x in polynomial time. (Thus in particular we cannot hide

information in the length of the supplied random string.)

An extended verifier Y accepts (x, (Tr0,7rl)) on random string 7- iff V eventually

halts in an accepting state while working on x, to, 7rl, and T, and otherwise V

rejects (x, (r0,7rl)) on random string T.

An extended verifier V accepts (x, (Tro, 7h)) iff V accepts this pair on all random

strings, and V rejects (x, (Tro,Th)) iff V accepts this pair on at most 1/4 of all

random strings.

An extended verifier V accepts the input (x, ~ro) iff there is some binary string

7r 1

such that V accepts (x, (Tro,Th)) and V rejects the input (x,~ro) iff V rejects

(X, (71"0,71"1))

for all binary strings rrl.

Given an extended verifier V, we denote by A[V] the set of all pairs (x, r0) which

V accepts, and by R[V] the set of all such pairs which V rejects.

Observe that in connection with extended verifiers we use several variants of

accepting and rejecting and that we assume that it will always be clear from the

context which variant is meant.

An extended verifier queries its proofs non-adaptively and thus it is convenient

to assume that the answers to its queries are given simultaneously as a finite

binary string written on some designated tape. In addition we assume that there

is some appropriate mechanism to indicate queries beyond the end of the strings

7r0 or 7rl. Observe that for resource bounded extended verifiers as considered in

the following it does not really matter whether we assume that the proofs r0

and 7rl are given as binary strings or as an infinite set oracle because anyway

such an extended verifier can access just a finite part of its proof.

Resource Bounds for Extended Verifiers. We are mainly interested in extended

verifiers with additional bounds on the length of the supplied random string and

on the number of bits the verifier reads from the proof. Observe in connection

with Definition 5.2 that we use for example the notation r, as well as r(n), in

order to refer to the resource bound obtained by applying the function r to

the length n of the input string. Observe further that for technical reasons we

consider only resource bounds which are non-decreasing and can be computed

from the argument n in time polynomial in n.

5.2. Extended and Constant Verifiers 87

Definition 5.2. An extended verifier is (r, q)-restricted iff there is some con-

stant c such that on every input x of length n, the random tape holds a random

string r Of length c. r(n) and for each given random string, V queries at most

c . q(n) bits of the proof 7r.

For classes Yr o and J:l o/functions from naturals to naturals, an extended verifier

is (~o, ~'l)-restricted if it is (r, q)-restricted for functions r in Yro and q in :7:1.

Remark 5.3. In Definition 5.1 the constant 1/4 can be replaced by an arbitrary

value in the open interval between 0 and I without changing the introduced con-

cepts. This can be shown by applying the well-known technique of probability

amplification. More precisely, we run a verifier repeatedly for a constant number

of times while using independent parts of the random strings for each iteration,

and we accept if[ all the iterations result in acceptance. Observe that this remark

also applies to (r, q)-restricted extended verifiers, because iterating the compu-

tation a constant number of times will increase the amount of resources used

only by a constant factor.

Verifiers and Extended Verifiers. Remark 5.4 shows that extended verifiers are

a generalization of the usual concept of verifier.

Remark 5.4. Given a verifier Vo, we can easily construct an extended verifier

V1 which on input x and proof (rro,Trl) simply behaves as Vo does on input x

and proof ~q. Both verifiers are equivalent in the sense that for all inputs x and

for all proofs 7r0, the verifier Vo accepts x iff the extended verifier V1 accepts the

pair (x, 7to), and likewise for rejectance.

Conversely consider an extended verifier 1/1 with the special property that for

each input x, either there is some proof fro where V1 accepts the input (x, 7to)

or for all proofs 7to, the input (x, Tro) is rejected. Then it is straightforward to

construct a verifier V0 which accepts exactly the strings x of the former type,

that is, the strings in the set

{x I there is some proof fro where 1/1 accepts the input (x, 7to)}.

More precisely, the verifier Vo on input x and proof 7r interprets 7r as a pair

(Tro, 7h) and then works as the extended verifier V1.

For example consider solution verifiers as introduced in Definition 5.33 below.

A solution verifier is a special type of extended verifier which accepts the pair

(x, 7to) iff 7to is a code for a satisfying assignment of the 3-CNF-formula x and

which rejects the pair if ~ro does not agree with such an encoding on most places.

As a consequence solution verifiers indeed have the special property that for each

input x either there is some proof 1to where the input (x, 7to) is accepted or for all

proofs to, the input (x, 7to) is rejected. Here the two cases correspond to x being

satisfiable, respectively being not satisfiable. By the discussion in the preceding

paragraph solution verifiers can thus be viewed as verifiers which accept 3SAT,

the set of satisfiable 3-CNF-formulae.

88 Chapter 5. Proving the PCP-Theorem

Recall that in contrast to the case of verifiers with extended verifiers there might

be inputs (x, 1to) which are neither accepted nor rejected. Example 5.5 gives some

indication why this relaxation is reasonable.

Example 5.5. In the sequel we will construct extended verifiers which accept

a pair (0 n, 7r0) in case 7r0 is a codeword in some given code Cn, and which reject

the pair in case 7to does not agree with a codeword in Ca on at least a 5o-fraction

of its places where ~o is close to, but strictly below 1. Moreover while working

on a single random string these extended verifiers read only a small part of the

alleged codeword ~r0. In this situation we should expect that pairs (0 n, 7r0) where

1to is not in C,~, but is close enough to a codeword in Cn, are accepted on more

than one quarter of all random strings, but not for all random strings, that is,

there are inputs which are neither accepted nor rejected.

Constant Extended Verifiers. In Section 5.4 we will introduce solution verifiers

which are a special type of extended verifiers. The introduction of such solution

verifiers is mainly motivated by the fact that under certain restrictions a verifier

and a solution verifiers can be composed in order to yield a more efficient verifier,

see Lemma 5.51. In connection with such compositions we are led to consider

verifiers which query the proof not at arbitrarily scattered places, but access

only a constant number of contiguous subwords of the proof. Observe that this

might amount to a restriction only in the presence of additional bounds on the

total number of queries to the proof, because otherwise the verifier could just

query all places.

Definition 5.6. A segment is a subset of the natural numbers of the form

{i I n <~ i ~ m} where n and m are arbitrary natural numbers. A verifier V

is constant iff there is some constant c such that for all inputs x, the sets of

positions at which V queries the proofs 7to and 7rl, respectively, are both equal to

the union of at most c segments.

Observe that a constant (r, q)-restricted verifier queries constantly many seg-

ments each of length at most O(q), and that an (r, 1)-restricted verifier is always

constant.

5.3 Encodings

5.3.1 Codes

In Section 5.4 we will introduce solution verifiers as a special form of extended

verifiers. A solution verifier interprets its input x as a Boolean formula and

expects the input 7to to be an encoded assignment for this formula. Before we

consider solution verifiers in detail, we compile some material on codes.

5.3. Encodings 89

Definition 5.7.

An alphabet is a finite set of symbols. A string over an alphabet

is a finite sequence of symbols from Z.

For a rational 5 in the open interval between 0 and 1, two strings are

5-close

iff

they have the same length and disagree on at most a 5-fraction of their places.

A string is 6-close to a set of strings if] it is 5-close to some string in the set.

A code

is a set C of strings over some fixed alphabet ~ such that all strings in

C have the same length and for all

5 < 1/2

no pair of distinct strings in C is

5-close. The elements of a code C are denoted as

codewords

and their length is

the

codeword length

of C.

Let C be a code and let n be an arbitrary natural number. Then every function

dec

from C onto

{0, 1} n

is called a

decoding function

for C. In this situation a

codeword y is a

code for

the binary string x iff

dec(y)

is equal to x.

A coding scheme

is a sequence (Co,

deco), (Cx, dec1),..,

where for every natural

number n, the function

decn

is a decoding function for Cn with range

{0, 1) n.

Given such a coding scheme we write En, Sn, and kn for the alphabet, the alphabet

size, and the codeword length, respectively, of the code Cn.

Observe that given a decoding function from some code to ~0,1} '~, for every

binary string of length n, there is some associated codeword, but in general this

codeword is not unique. A coding scheme can be viewed as a rule which yields

for every natural number n a method to encode strings of length n. The concept

coding scheme is not designed to distinguish encodings of strings of mixed length

and correspondingly the codes Co, 6'1,.. 9 of a coding scheme are not required to

be disjoint and might be over arbitrary alphabets S0, ~1,....

Remark 5.8. In the sequel we will consider extended verifiers which expect

parts of their proof to be encoded according to some given coding scheme. Now

the tape alphabet of an extended verifier contains only the symbols 0 and 1,

and accordingly we have to represent codewords over the alphabets Eo, Z1,...

as binary strings. Given an alphabet ~ of size s this is easily done by first rep-

resenting the symbols in E in some canonical fashion by binary strings of length

[log s], then extending this representation to a homomorphism from strings over

~n to binary strings. We denote the image of a word over ~ under such a homo-

morphism as

associated binary codeword

or string, and accordingly we speak of

the length of the binary codewords. In case we use strings over some arbitrary

alphabet ~ as part of the input of an extended verifier, it is to be understood

that the tapes of the verifier actually hold the associated binary string. In order

to avoid confusion with the symbols of the alphabet E we refer to the symbols of

an associated binary codeword by the term bits. Observe that we have to scan

[log s] bits of the associated binary string in order to read a single symbol of a

string over an alphabet of size s.

90 Chapter 5. Proving the PCP-Theorem

5.3.2 Robust Coding Schemes

Efficient Operations on Codewords. The motivation for using codes in connec-

tion with extended verifiers comes from the fact that certain tests on strings can

be performed more efficiently on the associated codewords than on the strings

themselves. For an example see Example 5.9 where it is shown that for every

(i < 1/8 and for all pairs of strings which are both known to be (f-close to code-

words in some code, in order to check probabilistically whether both strings are

in fact close to the same codeword it suffices to scan O(1) randomly selected

symbols.

Example 5.9. We let 6 < 1/8 be some arbitrary constant and consider strings

v and w which are both (f-close to a code C. Then for both strings there is a

unique nearest codeword in C. If we assume that the nearest codewords of v

and w are the same then v and w must be 2(i-close. On the other hand, if the

nearest codewords are different, then they can agree on at most 1/2 of their

places, and consequently v and w are not even (io-close for (io := 1/2 - 25, where

by assumption on (i we have 1/2 - 2(i > 1/4.

So trying to find a disagreement between v and w by comparing the two strings at

some place chosen uniformly at random amounts to a Bernoulli trial with success

probability 25 < 1/4 in case the two strings are close to the same codeword

and with success probability 60 > 1/4, otherwise. As a consequence we can

distinguish the two cases probabilistically. More precisely probability theory tells

us that for every e > 0 there is a constant c such that if we repeat the Bernoulli

trial 4c times then with probability 1 - ~ the accumulated number of successes

is strictly below c in the first case and is strictly above c in the second.

Now consider a coding scheme (Co, dec0), (C1, dec1),..., let sn be the size of the

alphabet En, let kn be the codeword length of Cn and assume that sn and kn can

be computed from n in time polynomial in n. Then by the preceding remarks for

every (i < 1/8 there is a ([log kn], [log sn])-restricted extended verifier which for

all strings v and w over En which are (i-close to Cn, accepts the input (O n, vw)

in case v is equal to w, but rejects it in case v and w are not (f-close to the same

codeword.

Robust Coding Schemes. The probabilistic test for being close to the same code-

word given in Example 5.9 is more efficient than comparing the corresponding

non-encoded strings bit by bit. In the verification of the test however we have

to assume that the input indeed contains strings which are close to codewords.

We will show next that this is not a real restriction in case there is an appro-

priately restricted extended verifier which simply rejects all inputs where the

strings under consideration are not close to codewords. Likewise we will con-

sider probabilistic tests where during the verification we not just assume that

the input contains strings close to a certain code, but also that at all positions

scanned these strings indeed agree with the nearest codeword. Again this is not

5.3. Encodings 91

a real restriction in case, firstly, for each fixed random string, the probabilistic

test under consideration scans the strings under consideration only at constantly

many symbol and, secondly, for each such symbol, we can probabilistically test

for agreement with the nearest codeword within the given resource bounds.

Unlike for the probabilistic test for being close to the same codeword given

in Example 5.9 which works for arbitrary coding schemes in the case of tests

for closeness to a codeword and for agreement with the nearest codeword at

some given place we should not expect that there is a general procedure which

works for coding schemes of different types. There are however such procedures

for specific coding schemes, and in particular so for two coding schemes based

on linear functions and on polynomials, respectively, which we will introduce

in Sections 5.3.3 and 5.3.4. Using the notation introduced in Definition 5.10

these coding schemes will be shown to be (n, 1)- and (log

poly(log n))-robust,

respectively.

Definition 5.10.

Let C be a coding scheme

(C0,dec0), (Cl,decl),....

The coding scheme C is (r,

q)-checkable

iff there is a positive rational 5o where

for every 0 < 5 <<. 50 there is a constant

(r,

q)-restricted extended verifier V such

that, firstly, V accepts every pair (O n, 7to) where 7to is in C,~ and, secondly, V

rejects every pair

(On,Tro)

where 7to is not 5-close to a codeword in C,~.

The coding scheme g is

(r, q)-correctable

iff there is a constant

(r,

q)-restricted

extended verifier V and a positive rational

51 < 1/4

such that, firstly, V accepts

every pair ((O n, i), 7to) where 7to is a eodeword z in C,~ and, secondly, V rejects

every pair

((On,i),Tro)

where 7to is 51-close to a codeword z in Cn but 7to and z

disagree at the i-th symbol. (Observe that the eodeword z is uniquely determined

because 51 is less than

1/4.)

The coding scheme g is (r,

q)-robust

iff it is (r, q)-checkable and (r, q)-correctable.

A positive rational 5 witnesses that g is (r, q)-checkable iffC satisfy the definition

of (r,

q)-checkable with 50 = 5, and likewise we define a concept of witness for

(r, q)-correctable coding schemes. A positive rational 5 witnesses that C is

(r, q)-

robust iff 5 witnesses both that g is (r, q)-checkable and that g is

(r,

q)-correctable.

Observe that for all three properties introduced in Definition 5.10 the class of

witnessing rationals is closed downwards in the sense that if a positive rational

5 witnesses one of these properties then so does every positive rational smaller

than 5.

We will show in the remainder of this section that, intuitively speaking, in case

an extended verifier V expects that its proof contains at some specified places

codewords according to some (r, q)-robust coding scheme then under certain

conditions we can assume during the verification of V's behavior that the proof

contains at these places indeed codewords and not just arbitrary binary strings.

Before we give a formal statement of this remark in Proposition 5.14 we demon-

strate the techniques used in Examples 5.11 and 5.12.

92 Chapter 5. Proving the PCP-Theorem

Example 5.11. Let C be a coding scheme with codes C0,C1, .... Let r and q

be resource bounds such that

has codeword length in 2 ~ and is over

an alphabet ~a of size in 2 ~ According to Example 5.9 there is an (r, q)-

restricted extended verifier Vo and a positive rational 5 < 1/8 such that for all

strings v and w over ~n which are (i-close to

Ca, Vo

accepts the input (0a,vw)

in case v is equal to w, but rejects it in case v and w are not (i-close to the same

codeword.

Now in case the coding scheme C is in addition (r, q)-checkable then we can drop

the condition that v and w are (f-close to C,~, that is, there is an (r, q)-restricted

extended verifier V1 which for all strings v and w over ~a, accepts the input

(0 a, vw)

in case v and w are identical codewords in

and rejects in case v and

w are not (f-close to the same codeword in

Ca.

On an input (O n,

vw)

the extended verifier 111 runs a subverifier in order to check

probabilistically whether both of v and w are (i-close to a codeword in Ca. In

case this test fails then V1 rejects immediately and otherwise, V1 just simulates

V0 on the given input.

Now consider Vl'S behavior on input

(Oa,vw).

In case v and w are identical

codewords in C,~ then by construction V1 accepts. On the other hand in case v

or w is not (i-close to Ca then V1 rejects due to the initial test, and in case both

are (i-close to Ca but their respective nearest codewords differ then V1 rejects by

assumption on V0.

Example 5.12 shows a more involved application of subverifiers where the input

for the subverifier depends on the random string. While the argument in Exam-

ple 5.12 is basically the same as in the proof of Lemma 5.51 about composing

verifiers, we refrain from stating the underlying technique in full generality.

Example 5.12. Let C be a coding scheme with codes Co, C1,.... Consider the

following simple test for identity of two codewords from

Ca:

select uniformly at

random a position between 1 and the codeword length of Ca and compare the

codewords at this place; accept in case the symbols read are the same and reject,

otherwise. Observe that in case both codewords are the same the test accepts

with probability 1, but otherwise it rejects with probability at least 1/2. It is

now straightforward to construct an extended verifier Vo which for every input

(0 n, vw)

where v and w are codewords in Ca, accepts in case v and w are equal

and rejects, otherwise. The extended verifier Vo simply runs the above test k

times while using independent parts of its random string for each repetition and

V0 rejects in case one of the repetitions results in rejection. Thus V0 rejects with

probability of at least 1 -

1/2 k

in case v and w are different codewords in Ca.

The extended verifier 110 requires only k Flog kn~ random bits and reads only

k Flog

sa~

bits of its proof where sa and ka are the alphabet size and the codeword

length of code Ca. Thus in general V0 will be more efficient than the extended

verifier constructed in Example 5.9. However the latter verifier just assumes