Маятник Максвелла
Подождите немного. Документ загружается.

ст. преп. Виноглядов В.Н.
Лабораторная работа № 1-3
Маятник Максвелла
Цель работы: экспериментальное определение момента инерции тела вращения, изучение уравнения
вращательного движения, проверка точности работы прибора “Маятник Максвелла”.
Приборы и принадлежности:
маятник Максвелла, набор металлических накладных колец.
Описание экспериментальной установки.
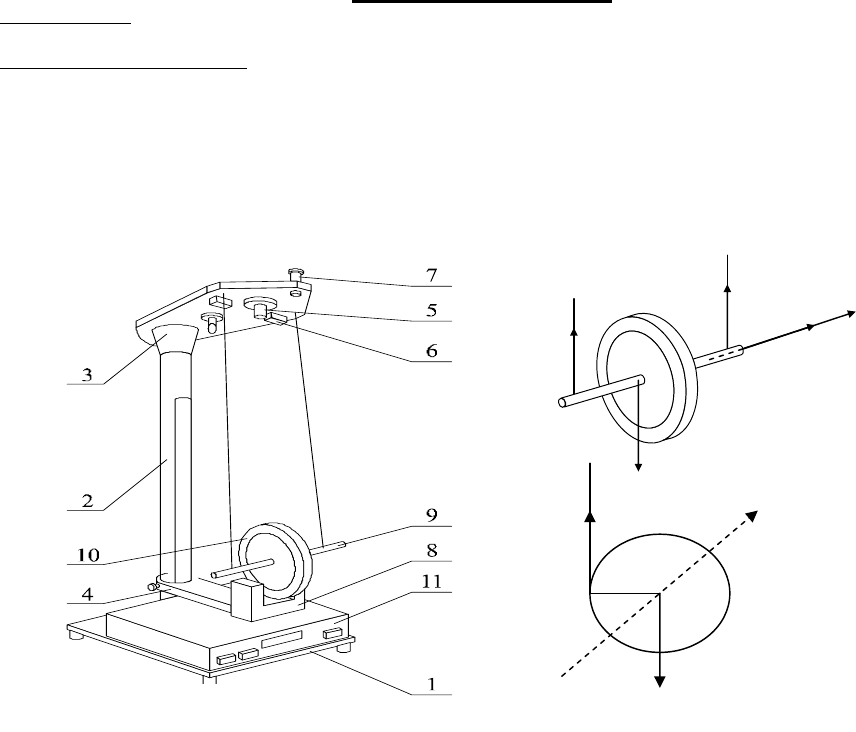
Данная установка для определения момента инерции тел вращения называется маятником Максвелла. Общий вид
маятника Максвелла приведён на рис. 1.
На основании 1 закреплена стойка 2, к которой прикреплены неподвижный верхний кронштейн 3 и подвижный
кронштейн 4. На верхнем кронштейне находится электромагнит 5, фотоэлектрический датчик №1 (6) и вороток с
фиксатором 7 для закрепления и регулировки длины бифилярного маятника.
Нижний
кронштейн 4 с фотодатчиком № 2 (8) можно перемещать вдоль стойки и фиксировать в выбранном
положении. Маятник 9 — это диск, закрепленный на оси и подвешенный на бифилярном подвесе. На диск
накладываются сменные металлические кольца 10, изменяющие момент инерции системы. Маятник с наложенным
кольцом удерживается в верхнем положении электромагнитом. Длина маятника определяется по миллиметровой шкале
стойки
прибора. Сигналы с фотодатчиков служат для автоматического пуска и остановки миллисекундомера 11.
Основные теоретические сведения
Маятник Максвелла служит для определения момента инерции тел.
Небольшой диск (маховичок), насаженный туго на ось опускается под действием силы тяжести на двух нитях,
предварительно намотанных на ось маховичка. Нити во время движения разматываются до полной длины,
раскрутившийся маховичок продолжает вращательное движение в том же направлении и наматывает нити на ось, в
следствии чего он поднимается вверх, замедляя при этом вращение. Дойдя до верхней точки, диск опять опускается
вниз и т.д. Маховичок будет совершать колебания вверх и вниз, поэтому устройство и называют маятником. Введем
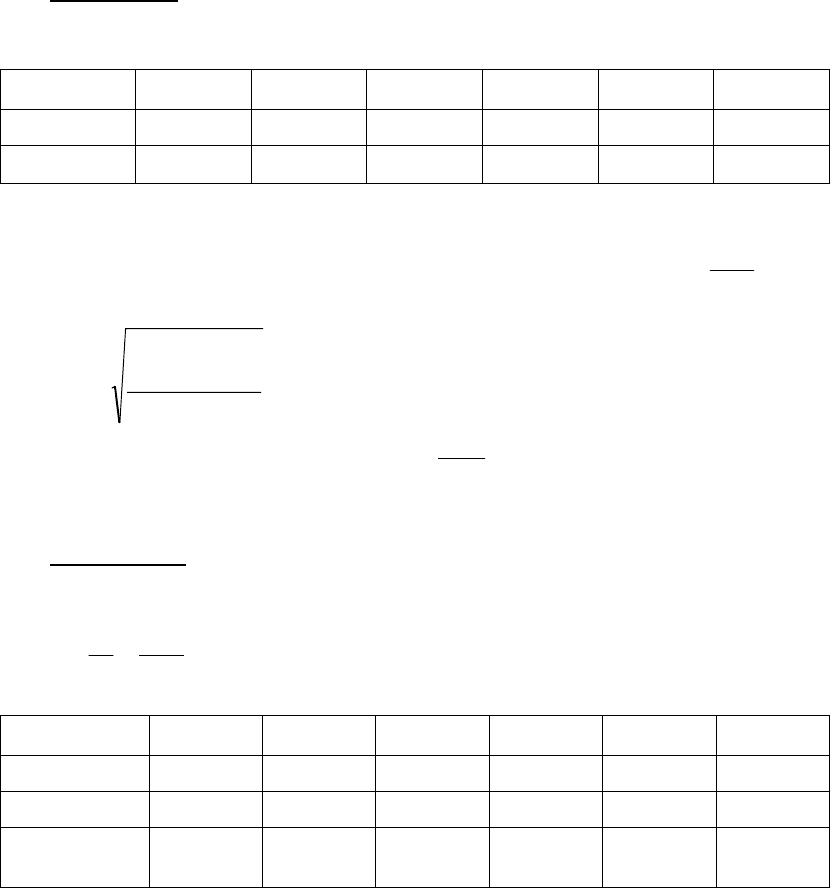
следующие обозначения: (рис. 2)
gm
r
— сила тяготения;
T
r
— сила натяжения одной нити;
R
— радиус валика;
I
—
момент инерции маховичка; тогда уравнение для поступательного движения можно записать так:
maTmg
=
−
2 (1)
где
a
— ускорение центра масс, а уравнение для вращательного движения
ε
IagmrM
=
−
=
)(
(2)
где
M
— момент действующих сил. С учетом уравнения (1), момент действующих сил
ε
IagmrM
=
−
=
)( .
Рисунок 2.
T
v
T
v
gm
r
M
r
υ
r
ε
r
ω
r
T
v
d
gm
r
M
r
Рисунок 1.
Подготовка прибора к работе
1. На диск маятника наложить стальное кольцо, указанное преподавателем.
2. Убедиться, что край стального кольца находится примерно на 2 мм ниже оптической оси
нижнего фотоэлектрического датчика. Если нет, отрегулировать высоту нижнего кронштейна с
фотоэлектрическим датчиком.
3. Намотать на ось маятника нить подвеса, укладывая ее равномерно, виток к витку. Проверить,
отвечает ли нижняя
грань кольца нулю на стойке. Если нет, разфиксировать верхний кронштейн и
отрегулировать его высоту и еще раз вернуться к п.2.
4. Включить кнопку «Сеть».
5. Нажать клавишу «Пуск» миллисекундомера.
6. Намотать на ось маятника нить подвески.
7. Зафиксировать маятник с помощью электромагнита, не слишком туго закручивая нить.
8. Повернуть маятник
в направлении движения на угол около
o
5 .
9. Последовательно нажать клавиши «Сброс» и «Пуск».
10. Прочитать измеренное значение времени падения маятника и занести его в таблицу 3.1.
Порядок выполнения работы
Упражнение I. Проверка точности работы прибора и определение дисперсии опыта.
1. Установите нижний кронштейн на отметке, заданной преподавателем. Проведите пять замеров
времени падения маятника. Результаты занесите в таблицу 3.1.
Таблица 3.1.
N
оп
1 2 3 4 5
∑
i
t
( ><− tt
i
2. Вычислите среднее значение времени по формуле
5
5
1
∑
=
>=<
t
i
t
t
и заполните табл.3.1.
3. Определите среднеквадратичное отклонение
)1(
)(
5
1
2
−
><−
−
∑
=
><
n
tt
S
t
i
t
, где
n
- число опытов.
4. Проверьте неравенство
05,0≤
><
><
t
S
t
— установка работает нормально. В этом случае
переходите к выполнению упражнения 2. Если не выполняется то обращайтесь за помощью к
обслуживающему персоналу или преподавателю.
Упражнение II.
Определение углового ускорения маятника и его дисперсии.
1. Используйте данные первого упражнения, заполните таблицу 3.2., где угловое ускорение
ε
рассчитывается по формуле
rt
h2
r
a
2
i
⋅
==ε
ε
Таблица 3.2.
N
оп
1 2 3 4 5
∑
i
t
i
ε
)
( ><−
εε
i
2. Вычислите среднее значение углового ускорения для заданной высоты и его дисперсии по
формулам
5
5
1
∑
=
>=<
i
i
ε
ε
;
)1(
)(
5
1
2
−
><−
=
∑
=
><
nn
S
i
i
εε
ε
Результаты запишите в виде:
><
±>=<
ε
ε
ε
S
.
Упражнение III.
Проверка равноускоренности движения маятника.
Высота и время падения маятника связаны соотношением
2
2
at
h =
. Рассмотрим зависимость
h
a
t
2
=
, для
дальнейших расчетов введем следующие обозначения:
ii
ty
=
;
ii
hx =
;
a
A
2
=
.
1. Установите заданную преподавателем высоту падения с 5-ти различных высот и занесите
результаты в таблицу 3.3. С каждой высоты сделайте 3 замера времени падения маятника, а среднее
значение занесите в таблицу.
Таблица 3.3.
i
h
i
t
i
x
i
y
2
i
x
ii
yx
2
)(
ii
Axy −
2. Определить параметр A по формуле метода наименьших квадратов
∑
∑
=
2
i
ii
x
yx
A
, затем
определите дисперсию адекватности
1
)(
2
2
−
−
=
∑
n
Axy
S
ii
ад
.
3. Вычислить критерий Фишера
2
2
оп
ад
S
S
F =
. Если
таблрасч
FF
≤
, движение можно считать
равноускоренным. Дисперсию опыта взять из упражнения I.
4. Постройте график зависимости
Axy
=
и убедитесь, что экспериментальные точки лежат
вблизи прямой.
Упражнение IV.
Проверка соотношения
ε
r
r
M
.
Уравнение вращательного движения маятника имеет следующий вид:
ε
r
r
IM =
. Откуда следует, что
ε
r
r
M
I =
.
Поскольку
r
a
ε
=
, то изменяя радиус оси маятника, меняется ускорение поступательного движения. Для дальнейших
расчетов введем следующие обозначения:
i
i
ii
r
a
y ==
ε
;
)(
iii
agmrMx −==
, где
2
2
i
i
t
h
a =
;
I
A
1
=
.
1. Изменяя с помощью подвижных втулок радиус оси маятника, проведите замеры времени
падения маятника. Результаты занесите в таблицу 3.4.
Таблица 3.4.
i
r
i
t
h
i
a
i
x
i
y
i
yx
2
i
x
(
ii
Axy −
2. Рассчитайте по формулам
i
a
;
i
x
;
i
y
.Результаты занесите в таблицу 3.4. Для проверки соответствия
зависимости
Axy =
определим параметр
A
и дисперсию адекватности по формулам:
∑
∑
=
=
=
4
1
2
4
1
i
i
i
i
i
x
yx
A
;
)1(
)(
4
1
2
2
−
−
=
∑
=
n
Axy
S
i
ii
ag
.
3. Постройте график зависимости
Axy =
, отметьте экспериментальные точки.
4. Вычислите критерий Фишера по следующим формулам:
2
2
on
ag
S
S
F =
, где в качестве дисперсии опыта возьмите
дисперсию углового ускорения, найденную во втором упражнении
)(
22
><
=
xon
SS
.
5. Проверьте двухстороннее неравенство
табл
табл
FF
F
≤≤
1
(F
табл
=28,04 при вероятности отвергнуть
правильную гипотезу p=0,01) и на основании этого сделайте вывод о характере вращательного движения маятника.
6. Вычислите момент инерции маятника и его дисперсию по формулам
A
I
1
>=<
;
2
2
2
1
Ai
S
A
S =
, где
2
4
1
2
2
1
)1(
)(
i
i
ii
A
xn
Axy
S ⋅
−
−
=
∑
=
.
Окончательный результат запишите в виде
><
±>=<
I
SII
Упражнение V.
Изучение зависимости момента инерции от массы и определение моментов инерции кольца
k
I
и
диска держателя
g
I
.
Уравнение вращательного движения маятника имеет следующий вид:
ε
r
r
IM =
. Откуда следует, что
ε
r
r
M
I =
.
Поскольку
r
a
ε
= , то изменяя радиус оси маятника, меняется ускорение поступательного движения. Для дальнейших
расчетов введем следующие обозначения:
i
i
ii
r
a
y ==
ε
;
)(
iii
agmrMx −==
, где
2
2
i
i
t
h
a =
;
I
A
1
= .
1. Изменяя с помощью подвижных втулок радиус оси маятника, проведите замеры времени падения маятника.
Результаты занесите в таблицу 3.4.
Таблица 3.5.
№
i
m
i
t
i
a
i
ε
i
M
i
I
ii
Im
2
i
m
β
α
−
−
ii
mI
2
)(
βα
−−
ii
mI
1
2
3
4
5
∑
—
—
—
—

2. Рассчитайте
i
a ;
i
ε
.;
i
M ;
i
I , данные занесите в таблицу. 3.4.
2
11
2
111
)(
∑∑
∑∑∑
==
===
−
−
=
n
i
i
n
i
i
n
i
i
n
i
i
n
i
ii
mmn
ImImn
α
;
.
)(
2
11
111
2
1
∑∑
∑∑∑∑
==
====
−
−
=
n
i
i
n
i
m
i
n
i
ii
n
i
i
n
i
i
n
i
i
mmn
Immmm
β
3. Определив
α
и
β
, рассчитайте дисперсию адекватности и проверьте адекватность линейной
модели зависимости по
F
-критерию
2
2
I
адк
рас
S
S
F =
,
)1(
)(
2
2
−
−−
=
∑
nn
mI
S
ii
фдк
βα
.
Если
12,9
1
=
′
≤≤
таблрас
FF
F
, гипотеза об адекватности модели не отвергается.
4. Постройте график зависимости
β
α
+
=
mI и, отложив на нем экспериментальные точки,
убедитесь, что они лежат вблизи прямой.
Если последнее равенство выполняется, все расчеты верны и момент инерции кольца любой массы можно
определить из выражения
адкk
SmI ±=
α
.
Контрольные вопросы
1. Дайте определение момента силы, инерции, момента импульса, углового ускорения.
2. Сформулируйте закон вращательного движения твердого тела.
3. Выведите расчетную формулу момента инерции.
4. Составьте ответ на билет программированного контроля.
5. Сформулируйте и докажите теорему Штейнера.
6. Какие величины характеризуют динамику вращательного движения?
7. Как связано ускорение поступательного движения маятника с
его угловым ускорением?
8. Вывести рабочую формулу для определения момента силы реакции нити относительно центра
инерции маятника.
