Масленникова О.Е., Попова И.В. Основы искусственного интеллекта

Подождите немного. Документ загружается.

- 31 -

Суждение

Суждение – это структурно-сложный объект, отражающий

объективную связь между объектом и его свойством.

Суждению противопоставляются такие сущности, как: «предложение»,

«перцепции», «сцены из реального мира».

Пример. Следующие предложения выражают одно и то же суждение:

− «Акула есть хищная рыба»;

− «Все акулы - хищные рыбы».

− «Хищными рыбами являются акулы».

Классическая логика рассматривает структуру простого суждения в

несколько иной интерпретации, чем это принято в современных логико-

лингвистических исследованиях. Так, в соответствии с понятиями

классической логики о структуре суждения, простое суждение есть

абстрактный объект, основными структурными элементами которого

являются:

− индивидный концепт (ИК);

− предикатный концепт (ПК);

− отношение предикации (ОП).

Примеры

Дано предложение: «Платон является философом».

В этом предложении, выражающем суждение S:

«Платон» – это логический субъект, т.е. символ, обозначающий

индивидный концепт суждения S.

«Философ» – это логический предикат, т.е. символ, обозначающий

предикатный концепт суждения S.

«Являться» – субъектно-предикатная связка, т.е. символ,

обозначающий отношение предикации.

Таким образом, можно сделать следующий промежуточный вывод:

− индивидный концепт – это система понятий, рассматриваемая в

качестве понятийной сущности, некоторого эмпирического объекта;

− предикатный концепт – понятие, рассматриваемое в качестве

свойства того или иного конкретного эмпирического объекта;

− отношение предикации – отношение, связывающее индивидный

и предикатный концепты некоторого эмпирического объекта в целостный

абстрактный объект.

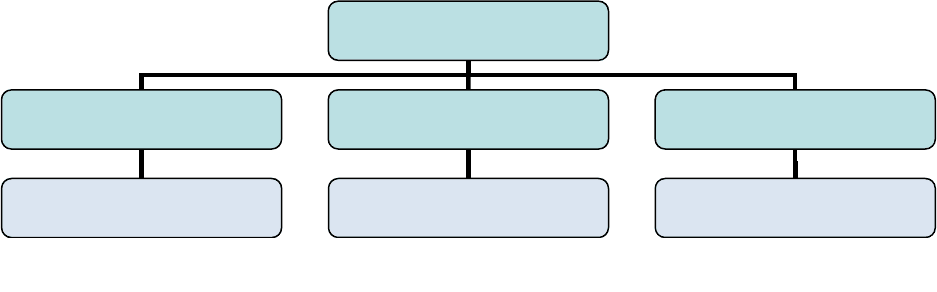
Кроме того, можно выделить несколько типов простых суждений (См

рис. 15).

Существует несколько способов формализации элементарных

суждений.

- 32 -

1-й способ. Естественный язык, который традиционно считается

громоздким и неточным, однако формального способа, который мог бы

сравниться по своей универсальности с естественным языком, до сих пор не

придумано.

2-й способ. Традиционная аристотелевская логика.

3-й способ. Современная символическая логика.

Основные виды сложных суждений

Кроме суждений, выражаемых в аристотелевской логике

высказываниями вида A, E, I, O (см. п. Логика Аристотеля), имеются и

различного рода сложные суждения. Чем сложнее суждение, тем труднее

точно формализовать его средствами традиционной аристотеловской логики,

а в ряде случаев такая формализация просто невозможна. Поэтому анализ

логической структуры сложных суждений целесообразно проводить

средствами современной символической логики и в том числе средствами

логики высказываний и логики предикатов (см. соответствующие пункты

параграфа).

К основным видам сложных суждений относятся

− конъюнктивные;

− дизъюнктивные;

− импликативные;

− модальные:

o алетические (необходимо, возможно, случайно);

o эпистемические ( знаю, верю, полагаю, считаю);

o деонтические (решено, запрешено);

o аксиологические (хорошо, плохо);

o темпоральные (в прошлом, раньше, вчера, завтра, в

будущем);

− вопросы:

o ли- вопросы;

o что- вопросы.

Здесь также наблюдается преемственность классов логики и методов

искусственного интеллекта.

Простые суждения

Атрибутивные

Об отношениях

Существования

Монахи, как правило,

скромны

Магнитогорск южнее

Челябинска

Существуют голубые ели

Рис. 15. Виды простых суждений

- 33 -

Умозаключения

Под умозаключением (в традиционной логике) понимается некая

форма мышления, посредством которой осуществляется умственный переход

(называемый «выводом») от одного или нескольких суждений (называемых

«посылкой») к какому-нибудь другому суждению (называемому

«заключением»).

Таким образом, умозаключение – сложный абстрактный объект, в

котором с помощью определенных отношений объединяется в единое целое

одно или несколько суждений.

Для обозначения умозаключения в логике используется термин

силлогизм.

Силлогизмы бывают формальные и неформальные.

Первые формальные силлогизмы использовал Аристотель.

Разработанная им силлогистика (теория формальных силлогизмов, т.е.

умозаключений) оказала существенное влияние на развитие античной и

схоластичной логики, послужила основой для создания современной

логической теории умозаключений.

Для закрепления понятий логики необходимо выполнить упражнения на

стр. 78.

Законы логики

К числу наиболее важных логических законов относятся:

− тождества (любой объект тождественен лишь самому себе);

− не противоречивости (контрадикторные друг другу высказывания не

могут быть одновременно истинными);

− исключенного третьего (из двух кондрадикторных друг другу

высказываний одно истинно, другое ложно, а третьего не дано);

− достаточного основания (любое истинное высказывание имеет

достаточное основание, в силу которого оно истинно, а не ложно).

Рассмотрим более подробно каждую из обозначенных позиций.

I. Закон тождества

Закон тождества доказывает то, что всякая мысль тождественна самой

себе, «А есть А» (А → А), где А – любая мысль. Например: «Поваренная

соль NaCl состоит из Na и Cl».

При нарушении этого закона возможны ошибки, перечисленные ниже.

Амфиболия (от греческого amphibolos – двусмысленность,

двойственность) – логическая ошибка, в основе которой лежит

двусмысленность языковых выражений. Другое название этой ошибки –

«подмена тезиса».

Пример

«Правильно говорят, что язык до Киева доведет. А я купил вчера

копченый язык. Теперь смело могу идти в Киев».

- 34 -

Эквивокация – логическая ошибка, в основе которой лежит

использование одного и того же слова в разных значениях. Эквивокация

часто используется как художественный риторический прием. В логике этот

прием еще называют «подмена понятия».

Пример

«Старый морской волк – это действительно волк. Все волки живут в

лесу». Здесь ошибка обусловлена тем, что в первом суждении слово «волк»

используется в качестве метафоры, а во второй посылке – в прямом

значении.

Логомахия – спор о словах, когда в процессе дискуссии участники не

могут прийти к единой точке зрения в силу того, что не уточнили исходные

понятия.

Таким образом, закон тождества выражает одно из важнейших

требований логического мышления – определенность.

II. Закон не противоречия

Данный закон выражает требование непротиворечивости мышления.

Закон не противоречия гласит: два суждения, из которых в одном

утверждается нечто о предмете мысли («А есть В»), а в другом тоже самое

отрицается об этом же предмете мысли («А не есть В»), не могут быть

одновременно истинными, если при этом признак В утверждается или

отрицается о предмете мысли А, рассматриваемом в одно и то же время и в

одном и том же отношении.

Например, суждения «Кама – приток Волги» и «Кама не является

притоком Волги» не могут быть одновременно истинными, если эти

суждения относятся к одной и той же реке.

Противоречия не будет, если мы что-либо утверждаем и то же самое

отрицаем относительно одного и того же лица, которое, однако,

рассматривается в разное время.

Так, суждения «Данный человек – студент МаГУ» и «Данный человек –

не является студентом МаГУ» могут быть одновременно истинными, если в

первом из них имеется в виду одно время (когда данный человек учится в

МаГУ), а во втором – другое (когда он закончил университет).

Закон не противоречия указывает на то, что из двух противоположных

суждений одно необходимо ложно. Но поскольку он распространяется и на

противные, и на противоречащие суждения, вопрос о втором суждении

остается открытым: оно не может быть как истинным, так и ложным: бумага

не может быть белой и небелой.

III. Закон исключенного третьего

Закон исключенного третьего утверждает, что два противоречащих

суждения не могут быть одновременно ложными: одно из них необходимо

истинно; другое – необходимо ложно; третье суждение исключено, т.е.

истинно либо А, либо не-А.

- 35 -

Закон исключенного третьего формулирует важное требование к

вашему мышлению: нельзя отклоняться от признания истинным одно из двух

противоречащих друг другу высказываний и искать нечто третье между

ними. Если одно из них признано истинным, то другое необходимо признать

ложным и не искать третье.

Пример: животные могут быть либо позвоночные, либо не

позвоночные, третьего ничего не может быть.

IV. Закон достаточного основания

Содержание данного закона можно выразить следующим образом: для

того, чтобы считаться вполне достоверным, всякое положение должно быть

доказано, т.е. должны быть известны достаточные основания, в силу которых

оно считается истинным.

Достаточным основанием может быть другая, уже проверенная

практикой, признанная истинной мысль, необходимым результатом которой

является истинность доказываемого положения.

Пример. Логическим обоснованием суждения «В комнате стало

теплее» является факт расширения ртути термометра. В науке

достаточными основаниями считаются: а) положения об удостоверенных

фактах действительности, б) научные определения, в) ранее доказанные

научные положения, г) аксиомы, а также д) личный опыт.

Логический вывод

Логический вывод - это получение некоторой формулы исходя из

множества других логических формул путѐм применения правил вывода.

Интерпретатор логических выражений, пользуясь логическим выводом,

сам строит необходимую цепочку вычислений на основе исходного

описания. Значение логического подхода заключается в возможности

построения интерпретатора, работа которого не зависит от логических

формул. Правила в логическом представлении имеют вид: P

←P

, …, P

. Р

называют целью, а Р

, Р

, ..., Р

- телом правила. Предикаты Р

, Р

, ..., Р

условия, которые должны быть выполнены, чтобы достижение цели Р

стало

успешным.

Разберѐм основы логического вывода на примере выполнения

процедуры определения правильности рассуждения.

Определение логически правильного рассуждения

Когда мы говорим, что одно предложение D логически следует из

другого Р, то имеем в виду следующее: всякий раз, когда предложение Р

истинно, то истинно и предложение D. В логике высказываний мы имеем

дело с формулами Р и D, зависящими от некоторых переменных X

, X

,.., Х

Определение. Будем говорить, что из формулы Р(Х

, Х

,...,Х

)

логически следует формула D(Х

, Х

,...,Х

) и обозначать Р├ D, если для

- 36 -

любых наборов значений Х

, Х

,...,Х

при условии Р(Х

, Х

,...,Х

) = И

выполняется условие D(Х

, Х

,...,Х

) = И .

Формула Р называется посылкой, a D - заключением логического

рассуждения.

Обычно в логических рассуждениях используется не одна посылка Р, а

несколько; в этом случае рассуждение будет логически правильным из

конъюнкции посылок логически следует заключение.

Проверка правильности логического рассуждения

Первый способ – по определению:

a) записать все посылки и заключения в виде формул логики

высказываний;

b) составить конъюнкцию формализованных посылок Р

& P

&…&

c) проверить по таблице истинности, следует ли заключение D из

формулы Р

&Р

&...&Р

Второй способ основан на следующем признаке логического

следования: «Формула D логически следует из формулы Р тогда и только

тогда, когда формула Р |- D является тавтологией». Тогда проверка

правильности логического рассуждения сводится к ответу на вопрос:

является ли формула тавтологией? На этот вопрос можно ответить, построив

таблицу истинности для формулы, или сведя эту формулу с помощью

равносильных преобразований к известной тавтологии.

Третий способ проверки правильности логического рассуждения

назовем сокращенным, т.к. он не требует полного перебора значений

переменных для построения таблицы истинности. Для обоснования этого

способа сформулируем условие, при котором логическое рассуждение

является неправильным. Рассуждение является неправильным, если

найдется набор значений переменных

, X

,.., Х

такой, что посылка

, X

,.., Х

)=Л

, а заключение

, X

,.., Х

)=И.

Пример.

Дано рассуждение: «Если идет дождь, то кошка в комнате или в

подвале. Мышка в комнате или в норке. Если кошка в подвале, то мышка в

комнате. Если кошка в комнате, то мышка в норке, а сыр в холодильнике.

Сейчас идет дождь, а сыр лежит на столе. Где кошка и где мышка?».

Введѐм следующие обозначения: Д – «идет дождь»; К – «кошка в

комнате»; Р – «кошка в подвале»; М – «мышка в комнате»; Н – «мышка в

норке»; Х – «'сыр в холодильнике»; ¬Х – «сыр на столе». Получаем

следующую схему рассуждения:

Д→К|Р

М|Н

К→Н&Х

Истинно

Ложно

- 37 -

Р→М

Д&¬Х

-----

Воспользуемся правилами вывода

1) Д&¬Х├Д;

2) Д&¬Х├¬Х;

3) Д→К|Р, Д├ К|Р.

Далее рассмотрим два варианта.

Вариант А. Пусть имеет место К. Тогда

4а) К, К→Н&Х, К├ Н&Х;

5а) Н&Х ├ Х;

6а) ¬Х,Х├Х&¬Х –

получили противоречие, значит, предположение было ошибочно

и этот вариант невозможен.

Вариант Б, Пусть имеет место Р. Тогда

4б) Р, Р →М├М;

5б) Р,М├Р&М

Получено заключение Р&М, т.е. «кошка в подвале, а мышка в

комнате»

Пример

Проверить правильность рассуждения сокращенным способом.

Какими еще способами можно решить эту задачу?

Дано рассуждение: «Если сегодня будет мороз, то я пойду на каток.

Если сегодня будет оттепель, то я пойду на дискотеку. Сегодня будет мороз

или оттепель. Следовательно, я пойду на дискотеку».

Решение. Формализуем условие задачи, введя обозначения:

М – «сегодня будет мороз»;

К – «я пойду на каток»;

О – «сегодня будет оттепель»;

Д – «я пойду на дискотеку».

Схема рассуждения имеет вид:

M → K

O → Д

M | O

----

Рассуждение является логически правильным, если при любых

наборах значений переменных (M, К, О, Д), дня которых все посылки,

истинны, заключение также истинно. Предположим противное: есть набор

.Д

) такой, что посылки истинны, а заключение ложно. Применяя

определения логических операций, попытаемся найти этот набор.

Убеждаемся, что предположение справедливо при значениях переменных

- 38 -

М0 =И, К0 =И, О0 = Л, Д0 = Л ( табл. 1). Следовательно, рассуждение не

является логически правильным.

Таблица 1

Схема решения логической задачи

№

Истина

Ложь

Примечания

→K

→Д

˅ O

предполагаем, что посылки

истинны,

а заключение ложно

из 2,4 и определения импликации

из 3, 5 и определения дизъюнкции

из 1, 6 и определения импликации

Другой способ решения задачи: построить таблицу истинности для

формулы (М→К)&(О→Д)&(M˅O) →Д и убедиться, что она не является

тавтологией. Тогда по признаку логического следования рассуждение не

является логически правильным. Так как в рассуждении участвуют четыре

высказывательные переменные (M, К, О, Д), то таблица истинности будет

содержать 16 строк, и этот способ является трудоѐмким.

С помощью правил вывода можно построить логически правильное

рассуждение, но не всегда можно доказать неправильность логического

рассуждения. Поэтому для данной задачи наиболее удобным является

сокращенный способ проверки правильности логического рассуждения.

Для закрепления правил логического вывода необходимо выполнить

упражнения на стр. 78.

Основные разделы современной символической логики

В развитии классической логики выделяют три следующих основных

этапа: античная логика (около 500 до н.э. - нач. н. э.), схоластическая логика

(нач. н. э. - первая пол. XIX века), современная символическая логика (сер.

XIX-XX вв.)

Современная символическая логика подразделяется на основные

разделы, суть которых раскрыта ниже.

Логика высказываний (исчисление высказываний). Изучает

простые суждения, рассматриваемые без учета их внутренней структуры, а

также элементарные умозаключения наиболее доступные человеческому

пониманию. В естественном языке такие простые суждения представлены

предложениями, которые рассматриваются лишь с точки зрения их

истинности или ложности, а умозаключения - соответствующими системами

высказываний.

- 39 -

Логика предикатов (исчисление предикатов). Более сложными

объектами исследования являются суждения, рассматриваемые с учетом их

внутренней структуры. Раздел логики, в котором изучаются не только связи

между суждениями, но и внутренняя понятийная структура суждений,

получил название «логика предикатов».

Металогика. Металогика представляет собой расширение логики

предикатов. Предметом ее изучения является вся сфера отношений в целом,

все те универсальные отношения, которые могут иметь место между

понятиями, суждениями, умозаключениями, а также символами, их

обозначающими.

В следующих пунктах параграфа представлены ключевые позиции

логики высказываний и предикатов первого порядка. В целях лучшего

понимания современных логик, необходимо рассмотреть основные

положения, определяемые силлогизмами Аристотеля.

Логика Аристотеля

В логике Аристотеля строение элементарных суждений выражают

структуры:

− S есть P (1);

− S не есть P (2) , где S – некоторый логический субъект (от лат.

Subjectum); P - некоторый логический предикат (от лат. Predicatum).

Виды суждений логики Аристотеля перечислены ниже.

1. Общеутвердительные суждения – А

«Все S есть Р» – Все поэты впечатлительные люди.

Слова «есть», «не есть» выполняют роль субъектно-предикатной

связки. Из высказываний (1) и (2) с помощью слов «все» и «некоторые»

строятся высказывания вида:

− все S есть P : Тип A (Affirmo);

− некоторые S есть P : Тип I (AffIrmo);

− все S не есть P : Тип N (Nego);

− некоторые S не есть P : Тип O (NegO).

2. Общеотрицательные суждения – Е (N)

«Ни одно S не есть Р» - Ни один человек не всеведущ.

3. Частноутвердительное суждение – I

«Некоторые S есть Р» – Некоторые люди имеют курчавые волосы.

4. Частноотрицательное суждение – О

«Некоторые S не есть Р» – Некоторые люди не умеют слушать.

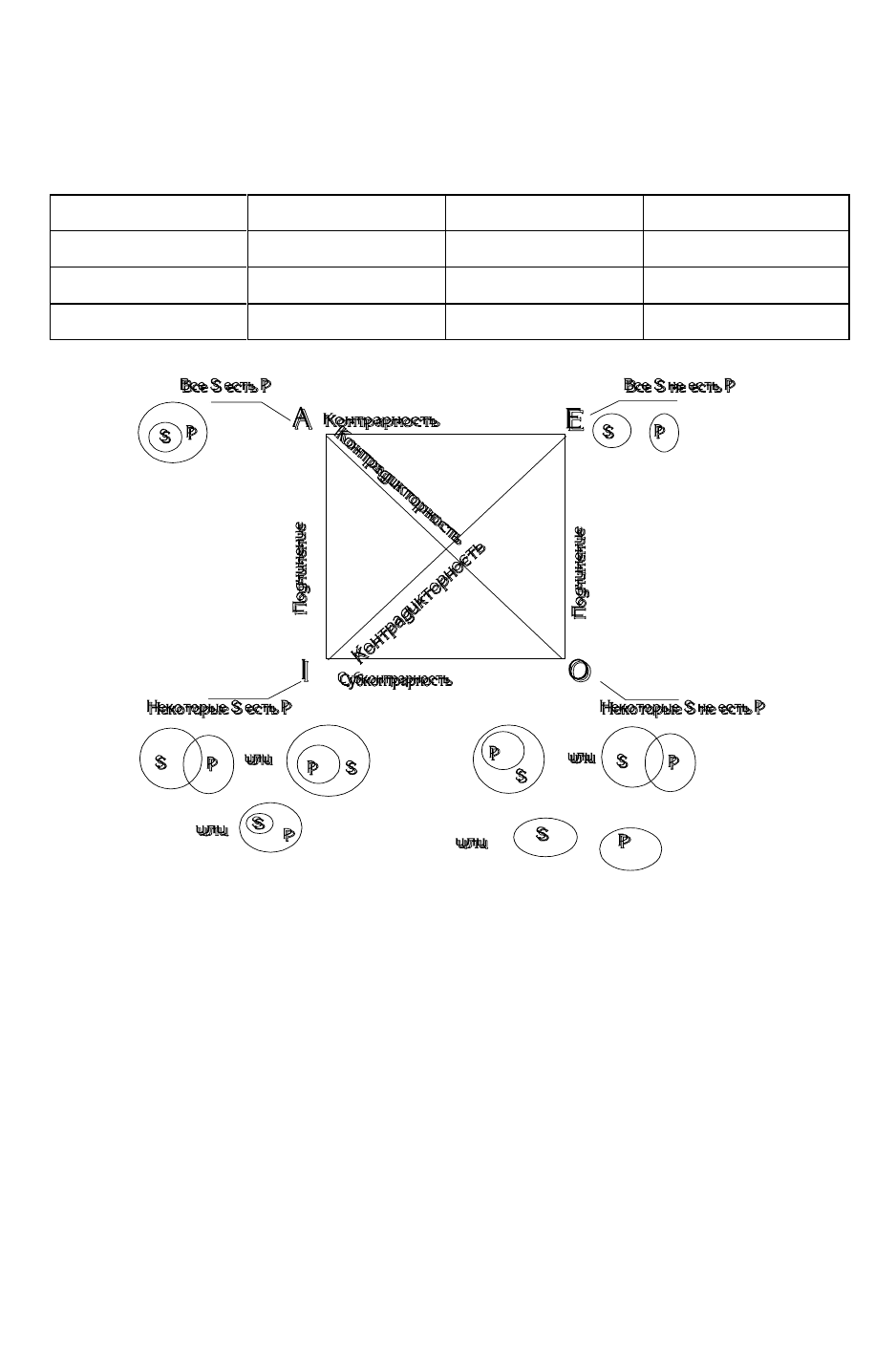
Высказывания типа A, E, I, O суть простые категорические

высказывания, образующие фундамент всей аристотелевской логики. Между

истинностью и ложностью высказываний типа A, E, I, O имеет место

функционально-целостные отношения, которые обычно изображают в виде

логического квадрата (рис. 16, табл. 2).

- 40 -

При использовании логического квадрата важно учитывать следующую

тонкость: слово «некоторые» при этом понимается в широком смысле – как

«некоторые, а может быть и все».

Таблица 2

Таблица истинности для суждений логики Аристотеля

Рис. 16. Логический квадрат

Пояснения к логическому квадрату Аристотеля

В левом верхнем углу логического квадрата располагаются

высказывания типа A (общеутвердительные).

В правом верхнем углу – высказывания типа E (общеотрицательные).

В левом нижнем углу (под A) – высказывания типа I

(частноутвердительные).

В правом нижнем углу (под E) – высказывания типа O

(частноотрицательные).

Высказывания типов А и О, а также высказывания типов Е и I

находятся между собой в отношении контрадикторности, или противоречия

(диагональные отношения).

Высказывания типов А и Е находятся в отношении контрарности, или

противоположности.