Масленникова О.Е., Попова И.В. Основы искусственного интеллекта

Подождите немного. Документ загружается.

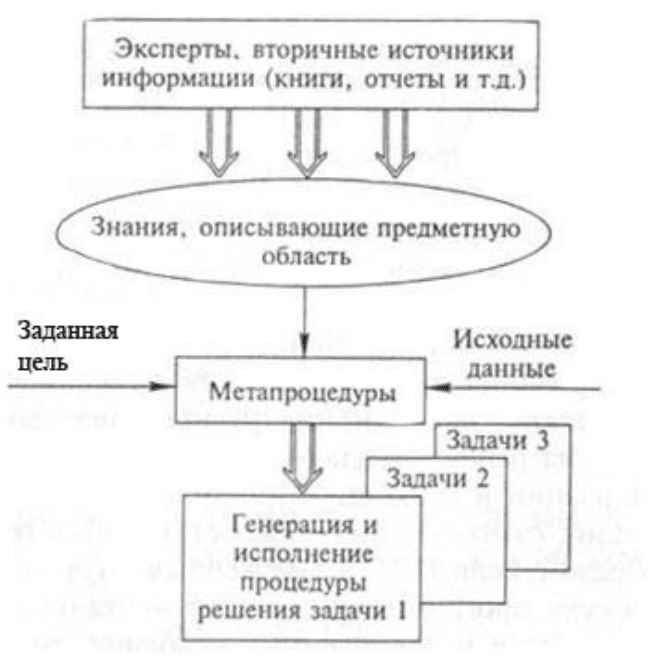
- 131 -

исходных данных мета-процедуры системы генерируют и исполняют

процедуру решения конкретной задачи.

Данную технологию называют технологией систем, основанных на

знании, или технологией инженерии знаний.

Рис. 60. Технология использования ИнС общего назначения

(инженерия знаний)

К специализированным ИнС отнесены те, которые выполняют решение

фиксированного набора задач, предопределенного при проектировании

системы. Для использования таких систем требуется наполнить их данными,

соответствующими выбранному приложению (прикладным задачам,

предметной области). Примерами специализированных ИнС являются,

например, интеллектуальные диалоговые системы, а также прикладные ЭС.

Так как терминология в области разработки ИнС находится на стадии

формирования, определим основные термины следующим образом

Экспертная система (система, основанная на знаниях, — СОЗ) -

сложный программный комплекс, аккумулирующий в формальном виде

знания специалистов в конкретных предметных областях.

Пользователь - лицо, для которого предназначена система.

Инженер по знаниям (когнитолог, инженер-интерпретатор) -

специалист по ИИ, выступающий в роли промежуточного буфера между

экспертом и базой знаний.

- 132 -

Эксперт - высококвалифицированный специалист, согласившийся

поделиться опытом в рассматриваемой предметной области. Интерфейс

пользователя — комплекс программ, реализующих диалог пользователям с

ИнС на всех стадиях функционирования ИнС.

База знаний (БЗ) - ядро ИнС, совокупность знаний предметной

области, записанная на машинный носитель на языке представления знаний

(обычно приближенном к естественному).

Решатель (машина логического вывода, дедуктивная машина,

интерпретатор) - программа, моделирующая ход рассуждений эксперта на

основании знаний, имеющихся в БЗ.

Подсистема объяснений - программа, позволяющая пользователю

получать ответы на вопросы: как была получена та или иная рекомендация и

почему система приняла такое решение?

Технология синтеза ЭС - технология создания на основе знаний

экспертов систем, решающих неформализованные задачи в

слабоструктурированных предметных областях.

В общем случае все ИнС можно подразделить на решающие задачи

анализа и на решающие задачи синтеза. Примерами задач анализа являются

задачи интерпретации данных и диагностики. Примерами задач синтеза

являются задачи проектирования и планирования. Комбинированные задачи -

задачи обучения, мониторинга, управления.

Следует отметить, что подавляющее число ИнС, используемых для

решения практически значимых задач, являются интегрированными, т.е.

состоящими из традиционной ИнС и других программных систем, с

которыми ИнС взаимодействуют в процессе работы (СУБД, пакеты

прикладных программ (ППП), электронные таблицы и т.д.).

Сферы применения интеллектуальных информационных систем

1. Представление знаний. В рамках этой проблемы решаются

задачи, связанные с формализацией и представлением знаний в памяти ИнС.

Для этого разрабатываются специальные модели представления знаний и

языки для описания знаний, выделяются различные типы знаний. Изучаются

источники, из которых ИнС может черпать знания, и создаются процедуры и

приемы, с помощью которых возможно приобретение знаний для ИнС.

2. Манипулирование знаниями. Для того чтобы знаниями можно

было пользоваться при решении задач, ИнС должна уметь:

1) оперировать знаниями;

2) пополнять знания (с помощью разрабатываемых способов на

основе неполного описания знаний);

3) классифицировать хранящиеся в системе знания;

4) обобщать по тем или иным разработанным процедурам знания;

5) формировать на основе знаний абстрактные понятия;

6) осуществлять достоверный и правдоподобный вывод на основе

имеющихся знаний с помощью создаваемых методов;

- 133 -

7) пользоваться моделями рассуждений, имитирующими

особенности человеческих рассуждений.

3. Общение. На основе исследований в этом направлении

формируются методы построения лингвистических процессоров (ЛП),

вопросно-ответных систем (ВОС), диалоговых систем (ДС) и других ИнС,

целью которых является обеспечение комфортных условий для общения

человека с ИнС.

4. Восприятие. Это направление включает проблемы анализа

трехмерных сцен; разработку методов представления информации о

зрительных образах в базе знаний; создание методов перехода от

зрительских сцен к их текстовому описанию и методов обработки

перехода; разработку процедур когнитивной графики (КГ); создание

средств для порождения зрительских сцен на основе внутренних

представлений в ИнС.

Существуют большие возможности в повышении уровня

интеллектуальности ИнС за счет обработки зрительной (образной)

информации и соотнесения ее с обработкой символьной (текстовой)

информации.

5. Обучение. Основная черта ИнС — это способность к обучению,

т.е. решение задач, с которыми они ранее не встречались.

6. Поведение. Так как ИнС должны действовать в некоторой

окружающей среде, то необходимо разработать специальные поведенческие

процедуры (бихевиористические модели), которые позволили бы им

адекватно взаимодействовать с окружающей средой, другими ИнС и

людьми. Для достижения такого взаимодействия необходимо вести

исследования в ряде направлений и создать модели целесообразного

поведения, нормативного поведения, ситуационного поведения,

специальные методы многоуровневого планирования и коррекции планов в

динамических ситуациях.

- 134 -

Рис. 61. Схема системного анализа проблемной области

на применимость технологии ЭС

- 135 -

Упражнения

1. Для каждой предметной области выполните постановку задачи;

выделите и заполните значениями атрибуты, реализуйте стратегию поиска

решения, диалоговые окна с пояснениями и оформите вывод (допустимо

использовать процедуры, переменные и константы):

а) разработать макет экспертной системы при помощи

программных средств XpertRule, реализующий структуру правил базы

знаний для формирования заявки на программное обеспечение

учебного класса для отдельной образовательной программы;

б) разработать макет экспертной системы при помощи

программных средств XpertRule, реализующий структуру правил базы

знаний для подбора персонала школы. По результатам тестирования

система должна определить, подходит ли данная кандидатура на

желаемую должность, и/или предложить наиболее подходящую;

в) Разработать макет экспертной системы при помощи

программных средств XpertRule, реализующий структуру правил базы

знаний, построенной на основе данных об учебной программе

общеобразовательной школы. Для каждой книги известны автор,

тематика, предмет. Система должна предложить сформировать набор

учебной литературы для школьника;

г) Разработать макет экспертной системы при помощи

программных средств XpertRule, позволяющей оценить знания

школьника по отдельной дисциплине.

Таблица 14

Методы построения задачи

Номер

метода

Шаг 1

Шаг 2

Шаг 3

Результат

Определить

атрибуты

Ввести примеры

Получить

дерево

решений

Дерево

решений

Определить

атрибуты

Ввести дерево

исключений

Получить

дерево

решений

Дерево

решений

Определить

атрибуты

Ввести дерево

решений

Дерево

решений

Определить

атрибуты

Ввести правила

продукции

Правила

продукции

- 136 -

Таблица 15

Распределение вариантов

Номер

варианта

Метод

построения

задачи

Способ формирования цепочек

Задача

Прямое построение цепочки

Обратное построение цепочки

Вопросы для самоконтроля

1. Какие знания относят к формализованным? Приведите примеры.

2. Какие знания относят к неформализованным? Приведите примеры.

3. Каковы основные признаки экспертных систем?

4. Сформулируйте причины, которые способствуют распространению

ЭС?

5. Каково назначение ЭС?

6. На основе материала параграфа, сформулируйте определение

экспертной системы.

7. По каким критериям можно охарактеризовать любую ЭС?

- 137 -

8. Что необходимо определить для ЭС, чтобы сформулировать еѐ

назначение?

9. Какие типы задач решает ЭС с точек зрения разработчика и

пользователя?

10. Охарактеризуйте статическую ЭС.

11. Охарактеризуйте динамическую ЭС.

12. Как определить степень сложности и степень связанности решаемой

задачи? Как это влияет на характеристику ЭС?

13. Как определить пространство поиска и количество активных агентов

решаемой задачи? Как это влияет на характеристику ЭС?

14. Охарактеризуйте ЭС по классу решаемых задач, используя

следующие аспекты: задачи расширения, доопределения,

преобразования.

15. Приведите краткую характеристику глубинных и поверхностных ЭС.

16. Приведите краткую сравнительную характеристику традиционных и

гибридных ЭС.

17. Какие поколения ЭС Вы знаете, приведите их комплексную

характеристику.

18. Какие ЭМ по технологии проектирования называют простыми, а

какие – сложными?

19. Разведите понятия демонстрационный, исследовательский и

действующий прототипы ЭС?

20. В каких областях науки и техники получили своѐ наибольшее

распространение ЭС? Приведите примеры.

21. Охарактеризуйте круг задач, решаемых с помощью ЭС, в медицине?

22. Чем определяется сложность разработки ЭС?

23. Какие этапы разработки экспертной системы Вы знаете?

24. Поставьте соответствие между этапами разработки ЭС, ролью

инженера по знаниям и эксперта в каждом из них.

25. В чѐм суть прототипной технологии разработки ЭС?

26. Поставьте соответствие между этапами разработки ЭС видами

прототипов, которые в их ходе формируются?

27. Представьте краткую характеристику этапа идентификации.

28. Представьте краткую характеристику этапа концептуализации.

29. Сформулируйте признаки, по которым можно судить, что этапы

идентификации концептуализации закончены и можно переходить

на следующий этап разработки ЭС.

30. Представьте краткую характеристику этапа формализации.

31. Представьте краткую характеристику этапа выполнения или

реализации БЗ.

32. Представьте краткую характеристику этапа тестирования.

33. Представьте краткую характеристику этапа опытной эксплуатации.

34. Как Вы считаете, когда может быть закончен этап тестирования?

35. Какое место в жизненном цикле ЭС занимает модификация?

- 138 -

36. Можно ли считать модификацию отдельным этапом разработки ЭС?

Ответ обосновать.

37. Из каких основных компонентов состоит ЭС? Укажите назначение

каждого из них.

38. Объясните роль базы знаний и рабочей памяти в работе ЭС.

39. Поясните алгоритм работы экспертной системы в режиме

«консультации».

40. Составьте таблицу соответствия «режим работы с ЭС» - «кто

взаимодействует с ЭС» - «компонент ЭС, участвующий в работе».

41. Приведите краткую характеристику существующих классов

программных инструментальных средств ЭС.

42. На основе предложенного алгоритма выбора инструментальных

средств ЭС, сформулируйте свой алгоритм.

43. Проведите сравнительных анализ такого типа инструментальных

средств ЭС как оболочка:

a. подберите 3-5 названий оболочек;

b. выделите не менее 5 критериев для сравнительного анализа;

c. результаты анализа оформите в виде таблицы.

44. Разработайте макет экспертной системы, согласно варианту задания

на самостоятельную работу.

Литература

1. Гаскаров, Д. В. Интеллектуальные информационные системы :

учебник для вузов / Д.В. Гаскаров. – М.: Высшая школа, 2003 . – 431 с.

2. Конспект лекций «Введение в экспертные системы». - Режим

доступа: http://www.zubolom.ru/lectures/iis/10.shtml

3. Конспект лекций по дисциплине «Интеллектуальные

информационные системы». – Режим доступа: http://sapr.mgsu.ru/biblio/ex-

syst/Glava17/Index1.htm

4. Курс лекций по дисциплине «Системы искусственного

интеллекта». - Режим доступа: http://www.mari-el.ru/mmlab/home/AI/7_8/

5. Современные экспертные системы. – Режим доступа:

http://www.homerobotics.ru/soft_3.asp

6. Тельнов, Ю.Ф. Интеллектуальные информационные системы :

учеб. пособие / Ю.Ф. Тельнов. – М.: Московский международный институт

эконометрики, информатики, финансов и права, 2002. – 118 с.

- 139 -

ГЛАВА 4. ПРОЛОГ КАК ЯЗЫК ЛОГИЧЕСКОГО

ПРОГРАММИРОВАНИЯ

4.1. Представление о логическом программировании

Логическое программирование – это один из подходов к

информатике, при котором в качестве языка высокого уровня используется

логика предикатов первого порядка в форме фраз Хорна. Это универсальный

абстрактный язык предназначенный для представления знаний и решения

задач. Его можно рассматривать как общую теорию отношений. Логическое

программирование базируется на подмножестве логики предикатов первого

порядка

, при этом оно одинаково широко с ней по сфере охвата.

Логическое программирование даѐт возможность программисту

описывать ситуацию при помощи формул логики предикатов, а затем, для

выполнения выводов из этих формул, применить автоматический решатель

задач (т.е. некоторую процедуру).

При использовании языка логического программирования основное

внимание уделяется описанию структуры прикладной задачи, а не выработке

предписаний компьютеру о том, что ему следует делать. Другие понятия

информатики из таких областей, как теория реляционных баз данных,

программная инженерия и представление знаний, также можно описать (и,

следовательно, реализовать) с помощью логических программ.

После того, как была открыта вычислимость логических следствий в

абстрактном смысле, возникло естественное желание автоматизировать

процесс доказательства при помощи компьютера. Полная логика предикатов

– это язык, обладающий богатыми выразительными средствами. Если

попытаться в общем виде реализовать на компьютере процедуры

доказательства, разработанные для исчисления предикатов, то возникнет

проблема комбинаторного роста числа вариантов. В конце 50-х - начале 60-х

гг. учѐные приступили к поиску таких приемлемых с точки зрения объѐма

вычислений методов реализации процедур доказательства, которые в

максимально возможной степени сохранили бы выразительную силу логики

предикатов первого порядка. У специалистов зародилась мечта о создании на

практике универсальной машины – «решателя задач», которую задумал еще

Лейбниц.

В конце 50-х годов Гилмор, Дэвис, Патнэм и Правиц начали работу по

созданию автоматизированного метода доказательства через опровержение.

За основу был взят метод, разработанный Хербрандом в 30-е годы.

Основываясь на работе Правица, Робинсон создал правило вывода, которое

он назвал резолюцией. Это правило пригодно для выполнения вывода

машиной. Первоначально попытки создания алгоритма решения задач,

базирующегося на резолюции, оказывались успешными только для очень

небольших задач. Лавленд, Ковальски усовершенствовали такие алгоритмы,

см. пункт Логические модели представления знаний

- 140 -

разработав метод устранения моделей и метод селектирующей функции. В

начале 70-х гг. Кольмерор и Руссель воспользовались результатами этих

работ при создании языка, базирующегося на правиле резолюции. Этот язык

они назвали Пролог - Программирование при помощи ЛОГики [93].

Области применения логического программирования:

− разработка быстрых прототипов прикладных программ;

− управление производственными процессами;

− перевод с одного языка на другой;

− разработка компиляторов;

− решение задач теории графов;

− создание естественно-языковых интерфейсов для существующих

систем;

− реализация экспертных систем (ЭС) и оболочек ЭС;

− доказательство теорем и пакеты искусственного интеллекта, в

которых возможности языков логического программирования,

например Пролога, по обеспечению дедуктивного вывода

применяются для проверки различных теорий.

Языки логического программирования не предназначены для

написания программ, обрабатывающих большой объем арифметических

вычислений (обработка аудио, видео и т.д.), а также для написания

драйверов.

Таким образом, логическое программирование представляет собой

нетрадиционную технологию программирования. Оно основано на идеи

описания задачи совокупных утверждений, в некотором формальном

логическом языке и получение решения задачи построением вывода в

формальной дедуктивной системе.

Одним из наиболее распространѐнных языков логического

программирования по праву считается Пролог. Дальнейшее изучение основ

данного типа программирования будет осуществляться именно на его основе.

4.2. Представление знаний о предметной области виде

фактов и правил базы знаний Пролога

В Прологе (Prolog – PROgramming LOGic) вы получаете решение

задачи логическим выводом из ранее известных положений. Обычно

программа на Прологе не является последовательностью действий, – она

представляет собой набор фактов и правил, обеспечивающими получение

заключений на основе этих фактов.

При программировании на Прологе усилия программиста направлены

на описание логической модели фрагмента предметной области решаемой

задачи в терминах объектов предметной области, их свойств и отношений

между собой, а не деталей программной реализации.

Фактически Пролог представляет собой не столько язык для

программирования, сколько язык для описания данных и логики их

обработки. Программа на Прологе не является таковой в классическом