Марисова О.И. Трикотажные рисунчатые переплетения

Подождите немного. Документ загружается.

Как известно, восхождение для одной системы определяется

по формуле

li(y+l)-l

X =

Умножив обе части уравнения на п, получим уравнение для оп-

ределения восхождения х, когда раппорт вырабатывается на

машине с числом петле-

образующих систем п: Системы

Сенции Системь.

nh (у h \) —

ХП =

ИЛИ

Х =

Н(у+\)~п

й ш

Г Е

и 1

Ш I ш

I п

Z I I

а 1 а

I ш

5 П

1 ш

а:

л I ш

I Y

I ш

I я

1 / / 1

иг по

гчигпа

игла

Рис. 26. Схема закрепления систем и сек-

ций за рядами раппорта рисунка

Зависимость между но-

мером секции k и номе-

ром ряда q находится для

одной системы по фор-

муле

При многосистемном

вязании возможно полу-

чение сложных рисунков

также в тех случаях, ко-

гда число игл игольницы

N делится без остатка на число делений узороо^разователя Р,

и игольное уравнение имеет вид

N^^Pz.

Известно, что при многосистемном вязании группа игл, рав-

ная ширине раппорта, последовательно работает с одноимен-

ными секциями всех систем.

Допустим, что число систем «=12, ширина раппорта 6 = 24

петли, тогда группа игл с I по 24 проработает сначала с сек-

циями / всех 12 систем, затем с секциями //, III и т. д. На

рис. 26 показана схема закрепления систем и секций за ря-

дами раппорта. Из рисунка видно, что на протяжении 12 рядов

номер секции постоянный, а номер системы переменный, что

позволяет изменять условия чередования гладких и рисунчатых

делений в секциях. Таким образом, возможная высота раппорта

и равна числу п систем на машине.

Я = м,

Из рисунка также видно, что раппорт А начинается сек-

цией /, раппорт 5 —секцией II, раппорт Б —секцией III, рап-

порт Г —секцией II. Все эти секции провязывают ряды 1 рап-

порта, следовательно, они должны иметь одинаковое чередова-

ние гладких и рисунчатых полос.

Отсюда ясно, что чередование гладких и рисунчатых полос

во всех секциях системы I принимается одинаковым и устанав-

ливается в соответствии с чередованием гладких и рисунчатых

петель ряда 1 раппорта. В системе II все секции набираются по

ряду 2 раппорта и т. д.

Таким образом, применение подобной схемы образования

сложных рисунков целесообразно только на машинах с боль-

шим числом систем, так как последнее определяет высоту рап-

порта рисунка.

По указанному способу получают рисунки на жаккардовых

машинах «0Д21». Примеры расчета таких рисунков приведены

ниже в главе ХП.

ПРИМЕРЫ РАСЧЕТА РИСУНКОВ

Перед специалистами могут быть поставлены две задачи.

Задача I. Задан образец полотна с определенным рисунком.

Необходимо осуществить получение подобного рисунка на

имеющемся оборудовании.

Решение. 1. По образцу полотна определим границы рап-

порта рисунка. Подсчитаем ширину, высоту раппорта и вос-

хождение. Допустим, что 6 = 24 петли, Я = 20 рядов, Z = 8 рядов.

2. Определим число систем п. Известно, что Х=хп, H = hn,

следовательно, число систем п есть наибольший общий дели-

тель между величинами X и Н. Х=8, Я=20, поэтому наиболь-

ший общий делитель равен 4 и

/г

= 4.

3. Найдем высоту раппорта h и восхождение л; для одной

системы

= Я:п = 20:4 = 5;

х = Х:п = 8:4 = 2.

4. Найдем боковой сдвиг М для одной системы при у = 0

М _/t(l+у)-1 ^5(1+ 0)-1 _ 4

л; 2 2"

5. Найдем номер секции для каждого ряда раппорта одной

системы.

Номер секции

1 С)

Номер ряда

I + М = 1 + 2 = 3 (1П)

1+2 M = 1 + 4 = 5(V;

1 -f 3

уМ

— 5=1+6-5 = 2 (II)

11-4

8-5 = 4 (IV)

6. Составим таблицу закрепления рядов раппорта за пет-

леобразующими системами и секциями узорообразователя

(табл. 7).

Таблица 7

Номера

систем

Номера секций для каждой

системы

Номера

систем

III

V II IV

/ 1 5

13 17

2 6

III

11 15

8 12

7. Определим периметр узорообразователя

р = Аг, = 24-5 = 120 делений.

8. Определим число игл в игольнице машины из игольного

уравнения.

Значение целого числа z выбирают таким образом, чтобы

расчетное число игл N соответствовало данным каталогов на

оборудование или технической характеристике машины.

Допустим, что по технической характеристике машины МТ22

класса N

—

770 игл, тогда при М=2 и 6=24 наибольшее значе-

ние 2 =

Определим число игл машины при 2 = 6:

Л^

= Pz + Мб = 720 + 48 = 768 игл.

При установке игл в цилиндре машины МТ допускается от-

клонение их числа на 2% в сторону уменьшения, поэтому можно

принять для осуществления заданного рисунка число N, рав-

ным 768.

Задача П. Задана характеристика машины: тип — МТ,

класс—22, диаметр цилиндра —475 мм, число игл —864, пери-

метр узорообразователя — 120 делений, число петлеобразующих

систем — 4. Необходимо спроектировать рисунок прессового пе-

реплетения.

Решение. Прежде всего определим возможность получе-

ния сложного рисунка при заданной характеристике машины по

игольному уравнению

N = Pz + Mb,

Mb = г.

При делении числа игл на число делений узорообразователя

z =

и остается остаток /-=24, следовательно, получение слож-

ного рисунка возможно, Далее приступим к расчету.

1. Определим границы раппорта. Для нахождения ширины

раппорта b разложим числа Я и Р на элементарные множители.

864 2 120 2

432 2 60 2

216 2 30 2

108 2 15 3

54 2 5 5

27 3 1

9 3

3 3

Общие множители —2, 2, 2, 3. Определим возможные ши-

рины раппортов: bi=2\ 62=2-2 = 4; 6з = 2-2-2 =

6„акс =

=2-2-2-3 = 24.

При выборе границ раппорта нужно стремиться к тому, что-

бы прямоугольник, в который вписывается рисунок, прибли-

жался к квадрату, тогда легче проектировать фигуру рисунка.

Примем ширину b равной 24 петлям, тогда высота раппорта

одной системы

/г = Р : 6 = 120: 24 = 5 рядов

и общая высота раппорта

Я = /in = 5-4 = 20 рядов.

Итак, границы раппорта: 6 = 24 петли, Я = 20 рядов.

2. Определим восхождение раппорта X и боковой сдвиг М.

Боковой сдвиг рассчитывается

М=-.г-.Ь,

а так как остаток г = 24 иглы, ширина раппорта Ь=24 петли,

то М = 1.

Восхождение X определяется по формуле

Н(\ \ у)^п

М •

Примем

г/

= 0; тогда при М=1 и Я = 20 восхождение Х=19.

3. Начертим на клетчатой бумаге границы двух соседних

раппортов, условно принимая площадь одной клетки, равной

площади одной петли, и впишем в них фигуры рисунка, т. е.

построим патрон (рис. 27).

4. Определим номера секций узорообразователя для каж-

дого ряда раппорта одной системы при /i = 5 рядов.

Номер ряда Номер секции

1 1 (1)

2 1 +

= 1 + 1 = 2 (И)

3 1+2М = 1+ 2 = 3 (III)

4 1 +3 уИ = 1+3 = 4 С/к;

5 1 + 4 M = 1 + 4 = 5 (V)

5. Составим таблицу закрепления рядов раппорта рисунка

за петлеобразующими системами и секциями узорообразователя

(табл. 8).

Направление образования петель

Рис. 27. Патрон рисунка

6. Составим карту нарезки прессов. По патрону находим,

что образование петель рисунка происходит только в четных

рядах, т. е. системах 11 и /V; в системах I и III устанавли-

ваются обычные прессы. Карту нарезки прессов составляем для

системы II и IV. Образец карты представлен табл. 9.

Номера

систем

III

Таблица 8

Номера секций для каждой системы

JII

Таблица 9

Номера

Последовательность чередования гладких Г и рисунчатых Р

делений в секциях узорообразователя

£S

// I

III

В табл. 9 первые три графы заполняются на основании

табл. 8.

Чередование гладких и рисунчатых делений определяется по

соответствующим рядам рисунка в направлении образования

петель.

Сумма гладких и рисунчатых делений в каждой секции

должна равняться ширине раппорта рисунка. Для нашего при-

мера &=24 петли; поэтому суммарное число делений в каждой

секции также равно 24.

Выше был рассмотрен способ получения рисунков замкну-

тыми контактными узорообразователями при условии, что число

делений в периметре узорообразователя Р меньше числа игл N

в игольнице машины. Однако существуют такие машины, в ко-

торых роль узорообразователя играет стальная лента большой

длины. В данном случае число делений может быть очень боль-

шим и создаются условия, при которых P>N.

Рассмотрим последовательность расчета рисунков на круг-

лых машинах, когда число делений узорообразующей системы

больше числа игл машины.

Первый способ расчета. При первом способе расчета узор не

будет иметь восхождения. Этот способ применяется при усло-

вии, когда Р делится на N без остатка; в этом случае ширина

раппорта равна числу игл на машине. Узор, полученный на ма-

шине при b = N, не имеет восхождения.

Так как каждый ряд раппорта узора выполняется своим

участком ленты, равным числу игл, то высота раппорта будет

равна числу участков, укладывающихся во всей длине ленты Р,

т. е. высота раппорта, образованная одной системой, всегда

равна числу делений узорообразующей системы, деленному на

число игл, т. е.

Высота раппорта, образованная несколькими системами, будет

где п — число петлеобразующих систем на машине.

Высота раппорта при данном способе расчета будет зависеть

от того, какой длины ленту имеет каждая система и какое число

систем имеется на машине. Число делений ленты в игольных

шагах должно делиться на число N. Поэтому при установлении

длины ленты в метрах определяют величину игольного шага

в миллиметрах, затем находят число игольных шагов в выбран-

ной длине ленты. Делением полученного числа игольных шагов

на число игл устанавливают точно ее необходимую длину для

выполнения проектируемого узора.

Для получения ширины раппорта меньшей, чем число игл

на машине, при первом способе расчета необходимо соблюдать

следующее правило: ширина раппорта должна быть равна

всему числу игл или укладываться целое число раз в числе игл

на машине, т. е.

= или 6 =

где Z — целое число.

Обычно ширина раппорта всегда принимается в несколько

раз меньшей, чем число игл на машине. Раппорты в этом слу-

чае располагаются и по вертикали, и по горизонтали без сме-

щения.

Пример 1. Определить необходимую длину ленты для выполнения рап-

порта узора при /г=20 рядов;

= 25 петель на машине 9 класса с числом

игл 525.

1. Рассчитаем число делений ленты в игольных шагах U, необходимое для

выполнения данного узора:

It = 525-20= 10 500.

2. Найдем величину игольного шага:

К 9

3. Определим длину ленты в метрах Im'-

/«= 10 500 0,00282 = 29,61 ж.

Пример 2. Определить границы раппорта узора для машины 9 класса

с числом игл 525 и числом систем 4. Возможная длина ленты — 30 м.

1. Определим игольный шаг:

25,4

Т =

25,4

= 2,82 мм.

2. Определим число игольных шагов во всей ленте:

3000:2,82 = 10 603.

3. Выберем ширину раннорта из произведешш некоторых сомножителей

525

105

6 = 5-5 = 25.

4. Рассчитаем высоту раппорта при работе с одной системой:

10 603

525

= 20.

Остаток не принимается во внимание, и лента устанавливается с числом

делений, которое делится на величину Р без остатка. В данном случае Р—

400.

5. Найдем общую высоту раппорта узора:

Н = hn = 20-4

v==

80.

6. Определим номера рядов, выполняемых участками ленты в каждой

системе (табл. 10):

Таблица 10

Номера секций

S о

3 4 б

7 8

9 10 и

16 п

9 13 17

61 65

69 73 77

26 30

34 38

42 46 50 54 58

62 66 70

74 78

III

39 43

51 55

59 63

44 48

52 56

Изобразив узор в найденных границах раппорта, запишем чередование

работающих и неработающих делений ленты.

Второй способ расчета. По второму способу расчет узоров

на машинах с узорообразующими механизмами, в которых

P>N, производится при условии, что Р не делится на N без

остатка. Рисунок в этом случае получается с восхождением, но

размеры раппорта могут быть настолько большие, что это вос-

хождение легко будет скрыть различными вариантами узора.

Преимуществом второго способа является то, что в данном

случае значительно сокращается расход ленты.

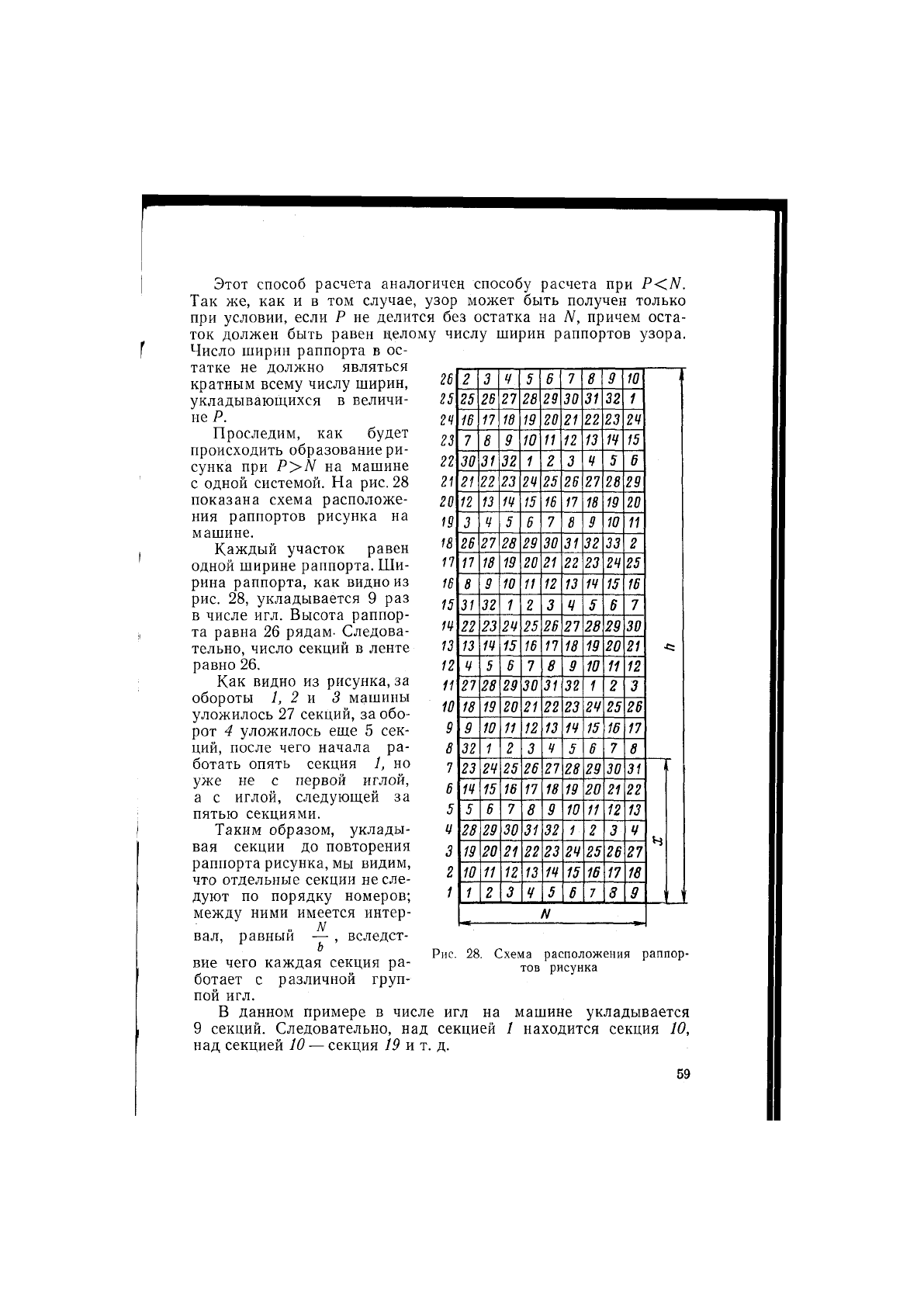
Этот способ расчета аналогичен способу расчета при P<N.

Так же, как и в том случае, узор может быть получен только

при условии, если Р не делится без остатка на N, причем оста-

ток должен быть равен целому числу ширин раппортов узора.

Число ширин раппорта в ос-

татке не должно являться

кратным всему числу ширин,

укладывающихся в величи-

не Р.

Проследим, как будет

происходить образование ри-

сунка при P>N на машине

с одной системой. На рис. 28

показана схема расположе-

ния раппортов рисунка на

машине.

Каждый участок равен

одной ширине раппорта. Ши-

рина раппорта, как видно из

рис. 28, укладывается 9 раз

в числе игл. Высота раппор-

та равна 26 рядам- Следова-

тельно, число секций в ленте

равно 26.

Как видно из рисунка,за

обороты 1,2 м 3 машины

уложилось 27 секций, за обо-

рот 4 уложилось еще 5 сек-

ций, после чего начала ра-

ботать опять секция 1, но

уже не с первой иглой,

а с иглой, следующей за

пятью секциями.

Таким образом, уклады-

вая секции до повторения

раппорта рисунка, мы видим,

что отдельные секции не сле-

дуют по порядку номеров;

между ними имеется интер-

вал, равный — , вследст-

26 2 3

5 6

26 21

30 31 32

23 7

9 10

12 13 14

22 30

31 32

2 3

5 6

21 21 22 23 24

26 27

28 29

го 12

14 15 16 11

19 20

Ч 5

8 9 10

18 26

29 30

32 33 2

9 10 11 12

15 16

32 1

2 3

5 В

24 25 26

15 16 п

12 Ч 5 6

7 8 9

10 11

11 27

28 29 30

1 2 3

18 19 20 21 22

25 26

9 9 10 11 12 13

14 15

16 17

2 3

5 6

23 24

28 29 30

14 15 16 п 18

19 20 21

5 5 6

8 9 10 11

12 13

30 31

32 1

2 3

20 21

22 23

26 27

г 10 11

12 13

1 1

вие чего каждая секция ра-

ботает с различной груп-

пой игл.

В данном примере в числе игл на

9 секций. Следовательно, над секцией

над секцией 10 — секция 19 и т. д.

Рис. 28. Схема расположения

тов рисунка

раппор-

машине укладывается

1 находится секция 10,

На бсновании схеМы образования рйСунка можно написать

уравнение числа Р, при котором может быть получен узор в за-

висимости от числа N и остатка, т. е.

Р = Nz + М — .

Таким образом, для получения узора необходимо, чтобы ши-

)ина раппорта его укладывалась целое число раз в числе игл.

В то же время ширина раппорта должна укладываться целое

число раз во всем периметре узорообразующей системы.

Отсюда можно заключить, что ширина раппорта и есть наи-

больший обший делитель чисел, выражающих число игл на ма-

шине и число делений узорообразующей системы. Высота рап-

порта будет равна числу делений Р, деленному на ширину рап-

порта, т. е.

Чтобы определить, каким номером секции выполняется тот

или иной ряд раппорта узора, надо к номеру секции, работаю-

щей в предыдущем ряду, прибавить число — , в данном слу-

чае равное 9.

Если обозначить буквой ki номер секции, работающей

в ряду /, буквой ^2 —номер секции, работающей в ряду 2,

и т. д., то получим:

где q — номер ряда, для которого определяется номер узорообразующей сек-

ции;

у — число полных оборотов узорообразующей системы до подхода ее к

данному ряду раппорта.

Таким образом, для определения номера секции узорообра-

зующей системы для любого ряда раппорта q нужно к единице

прибавить величину-у . умноженную на число, указывающее

номер искомого ряда раппорта без единицы.

Установив границы раппорта, прежде чем вписывать узор,

надо определить величину восхождения соседнего раппорта по

высоте, чтобы скрыть ее при проектировании узора, т. е. опре-

делить, на сколько рядов поднимается один раппорт по отноше-

нию к другому в направлении петлеобразования.

На рис. 28 видно, что восхождение х=7. Первая секция

всегда располагается в одном ряду с последней секцией и сле-

дует за ней по направлению петлеобразования. В данном при-

мере за секцией 32 следует секция 1.