Малафіїк І.В. Дидактика
Подождите немного. Документ загружается.


381Роздiл 10. Теоретичні засади окремих навчальних технологій
31. Мойсеюк Н.Є. Педагогіка: Навч. пос. – 2е вид. – 1999. – 350 с.
32. Момот Л.Л. Проблемнопошукові методи навчання в школі. – К., 1984.
– 63 с.
33. Морозова Н.Г. Учителю о познавательном интересе. – М., 1979. – 47 с.
34. Новое педагогическое мышление / Под ред.А.В.Петровского. – М.:
Педагогика, 1989. – 280 с.
35. Нісімчук А.С., Падалка О.С., Шпак О.Т. Сучасні педагогічні технології:
Навч. пос. – К.: Видавничий центр “Просвіта”, Пошукововидавниче агент
ство“Книга Пам’яті України”, 2000. – 368 с.
36. Оконь В. Введение в дидактику / Пер. с польск. Л.Г.Кашуркевича, Г.Го
рина. – М., 1990.
37. Онищук В.А. Урок в современной школе. – М., Просвещение – 1991.
– 27 с.
38. Паламарчук В.Ф. Школа учит мыслить. – 2е изд., перераб., доп. – М.,
1980. – 208 с.
39. Педагогический поиск / Сост. Н.Н.Баженова. – М.: Педагогика, 1987.
– 544 с.
40. Педагогічний словник. / Упор.С.У.Гончаренко. – К.: Вища школа, 1999.
– 568 с.
41. Пидкасистый П.И. Учебное пособие для студентов педагогических ву
зов и педагогических колледжей. – М., Педагогическое общество России, 1998.
– 640 с.
42. Пидкасистый П.И. Самостоятельная познавательная деятельность
школьников в обучении. – М., 1980.
43. Подласый И.П. Педагогика: 100 вопросов – 100 ответов: Учеб. пособие
для вузов – М.: ВЛАДОС ПРЕСС, 2001.
44. Подласый И.П. Как подготовить эффективный урок. – К., 1989.
45. Проколиенко Л.Н. Методологические проблемы использования компь
ютера в обучении // Вопр. Психологи, 1986. – С. 4243.
46. Тестова перевірка знань учнів / За ред.Н.М.Розенберга. – К.,
1973. – 168 с.
47. Урок физики в современной школе: Творч. поиск учителей: Кн.для учи
теля / Сост. Э. М. Браверман; Под ред. В. Г. Разумовского. – М.: Просвеще
ние, 1993. – 288 с.
48. Учителіметодисти радять і пропонують: Пос. для вчит. упор.А.Я.Са
мардак; За ред.О.І.Бугайова. – К.: Рад.школа, 1990. – 143 с.
49. Ушинский К.Д.Избранные педагогические произведения. – М.:
Про
свещение, 1967.
50. Шевченко С.Д. Школьный урок: как научить каждого. – М.: Просве
щение, 1991. – 175 с.

382
Додаток 1
Народна дидактика
Будеш трудитися – будеш кормитися.
Без діла слабіє сила.
Без муки нема науки.
Без терпіння нема учіння.
Біда вимучить, але вона й вчить.
Була б охота, а робота знайдеться.
Б’ють – не на лихо учать.
Берись дружно, не буде сутужно.
Без труда нема плода.
Вола в’яжуть мотузками, а людину словами.
Все любить міру.
Всяк розумний посвоєму: один спершу, другий потім.
Вік живи – вік учись.
Всяке діло починай з голови.
Вір своїм очам, а не чужим речам.
Вміння робити на плечах не носити.
Вмить збагнув – вмить забув.
Всякий коваль свого щастя.
Всяка порада тільки до розуму.
Вчитись – що візок пхати вгору.
Вчитись ніколи не пізно.
Гни дерево поки молоде, вчи дитя, поки мале.
Говори мало, слухай багато, а думай ще більше.
Гарно того вчити, хто хоче все знати.
Годину полінувавсь і став ледачим на все життя.
Голова без язика, немов черевик без шнурка.
Голова здорова, а в ній полова.
Горбатого могила справить.
Голова без розуму, як ліхтар без свічки.
Де більше науки, там менше муки.
Доки не впріти, доти не вміти.
Добрий приклад кращий за сто слів.
Дитині треба працювати з того моменту, коли вона навчилась тримати
ложку.
Де гра, там і радість.
Добрі діти доброго слова послухаються, а лихі і дрючка не бояться.
Діти, як квіти: полий, то ростимуть.
Дізнавайся світа, поки служать літа.
Дерево і вчитель пізнаються за плодами.

383Додатки
Добре ім’я краще багатства.
Для навчання старості немає.
З терпіння набираються вміння.
Знання не камінь, за плечима не носити.
З ким поведешся, від того й наберешся.
З розумним будеш розумним, а з дурним і сам будеш таким.
Звичка – друга натура.
Знання робить життя красним.
За науку цілуй батька й матір в руку.
Злість – погана порадниця.
Знаєш і вмієш – навчи іншого.
З першого слова видно – розумний чи дурний.
З самого початку думай, який буде кінець.
Знання дорожче за багатство.
І давня наука дає нові плоди.
Краще раз побачити, чим сто разів почути.
Краще догана розумного, чим похвала дурного.
Коли зореш мілко, посієш рідко, то і вродить дідько.
Краще з розумним згубити, ніж із здурнем найти.
Краще на п’ять хвилин раніше, ніж за годину пізніше.
Краще не народитися, ні не вчитися.
Кінець – діло красить.
Книга вчить, як на світі жить.
Коли дитини не навчити в пелюшках, то не навчиш у подушках.
Лінивий і серед ріки просить напитися.
Ліпше раз переписати, ніж десять раз писати.
Людей питай, а свій розум май.
Ледачий в день до школи плачучи йде.
Легше рано лягати спати, ніж рано вставати.
Маленька праця краща за велике безділля.
Майстер, що за все хапається, втрачає майстерність.
Матимеш терпіння – дочекаєшся, коли море вгамується.
Мудрий той, хто думає, як зробити.
Мудрий дев’ять разів подумає, перш ніж сказати.
Мудрим ніхто не родився, а навчився.
Мудрий не все скаже, що знає.
Найбільша сила – терпіння.
Наука не веде до бука.
Наука – срібло, практика – золото.
Наука не пиво, в рот не ввіллєш.

І. В. Малафіїк. Дидактика384
Не відкладай на завтра те, що можна зробити сьогодні.
Не всяк той вчений, хто читати вміє.
Не знаєш броду – не лізь у воду.
Не замочивши ніг, риби не зловиш.
Не кажи “гоп”, поки не перескочиш.
Не краса красить, а розум.
Не намучишся – не научишся.
Нема науки без муки.
Найкращий контроль – власна совість.
Надто багато знай, та й ще питай.
Не шукай правди в других, коли в тебе її немає.
На дурнів не вчаться.
Наука в ліс не веде, а з лісу виводить.
Науки не носять за плечима.
Навдогад тільки постоли плетуть.
Навчай інших і сам навчишся.
На те і голова, щоб в ній розум був.
Не збирай сину худоби, збери йому розум.
Не всякий, хто читає, в читанні силу має.
Не на користь книжку читав, коли вершки тільки хапав.
Не роби нікому того, що тобі не мило.
Не почавши, не кінчиш.
Не перо пише, а розум.
Не сокира теше, а чоловік.
Не лінуйся рано вставати і з молоду багато знати.
Не все, що написано, чогось варто.
На те коня кують, щоб не спотикався.
Не кажи не вмію, а кажи навчусь.
На довгім віку всього доведеться.
Оце тобі, тату, за твою науку: сядь собі у припічку, колиши онука.
Освічений дикун в сто раз страшніший за неосвіченого.
Око бачить далеко, а розум ще дальше.
Посієш вчасно, то і родить рясно.
Птаха пізнають по пір’ю, а людину по справах.
Посієш вчинок – пожнеш звичку, посієш звичку – пожнеш характер.
Приклад кращий за правило.
Перед тим, як карати, полічи до ста.
Праця – душа всього життя.
Пригоди учать згоди.
Потрібно учитися, завжди пригодиться.
Ранні пташки воду п’ють, а пізні – сльози ллють.
Роби добро і не дивись для кого.
Розум – скарб на тисячу поколінь.

385Додатки
Розумний не соромиться і молодшого питає.
Розум за гроші не купиш.
Розумний батько сина спитати не соромиться.
Розум за морем не купиш, коли його дома нема.
Робиш один раз, а залишиться навіки.
Скільки ти знаєш мов, стільки разів ти людина.
Сьогоднішньої роботи на завтра не відкладай.
Спершу треба розсудити, а тоді робити.
Спитаєш – сором на годину, не спитаєш – можна на все життя.
Спочатку аз та буки, а потім будуть науки.
Світ розуму вчить.
Сила добре, а розум – краще.
Сказаного не повернеш, загубленого не знайдеш.
Скільки голів, стільки й умів.
Сміливість від знань виросте.
Се не на рік, а на цілий вік.
Свій розум май і людей питай.
Сила без голови шаліє, а розум без сили мліє.
Сім раз відмір, а один відріж.
Слово не горобець, вилетить – не спіймаєш.
Слова – полова, а праця – диво.
Треба нахилитися, щоб з криниці води напитися.
Тоді учи, як упоперек на лавці лежить, а як уздовж ляже, тоді вже його труд
но вчити.
Треба розумом надточити, де руки не візьмуть.
Той дає раду, хто знає правду.
Умій сказати, умій і змовчати.
Учитель – це на три світа: теперішній, минулий, майбутній.
Учи сина, як годуєш, бо тоді вже не навчиш, як тебе годуватиме.
У підлітка розум і серце часто не владу.
Учись – на старість буде як знахідка.
Учений іде, а неуч слідом спотикається.
Хто на зроблене озирається, той рідко помиляється.
Хто відкидає мале, той не знайде великого.
Хто нічого не робить, той ніколи не має часу.
Хто рано встає, тому Бог дає.
Хто рано підводиться, за тим і діло водиться.
Хто думає, той і розум має.
Хто знання має, той і мур зламає.
Хто шукає, той знайде.
Хто не раз був битий, той уміє жити.
Хто сам не горить, той інших не запалить.
Хто спішить, той людей смішить.

І. В. Малафіїк. Дидактика386
Хитрощами довго не проживеш.
Хто людей питає, той розум має.
Хто каже правду, той не грішить.
Хто добре учиться, той добре робити буде.
Хто багато зробив, той і багато знає.
Хто хоче знати, тому треба менше спати.
Хто що вміє, тим і діє.
Чого Івась не навчився, того Іван не знатиме.
Чув дзвін, та не знає, де він.
Чим більше науки, тим довші руки.
Чесна праця – наше багатство.
Чого в молодості навчишся, на старість як знайдеш.
Чим дальше в ліс, тим більше дров.
Читати – друзів шукати.
Шануй учителя, як родителя.
Шануй батька й матір.
Що в молодості не здобудеш, то в зрілості не знайдеш.
Що голова, то й розум.
Яке коріння, таке й насіння.
Як часто будеш називати людину свинею, то вона й захрюкає.
Яблуко від яблуні недалеко падає.
Язик до Києва доведе.
Як вовка не годуй, він все одно в ліс дивиться.
Як джерело чисте, то й струмок прозорий.
Як не коваль, то й рук не погань.
Як не наївся, то й не налижешся.
Як розумна голова, то й губи стулені.
Якщо хочеш їсти калачі, не сиди на печі.
Як нема свого ума, то в сусіда не позичиш.
Який палець не вріж, однаково болить.
Якщо розуму немає, то в аптеці не купиш.
[Ці приказки, поговірки, і прислів’я ми взяли
з методичної розробки: Б.Н.Митюров,
І.В.Малафіїк, Б.П.Бричок. Нехай мова
вчителя рясніє народною мудрістю. –
Рівне, 1998. – 54 с.]

387Додатки
Додаток 2
Деякі аспекти обробки результатів педагогічного експерименту
Обробка результатів педагогічного експерименту вимагає застосування
методів теорії ймовірностей та математичної статистики.
Після закінчення експерименту учням експериментальних та контрольних
класів пропонують виконати одну і ту саму контрольну роботу, один і той са
мий текст або одне і те саме контрольне завдання. Нехай результати виконан
ня учнями цих завдань оцінюємо за п’ятибаловою шкалою оцінок. Для по
рівняння навчання в експериментальних і контрольних класах визначають
середній оцінювальний бал. Спосіб його визначення зрозумілий з формули:
,
54321
54321
N
nnnnn
X
++++
=
(2.1.)
де N = n
1
+ n
2
+ n
3
+ n
4
+ n
5
– кількість, які виконували роботу. n
1
… n
5
–
кількість учнів, які отримали оцінки відповідно 1, 2, 3, 4, 5.
Крім середнього балу для оцінки результатів застосовують моду і медіану.
Мода – це оцінка, яка повторюється найбільшу кількість разів, або це оцінка,
яку отримала найбільша кількість учнів. Наприклад, контрольні завдання учні
виконали так, що їх відповіді оцінили таким чином: «1»– 0 учнів, «2»– 3 учні,
«3»– 9 учнів, «4»– 14 учнів, «5»– 5 учнів (усього 31 учень). Очевидно, модою
даного спектра є оцінка 4.
Щоб визначити медіану, потрібно з усіх оцінок (окремо для контрольних і
окремо для експериментальних класів) створити варіативний ряд за спадною
або за зростаючою рисою. Наприклад, за вищенаведеними результатами можна
скласти такий ряд: 2,2,2,3,3,3,3,3,3,3,3,3,4,4,4,4,4,4,4,4,4,4,4,4,4,4,5,5,5,5,5,5.
Медіана – це оцінка, яка розсікає даний варіативний ряд на дві рівні частини.
Це, очевидно, є оцінка, яка стоїть на 16му місці , тобто 4. Для даних результатів
середній бал дорівнює 3, мода – 4, а медіана – 4. Залежно від завдань експери
менту використовують ту чи іншу характеристику результатів навчання.
Оцінки, які отримують учні, прийнято вважати випадковими дискретними
величинами. Учень може отримати одну з п’яти оцінок. На перший погляд може
здатися, що для того, щоб задати дискретну випадкову величину, достатньо пере
рахувати всі її можливі значення. Однак випадкові величини можуть мати одна
кові значення, але різні ймовірності. Для засідання дискретної випадкової вели
чини потрібно не тільки вказати всі можливі її значення, а й потрібно вказати ще
і їх імовірності. Ймовірність – це величина, яка визначається за формулою:
,)(
n
m
AP =
(2.2.)
де m – кількість елементарних випадків, які сприяють певній події, а n –
кількість всіх можливих випадків. Наприклад, нехай у ящику є 6 однакових
куль, причому 3 з них червоні, 2 – білі, 1 – чорна. Очевидно, шансів вийняти з
ящика червону кулю найбільше. Ймовірність події А
1
– витягти червону кулю:
;
2
1
6
3
)(
1
===
n
m
AP
події А
2
– витягти білу кулю:
;
3
1
6
2
)(
2
==AP
події А
3
–
І. В. Малафіїк. Дидактика388
витягти чорну кулю:
.
6
1
)(
3
=AP
Закон розподілу дискретної випадкової ве
личини – це відповідність між можливими значеннями випадкової величини і
їх імовірностями. Він задається таблично, графічно, аналітично. Ось приклад
задання закону розподілу оцінок контрольної роботи:
Х (оцінки): 5 4 3 2 1
Р (імовірність): 0,17 0,5 0,2 0,13 0
Зауважимо, що ймовірність визначається до експерименту, а відносна ча
стина – після експерименту.
Оцінки здебільшого підлягають так званому нормальному розподілу ймо
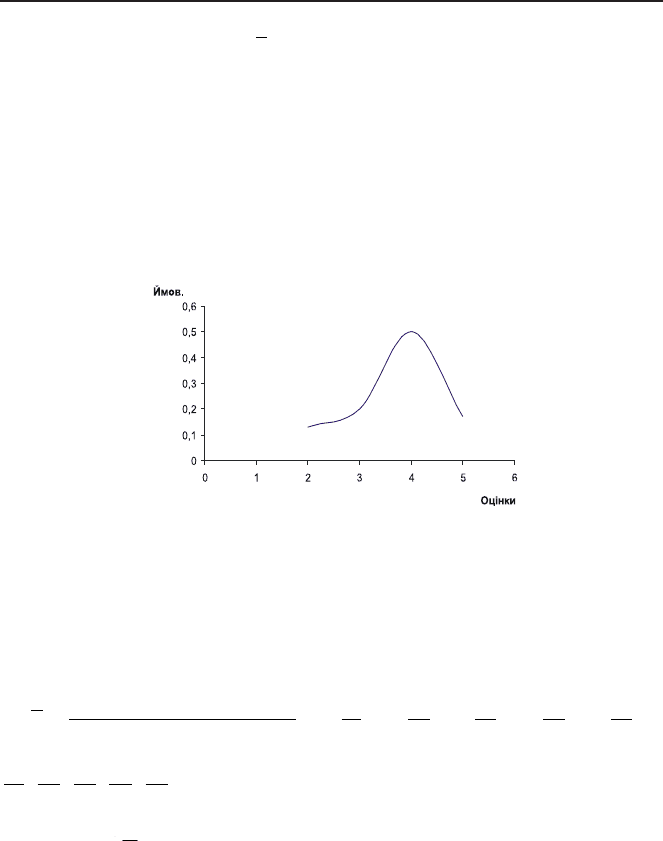
вірностей. Графік функції нормального розподілу ймовірностей називають
нормальною кривою (кривою Гауса). Він має вигляд:
Рис. 2.1.
Закон розподілу ймовірностей повністю характеризує випадкову величи
ну. Однак дуже часто він буває невідомим. Тоді випадкову величину доводить
ся описувати числами, числовими характеристиками. Однією з них є матема
тичне чекання. Математичним чеканням дискретної випадкової величини
називають суму добутків усіх її можливих значень та їх імовірностей.
Формулу для визначення середнього балу можна переписати так:
.54321
54321
5
4
3
21
54321
54321
N
n
N
n
N
n
N
n
N
n
nnnnn
nnnnn
X ⋅+⋅+⋅+⋅+⋅=
++++
++++
=
N
n
N
n
N
n
N
n
N
n
54321
,,,,
– ймовірності оцінок 1, 2, 3, 4, 5; їх позначимо через р з
індексами 1, 2, 3, 4, 5. Отже, маємо:
.54321)(
54321
pppppxMX ⋅+⋅+⋅+⋅+⋅==
Це і є математичним чеканням величини оцінки. (Математичне чекання
приблизно дорівнює середньому значенню випадкової величини). Як бачи
мо, знаючи характеристики результатів експерименту: середній бал, моду, ме
діану, закон розподілу ймовірностей оцінок учнів в експериментальних і кон
трольних класах, математичне чекання, можна порівняти методи чи технології
навчання.

389Додатки
Додаток 3
Типовий навчальний план загальноосвітніх навчальних
закладів ІІ ступеня з українською мовою навчання
(перехідний)
Таблиця 3.1.
Кількість годин на тиждень у класах №
з/п
Навчальні предмети
5 6 7 8 9
Інваріантна складова
1. Українська мова і література 6 5 5 5 4,5
2. Зарубіжна література 2 2 2 2 2
3. Іноземна мова 4 3 3 3 3
4. Математика 4 4,5 4,5 4,5 4,5
5. Історія України 1 – 1 1 2
6. Всесвітня історія – 2 1 1 1
7. Правознавство – – – – 1,5
8. Рідний край (Природознавство)
Довкілля*
1 *
9. Біологія – 2 2 2 1,5
10. Географія – 2 2 2 2
11. Фізика – – 2 2 2,5
12. Хімія – – – 2 2
13. Музика 1 1 1 1 –
14. Образотворче мистецтво 1 1 1 – –
15. Фізична культура і здоров’я 2 2 2 2 2
16. Основи безпеки життєдіяльності 0,5 0,5 0,5 0,5 0,5
17. Трудове навчання, креслення 2 2 2 2 2
РАЗОМ 24,5 27 29 30 31
Варіативна складова
Додатковий час на предмети
інваріантної складової, предмети за
вибором, факультативи, додаткові
індивідуальні та групові заняття
4,5 5 5 6 6
Гранично допустиме навчальне
навантаження на учня (без урахуван-
ня факультативів, додаткових занять):
• 5-денний робочий тиждень
• 6-денний робочий тиждень
26
28
29
31
31
33
32
34
32
35
Усього фінансується покласно (без
урахування поділу класів на групи)
29 32 34 36 37
Примітка: *Інтегрований курс «Довкілля» може вивчатися у 56 класах (у
6му класі за рахунок предметів «Біологія» та «Географія»).
І. В. Малафіїк. Дидактика390
Додаток 4
Типовий навчальний план загальноосвітніх навчальних
закладів ІІІ ступеня з українською мовою навчання
(перехідний)
Таблиця 4.1.
Кількість годин на тиждень у класах
за напрямами навчання
загально-
освітній
гуманітарний
природничо-
математич-
ний
технологічний
№
з/п
Навчальні предмети
10 11 10 11 10 11 10 11
1 2 3 4 5 6 7 8 9 10
1. Українська мова 2 2 2+(1) 2+(1) 2 2 2 2
2. Українська література 2 2 3+(1) 3+(1)
3. Зарубіжна література 2 2
2 2 2 2
4. Іноземна мова 2 2 3 3 2 2 2 2
5. Друга іноземна мова
або мова національної
меншини
(3) (4)
6. Математика 4 4 3 3 4+(3) 4+(3) 3 3
7. Інформатика 1+1* 1+1* 1+(1) 1+(1) 1+1* 1+1* 1 1
8. Історія України 2 1б5 2+(1) 1,5+(1) 1 1 1 1
9. Всесвітня історія 1,5 1,5 1,5 1,5+(1) 1 1 1 1
10. Людина і суспільство/
Основи філософії
(1) 1+(1) 1 1
11. Географія 1 1+(1) 1+(1) (1) 1
12. Основи економіки (1) 1 1 1 1
13. Біологія, основи
екології
1 2 1 1 1+(1) 2+(1,5 1 2
14. Фізика 3 3,5 3+(1) 4+(1,5 3 3,5
15. Астрономія
0,5
2
2
1 0,5
16. Хімія 2 2 1 1 2+(1) 2 2 2
17. Худ. культура/ Основи
етики/ Основи естетики
1+(1) 1+(1)
18. Фізична культура і
здоров’я, ДПЮ, ОБЖ
3 3 3 3 3 3 3 3
19. Трудове навчання/
Технології
2 2 5 5
20. Креслення 1 1
РАЗОМ
2
9,5+(1) 30+(1) 31,5 31 29 30 29 30
