Любушин А.А. Фрактальный анализ временных рядов
Подождите немного. Документ загружается.


11
f) Значение параметра Херста 1 для самоподобного процесса. Действительно, имеем:
H ≤
|(2)| |(2) (1) (1)| |(2) (1)| |(1)|2 |(1)|
MZ MZ Z Z MZ Z MZ MZ=−+≤−+= (37)
С другой стороны, в силу самоподобия |(2)|2 |(1)| 2 2 1
HH
MZ MZ H
=
⇒≤⇒≤ .
g) Если , то
1H =
2
() () (,)
H
M
ZsZt st st
σ
=Γ = . Отсюда
22 22 22 2
(() (1)) ()2 (()(1)) (1) ( 2 ) 0MZt tZ MZ t tMZtZ tMZ t tt t
σ
−= − + =−+= (38)
то есть () (1)
Z
ttZ= почти всюду.
Пусть ()
Z
t Hsssi∈ , и ()01H<<
Z
t - гауссовский процесс. Тогда ()
Z
t называется
фрактальным броуновским движением и обозначается ()
H
B
t . Если , то 0.5H =
()
Z
t
является обычным броуновским движением или винеровским процессом. Нетрудно
получить, что в случае, если
2
0.5
(,) min(| |,| |)st s t
σ
Γ=
() ()sign t sign s
=
и , если
. Одно из возможных представление fBm:
0.5
(,) 0stΓ=
() ()sign t sign s≠
0.5 0.5
0.5
() [( ) ( ) ] ( ); max(0, )
HH
HH
B
tk tu u dBuu u
+∞
−−
++ +
−∞
=−−− =
∫
(39)
Здесь
H
k - нормировочная постоянная. Если выбрать:
2
1
0
2(1.5)
,
(0.5)(22)
() , 0,(0.5) ,(1)1,(1)
H
tu
HH
k
HH
uetdtu n n
π
∞
−−
⋅Γ −
=
Γ+ ⋅Γ−
Γ= > Γ = Γ= Γ+=
∫
!
=
(40)
то . Хаусдорфова размерность реализаций
22
() 1
H
MB t
σ
= ()
H
B
t равна 2.
H
DH=−
Рассмотрим приращения процесса ()
H
B
t : ( 1) ( )
kH H
X
Bk Bk
=
+− . Эта случайная
последовательность называется
фрактальным гауссовским шумом. Для фрактального шума
справедливы утверждения:
(i)
k
X
стационарна.
(ii)
22
0,
kk
MX MX
σ
==
(iii)
22 2 2
() (| 1| 2| | | 1| )/2
HH H
XX i i k
kMXX k k k
γσ
+
==+−+−

12
(iv) Пусть .
0k ≠
Тогда:
0.5 ( ) 0;
00.5 ()
0.5 1 ( ) 0
XX
XX
XX
Hk
Hk
Hk
0;
γ
γ
γ
=⇒
<< ⇒ <
<<⇒ >
=
(v) Пусть . Тогда 0.5H ≠
222
() (2 1)| | , | |
H
XX
kHHk k
γσ
−
−
⋅→∼ ∞
(vi) Пусть
1
() ()
2
ik
XX XX
k
Ske
ω
ωγ
π
+∞
−
=−∞
=
∑
- спектральная плотность стационарной случайной
последовательности
k
X
; ( ) ( )
ik
XX XX
kSed
π
ω
π
γ
ω
+
−
=
∫
ω
. Тогда , т.е. если
(2 1)
() , 0
H
XX
S
ωω ω
−−
→∼
0.5 1 ( ) , 0
XX
HS
ω
ω
<<⇒ →∞→ и сигнал
k
X
носит низкочастотный характер.
Соответственно, спектральная оценка конечной выборки из фрактального броуновского
движения будет иметь поведение:
(2 1)
() , 0
HH
H
BB
S
ωω ω
−+
→∼
5.
Оценка постоянной Херста по экспериментальным данным. Наиболее очевидная
оценка непосредственно из определения показателя, данного самим автором. Пусть
( ), 1,...,
=
x
tt N – анализируемый временной ряд;
<
L
N
– длина скользящего временного
окна;
τ
- номер отсчета правого конца скользящего окна, то есть мы рассматриваем
моменты времени , которые удовлетворяют условию
t 1
−
+≤≤Lt
τ
τ
. Пусть - длина
внутреннего временного окна, которое используется внутри текущего основного окна для
операций усреднения. Мы рассматриваем длины внутренних окон, удовлетворяющие
условию: . Пусть
s
/5≤sL
()
,
1
1
(
=
1)
=
+−
∑
s
su
t
xxut
s
τ
(41)
− выборочная оценка среднего значения на интервале длиной отсчетов, который лежит
внутри текущего основного окна и начинается в точке . Следующий шаг состоит в
вычислении отклонений от среднего значения (41), их накопленной суммы и размаха
накопленной суммы:
s
u
() () () () () () ()
,,,,,,
1
() () , () (), max () min ()
=
Δ=− =Δ = −
∑
t
su su su su su su su
t
t
v
,
x
txtx t xvR t t
ττττττ
ξξ
τ
ξ
(42)

13
для [, 1], [ 1, 1]
∈+− ∈−+−+tuus u L s
τ
τ
. Далее оцениваются дисперсия и среднее значение
отношения размаха к стандартному отклонению:
()
1
,
() 2 () 2 ()
,,
()
11
,
11
() ( ()), ()
(1)
−+
==
=Δ =
−+
∑∑
ss
−+
s
u
su su
tu
L
s
u
R
xt RSs
sLs
τ
τ
τττ
τ
τ
σ
σ
(43)
Показатель Херста ()
H
τ
в текущем временном окне оценивается как наклон кривой
прямой линейной регрессии между значениями
()
ln( ( ))
R
Ss
τ
и . Оценка может получена
как в скользящем временном окне, так и по всей выборке. Заметим, что если ставится задача
оценки постоянной Херста для процесса
ln( )s
()
Z
t Hsssi
∈
, то все вышеизложенные операции
следует производить после перехода к его приращениям, то есть для
() ( 1) ()
=+−
x
tZt Zt.
Другие оценки могут быть основаны на свойстве роста спектра мощности по степенному
закону: при уменьшении частоты. Если использовать не обычные
спектральные оценки, а разложения по системе ортогональных нормированных компактных
базисных функций – вейвлетам [1], то для процесса
(2 1)
() , 0
−+
→∼
H
ZZ
S
ωω ω
()
Z
t Hsssi
∈
оценку постоянной Херста
можно найти по скорости роста средних значений квадратов модулей вейвлет-
коэффициентов:
()
()2 ()
1
||/
=
=
∑
N
j
j
WcN
α
α
α
α
(44)
Здесь
()
j
c
α
- коэффициенты ортогонального дискретного вейвлет-разложения выборки
самоподобного временного ряда,
1,...,
= m
α
- номер уровня детальности разложения,
()
N
α
-
число вейвлет-коэффициентов на уровне детальности
α
,
() ( )
2
−
≤
m
N
α
α
. Тогда, аналогично
соотношению для скорости роста спектра мощности,
21
()
+
∼
H
Ws
αα
, где s
α
- характерный
временной масштаб уровня детальности
α
. Поскольку
(1)
22
+
=÷s
αα
α
, то отсюда следует, что
21
2
log ( )
+
∼
H
W
α
α
(45)
Таким образом, значение коэффициента наклона прямой, подогнанной методом
наименьших квадратов к парам значений
2
(log ( ), )W
α
α
, дает оценку для величины 21
+
H .
6.
Оценка спектра сингулярности по экспериментальным данным. В настоящее время
существуют 2 подхода для оценки спектров сингулярности временного ряда. Первый метод

14
появился раньше и основан на анализе цепей точек максимума модулей непрерывных
вейвлет-преобразований с вейвлетами, обычно равными производной той или иной степени
от функции плотности распределения Гаусса [1]. Второй подход более близок к технике
Херста и основан на анализе зависимости стандартного отклонения или размаха выборки от
ее длины. В последнее время был разработан и активно применяется в различных
приложениях метод анализа флуктуаций после исключения масштабно-зависимых трендов –
Detrended Fluctuation Analysis (DFA) [4]. Сравнительный опыт применения методов
показывает, что метод DFA является более надежным и устойчивым. В то же время для
специального вида самоподобных сигналов, которые могут содержать плато постоянных
значений (типа известной «чертовой лестницы», конструируемой на базе канторовского
множества), метод DFA неприменим и оценка, основанная на непрерывных вейвлет-
преобразованиях, имеет преимущества. Ниже будет использован только DFA и приведены
основные конструкции метода.
Пусть ()
x
t – случайный процесс. Определим в качестве меры (, )
X
t
μ
δ
изменчивости
сигнала ()
x
t на интервале [, ]tt
δ
+ модуль его приращения: ( , ) | ( ) ( )|=+−
x
txt xt
μ
δδ
и
вычислим среднее значение модуля таких мер в степени
q :
(,) {( (,))}
=
q
x
MqM t
δμδ
(46)
Случайный процесс называется масштабно-инвариантным, если при
()
(,) | |
q
Mq
ρ
δδ
∼
0
δ
→
, то есть существует предел:
0
ln ( , )
() lim
ln | |
M
q
q
δ
δ
ρ
δ
→
= (47)
Заметим, что в определении (46-47) величина меры (, )
x
t
μ
δ
может быть взята также как
размах, что ближе к традиционным конструкциям Херста:
(, ) max ( ) min ( )
≤≤+
≤≤+
=
−
x
tut
tut
txu
δ
δ
xu
μ
δ
(48)
Если зависимость
()q
ρ
является линейной:
()qHq
ρ
=
, где , то
процесс называется монофрактальным. В частности, для классического броуновского
движения . Возведение в степень подчеркивает различные типы поведения
,0 1H const H=<<
0.5H =
q
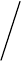
15
сигнала: если 0, то в значение меры (46) основной вклад вносят интервалы времени с
большими отклонениями от тренда, а если 0
>q
<
q , то интервалы времени с малыми
вариациями.
Для вычисления функции ()
q
ρ
по конечной выборке из временного ряда ( ), 1,...,
=
x
tt N
можно применить метод DFA. Пусть - число отсчетов, ассоциированное с варьируемым
масштабом
s
s
δ
:
s
st
δ
=Δ. Разобьем выборку на непересекающиеся малые интервалы длиной
отсчетов:
s
()
{ :1 ( 1) , 1,...,[ / ]}
s
k
I
tkstksk Ns=+−≤≤ = (49)
и пусть
()
( ) (( 1) ), 1,...,=−+ =
s
k
y
txk stt s (50)
участок временного ряда ()
x
t , соответствующий интервалу
()
s
k
I
. Пусть - полином
порядка , подогнанный методом наименьших квадратов к сигналу
(, )
()
sm
k
pt
m
()
()
s
k
y
t . Рассмотрим
отклонения от локального тренда:
(, ) () (, )
( ) ( ) ( ), 1,...,
sm s sm
kkk
ytytpttΔ=− =s (51)
и вычислим значение:
1/
[/]
() (,) (,)
1
1
1
(,) (max () min ()) [ /]
q
Ns
msmsmq
kk
ts
ts
k
Zqs y t y t Ns
≤≤
≤≤
=
⎛⎞
=Δ−Δ
⎜⎟
⎝⎠
∑
(52)
которое будем рассматривать как оценку для . Процедура устранения тренда на
каждом малом участке длиной отсчетов необходима в случае наличия в сигнале трендов
внешнего происхождения. Определим теперь функцию как коэффициент линейной
регрессии между значениями
1/
((,))
q
s
Mq
δ
s
()hq
()
ln( ( , ))
m
Z
qs и : ln( )s
() ()
(,)
mhq
Z
qs s∼ . Очевидно, что
() ()qqhq
ρ
= , а для монофрактального процесса ()h q H const
=
= .
Следующим шагом в мультифрактальном анализе после определения функции
()q
ρ
является вычисление спектра сингулярности
()F
α
, который является с фрактальной
размерности множества точек, в окрестности которых показатель Гельдера-Липшица для
случайных реализаций процесса
()
x
t равен
α
, то есть таких точек , для которых t
16
|( ) ()|| |, 0
+− →∼xt xt
α
δδδ
. Стандартный подход состоит в вычислении статистической
суммы Гиббса:
[/]
(, ) (, )
1
1
1
(,) (max () min ())
Ns
s
msm
kk
ts
ts
k
Wqs y t y t
≤≤
≤≤
=
=Δ−Δ
∑
q
(53)
и определения показателя массы ()
q
τ
из условия , после чего спектр
()
(,)
q
Wqs s
τ
∼ ()F
α
вычисляется согласно формуле:
() max{min( ()),0}
q
Fqq
α
ατ
=− (54)
Сравнивая (52) и (53), нетрудно заметить, что () () 1 () 1
qqqhq
τ
ρ
=
−= −. Таким образом,
( ) max { min( ( ( )) 1, 0}
q
Fqhq
α
α
=−+.
Для монофрактального процесса, когда
()h q H const
=
= , получаем, что ()1FH
=
и
() 0FH
α
α
=∀≠. В частности, положение и ширина носителя спектра ()F
α
, то есть
значения
min max max min
,,
α
αααα
Δ= − и
*
α
- то значение, которое доставляет функции ()F
α
максимум:
*
()max()F
α
F
α
α
=
, являются характеристиками шума. Величину
*
α
можно
назвать обобщенным показателем Херста. Для монофрактального сигнала теоретически
значение
α
Δ должно быть равно нулю, а
*
H
α
=
, но на практике, вследствие конечности
выборки, такие условия не выполняются. Что же касается значения
*
()F
α
, то оно равно
фрактальной размерности точек, для окрестности которых выполняется масштабирующее
соотношение .
()
(,) | |
q
Mq
ρ
δδ
∼
Если оценивать спектр ()
F
α
в скользящем временном окне, то его эволюция может дать
информацию об изменении структуры хаотических пульсаций ряда. Обычно
*
()1F
α
=
, но
встречаются окна, для которых
*
()1F
α
<
. Напомним, что в общем случае (не только для
анализа временных рядов) величина
*
()F
α
равна фрактальной размерности носителя
мультифрактальной меры.
7.
Пример анализа данных. На рис.1(а) представлен график временного ряда наблюдений
за вариациями электротеллурических потенциалов на Камчатке из работы. Общая
продолжительность наблюдений составляет 4 года 8 месяцев (с 01.10.1996 по 23.06.2001),
17
интервал взятия отсчетов 1 час, общее число отсчетов N=41447. Рис.1(б) представляет
приращения временного ряда на рис.1(а).
Рис.1. Графики исходного ряда наблюдений и его приращений.
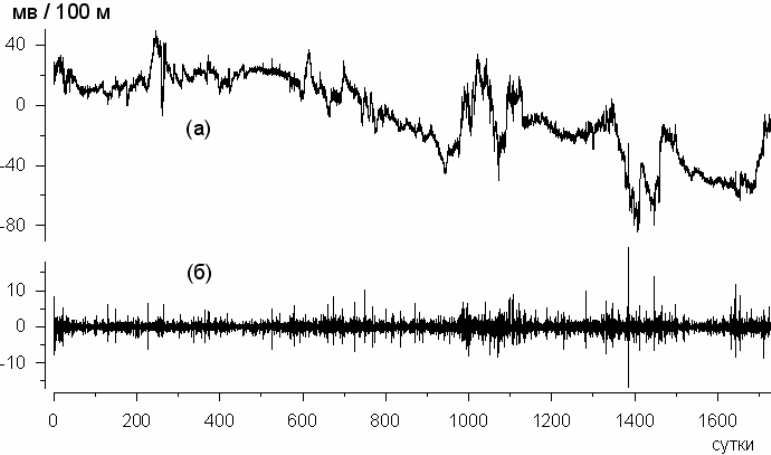
Рис.2 иллюстрирует три различных метода оценки постоянной Херста для временного
ряда, представленного на рис.1. На рис.2(а) оценка получена как коэффициент наклона
прямой наилучшего приближения (штриховая линия) к графику логарифма оценки спектра
мощности в зависимости от логарифма периода. Оценка спектра мощности получена
методом максимальной энтропии Бурга, как результат усреднения спектральных оценок в
скользящем временном окне длиной 2048 отсчетов с использованием модели авторегрессии
200-го порядка внутри каждого окна. На графике рис.2(а) видны спектральные пики,
соответствующие 8, 12 и 24-часовым периодическим компонентам. На рис.2(б) использована
оценка (44)-(45), ортогональный вейвлет выбран из условия минимума энтропии
распределения квадратов вейвлет-коэффициентов [1] и им оказался вейвлет Добеши 18-го
порядка (обнуляющий 9 первых моментов). Наконец, рис.2(б) иллюстрирует применение
статистики (43).
18
Рис.2. Оценка показателя Херста тремя различными методами.
Эти методы дали значения постоянной Херста 0.37, 0.40 и 0.46. Различие в оценках не
очень существенно, но не пренебрежимо мало. Оценка на рис.2(а) представляется наименее
надежной из-за влияния монохроматических пиков. Кроме того, следует учесть, что сигнал,
возможно, является мультифракталом – в этом случае отличия возникают просто вследствие
различия методов и различий в «реакции» на них данных, имеющих на самом деле иную
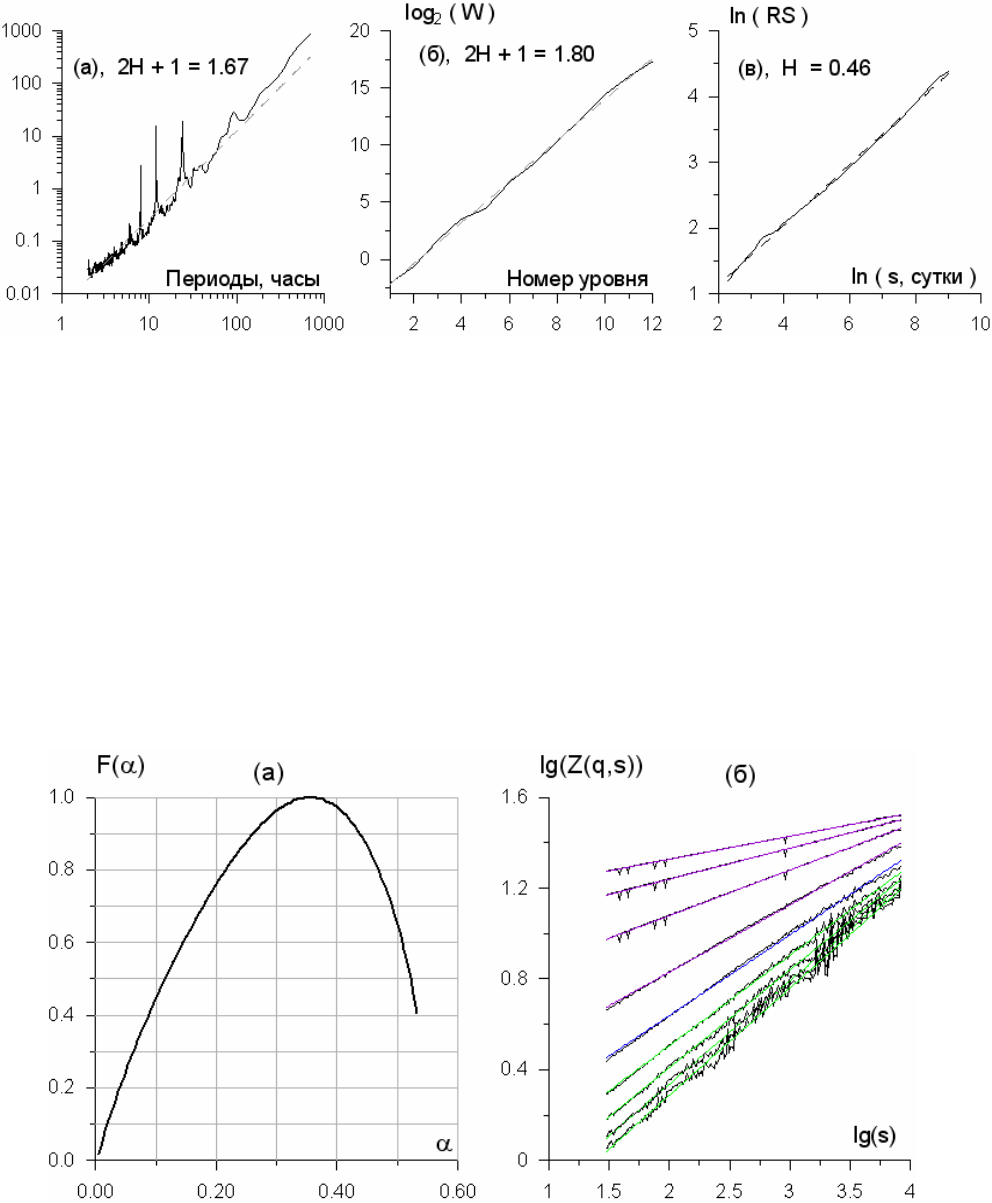
природу. Для выяснения этого вопроса оценим спектр сингулярности для приращений
временного ряда (рис.1(б)) – см. рис.3.
Рис.3. Оценка показателя спектра сингулярности (а) и зависимостей
() ()
(,)
mhq
Z
qs s∼ для
различных показателей степени
q (б)
На рис.3(б) представлены графики как самих величин
()
lg( ( , ))
m
Z
qs , так и линейных
трендов, подогнанных к ним для 9 различных значений степени . Наклон графиков
q
19
линейных трендов есть ничто иное, как функция (), по значениям которой вычисляется
показатель массы
hq
() () 1
=qqhq−
τ
, а далее, согласно формуле (54), и сам спектр
сингулярности. Рис.3(б) демонстрирует хорошее соответствие линейному закону
зависимости
()
lg( ( , ))
m
Z
qs от , то есть, самоподобность сигнала. На рис.3(б) приведены
графики зависимостей с подогнанными линейными трендами для последовательных
значений степени (сверху вниз): 10, 7.5, 5, 2.5, -0.05, -2.5, -5, -7.5 и -10. Масштаб
изменялся начиная с минимального значения 30 отсчетов (30 часов) – чтобы усреднить
периодические компоненты, максимальный период которых равен 24 часам. Следовательно,
как это видно из рис.3(б), сигнал действительно является мультифракталом.
lg( )s
q
s
Для получения временных рядов эволюции значений
*
α
было выбрано скользящее окно
длиной 672 часовых отсчетов, то есть 28 суток, взаимное смещение соседних окон равнялось
24 отсчетам или 1 суткам. Масштабно-зависимые тренды не устранялись, так как
рассматривался ряд в приращениях. Функция () в зависимости
hq
() ()
(,)
mhq
Z
qs s∼
оценивалась в каждом окне для масштабов , изменяющихся от минимального значения 30
отсчетов до максимального, равного одной пятой длины окна. При длине 672 отсчетов,
таким образом, максимальный масштаб равен 137 часов. Кроме того, для этих же временных
окон были получены оценки на основе использования статистик (43) для ряда в приращениях
и (44)-(45) и для исходного ряда. При этом, при построении оценки на основе ортогональных
вейвлет-разложений производилось предварительное устранение тренда внутри каждого
окна полиномом 4-го порядка. Эта предварительная операция удаляла статистически
незначимые низкочастотные вариации и, что более важно, уменьшало искажения значений
вейвлет-коэффициентов на концах выборки вследствие ее конечности. В каждом окне
искался свой ортогональный вейвлет из условия минимума энтропии распределения
квадратов вейвлет-коэффициентов.
s
Из рис.4(а) и (б) видно, что оба метода, (43) и (44)-(45) дают, фактически одно и то же, за
исключением взаимного смещения, которое может быть вызвано несоответствием данных
монофрактальному поведению.
Что же касается прочих графиков на рис.4, то они могут быть использованы при
мониторинге объектов для выделения аномальных признаков. Первым признаком
аномального поведения может служить «провал» вниз значения
*
()F
α
- это может
свидетельствовать о появлении во временном ряду составляющей, поведение которой
достаточно сильно отличается от поведения случайной самоподобной кривой. Кроме того,
вариации наиболее типичного показателя Гельдера-Липшица
*
α
и ширины носителя
Δ
α
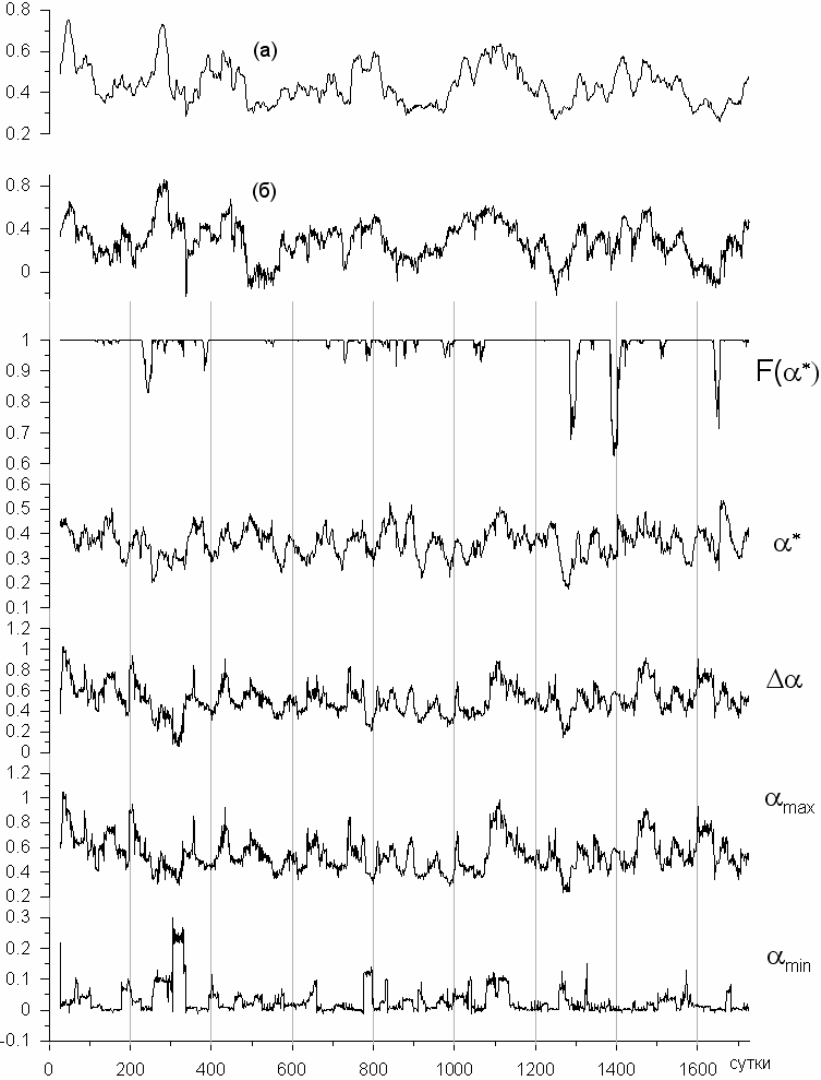
20
спектра сингулярности могут также нести информацию об изменении свойств ряда, которые
скрыты от их выделения более простыми средствами анализа типа линейной фильтрации.
Рис.4. (а) – оценки вариаций постоянных Херста в скользящем временном окне длиной 672
часа RS-методом (формула (43)); (б) – оценка с использованием ортогональных вейвлет
разложений содержимого каждого из окон (формулы (44) и (45)). Прочие графики
представляют изменения параметров спектра сингулярности (обозначения – в тексте).
