Lyons W.C. (ed.). Standard handbook of petroleum and natural gas engineering.2001- Volume 1
Подождите немного. Документ загружается.

Thermodynamics
2
15
For the generalized control volume shown in Figure
2-33,
and entropy balance can be
stated as follows:
Rate of entropy Rate of entropy Rate of entropy Rate of entropy
(
in
)-(
out
)
+
(
production
)
=
(
accumulation
(2-1
14)
In Equation 2-114,
P,
is the rate of entropy production within the control volume;
symbols with dots refer to the time rate of change of the quantity in question. The
second law requires that the rate of entropy production be positive.
P,
2
0
(2-1
15)
Heat Capacity
The heat capacity of a substance is extremely important in thermodynamic analysis
Heat capacity per unit mass is defined by the relationship
involving both the first and second laws.
C=--
SQ
dT
(2-116)
Figure
2-33.
Generalized control volume for a flow system.

2
16
General Engineering and Science
where
SQ
is the heat absorbed by unit mass of the system over the infinitesimal
temperature change, dT.
For
constant
pressure
when only P-V work is involved, the first law yields
CP
=
(S)
For
constant volume
cv
=
(S)
C, is related to Cv by the following expression:
CP
-
cv
=
[
P
+
(3](
g)p
(2-117)
(2-1%)
(2-119)
For an ideal gas for which PV
=
RT/Mw,
with
Mw
representing the molecular
weight, the enthalpy and internal energy are functions only of temperature and
Equation
2-1
19
becomes
c,-cv=P(g)
=-
R
P
M,
(2-1 20)
The ratio of the heat capacity at constant pressure to that at constant volume is
Again, for an ideal gas, this ratio becomes
R
lc=l+-
C”M,
(2-121)
(2-1 22)
Application
of
the Second Law
Heat Engines
The purpose of a heat engine is to remove heat
Q,
from a thermal reservoir at a
higher absolute temperature T,; extract useful work
W;
and reject heat
Q,
to a second
thermal reservoir at a lower absolute temperature
T,.
The device used to obtain the
useful work is the heat engine.
Considering an “ideal” heat engine as the system, the first law as applied to the
engine undergoing a series of reversible changes in a cyclical fashion becomes
CAUl
=
0,
or
W
=
Q,
-
Q,
(2-123)

Thermodynamics
217
The second law yields
(2-124)
To obtain the fraction
of
the heat input
Q,
that is converted to useful work, Equa-
tions
2-123
and
2-124
are combined to give
W
Ti-T,
Qi
Ti
_-
--
(2-125)
This important result is called the
Curnot engine efficiency
and yields the
maximum
thermal efficiency
that can be achieved by
any
heat engine cycle operating between any
two given temperature limits. Heat engines have been proposed
to
operate within
the temperature gradients of the ocean
as
a means of harnessing the vast amounts of
renewable energy available from that source.
Heat
Pumps
A heat pump, which is the opposite of a heat engine, uses work energy
to
transfer
heat from a cold reservoir
to
a “hot” reservoir.
In
households, the cold reservoir is
often the surrounding air
or
the ground while the hot reservoir is the home. For an
ideal heat pump system with
Q1
and
TI
referring to the hot reservoir and
Qr
and T2
referring to the cold reservoir, the work required
is,
from the first and second laws,
(2-126)
Application
of
this result shows that if
100
units of heat
Q,
are needed to maintain a
household at
24°C (297°K)
by “pumping” heat from the outside surroundings at
0°C
(273”K),
it would require a minimum of
(24
x
100/297)
=
8.08
units of work energy.
Refrigeration Machines
Refrigerating machines absorb heat
Q
from a cold reservoir at temperature
T,,
and discharge heat
Q,,
into a “hot” reservoir at Ti.
To
accomplish this, work energy
must also be absorbed. The minimum required work is obtained as shown before,
using the first and second laws:
W
-
Ti -T,
Q,
Ti
(2-127)
Reversible
Work
of Expansion or Compression
Many systems involve only work of expansion
or
compression
of
the system
boundaries. For such systems the first law is written for unit mass
of
fluid as the basis:
dU
=
SQ
-
PdV
(2-128)
where
s,”’
P
dV represents the reversible work
of
compression or expansion.

218
General Engineering and Science
From the second law, for a reversible process,
SQ
dS
=
-
or
SQ
=
TdS
T
(2- 129)
(2-130)
Combining Equations
2-128
and
2-129
gives
dU
=
TdS
-
PdV (reversible, P-V work only)
Reversible Isobaric Processes
The second law is written as
SQ
=
TdS
but, since the heat capacity
C
=
SQ/dT, the second law becomes
CdT
=
TdS
(2-13
1)
Thus, for constant pressure processes, the entropy increase is written as
(2-132)
dT
T
dS
=
C,
-
=
C,d(enT) (reversible isobaric process)
Reversible Constant Volume Processes
A
constant-volume process is called
zsochoric
and, for such processes, the entropy
increase is written as
(2-133)
dT
T
dS
=
C,
-
=
C,d(tn
T)
(reversible isochoric process)
Reversible Isothermal Changes: Maximum Work
The variation
of
entropy with volume and pressure under conditions of constant
temperature
is
determined by using Equation
2-130:
or rearranging:
The variation
of
entropy with pressure is likewise written as
(2-134)
(2-135)
(2-136)

Thermodynamics
219
(2-137)
Combining the first law Equation 2-102 with the second law equation 2-1 11 yields
the expression
dU
=
TdS
-
6W
=
d(TS)
-
6W
or
6W
=
-d(U
-
TS)
which, upon integration between states
1
and 2, yields
W
=
-A(U
-
TS)
(reversible isothermal processes)
(2-1
38)
The combination
of
properties
U
-
TS occurs
so
frequently in thermodynamic
analysis that
it
is
given
a
special name and symbol, namely
A,
the
workfunction
or
maximum
work
(because it represents the maximum work per unit mass, obtainable
during
any
isothermal reversible change in any given system). Therefore, it
is
seen that
W,,,.$,
=
-AA
(reversible isothermal process)
(2-139)
Note that the maximum work depends only upon the initial and final states
of
a
system and not upon the path.
Maximum
Useful Work: Free Energy
The first and second law expressions can be combined and written
for
constant
temperature, constant pressure processes:
dU
=
TdS
-
6W
=
TdS
-
PdV
-
6W'
(2-140)
where
FW'
represents all work energy exchanged with the surroundings except
P-V
work that is written as
PdV.
Therefore, solving for
FW
gives
-6W'
=
dU
+
PdV
-
TdS
(2-141)
or, because both
?'
and
P
are constant,
-6W'
=
dU
+
d(
PV)
-
d(TS)
or
-6W'
=
-d(U
+
PV
-
TS)
By
integration this becomes
W'
=
-A(U
+
PV
-
TS)
=
-A(H
-
TS)
(constant temperature
and
pressure)
(2-142)
(2-143)

220
General Engineering and Science
This expression shows that the maximum possible
useful
work
(Le., reversible work)
that can be obtained from any process occurring at constant temperature and pressure
is a function
of
the initial and final states only and is independent of the path. The
combination of properties U
+
PV
-
TS or
H
-
TS occurs
so
frequently in thermodynamic
analysis that
it
is given a special name and symbol,
F,
thefree
energy
(sometimes called the
Gibbs Free Energy). Using this definition, Equation
2-143
is written
W',,,
=
-AF
(2-144)
Because
F
is a function of temperature and pressure, its differential can be written as
dF
=
(
$)TdP
+
[E)
P
dT
Since
F
=
U
+
PV
-
TS, we can also write
dF
=
dU
+
PdV
+
VdP
-
TdS
-
SdT
Using Equation
2-130,
this becomes
dF
=
VdP
-
SdT
Comparison with Equation
2-145
shows that
($IT
=
(
=
-s
(2-145)
(2-146)
(2-1 47)
(2-148)
(2-149)
Example
2-24
An inventor claims to have devised a CO, compressor that requires no shaft
work. The device operates at steady state by transferring heat from
a
feed stream
of
2
1bJs of
CO,
at
150
psia and
100°F.
The
CO,
is compressed to
a
final pressure of
500
psia and a temperature of
40°F.
Kinetic and potential energy effects are negligible.
A cold source at
-140°F
"drives" the device at a heat transfer rate of
60
Btu/sec.
Check the validity
of
the inventor's claim.
Solution
The device will be impossible
if
it
violates either the first or second law of
thermodynamics. From Figure
2-34
the inlet and outlet properties are:
State
1
State
2
P,
=
500
psia
T,
=
100°F
h,
=
315
BtU/lbm
S,
=
1.31
8
Btu/lb,"R
T,
=
40°F
h,
=
285
BtU/lbm
S,
=
1.21
5
Btu/lb,"R
P,
=
150
psia
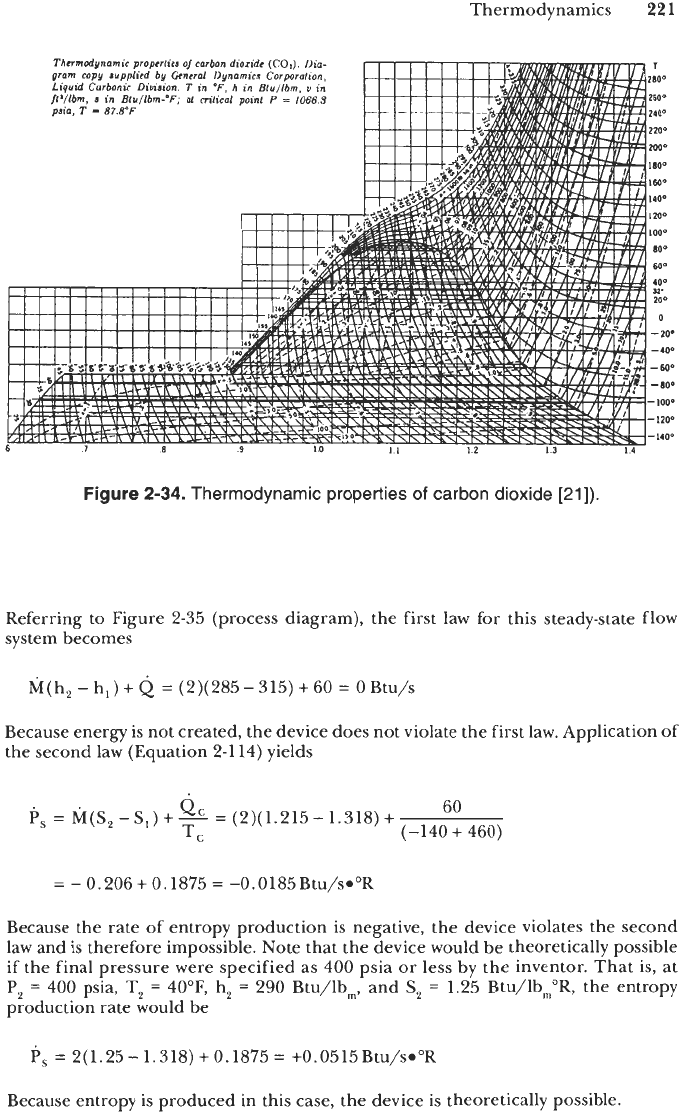
Thermodynamics
221
Figure
2-34.
Thermodynamic properties
of
carbon dioxide
[21]).
Referring to Figure 2-35 (process diagram), the first law for this steady-state flow
system becomes
M(h,-h,)+Q
=
(2)(285-315)+60=OBtu/s
Because energy is not created, the device does not violate the first law. Application of
the second law (Equation 2-1 14) yields
60
P,
=
M(S,-S,)+&
=
(2)(1.215-1.318)+
Tc (-140
+
460)
=
-0.206+0.1875= -0.0185Bt~/s*"R
Because the rate of entropy production is negative, the device violates the second
law and is therefore impossible. Note that the device would be theoretically possible
if the final pressure were specified as 400 psia or less by the inventor. That is, at
P,
=
400 psia, T,
=
40°F, h,
=
290 Btu/lb,, and
S,
=
1.25 Btu/lbm"R, the entropy
production rate would be
Ps
=
2(1.25-1.318)+0.1875
=
+0.0515Btu/s*OR
Because entropy is produced in this case, the device is theoretically possible.

222
General Engineering and Science
1
Cold
I
Qc
=
60
BTWsec
I
I
1
Process Diagram
7
S
Graphical
(b)
T,=
IOOOF
Figure
2-35.
(a) Process diagram.
(b)
Graphical representation
of
Processes
1
and
2.

Thermodynamics
223
Summary of Thermodynamic Equations
The thermodynamic relations formulated earlier for a pure substance are summarized
in Table
2-19
with unit mass
of
fluid
as
the basis. Several additional important relationships
can be derived from them and these are shown in the third column of Table
2-19.
By mathematical manipulation, numerous additional relationships can
be
derived from those given in Table
2-19.
Of
particular significance are expressions
that relate enthalpy
H
and internal energy
U
to
the measurable variables, P,
V,
and T. Thus, choosing the basis as one pound mass,
and
(s)T
=
-P+.(%)
V
(2-150)
(2-151)
Equations
2-150
and
2-151
apply to any substance
or
system and are called
equations
of
state
because they completely determine the state of a system in terms
of
its
thermodynamic properties.
Thermal Properties for Selected Systems
For practical applications of the numerous thermodynamic relationships, it
is
necessary to have available the properties of the system. In general, a given property
of a pure substance can be expressed in terms of any other two properties to completely
define the state
of
the substance.
Thus
one can represent an equation
of
state by the
functional relationship:
P
=
f(T,
V)
(2-152)
which indicates that the pressure is a function
of
the temperature and specific volume.
Plots
of
the properties
of
various substances as well as tables and charts are extremely
useful in solving engineering thermodynamic problems. Two-dimensional represen-
tations of processes on P-V, T-S, or
H-S
diagrams are especially useful in analyzing
cyclical processes. The use of the P-V diagram was illustrated earlier.
A
typical
T-S
diagram for a Kankine vapor power cycle is depicted in Figure
2-36.
For the Rankine cycle, the area enclosed by the line segments connecting points
1,
2,
3,
4,
1
on Figure
2-36
represents the net heat transferred into the system per
unit mass, because
s,
Q,,,
=
js4
T dS
-
I"
Td
S
s>
(2-158)
(lex1
continues
on
page
226)

6
F
3
CD
1
E
5.
=I
(0
CD
09
Table
2-1
9
g
Summary
of
Thermodynamic Relations (Basis: Unit mass
of
Fluid)
Common Name Derived Relationships
Differential Equation Among Variables
E
Function or Definition or Terminology
m
Heat Capacity at Constant Pressure
6Qp
=
CpdT
Heat Capacity at Constant Volume
6Qv
=
CvdT
AU=Q-W
Heat Capacity Ratio
Internal Energy
(First
Law
of
Thermodynamics)
dU
=
TdS
-
PdV
R
C,
-
C,
=
-
lldeal Gas(
4
(Z)
=-P
S
