Лясин Д.Н., Саньков С.Г. Методы и средства защиты компьютерной информации
Подождите немного. Документ загружается.


В отличие от алгоритма шифрования, отправителем здесь является владелец
пары закрытый/открытый ключ. Процедура формирования электронной подписи
sign под сообщением схожа с шифрованием документа, но в степень закрытого
ключа d по вычету n возводится не само сообщение или его части, а дайджест
сообщения h. Неотъемлемой частью алгоритмов ЭЦП является хэширование
информации, на рисунке оно обозначено через H(), и это может быть любой из
рассмотренных в главе 2.5 алгоритмов хэширования.
Сообщение m с подписью sign будет однозначно аутентифицировано.
Авторство сообщения может быть установлено и доказано по паре ключей (d, e) с
использованием сертификации по схеме, описанной в 3.2. Злоумышленник не
сможет подменить сообщение m (точнее, ему будет очень трудно это сделать),
поскольку ему необходимо вместо сообщения m подставить другое сообщение m
’
,
удовлетворяющее его и имеющее такое же значение хэш-функции, что и у m, что
является на сегодня вычислительно трудной задачей. По этой же причине
70
Отправитель
Получатель
Генерация ключей
Выбрать простые p и q
Вычислить n=p*q
Выбрать случайное e такое,
что: (e,(p-1)(q-1))=1
Найти с помощью
алгоритма Евклида d такое,
что:
ed
1 mod (p-1)(q-1)
Открытый
ключ (e,n)
Закрытый ключ d
h=sign
e
mod n
c=m
e
mod n
Письмо с ЭЦП
(m, sign)
sign=h
d
mod n
Рис.4.1. Схема ЭЦП на основе алгоритма RSA
Сообщение m
h=H(m)
h=H(m)
да
ЭЦП верна
злоумышленник не сможет применить перехваченную подпись sign для подписи
другого документа, поскольку для другого документа будет получено иное значение
хэш-функции h, а оно лежит в основе подписи. Таким образом, все необходимые
свойства подписи описанным алгоритмом обеспечиваются, что же касается
криптостойкости метода ЭЦП, то она определяется криптостойкостью
используемого асимметричного криптографического метода и функции
однонаправленного шифрования. Необходимо отметить также, что само сообщение
m передается в открытом виде. Для того, чтобы обеспечить конфиденциальность
передаваемой в нем информации, требуется использование дополнительного
шифрования по симметричной или асимметричной схеме (при этом шифрование на
ключе d конфиденциальности не обеспечит, поскольку сообщение может быть
расшифровано открытым ключом e).
Очень популярными являются схемы ЭЦП на основе алгоритма ЭльГемаля,
что обусловлено как надлежащей стойкостью алгоритма, так и лучшей по
сравнению с RSA скоростью вычислений. В частности, в стандарте национального
института стандартов США DSS (Digital Signature Standard) используется алгоритм
DSA (Digital Signature Algorithm), который является вариацией алгоритма ЭЦП
ЭльГемаля в модификации Шнорра. В алгоритме используются следующие
открытые параметры:
p - простое число в диапазоне от 512 до 1024 бит;
q - 160-битовое простое число, делитель p-1;
v – любое число, v<p-1, такое, что v
(p-1)/q
mod p >1;
g = v
(p-1)/q
mod p;
y=g
x
mod p.
Секретным ключом является любое 160-разрядное число x, x<q.
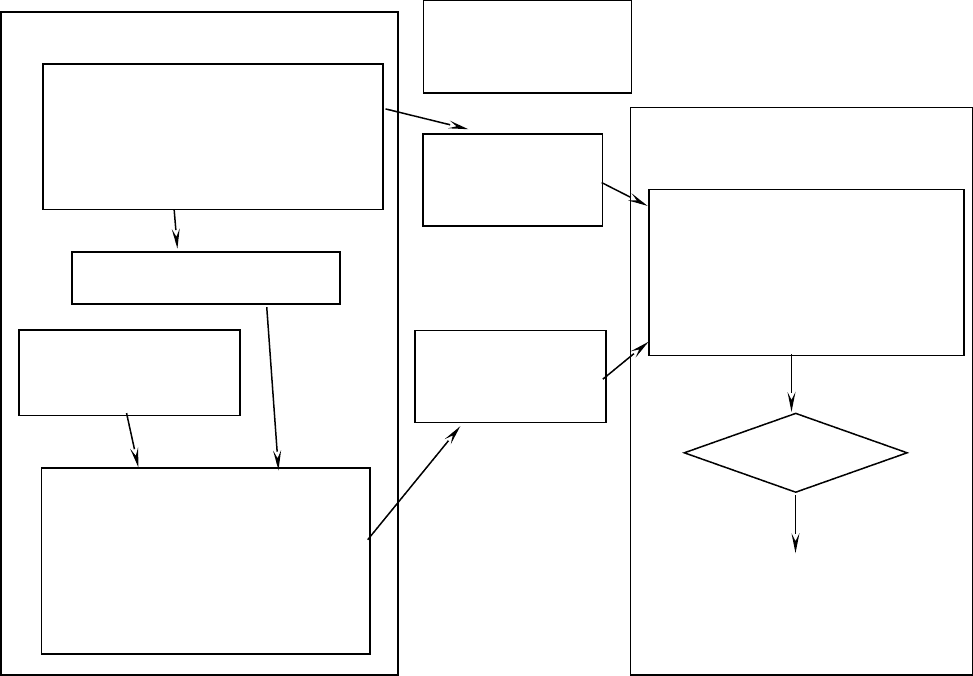
Алгоритм ЭЦП DSA в графической форме представлен на рис.4.2.
71
Существует множество модификаций схемы ЭльГемаля. Одним из типов
модификации стал перенос вычислений в группу, образованную эллиптическими
кривыми. Про эллиптические кривые как математический аппарат реализации
асимметричных криптоалгоритмов уже шла речь в главе 2.4.2. Рассмотрим свойства
эллиптических кривых подробнее.
Для практического применения в криптографии используются эллиптические
кривые (ЭК), заданные над полями Галуа. Пусть задано простое число p > 3. Тогда
эллиптической кривой E, определенной над простым конечным полем F
p
,
называется множество пар чисел (x, y), x, y
F
p
, которые удовлетворяют тождеству:
y
2
= x
3
+ ax + b mod p,
где a, b
F
p
и (4a
3
+ 27b
2
) 0 mod p. Кроме того, к эллиптической кривой
добавляется бесконечно удаленная точка I. Таким образом, точки, удовлетворяющие
уравнению кривой E, и точка I образуют конечную абелеву группу.
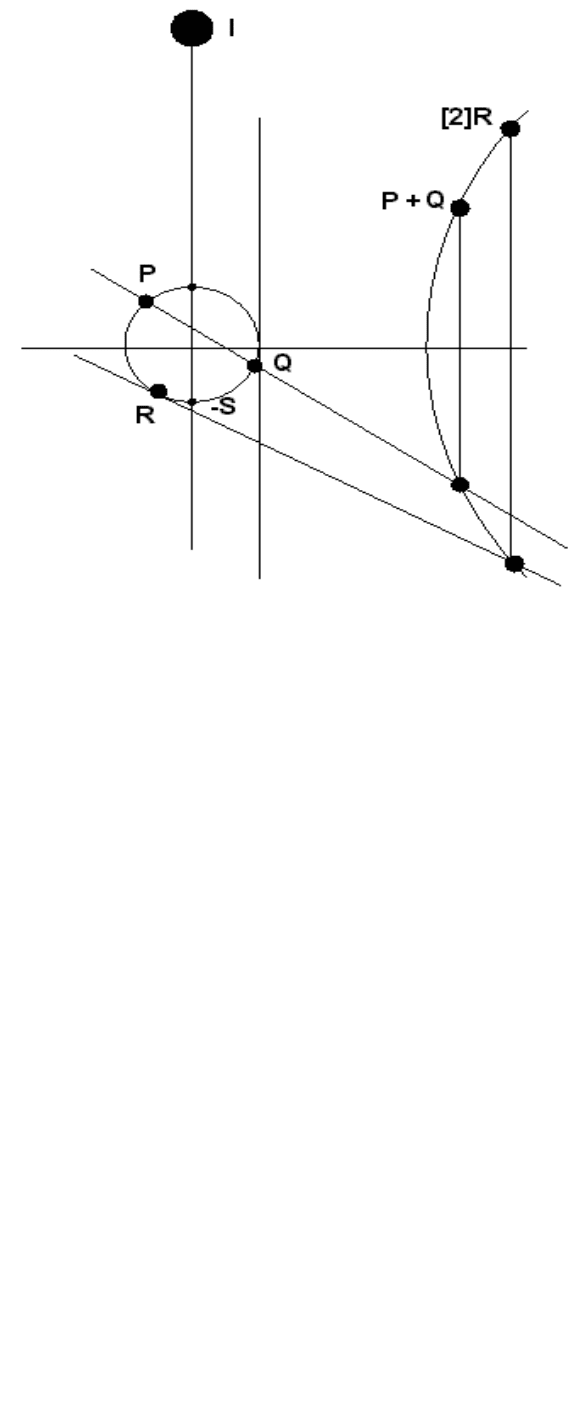
Геометрическое представление эллиптической кривой изображено на рис. 4.3.
72
Отправитель
Получатель
Генерация ключей
Выбрать случайное x
Вычислить
y=g
x
mod p
Открытый
ключ (y)
Закрытый ключ x
w= s
-1
mod q
u
1
= (H(m)w) mod q
u
2
= (rw) mod q
a = ((g
u1
g
u2
) mod p) mod q
Письмо с ЭЦП
(m,r,s)
Формирование подписи
выбрать случайное k<q
r=(g
k
mod p) mod q
s=( (h+xr)/k) mod q
Рис.4.2. Схема алгоритма ЭЦП DSA
Открытые
параметры
(p,q,v)
Сообщение m
h=H(m)
a=r
да
ЭЦП верна
Для точек эллиптической кривой определена операция сложения. Для двух
точек, принадлежащих кривой E, P(x
p
,y
p
) и Q(x
q
,y
q
), точка, являющаяся их суммой,
также будет лежать на эллиптической кривой. Координаты точки S=P+Q
определяются следующими выражениями:
pxxyyk
pqpq
mod))/()((
pxxkx
qps
mod)(
2
pyxxky
pqps
mod))((
Точку S можно получить графически путем несложных построений. Для этого
на графике проводится прямая через точки P и Q, и точка пересечения этой прямой с
ЭК зеркально отображается относительно оси OX (см. рис 4.3).
Если точки P и Q совпадают, то мы получаем точку S=2*Q. Тогда ее
координаты определяются иначе:
pyaxk
qq
mod))*2/()*3((
2
pxkx
qs
mod)2(
2
pyxxky
psqs
mod))((
73
Рис. 4.3. График эллиптической кривой
Графически удвоение точки можно получить, построив касательную к точке и
отразив точку пересечения касательной с эллиптической кривой относительно оси
OX (см. точки R и 2R на рис.4.3). Отсюда очевидно, что можно определить
операцию умножения некоторой точки эллиптической кривой на целое число ,
которая позволяет определить точку Q = k*P (точка P, умноженная на целое число k,
обращается в точку Q). Скалярное умножение осуществляется посредством
нескольких комбинаций сложения и удвоения точек эллиптической кривой.
Например, точка 25*P может быть представлена, как 25*P = 2*(2*(2*(2*P)) +
2*(2*(2*P))) + P. С операцией умножения точки ЭК на целое число напрямую
связана идея, надёжность и криптостойкость эллиптической криптографии. Дело в
том, что задача ECDLP (Elliptic Curve Discrete Logarithm Problem - задача
дискретного логарифма на эллиптической кривой), суть которой заключается в
отыскании целого числа k по известным точкам P и Q = k*P, является
трудноразрешимой. Помимо уравнения, важным параметром кривой является
базисная (генерирующая) точка G, выбираемая для каждой кривой отдельно.
Секретным ключом в соответствии с технологией ЭК является большое случайное
число k, а сообщаемым открытым ключом - произведение k на базисную точку G.
На криптостойкость алгоритма существенное влияние оказывает правильный
выбор как самой кривой (коэффициентов а, b, p) , так и базисной точки G.
Не каждая кривая обеспечивает требуемую криптостойкость, и для некоторых
из них задача ECDLP решается довольно эффективно. Поскольку неудачный выбор
кривой может повлечь за собой снижение обеспечиваемого уровня безопасности,
организации по стандартизации выделяют целые блоки кривых, обладающих
необходимой надёжностью. Использование стандартизированных кривых
рекомендуется и потому, что становится возможной лучшая совместимость между
различными реализациями протоколов информационной безопасности.
Выбор базисной точки обусловлен тем соображением, чтобы ее порядок был
достаточно большим 2
254
< q < 2
256
. Точка P
E называется точкой порядка q, если
qP=I.
74
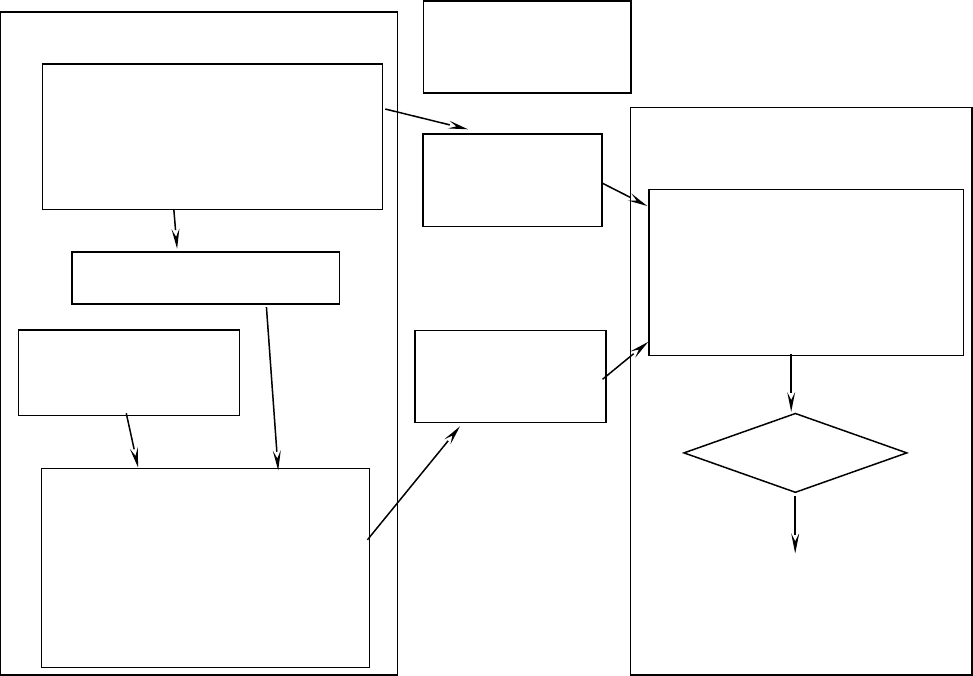
На эллиптических кривых построен алгоритм проверки ЭЦП ГОСТ Р 34.10 –
2001, являющийся на сегодня стандартом РФ в области ЭЦП. Схема этого
алгоритма приведена на рис. 4.4.
Основным достоинством криптосистем на основе ЭК является то, что они
обеспечивают надежность, адекватную классическим криптосистемам (RSA,
ЭльГемаль) на существенно меньших по длине ключах, что положительно
отражается на времени кодирования и декодирования. Криптосистемы цифровой
подписи на основе эллиптических кривых с длиной ключа 160 бит имеют
одинаковую стойкость с криптосистемами DSA и Эль-Гамаля с длиной ключа 1024
бита. Ожидается, что в ближайшем будущем данные системы займут
доминирующее положение в криптографии с открытым ключом. Однако, это
повлечет более серьезные исследования свойств этих криптоалгоритмов, что может
75
Отправитель
Получатель
Генерация ключей
Выбрать случайное d
Вычислить
Q=d*P
Открытый
ключ (Q)
Закрытый ключ d
h=H(
m)
u
1
= s/h mod q
u
2
= (-r)/h mod q
R = КоординатаХ(u
1
P+u
2
Q)
Письмо с ЭЦП
(m,r,s)
Формирование подписи
Выбрать случайное k
r=КоординатаX(k*P)
s=( (rd+kh)) mod q
Рис.4.2. Схема алгоритма ЭЦП ГОСТ Р 34.10-2001
Открытый
параметр (P)
Сообщение m
h=H(m)
R=r
да
ЭЦП верна
привести к появлению новых, более эффективных алгоритмов решения проблемы
дискретного логарифма в группе точек эллиптических кривых.
Еще одним подходом к формированию ЭЦП является использование
симметричных алгоритмов шифрования. Однако, известные на сегодня алгоритмы
этого класса представляют скорее теоретический интерес, поскольку эффективность
их реализации по времени или по объему требуемых вычислений очень невысока.
Например, предложенная Диффи и Хелманом система ЭЦП на симметричном
шифре позволяет подписывать только один бит информации, что на практике
потребует формирования отдельной подписи для каждого бита передаваемого
сообщения, причем подпись бита имеет размер ключа блочного шифра, и каждый
новый бит требует генерации своего ключа подписи. Поэтому системы подобного
класса пока не нашли широкого применения.
Вывод
Электронная цифровая подпись – это эффективное средство защиты
информации от модификации, которое переносит свойства реальной подписи под
документом в область электронного документооборота. В основу ЭЦП положены
такие криптографические методы, как асимметричное шифрование и хэш-функции.
76
5. Основы сетевой безопасности
Бурное развитие сети Интернет привело к появлению множества
дополнительных информационных угроз. Если при работе в локальной сети
существует возможность унификации программной конфигурации для каждой
рабочей станции и используемых в сети протоколов, централизации
администрирования сетью, то глобальная сеть представляет собой
неподконтрольную и очень часто агрессивную информационную среду, в которой
существует ряд специфичных угроз, с которыми нельзя бороться описанными выше
способами. Для противодействия сетевым атакам используются специальные
аппаратные, программные, алгоритмические методы защиты, о которых пойдет речь
в этой главе.
5.1. Угрозы безопасности в глобальных сетях
Одной из основных причин уязвимости информационных систем в сети
Интернет являются слабости сетевого протокола IP стека протоколов TCP/IP,
который служит основой сетевых коммуникаций. При проектировании этого
протокола на заре развития Интернет проблемы безопасности стояли не так остро, и
поэтому внимания защищенности протокола практически не уделялось. В
настоящее время ведутся разработки новой версии протокола – IPv6, который, как
ожидается, будет содержать встроенные механизмы защиты и поможет снять
многие проблемы. Рассмотрим основные сетевые угрозы.
Атаки типа «отказ в обслуживании» (denial of service, DoS ). Под этим
названием объединены методы, призванные расстроить работу некоторого сетевого
устройства путем перегрузки какого-либо ограниченного ресурса, отказа
устройства, изменения его настроек. Ограниченными ресурсами являются
оперативная память, емкость жесткого диска, процессорное время. Типичная DoS
атака представляет собой генерацию большого потока сетевых пакетов, которые не
успевают обрабатываться сетевыми серверами, что приводит либо к отказам в их
работе, либо к невозможности обрабатывать запросы обычных пользователей. В
77
качестве примера DoS атаки можно привести атаку SYN flooding, когда
злоумышленник отправляет на атакуемый компьютер множество TCP-пакетов с
установленным флагом SYN и несуществующим адресом отправителя. Атакуемый
компьютер в ответ на каждый такой пакет создает внутренние структуры данных,
необходимые для поддержки соединения и отправляет ответный пакет для
подтверждения соединения. Так как в качестве адреса отправителя был указан
несуществующий адрес, то ответа на свой пакет атакуемый компьютер не дождется,
а память под внутренние структуры данных будут некоторое время
зарезервированы. При большом количестве атакующих пакетов память атакуемого
компьютера может закончиться, что приведет к его отказу. Для предотвращения
подобных атак используются интеллектуальные фильтры пакетов, в момент
возникновения атаки можно динамически уменьшать время ожидания ответа на
пакет. Особенно разрушительными являются распределенные DoS-атаки (distributed
DoS, DDoS). При реализации атаки данного типа злоумышленник сначала должен
получить доступ ко множеству слабо защищенных компьютеров, подсоединенных к
Интернет и установить на них специальное программное обеспечение DDoS.
Удаленный компьютер с установленным программным обеспечение DDoS
называется агентом. По команде с компьютера злоумышленника агенты начинают
передавать сетевые пакеты на атакуемый компьютер. Агенты могут направить ICMP
запросы на широковещательный адрес (Smurf атаки), поддельные HTTP запросы,
фрагментированные пакеты или случайный трафик. Атака может быть направлена
на любое сетевое устройство: маршрутизаторы (что эффективно блокирует всю
сеть), серверы (Web, mail, DNS), или специфичные компьютеры (firewalls, IDS). В
результате атаки (а несколько сотен машин могут создать трафик в несколько
гигабайт) атакуемый компьютер либо полностью перестанет обрабатывать запросы,
либо будет делать это очень медленно.
Очень распространенными являются атаки с использованием протокола
ICMP. Протокол управляющих сообщений ICMP (Internet Control Message Protocol)
носит вспомогательный характер (популярная утилита ping использует этот
протокол). Протокол ICMP не содержит методов аутентификации источника
сообщения, что активно используется злоумышленниками. Например, для
78
блокировки обслуживания используются icmp-сообщения “time exceeded”
(превышено время) или “destination unreachable” (адресат недоступен). Первое
сообщение означает, что предел, указанный в поле TTL заголовка пакета, превышен.
Такое может произойти из-за зацикливания пакетов или когда адресат расположен
очень далеко. Сообщение “destination unreachable” имеет несколько значений. Но
все они означают, что нет способа благополучно доставить пакет адресату. Оба
сообщения вынуждают адресата немедленно прервать соединение. Именно эту цель
может преследовать злоумышленник, посылая такое сообщение одному из
участников взаимодействия. Протокол ICMP может использоваться и для перехвата
пакетов. ICMP-сообщение “redirect” обычно используется внешними портами сети в
случаях, когда какая-то ЭВМ полагает, что адресат находится вне локальной сети и
направляет пакеты, адресованные ему, через внешний порт. Злоумышленник может
послать ICMP-сообщение “redirect” и вынудить другую ЭВМ посылать пакеты через
узел, указанный злоумышленником.
Популярными являются также атаки на серверы некоторых сетевых служб
(Web, mail), когда из-за ошибок в программном обеспечении запросы определенной
конфигурации способны вызвать ошибки типа переполнение буфера, предоставить
злоумышленнику доступ с правами администратора.
Важным аспектом безопасности является обеспечение конфиденциальности
сетевого трафика, поскольку пакеты сообщения могут быть перехвачены на любом
промежуточном узле по пути следования к получателю, а встроенных средств
шифрования классический протокол IP не предоставляет.
Глобальная сеть является благоприятной средой для распространения вирусов
и «троянских коней». Развитие Интернет привело к появлению такого феномена как
вирусы – черви. Остановимся подробнее на сетевом черве Klez. Этот экземпляр
заражает компьютер через ошибку в почтовой программе Outlook: когда
пользователь пытается прочитать письмо, содержащее вирус, Klez инфицирует
систему. После попадания в ОС сетевой червь сканирует жесткие диски, ищет
электронные адреса и рассылает на них письма, прикрепляя свое тело в качестве
вложения, создавая очень большой исходящий трафик. Таким образом, скорость
распространения сетевого червя становилась очень высокой. Эту же схему
79
