Лупал А.М. Теория автоматов (часть 2)
Подождите немного. Документ загружается.

74
7. ÝËÅÌÅÍÒÀÐÍÛÅ ÀÂÒÎÌÀÒÛ
Èç òåîðåìû î ñòðóêòóðíîé ïîëíîòå ñëåäóåò, ÷òî äëÿ ñòðóêòóðíîé
ïîëíîòû ñèñòåìû ýëåìåíòàðíûõ àâòîìàòîâ íåîáõîäèìî âêëþ÷åíèå â
íåå ýëåìåíòàðíûõ àâòîìàòîâ Ìóðà ñ ïîëíîé ñèñòåìîé ïåðåõîäîâ è ïîë-
íîé ñèñòåìîé âûõîäîâ. Òåîðåòè÷åñêè òàêèå àâòîìàòû, ïðåäñòàâëÿþ-
ùèå ñîáîé ýëåìåíòû ïàìÿòè, ìîãóò îáëàäàòü ëþáûì ÷èñëîì âíóòðåí-
íèõ ñîñòîÿíèé, îäíàêî èñõîäÿ èç ðåàëüíûõ âîçìîæíîñòåé ñîâðåìåííîé
òåõíîëîãèè, îïòèìàëüíûì ÷èñëîì ñîñòîÿíèé ýëåìåíòàðíîãî àâòîìàòà
ÿâëÿåòñÿ äâà, à ñòðóêòóðíûé àëôàâèòîì ñîñòîÿíèé àâòîìàòà ÿâëÿåòñÿ
äâîè÷íûé àëôàâèò.
Ðàññìîòðèì íåêîòîðóþ îáîáùåííóþ ìîäåëü ýëåìåíòàðíîãî àâòî-
ìàòà, ïðåäñòàâëÿþùóþ ñîáîé àâòîìàò Ìóðà, çàäàííûé ñëåäóþùèì ìíî-
æåñòâîì ýëåìåíòîâ:
A = {C, V, δ, λ, c
1
},
ãäå C = {c1, c2} àëôàâèò ñîñòîÿíèé; V = {v
1
, v
2
, v
3
, v
4
} âõîäíîé àëôà-
âèò, ïðè÷åì v
1
ñèãíàë, íå ìåíÿþùèé èñõîäíîå ñîñòîÿíèå àâòîìàòà,
òàêîé, ÷òî c
1
= δ{c
1
, v
1
}, c
2
=δ{c
2
, v
1
}; v
2
ñèãíàë, ïåðåâîäÿùèé àâòîìàò
â ñîñòîÿíèå, ïðîòèâîïîëîæíîå èñõîäíîìó, òàêîé, ÷òî c
1
= δ{c
2
, v
2
},
c
2
=δ{c
1
, v
2
}; v
3
ñèãíàë, âñåãäà ïåðåâîäÿùèé àâòîìàò â ñîñòîÿíèå c
1
,
òàêîé, ÷òî c
1
= δ{c
1
, v
3
}, c
1
=δ{c
2
, v
3
}; v
4
ñèãíàë, âñåãäà ïåðåâîäÿùèé
àâòîìàò â ñîñòîÿíèå v
4
, òàêîé, ÷òî c
2
= δ{c
1
, v
4
}, c
2
=δ{c
2
, v
4
}; c
1
íà÷àëüíîå ñîñòîÿíèå; δ è λ ôóíêöèÿ ïåðåõîäîâ è ôóíêöèÿ âûõîäîâ,
îïðåäåëÿåìûå ñ ïîìîùüþ ãðàôà ïåðåõîäîâ (ðèñ. 7.1).
Ïîñêîëüêó â àâòîìàòå Ìóðà ñ ïîëíîé ñèñòåìîé âûõîäîâ âíóòðåí-
íèå ñîñòîÿíèÿ îòîæäåñòâëÿþòñÿ ñ âûõîäíûìè ñèãíàëàìè, äëÿ èõ îáî-
çíà÷åíèÿ èñïîëüçîâàí îäèí è òîò æå àëôàâèò (â äàííîì ñëó÷àå àëôà-
âèò Ñ).
Íà áàçå ðàññìîòðåííîé ìîäåëè ìîæíî ïîñòðîèòü 16 ýëåìåíòîâ ïàìÿ-
òè ñ ðàçëè÷íûìè êîìáèíàöèÿìè àáñòðàêòíûõ âõîäíûõ ñèãíàëîâ, íî òîëüêî
ñåìü èç íèõ áóäóò îáëàäàòü ïîëíîé ñèñòå-
ìîé ïåðåõîäîâ è ïîëíîé ñèñòåìîé âûõîäîâ.
Àâòîìàòû ñ îäíèì âõîäíûì ñèãíàëîì íå
ìîãóò îáëàäàòü ïîëíîòîé, ïîñêîëüêó äëÿ
ýòîãî íåîáõîäèìî, ÷òîáû ÷èñëî àáñòðàêò-
íûõ âõîäíûõ ñèãíàëîâ àâòîìàòà áûëî, ïî
êðàéíåé ìåðå, íå ìåíüøå ÷èñëà åãî ñîñòî-
v
2
v
2
v
3
v
4
v
1
v
1
v
4
v
3
c
2
c
1
Ðèñ. 7.1
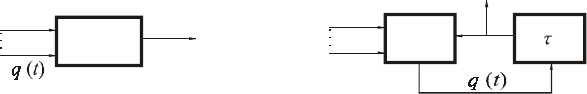
75
ÿíèé. Èç àâòîìàòîâ ñ äâóìÿ âõîäíûìè ñèãíàëàìè òîëüêî äâà èç øåñòè
óäîâëåòâîðÿþò ïðèâåäåííîìó òðåáîâàíèþ. Ýòî àâòîìàòû, â êîòîðûõ â
êà÷åñòâå âõîäíîãî àëôàâèòà èñïîëüçóåòñÿ àëôàâèò V
1
= {v
3
, v
4
} (àâòî-
ìàò A
1
) è àëôàâèò V
2
= {v
1
, v
2
} (àâòîìàò À
2
). Ïîëíûì òàêæå ÿâëÿåòñÿ
àâòîìàò A
3
ñ òðåìÿ âõîäíûìè ñèãíàëàìè ñ àëôàâèòîì V
3
= {v
1
, v
3
, v
4
}, à
òàêæå àâòîìàò A
4
ñ ÷åòûðüìÿ âõîäíûìè ñèãíàëàìè.
Ïåðå÷èñëåííûå ýëåìåíòàðíûå àâòîìàòû è èõ ìîäèôèêàöèè ÿâëÿþò-
ñÿ íàèáîëåå øèðîêî èñïîëüçóåìûìè ýëåìåíòàìè ïàìÿòè â ñîâðåìåí-
íûõ öèôðîâûõ óñòðîéñòâàõ.
Ðàññìîòðèì ñòðóêòóðíûå îñîáåííîñòè ýòèõ àâòîìàòîâ, ñ÷èòàÿ,
÷òî ëþáîé ñòðóêòóðíûé ýëåìåíòàðíûé àâòîìàò ñ äâóìÿ ñîñòîÿíèÿ-
ìè èìååò âèä, ïðåäñòàâëåííûé íà ðèñ. 7.2. Ïîñêîëüêó ýòîò àâòîìàò
ÿâëÿåòñÿ àâòîìàòîì Ìóðà, âûõîäíîé ñèãíàë çàäåðæèâàåòñÿ îòíîñè-
òåëüíî âõîäíîãî íà îäèí òàêò àâòîìàòíîãî âðåìåíè. Â ñîîòâåòñòâèè
ñ òåîðåìîé î ñòðóêòóðíîé ïîëíîòå ñõåìó ëþáîãî ñòðóêòóðíîãî ýëå-
ìåíòàðíîãî àâòîìàòà ìîæíî ïðåäñòàâèòü ñîñòîÿùåé èç äâóõ ÷àñòåé:
çàïîìèíàþùåé ÷àñòè, â êîòîðîé íå ïðîèçâîäèòñÿ ëîãè÷åñêîå ïðåîá-
ðàçîâàíèå èíôîðìàöèè (ýëåìåíò çàäåðæêè ñèãíàëà t) è êîìáèíàöèîí-
íîé ñõåìû (ðèñ. 7.3). Ïðèâåäåííàÿ íà ðèñ. 7.3 ôóíêöèÿ âîçáóæäåíèÿ
q
ýë
(t) ïðåäñòàâëÿåò ñîáîé ñîáñòâåííóþ ôóíêöèþ âîçáóæäåíèÿ ýëå-
ìåíòà ïàìÿòè. Ñëåäóåò çàìåòèòü, ÷òî äëÿ çàäàíèÿ ñòðóêòóðíîãî ýëå-
ìåíòàðíîãî àâòîìàòà öåëåñîîáðàçíî èñïîëüçîâàòü ìàòðèöó ïåðåõî-
äîâ, ýëåìåíòàìè êîòîðîé ÿâëÿþòñÿ çíà÷åíèÿ ñòðóêòóðíûõ âõîäíûõ
ñèãíàëîâ àâòîìàòà, çàäàííûå íà óïîðÿäî÷åííûõ ïàðàõ ñîñòîÿíèé
ñòðóêòóðíîãî àâòîìàòà è ïåðåâîäÿùèå ïåðâûé ýëåìåíò ñîîòâåòñòâó-
þùåé ïàðû âî âòîðîé.
Äëÿ ðàññìàòðèâàåìîé ìîäåëè ñóùåñòâóåò ÷åòûðå âîçìîæíûõ ïåðå-
õîäà ñòðóêòóðíûõ ñîñòîÿíèé: 0→0, 0→1, 1→0, 1→1. Äëÿ êàæäîãî èç
ýòèõ ïåðåõîäîâ íàéäåòñÿ çíà÷åíèå âõîäíîãî ñèãíàëà, âûçûâàþùåãî çà-
äàííûé ïåðåõîä. Òîãäà çàêîí ôóíêöèîíèðîâàíèÿ ýëåìåíòàðíîãî àâòîìà-
Q
Qt+(1)
()n
q t()
(0)
ÊÑ
Qt+(1)
q t()
()n
ýë
q t()
(0)
Ðèñ. 7.2
Ðèñ. 7.3

76
òà, èìåþùåãî m ýëåìåíòàðíûõ âõîäíûõ êàíàëîâ, ìîæíî îïèñàòü ñëåäó-
þùåé ìàòðèöåé ïåðåõîäîâ:
Qt Qt+
12
12
00 00 00 00
12
01 01 01 01
12
10 10 10 10
12
11 11 11 11
km
km
km
km
km
qq q q
bb b b
bb b b
bb b b
bb b b
=
M
LL
LL
LL
LL
ãäå Q(t) è Q(t+1) ñîñòîÿíèÿ ñòðóêòóðíîãî ýëåìåíòàðíîãî àâòîìàòà â
ïîñëåäîâàòåëüíûå ìîìåíòû àâòîìàòíîãî âðåìåíè. Êîëè÷åñòâî ñòðîê
ìàòðèöû M äëÿ ëþáîãî ýëåìåíòàðíîãî àâòîìàòà ñ ïîëíîé ñèñòåìîé
ïåðåõîäîâ ðàâíî ÷åòûðåì, à êîëè÷åñòâî ñòîëáöîâ ðàâíî ÷èñëó âõîäíûõ
êàíàëîâ.
Ýëåìåíò ìàòðèöû b
k
ij
ïðåäñòàâëÿåò ñîáîé çíà÷åíèå âõîäíîãî ñèãíà-
ëà q
k
, ïîä äåéñòâèåì êîòîðîãî àâòîìàò ïåðåõîäèò èç ñîñòîÿíèÿ i â ñî-
ñòîÿíèå j. Ïðè ýòîì êàæäûé ýëåìåíò ìàòðèöû ìîæåò áûòü ðàâåí 1, 0
èëè íåîïðåäåëåííîìó êîýôôèöèåíòó b. Íåîïðåäåëåííûå êîýôôèöèåíòû
çàïèñûâàþòñÿ â òîì ñëó÷àå, êîãäà çíà÷åíèÿ ñèãíàëîâ, ïîñòóïàþùèõ íà
äàííûé âõîä, íå âëèÿþò íà ðàññìàòðèâàåìûé ïåðåõîä.
7.1. Ýëåìåíòàðíûå àâòîìàòû ñ äâóìÿ âõîäíûìè ñèãíàëàìè
Äëÿ ïðîâåäåíèÿ îïåðàöèè ñòðóêòóðíîãî ñèíòåçà ñ öåëüþ ïîëó÷å-
íèÿ ñòðóêòóðíîé ñõåìû ýëåìåíòàðíîãî àâòîìàòà A
1
, ãðàô ïåðåõîäîâ
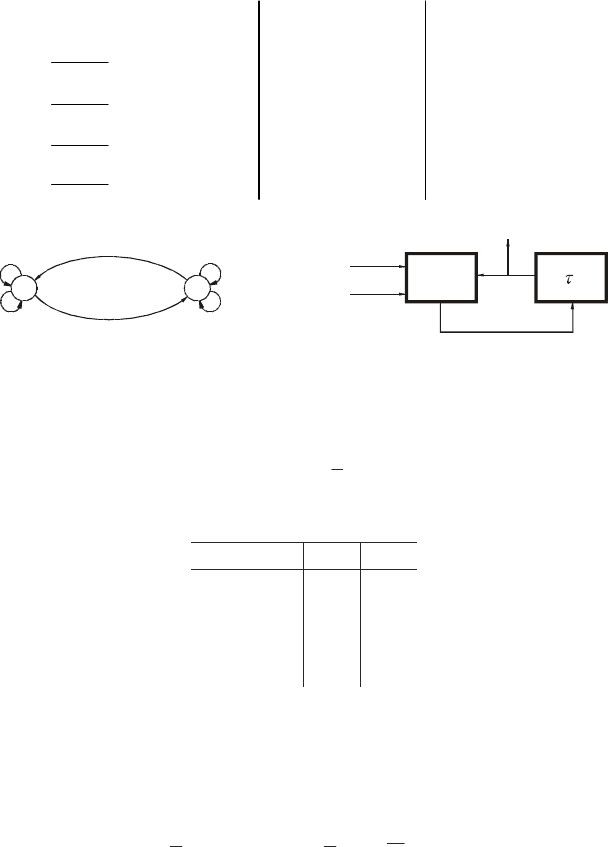
êîòîðîãî ïðèâåäåí íà ðèñ. 7.4, íåîáõîäèìî ïðîâåñòè îïåðàöèþ êîäè-
ðîâàíèÿ ñîñòîÿíèé àâòîìàòà è åãî âõîäíûõ ñèãíàëîâ. Ïîñêîëüêó àá-
ñòðàêòíîìó àâòîìàòó ñ äâóìÿ âõîäíûìè è äâóìÿ âûõîäíûìè ñèãíà-
ëàìè ñîîòâåòñòâóåò ñòðóêòóðíûé àâòîìàò ñ îäíèì âõîäíûì è îäíèì
âûõîäíûì êàíàëîì, ðåçóëüòàò îïåðàöèè êîäèðîâàíèÿ âõîäíûõ ñèãíà-
ëîâ è ñîñòîÿíèé áóäåò èìåòü âèä, ïðåäñòàâëåííûé ñîîòâåòñòâåííî â
òàáë. 7.1 è 7.2.
Òàáëèöà 7.1 Òàáëèöà 7.2
LG
L
!
L
"
?3
?
?

77
Íà îñíîâàíèè ðèñ.7.4 è òàáë.7.1 è 7.2 ìîæíî ñîñòàâèòü êîäèðîâàí-
íóþ òàáëèöó ïåðåõîäîâ ñòðóêòóðíîãî ýëåìåíòàðíîãî àâòîìàòà A
1
(òàáë.7.3), êîäèðîâàííûé ãðàô ïåðåõîäîâ (ðèñ. 7.5), à òàêæå åãî ìàòðèöó
ïåðåõîäîâ
Qt Qt+
0
1
0
1
q
=
M
(7.1)
Ðàññìàòðèâàÿ òàáë. 7.3 è ìàòðèöó (7.1), ìîæíî çàêëþ÷èòü, ÷òî
çíà÷åíèå ñîñòîÿíèÿ àâòîìàòà Q(t+1) è ñîîòâåòñòâóþùåãî åìó âû-
õîäíîãî ñèãíàëà îïðåäåëÿþòñÿ çíà÷åíèåì âõîäíîãî ñèãíàëà q(t) è íå
çàâèñÿò îò ñîñòîÿíèÿ àâòîìàòà Q(t), ò. å. Q(t+1) = q(t). Â òî æå âðåìÿ
íà îñíîâàíèè àíàëèçà ñõåìû, ïðèâåäåííîé íà ðèñ. 7.3, ìîæíî ñäå-
ëàòü âûâîä, ÷òî
Q(t+1) = q
ýë
(t).
Ñëåäîâàòåëüíî,
q(t) = q
ýë
(t)
è êîìáèíàöèîííàÿ ñõåìà â òàêîì ñëó÷àå ñòàíîâèòñÿ äëÿ àâòîìàòà A
1
èçëèøíåé.
Òàêèì îáðàçîì, ñõåìà àâòîìàòà ïðèîáðåòàåò âèä, ïðåäñòàâëåííûé
íà ðèñ. 7.6, à ñàì àâòîìàò A
1
ïðåäñòàâëÿåò ñîáîé ýëåìåíò çàäåðæêè è
íàçûâàåòñÿ òðèããåðîì òèïà D (delay çàäåðæêà).
v
3
v
4
v
4
v
3
c
2
c
1
1
1
00
0
Qt+(1)
qt()
Ðèñ.7.4
Ðèñ.7.5
Ðèñ. 7.6

78
Òàáëèöà 7.3
Ïåðåéäåì ê ðàññìîòðåíèþ ñõåìû ñòðóêòóðíîãî ýëåìåíòàðíîãî
àâòîìàòà A
2
, ãðàô ïåðåõîäîâ êîòîðîãî ïðåäñòàâëåí íà ðèñ. 7.7. Â ïðî-
öåññå êîäèðîâàíèÿ âõîäíûõ ñèãíàëîâ è ñîñòîÿíèé àâòîìàòà ìîæíî
ñôîðìèðîâàòü ñîîòâåòñòâåííî òàáë. 7.4 è 7.2, èç êîòîðûõ ñëåäóåò,
÷òî ñòðóêòóðíûé àâòîìàò A
2
èìååò òàê æå, êàê è àâòîìàò A
1
, òîëüêî
îäèí âõîäíîé êàíàë. Íà áàçå ãðàôà ïåðåõîäîâ àâòîìàòà A
2
è òàáë. 7.4
è 7.2 ïîëó÷àåì êîäèðîâàííûé ãðàô ïåðåõîäîâ (ðèñ. 7.8), êîäèðîâàí-
íóþ òàáëèöó ïåðåõîäîâ (òàáë. 7.5) è ìàòðèöó ïåðåõîäîâ (7.2) àâòî-
ìàòà A
2
.
Òàáëèöà 7.4 Òàáëèöà 7.5
Ïðîâåäåì îïåðàöèþ ñèíòåçà ñòðóêòóðíîé ñõåìû àâòîìàòà A
2
. Èç
òàáë. 7.5 ìîæíî ïîëó÷èòü ëîãè÷åñêîå âûðàæåíèå äëÿ ñîñòîÿíèÿ è ñîîò-
âåòñòâóþùåãî åìó âûõîäíîãî ñèãíàëà àâòîìàòà
Q(t+1) = q(t)
Q
(t) ∨
q
(t)Q(t) = q(t) ⊕ Q(t).
Ïîñêîëüêó â ëþáîì ýëåìåíòàðíîì àâòîìàòå
Q(t+1) = q
ýë
(t),
ìîæíî çàïèñàòü
q
ýë
(t) = q(t) ⊕ Q(t).
v
2
v
2
v
1
v
1
c
2
c
1
Ðèñ.7.7
G
LG
L
L
G
1
1
0
0
0
1
Ì2
Q(t+ )1
q(t)
q (t)
ýë
Ðèñ. 7.8
Ðèñ. 7.9

79
Ñëåäîâàòåëüíî, àâòîìàò A
2
ìîæåò áûòü ðåàëèçîâàí íà áàçå ýëåìåí-
òà çàäåðæêè ñ äîáàâëåíèåì êîìáèíàöèîííîé ñõåìû, âûïîëíÿþùåé îïå-
ðàöèþ ñëîæåíèÿ ïî ìîäóëþ 2, êîòîðàÿ ìîæåò áûòü ïîñòðîåíà â ëþáîì
ëîãè÷åñêîì áàçèñå (ðèñ. 7.9). Ýòîò àâòîìàò íàçûâàåòñÿ òðèããåðîì ñî
ñ÷åòíûì âõîäîì èëè òðèããåðîì òèïà T.
7.2. Ýëåìåíòàðíûå àâòîìàòû ñ òðåìÿ âõîäíûìè ñèãíàëàìè
Òàê æå, êàê è äëÿ àâòîìàòîâ ñ äâóìÿ âõîäíûìè ñèãíàëàìè, â ýòîì
ñëó÷àå â çàâèñèìîñòè îò êîìáèíàöèé è êîäèðîâàíèÿ òðåõ èñïîëüçóåìûõ
âõîäíûõ ñèãíàëîâ ìîæíî ñïðîåêòèðîâàòü ðàçëè÷íûå ñòðóêòóðíûå ñõå-
ìû ýëåìåíòàðíûõ àâòîìàòîâ.
Ðàññìîòðèì àâòîìàò A
3
, èñïîëüçóþùèé âõîäíîé àëôàâèò V
3
= {v
1
, v
3
, v
4
},
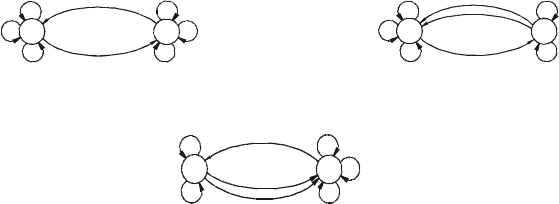
ãðàô ïåðåõîäîâ êîòîðîãî ïðåäñòàâëåí íà ðèñ. 7.10.
Òàáëèöà 7.6
Çàêîäèðóåì ñîñòîÿíèÿ àâòîìàòà A
3
(òàáë. 7.2) è åãî âõîäíûå ñèã-
íàëû. Ïîñêîëüêó àâòîìàò A
3
èìååò òðè àáñòðàêòíûõ âõîäíûõ ñèãíà-
ëà, ÷èñëî åãî ñòðóêòóðíûõ âõîäíûõ êàíàëîâ äîëæíî ðàâíÿòüñÿ äâóì
è ìîæåò áûòü çàêîäèðîâàíî ñïîñîáîì, ïðåäñòàâëåííûì â òàáë. 7.6.
Êîìáèíàöèÿ ñòðóêòóðíûõ âõîäíûõ ñèãíàëîâ {1, 1} ÿâëÿåòñÿ çàïðå-
ùåííîé êîìáèíàöèåé äëÿ äàííîãî òèïà ýëåìåíòàðíîãî àâòîìàòà. Íà
îñíîâàíèè òàáë. 7.2, 7.6 è ðèñ. 7.10 ïîñòðîèì êîäèðîâàííûé ãðàô ïå-
ðåõîäîâ àâòîìàòà A
3
(ðèñ. 7.11), êîäèðîâàííóþ òàáëèöó ïåðåõîäîâ
(òàáë. 7.7) è ìàòðèöó ïåðåõîäîâ (7.3). Ñèìâîë b â ìàòðèöå ïåðåõî-
äîâ îçíà÷àåò áåçðàçëè÷íîå çíà÷åíèå äàííîãî âõîäíîãî ñèãíàëà äëÿ
óêàçàííîãî ïåðåõîäà. Ïðîñëåæèâàÿ ïî òàáë. 7.7 ïåðåõîäû àâòîìàòà
À
3
, ìîæíî óáåäèòüñÿ, ÷òî åäèíè÷íîå çíà÷åíèå ñèãíàëà q
(0)
ïåðåâîäèò
àâòîìàò â íóëåâîå ñîñòîÿíèå íåçàâèñèìî îò çíà÷åíèÿ åãî èñõîäíîãî
ñîñòîÿíèÿ, è, íàîáîðîò, åäèíè÷íîå çíà÷åíèå ñèãíàëà q
(1)
ïåðåâîäèò
àâòîìàò âñåãäà â åäèíè÷íîå ñîñòîÿíèå. Áëàãîäàðÿ ýòîé îñîáåííîñòè
àâòîìàòà A
3
åãî âõîäíûå êàíàëû íàçûâàþòñÿ ñîîòâåòñòâåííî íóëå-
âûì (q
(0)
) è åäèíè÷íûì ( q
(1)
).
Ðèñ. 7.10
v
3
v
4
v
1
v
1
v
4
v
3
c
2
c
1
LG
G
L
L
L
!
80
Qt Qt+
() ()
00
0
01
10
0
qq
b
b
=
M
(7.3)
Ëîãè÷åñêîå âûðàæåíèå äëÿ ôèêöèè q
ýë
àâòîìàòà A
3
ìîæíî ïîëó÷èòü
èç òàáë. 7.7, äîîïðåäåëèâ íåîïðåäåëåííûå ïåðåõîäû åäèíèöàìè. Â ðå-
çóëüòàòå ïîëó÷èì
q
ýë
(t) = Q(t+1) =
q
(0)
(t)Q(t) ∨ q
(1)
(t).
Òàáëèöà 7.7
Ïåðåâåäÿ ïîëó÷åííîå âûðàæåíèå â áàçèñ Øåôôåðà, ïîëó÷èì
q
ýë
(t) = S(S(S(q
(0)
(t)), Q(t)), S(q
(1)
(t)).
Ìîæíî ïîëó÷èòü äðóãîå âûðàæåíèå äëÿ q
ýë
àâòîìàòà À
3
, äîîïðåäåëèâ
çàïðåùåííûå íàáîðû íå åäèíèöàìè, à íóëÿìè. Â ðåçóëüòàòå èìååì
q
ýë
(t) = q
(0)
(t) ∨
q
(1)
(t)
Q
(t). (7.4)
Âçÿâ îòðèöàíèå îò îáåèõ ÷àñòåé âûðàæåíèÿ (7.4) è ïåðåâåäÿ åãî â
áàçèñ Ïèðñà, ïîëó÷èì
q
ýë
(t) = P(q
(0)
(t), P(q
(1)
(t),Q(t))). (7.5)
Ðèñ. 7.11
Ðèñ. 7.12
1
01
01
0000
10
10
0
ÊÑ
Qt+(1)
q t()
(1)
q t()
ýë
q t()
G
G
``
81
Òàêèì îáðàçîì, êîìáèíàöèîííàÿ ñõåìà ýëåìåíòàðíîãî àâòîìàòà
ïðåäñòàâëÿåò ñîáîé ïîñëåäîâàòåëüíîå ñîåäèíåíèå ëèáî ýëåìåíòîâ
Ïèðñà (äëÿ ïðÿìîãî çíà÷åíèÿ âõîäíûõ ñèãíàëîâ), ëèáî äâóõ ýëåìåí-
òîâ Øåôôåðà (äëÿ èíâåðñíîãî çíà÷åíèÿ âõîäíûõ ñèãíàëîâ) è èìååò
äâà âõîäíûõ êàíàëà (ðèñ. 7.12). Ýòîò àâòîìàò ïîëó÷èë íàçâàíèå òðèã-
ãåðà ñ ðàçäåëüíûìè âõîäàìè èëè òðèããåðà òèïà RS (set óñòàíîâèòü;
reset ñáðîñèòü), ãäå ñ ïîìîùüþ R è S îáîçíà÷åíû ñîîòâåòñòâåííî
âõîäû q
(0)
è q
(1)
.
Íàëè÷èå íåîïðåäåëåííûõ ñîñòîÿíèé, îòìå÷åííûõ â òàáë. 7.7 ïðî÷åð-
êàìè, îãðàíè÷èâàåò ôóíêöèîíàëüíûå âîçìîæíîñòè RS-òðèããåðà.  ðÿäå
ñëó÷àåâ òðåáóåòñÿ, ÷òîáû ñîñòîÿíèÿ òðèããåðà áûëè îïðåäåëåíû ïðè âñåõ
êîìáèíàöèÿõ âõîäíûõ ñèãíàëîâ, âêëþ÷àÿ è òå, êîòîðûå çàïðåùåíû äëÿ
RS-òðèããåðà.
Äëÿ ïîñòðîåíèÿ ðàçëè÷íûõ ìîäèôèêàöèé RS-òðèããåðà â ýòîì ñëó÷àå
äåëàåòñÿ äóáëèðîâàíèå îäíîãî èç òðåõ àáñòðàêòíûõ âõîäíûõ ñèãíàëîâ:
v
1
, v
3
èëè v
4
è êîäèðîâàíèå äîïîëíèòåëüíîãî ñèãíàëà ñòðóêòóðíûìè ñèì-
âîëàìè 11. Êàæäàÿ ïîëó÷åííàÿ ïðè ýòîì ðàçíîâèäíîñòü òðèããåðà ñ÷èòà-
åòñÿ ñàìîñòîÿòåëüíûì òèïîì è èìååò ñâîå íàèìåíîâàíèå.
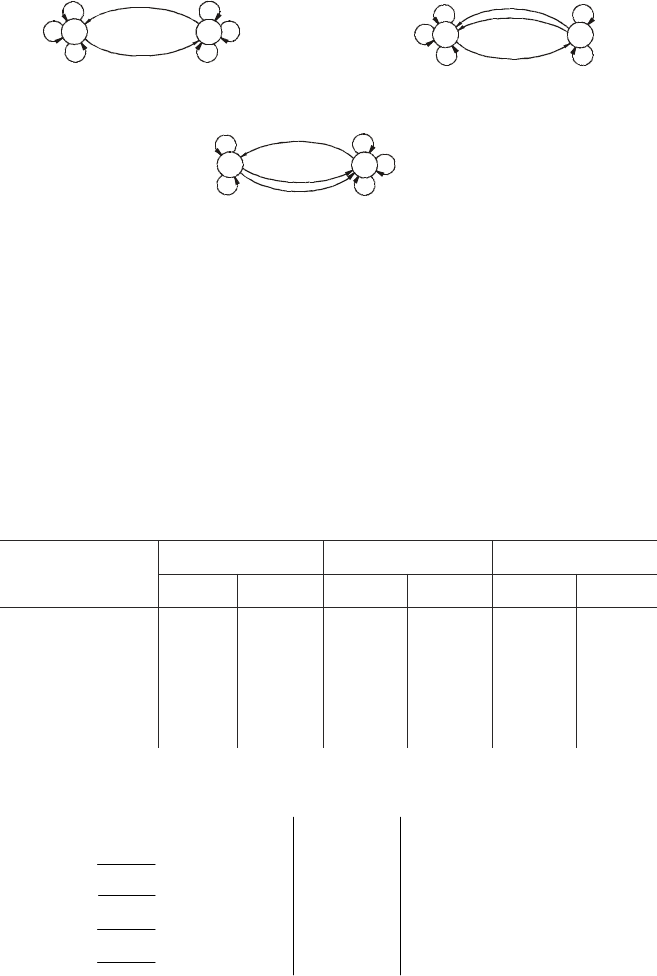
Ðàññìîòðèì ïîëó÷àåìûå òàêèì îáðàçîì àâòîìàòû. Ïåðåõîäû, îñó-
ùåñòâëÿåìûå äîïîëíèòåëüíûìè ñèãíàëàìè v
1
, v
3
èëè v
4
, ïîêàçàíû íà
ãðàôàõ ïåðåõîäîâ àáñòðàêòíûõ àâòîìàòîâ A
4
, A
5
, A
6
ñîîòâåòñòâåííî íà
ðèñ. 7.13, 7.14 è 7.15.
Êîäèðîâàííûå ãðàôû ïåðåõîäîâ, ñîîòâåòñòâóþùèå ïðèâåäåííûì àá-
ñòðàêòíûì àâòîìàòàì, èìåþò âèä, ïðåäñòàâëåííûé íà ðèñ. 7.16, 7.17 è
7.18.
v
3
v
4
v
1
v
1
v'
1
v'
1
v
4
v
3
c
2
c
1
v
3
v
4
v
1
v
1
v'
3
v'
3
v
4
v
3
c
2
c
1
v
4
v
1
v
1
v'
4
v'
4
v
4
v
3
v
3
c
2
c
1
Ðèñ. 7.13
Ðèñ. 7.14
Ðèñ. 7.15
82
Àíàëèçèðóÿ ïåðåõîäû àâòîìàòîâ íà ðèñ. 7.16, 7.17 è 7.18, ìîæíî çà-
ìåòèòü, ÷òî êàæäûé äîïîëíèòåëüíûé ñèãíàë îáåñïå÷èâàåò îäèí èç ÷å-
òûðåõ âîçìîæíûõ ïåðåõîäîâ. Àâòîìàò íà ðèñ. 7.16 ïîä äåéñòâèåì ñèã-
íàëà 11 îñòàåòñÿ â ïðåæíåì ñîñòîÿíèè è íàçûâàåòñÿ òðèããåðîì òèïà Å
(exclusive èñêëþ÷èòåëüíûé, îñîáåííûé), àâòîìàò íà ðèñ.7.17 ïîä äåé-
ñòâèåì ñèãíàëà 11 ïåðåõîäèò â ñîñòîÿíèå 0 è íàçûâàåòñÿ òðèããåðîì òèïà
R, à àâòîìàò íà ðèñ. 7.18 ïåðåõîäèò â ñîñòîÿíèå 1 è íàçûâàåòñÿ òðèããå-
ðîì òèïà S. Òàáë.7.8 ïðåäñòàâëÿåò ñîáîé îáùóþ êîäèðîâàííóþ òàáëè-
öó ïåðåõîäîâ ýòèõ òðåõ òðèããåðîâ.
Òàáëèöà 7.8
Ìàòðèöû (7.4), (7.5) è (7.6) ÿâëÿþòñÿ ñîîòâåòñòâåííî ìàòðèöàìè ïå-
ðåõîäîâ òðèããåðîâ E, R è S.
Qt Qt+
12
21
01
10
RS
bb
bb
=
M
(7.4)
01
00
00
01
01
10
10
1111
01
00
01
01
10
10
00
11
11
01
00
00
01
01
10
10
11
11
Ðèñ. 7.16
Ðèñ. 7.17
Ðèñ. 7.18
45
- ðåããèðò- 4 ðåããèðò- 5 ðåããèðò-
010 101
00010 101
01111111
10000000
110 1 0 0 1 1

83
Qt Qt+
12
01
1
0
RS
bb
b
b
=
M
(7.5)
21
0
1
10
RS
b
b
bb
=
M
(7.6)
 ìàòðèöàõ (7.4), (7.5) è (7.6) ýëåìåíòû ìîãóò ïðèíèìàòü ëþáûå çíà-
÷åíèÿ, êðîìå êîìáèíàöèè b
1
= 0 è b
2
= 1 îäíîâðåìåííî, ò. å.
b
1
b
2
= 0.
Àâòîìàò À
4
, ïðåäñòàâëåííûé íà ðèñ. 7.13, ìîæåò áûòü çàêîäèðîâàí
èíà÷å, ñïîñîáîì, ïðåäëîæåííûì â òàáë. 7.9. Òîãäà åãî êîäèðîâàííûé
ãðàô ïåðåõîäîâ áóäåò èìåòü âèä, ïðåäñòàâëåííûé íà ðèñ. 7.19, à òàáëè-
öà ïåðåõîäîâ âèä, ïðåäñòàâëåííûé â òàáë. 7.10.
Òàáëèöà 7.9 Òàáëèöà 7.10
Åñëè ñðàâíèòü òàáëèöó ïåðåõîäîâ ýòîãî àâòîìàòà ñ òàáëèöåé ïåðå-
õîäîâ òðèããåðà òèïà D (òàáë. 7.3), ìîæíî çàìåòèòü, ÷òî ïðè q
(2)
(t) = 1
ñîñòîÿíèÿ àâòîìàòà Q(t+1) â òàáë.7.10 òàê æå, êàê è â òàáë. 7.3, îïðå-
äåëÿþòñÿ òîëüêî çíà÷åíèÿìè âõîäíîãî ñèãíàëà q
(1)
(t). Â òî æå âðåìÿ
ïðè q
(2)
(t) = 0 àâòîìàò ïåðåõîäèò â ðåæèì õðàíåíèÿ èíôîðìàöèè (åãî
ñîñòîÿíèÿ íå ìåíÿþòñÿ) íåçàâèñèìî îò ñìåíû ñèãíàëîâ íà âõîäå q
(1)
(t).
 ñâÿçè ñ ýòèì ðàññìàòðèâàåìûé àâòîìàò ïðåäñòàâëÿåò ñîáîé ìî-
äèôèêàöèþ D-òðèããåðà è íàçûâàåòñÿ òðèããåðîì òèïà DV (valve âåí-
òèëü, êëàïàí), ãäå áóêâàìè D è V îáîçíà÷åíû ñîîòâåòñòâåííî âõîäû q
(1)
è q
(2)
. Âõîä V ÿâëÿåòñÿ ðàçðåøàþùèì âõîäîì ïî îòíîøåíèþ êî âõîäó D.
Ìàòðèöà ïåðåõîäîâ òðèããåðà òèïà DV èìååò âèä
G
G
LG
G
L
L
L
!
L
01
00
00
01
0
1
10
10
11
11
Ðèñ.7.19
