Лукичев Д.В. Моделирование статических характеристик асинхронного двигателя в пакете MATLAB
Подождите немного. Документ загружается.

МЕТОДЫ. АЛГОРИТМЫ. ПРОГРАММЫЙОД
ЙОДМОДЕЛИРОВАНИЕ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК АСИНХРОННОГО ДВИГАТЕЛЯ...
УДК 621.31:004.942
Моделирование статических
характеристик асинхронного
двигателя в пакете MATLAB
Д. В. Лукичев
xxВ статье предлагается достаточно простой и легко воспроизводимый способ построения
полной механической характеристики, а также круговой диаграммы асинхронного двигателя
(АД) в пакете MATLAB/Simulink. В основу методики положено условие статической устой-
чивости АД при работе на нагрузочное устройство. Основными преимуществами подхода
являются:
простота получения характеристик, исключающая необходимость использования допол-
нительных моделей для различных режимов работы двигателя;
значительное сокращение времени на построение и наглядность представления;
возможность анализа процессов в двигателе при его работе на неустойчивом участке
механической характеристики.
Методика позволяет выбрать необходимые параметры модели нагрузки, автоматически стро-
ить механическую характеристику и круговую диаграмму, а также обеспечивает устойчивую
работу двигателя в любой ее точке, что дает возможность анализировать процессы в АД
во всем диапазоне скоростей. Также при дополнении соответствующими блоками возможно
построение всех рабочих характеристик машины.
1. Введение
MATLAB совместно с Simulink и Power System Block-
set позволяют исследовать процессы и параметры элек-
трических машин, которые зачастую недоступны в ре-
альных объектах. В библиотеках этих пакетов имеются
многочисленные виртуальные элементы и измеритель-
ные приборы, позволяющие исследовать электрическую
цепь любой сложности. Но не всегда использование од-
них лишь стандартных блоков оказывается достаточным
для оптимального решения какой-либо специфической
задачи.
Основной трудностью при получении механической
характеристики асинхронного двигателя в различных
прикладных пакетах является его опрокидывание при
выходе на неустойчивые участки. В [1] механическую
характеристику асинхронного двигателя предлагается
строить по точкам, последовательно задавая момент на-
грузки и сохраняя полученную при этом скорость враще-
ния. При такой методике точки механической характе-
ристики могут быть получены только на участке устой-
чивой работы, а снятие режима короткого замыкания
требует дополнительного изменения в модели. Помимо
этого, к недостаткам данного подхода можно отнести,
во-первых, его трудоемкость, поскольку качество полу-
ченной характеристики напрямую зависит от количества
точек, а во-вторых, полное отсутствие информации о по-
ведении асинхронной машины на неустойчивом участке
работы.
Для понимания работы асинхронных машин необхо-
димо знать, как будут изменяться токи, потери, КПД
и cos ϕ при вариации нагрузки на валу. Эти показатели
при изменении скольжения s от −∞ до +∞ с достаточ-
ной точностью позволяет определить круговая диаграм-
ма, которая имеет важное значение в теории и до сих пор
используется для построения рабочих характеристик.
АВТОР
Лукичев Дмитрий
Вячеславович
Аспирант кафедры
электротехники и прецизионных
электромеханических систем;
Государственный университет
информационных технологий,
механики и оптики,
г. Санкт-Петербург
86
#3—4 (7—8) 2004
Д. В. ЛУКИЧЕВЙОД
ЙОДМЕТОДЫ. АЛГОРИТМЫ. ПРОГРАММЫ
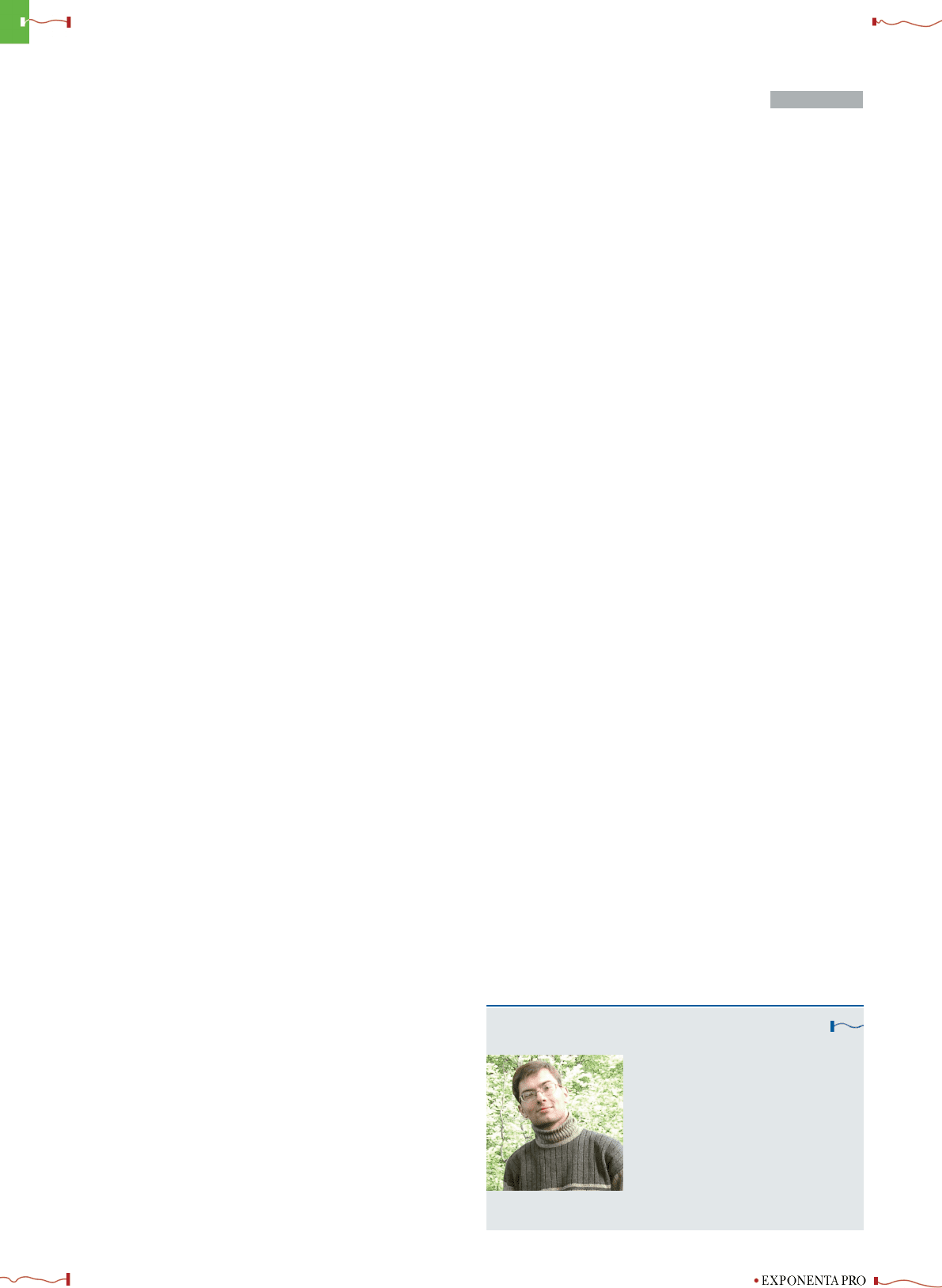
Рассмотрим, в чем же состоит особенность кривой ме-
ханической характеристики асинхронного двигателя и
как обеспечить возможность автоматического построе-
ния непрерывной, полной механической характеристи-
ки асинхронного двигателя (МХ АД) и его круговой
диаграммы.
Рис. 1. Механические характеристики АД и некоторых производ-
ственных механизмов.
2. Механическая характеристика и
устойчивость работы асинхронного
двигателя
Уравнение динамики электромеханической системы
имеет следующий вид [2]:
M − M
c
= J
dΩ
dt
,
(2.1)
где M , J, Ω=Ω
c
, M
c
— соответственно, электромагнит-
ный момент, развиваемый машиной, ее момент инерции
и частота вращения, а также момент сопротивления на
ее валу.
Из (2.1) следует, что для устойчивой работы двигате-
ля, приводящего в действие какой-либо производствен-
ный механизм, необходимо определенное сочетание па-
раметров механических характеристик двигателя M(Ω)
и нагрузки M
c
(Ω). Двигатель работает устойчиво, когда
жесткость его механической характеристики в точке ста-
тического равновесия (при M = M
c
) меньше жесткости
нагрузки:
dM
dΩ
<
dM
c
dΩ
.
(2.2)
Чаще всего для анализа работы двигателя в различ-
ных программных пакетах используется статическая на-
грузка (прямая 2 на рис. 1), которая задается либо скач-
ком (Step), либо постоянным значением (Constant). То-
гда механическая характеристика АД (кривая 1) может
быть условно разделена на три участка: участок стати-
ческой устойчивости AB и два участка неустойчивой ра-
боты двигателя — ADD
и BCC
.
Если машину нагрузить статическим положительным
(отрицательным) моментом, то при его значениях, боль-
ше максимального электромагнитного момента в дви-
гательном (генераторном) режиме, появляется неком-
а)
б)
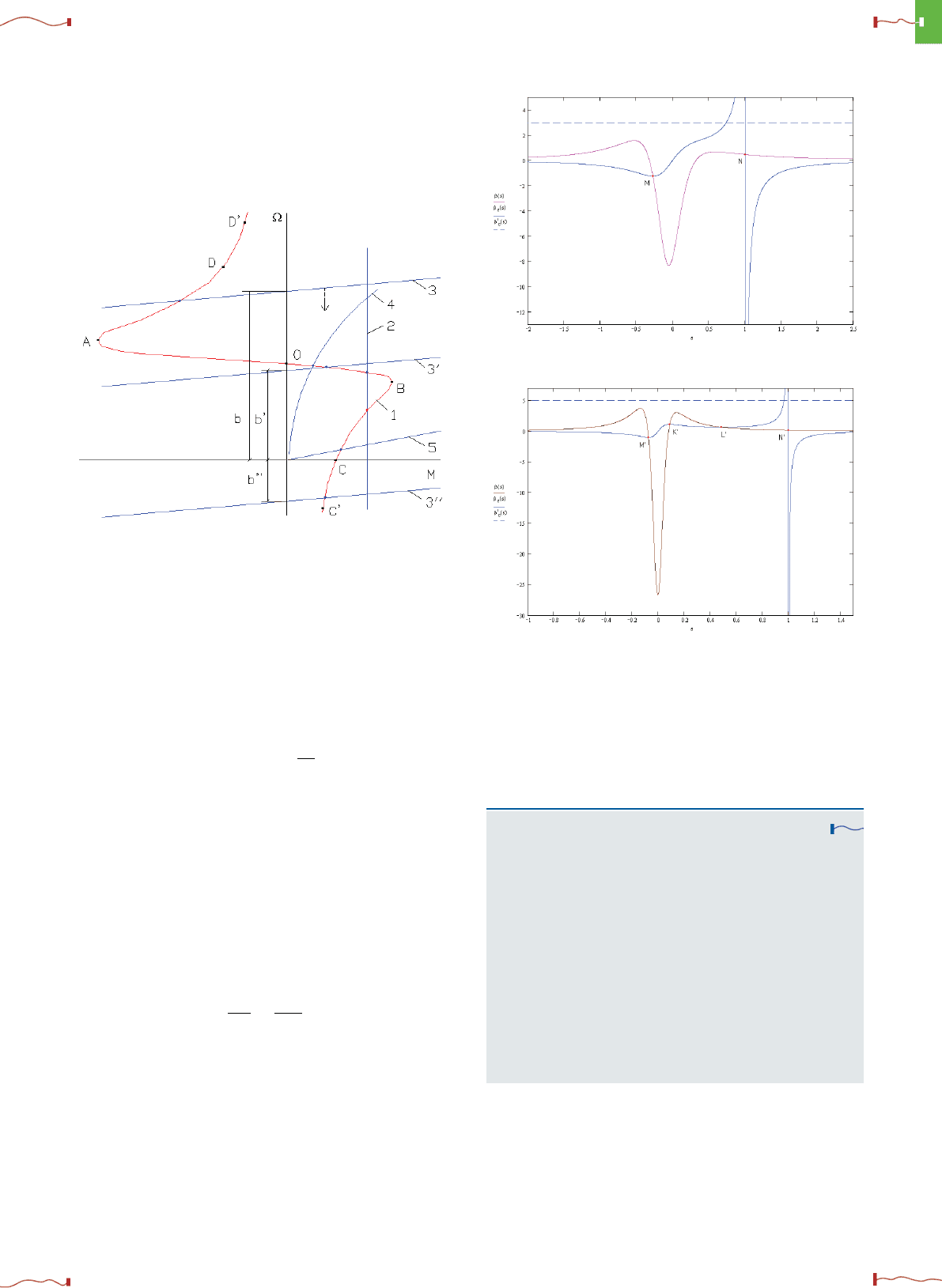
Рис. 2. Графики жесткости МХ АД при различных параметрах дви-
гателя: а) АД1: s
k
=0.323, c =0.243;б)АД2:s
k
=0.08, c =0.06.
пенсируемый ускоряющий момент (M − M
c
), и частота
вращения начинает стремительно падать по кривой ме-
ханической характеристики 1. В таком случае говорят
об опрокидывании двигателя, и получение статически
устойчивых точек является невозможным.
РЕЗЮМЕ
Задача
Моделирование статических характеристик асинхрон-
ного двигателя.
Программные средства
Power System Blockset for MATLAB 5.3.
Результаты
Предложен способ автоматического построения пол-
ной механической характеристики и круговой диа-
граммы асинхронного двигателя.
Известно, что полная статическая устойчивость на-
блюдается при работе АД на вентиляторную нагруз-
ку (кривая 4), которая обеспечивает выполнение усло-
вия (2.2) в двигательном режиме. Однако в других ре-
жимах для получения устойчивой работы такую нагру-
зочную характеристику необходимо видоизменять, при-
чем это изменение напрямую зависит от того, в каком
из режимов работает машина, что, несомненно, являет-
МАТЕМАТИКА В ПРИЛОЖЕНИЯХ
87
МЕТОДЫ. АЛГОРИТМЫ. ПРОГРАММЫЙОД
ЙОДМОДЕЛИРОВАНИЕ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК АСИНХРОННОГО ДВИГАТЕЛЯ...
а)
б)
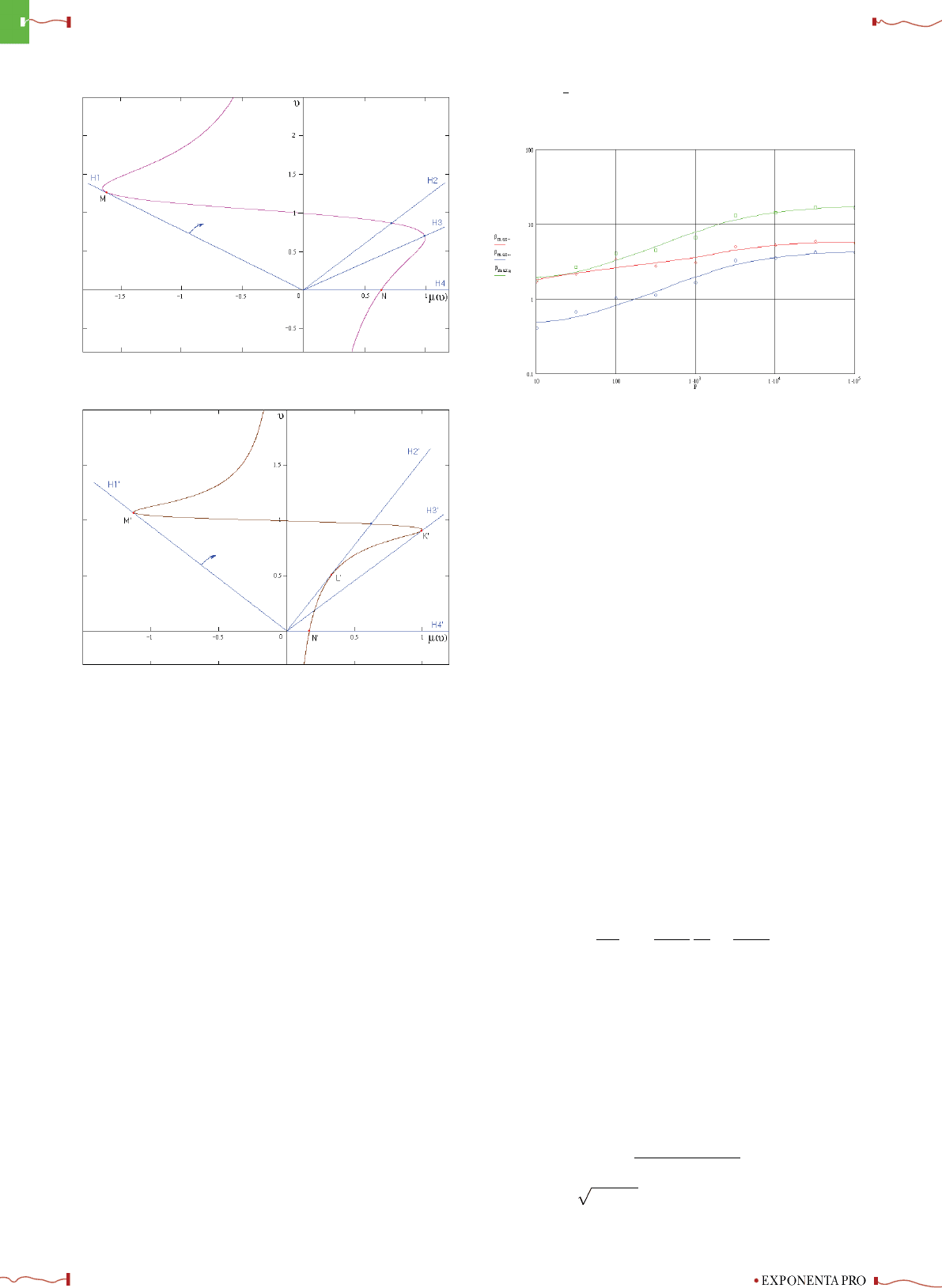
Рис. 3. Графики МХ АД при различных параметрах двигателя:
а) АД1: s
k
=0.323, c =0.243;б)АД2:s
k
=0.08, c =0.06.
ся весьма трудоемкой задачей, требующей составления
сложных алгоритмов. Нетрудно заметить, что для на-
грузочного механизма, характеризуемого линейной за-
висимостью вида 3 (рис. 1), условие статической устой-
чивости выполняется в каждой точке, поэтому на всех
участках механической характеристики двигатель будет
работать устойчиво. Выражение для механической ха-
рактеристики нагрузки такого типа в общем виде запи-
шется как
Ω
c
= aM
c
+ b,
где a, b — угол наклона и смещение характеристики от-
носительно оси момента, откуда получим уравнение для
момента нагрузки, имеющего линейную характеристику
в точке статического равновесия
M
c
= α(Ω − b), (2.3)
где α =1/a — жесткость механической характеристики.
Таким образом, вариация значений коэффициентов a
и b, обеспечивающих выполнение условия (2.2), позволя-
ет нам получать статически устойчивую работу двига-
теля во всем диапазоне скоростей. Наиболее просто это
достигается:
изменением жесткости α =1/a нагрузки при неиз-
менном b;
изменением величины смещения b при постоянной
жесткости α.
При достаточно большом диапазоне изменения сколь-
жений можно определить также координаты вектора то-
ка статора i
1
в статическом режиме и, представив их в
графической форме, получить круговую диаграмму ма-
шины.
Рис. 4. Зависимость жесткости МХ от мощности двигателей се-
рии 4А.
3. Метод, основанный на изменении
жесткости нагрузки
Если представить момент нагрузки линейной функци-
ей, проходящей через начало координат (b =0: линия 5),
то из (2.3) получим следующее уравнение:
M
c
= αΩ. (3.1)
Изменяя жесткость α, мы тем самым будем менять
угол наклона характеристики нагрузки к оси момен-
та, что позволит получать различные точки статическо-
го равновесия на МХ АД. Однако для проверки вы-
полнения условия (2.2) при таком характере нагруз-
ки необходимо определить характер изменения жестко-
сти МХ АД.
Выразим частоту вращения через скольжение s,ис-
пользуя известное выражение
Ω=Ω
1
(1 − s), (3.2)
где Ω
1
— частота вращения двигателя в точке холостого
хода. Тогда выражение для жесткости преобразуется к
виду:
α =
dM
dΩ
= −
M
max
Ω
1
dµ
ds
=
M
max
Ω
1
β,
где µ = M/M
max
— относительный электромагнитный
момент, β = −dµ/ds — жесткость МХ в функции сколь-
жения. Следовательно, условие (2.2) устойчивой работы
АД можно записать как
β<β
c
. (3.3)
Для нахождения экстремумов жесткости МХ АД вос-
пользуемся формулой М. Клосса [3]:
µ =
2(1 + c)
2/s
k
+ s
k
/s +2c
,
(3.4)
где s
k
= ±r
2
/ r
2
1
+ x
2
k
— критическое скольжение, а ве-
личина c определена равенством c = s
k
r
1
/r
2
.
Производная выражения (3.4) представляет собой
88
#3—4 (7—8) 2004
Д. В. ЛУКИЧЕВЙОД
ЙОДМЕТОДЫ. АЛГОРИТМЫ. ПРОГРАММЫ
Рис. 5. Модель системы для исследования асинхронного двигателя.
жесткость МХ АД
dµ
ds
=2s
k
(s
2
k
− s
2
)
1+c
(s
2
+ s
2
k
+2cs
k
s)
2
. (3.5)
Поскольку рассматриваемая нагрузочная характери-
стика проходит через начало координат, то для нахожде-
ния ее жесткости достаточно значение момента в точке
статического равновесия поделить на соответствующее
ему значение частоты вращения. Воспользовавшись вы-
ражениями (3.2) и (3.4), получим с учетом знака
dµ
c
ds
=
2(1 + c)
(s/s
k
+ s
k
/s +2c)(s − 1)
.
На рис. 2 приведены графики жесткости МХ двигате-
ля (кривая β(s)) и нагрузки (кривая β
c
(s)) при различ-
ных параметрах АД.
Из рисунков следует, что для рассматриваемой на-
грузки условие статической устойчивости (3.3) не выпол-
няется в области отрицательных скольжений приблизи-
тельно при s<−s
k
, а также при s ≥ 1, где в точке ко-
роткого замыкания жесткость МХ нагрузки имеет раз-
рыв. В этой точке вообще невозможно создать нагруз-
ку, поскольку при этом ее МХ должна иметь бесконечно
большую жесткость. На рис. 3 приводятся механические
характеристики двигателей АД1 и АД2, а также МХ на-
грузки вида (3.1) при различных α.
4. Метод, основанный на изменении
коэффициента смещения нагрузки
Обратимся теперь ко второму из предложенных спо-
собов. Если в выражении (2.3) параметр нагрузки α сде-
лать достаточно большим (см., например, прямую β
c
(s)
на рис. 2), то условие статической устойчивости будет
обеспечиваться во всем диапазоне скоростей.
Уменьшение смещения характеристики нагрузки b
при неизменной жесткости с начальной положительной
величины в зону отрицательных значений показано на
рис. 1 (характеристики 3, 3
и 3
соответственно), что
позволяет нам получать точки статического равновесия
на кривой МХ АД.
Однако для выбора коэффициента жесткости нагру-
зочной характеристики существует ограничение, связан-
ное с положительной жесткостью характеристики АД на
участках ADD
и BCC
. Для выполнения условия стати-
ческой устойчивости необходимо выбрать параметр на-
грузки больше максимальной жесткости характеристики
АД на этих участках.
Для этого найдем вторую производную выраже-
ния (3.4) и определим экстремумы функции жесткости:
d
2
µ
ds
2
=
4(1 + c)
(s/s
k
+ s
k
/s +2c)
3
1
s
k
−
s
k
s
2
2
−
−
4(1 + c)
(s/s
k
+ s
k
/s +2c)
2
s
k
s
3
=0.
Максимумы характеристики соответствуют скольжению
s
m
= s
k
c + c
2
− 1
1/3
+ c + c
2
− 1
−1/3
.
При условии, что c ≤ 1, модуль комплексного числа
под корнем третьей степени равен единице. Следователь-
но, сумма чисел в выражении для s
m
вещественна, по-
скольку обратное число является комплексно сопряжен-
ным. Таким образом, выражение в скобках равно удво-
енному значению вещественных составляющих
s
m
=2s
k
cos
1
3
arctan
√
1 − c
2
c
= s
k
s
mm
.
Подставив получившееся значение скольжения в урав-
нение (3.5), найдем выражение для максимальной жест-
МАТЕМАТИКА В ПРИЛОЖЕНИЯХ
89
МЕТОДЫ. АЛГОРИТМЫ. ПРОГРАММЫЙОД
ЙОДМОДЕЛИРОВАНИЕ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК АСИНХРОННОГО ДВИГАТЕЛЯ...
Рис. 7. Блок построения круговой диаграммы АД.
Рис. 6. Блок построения механической характеристики.
кости кривой механической характеристики АД:
β
max
=
2(1 + c)(s
2
mm
− 1)
(s
2
mm
± 2cs
mm
+1)
2
s
k
. (4.1)
При отрицательных скольжениях жесткость МХ АД
больше и равна
β
max−
=
2(1 + c)(s
2
mm
− 1)
(s
2
mm
− 2cs
mm
+1)
2
s
k
, (4.2)
поэтому параметры МХ нагрузки необходимо выбирать
из условия
α
min
>
|M
max−
|
Ω
1
β
max−
,
где M
max−
— максимальный момент в генераторном ре-
жиме АД.
У машин большой мощности критическое скольжение
мало, поэтому значением c можно пренебречь. Тогда при
c → 0 получаем s
mm
=
√
3, и выражение (4.1) преобра-
зуется к виду
β
max−
=
1
4s
k
. (4.3)
На рис. 4 приводятся графики жесткости МХ, рассчи-
танные по формулам (4.2), (4.3) для серии двигателей 4А
вдиапазонемощностейот60Втдо90кВт[4].
Приближенные значения жесткости β
max−
значитель-
но меньше, чем точные, но в то же время крутизна кри-
вой β
max∼
(P ) больше, чем β
max−
(P ). Поэтому в выра-
жение (4.3) можно ввести поправочный коэффициент,
обеспечивающий β
max∼
>β
max−
при минимальной мощ-
ности. Тогда для больших мощностей это условие бу-
дет выполняться всегда. Таким образом, выражение для
жесткости β
max
примет вид:
β
max≈
=
k
4s
k
. (4.4)
Простейшим коэффициентом в выражении (4.4) для се-
рии двигателей 4А является число 4 (см. рис. 4), при
этом минимально допустимая жесткость характеристи-
ки нагрузки α определяется выражением:
α
min
>
|M
max−
|
Ω
1
s
k
. (4.5)
Рис. 8. Изменение модуля и угла обобщенного вектора токастатора.
90
#3—4 (7—8) 2004

Д. В. ЛУКИЧЕВЙОД
ЙОДМЕТОДЫ. АЛГОРИТМЫ. ПРОГРАММЫ
Однако следует учесть, что при моделировании МХ
возможна динамическая ошибка, связанная с тем, что
нагрузочный момент АД изменяется во времени с неко-
торой скоростью. Оценим эту ошибку, пользуясь уравне-
нием движения (2.1). Для линеаризации уравнения пред-
ставим все величины через установившиеся значения и
приращения в виде:
M = M
0
+ α∆Ω,
M
c
= M
0
+ α
c
∆Ω,
Ω=Ω
0
+∆Ω=Ct +∆Ω,
где ∆Ω и C — соответственно приращение и скорость
изменения частоты вращения. Тогда
dΩ
dt
= C +
d∆Ω
dt
.
Подставляя эти выражения в (2.1), получим:
d∆Ω
dt
+
α
c
− α
J
∆Ω = −C.
(4.6)
Корень характеристического уравнения и постоянная
времени равны соответственно
p = −
α
c
− α
J
,
τ =
J
α
c
− α
.
Общее решение уравнения (4.6) запишется как
∆Ω = −τC(1 − e
pt
).
Установившееся значение приращения частоты враще-
ния представляет собой динамическую ошибку ε, кото-
рая по окончании переходных процессов составит вели-
чину −τC. В знаменателе выражения для τ присутству-
ет постоянная жесткость МХ нагрузки α
c
, выбранная
из условия (4.5), и переменная жесткость МХ АД, да-
ваемая выражением α = F(s). Очевидно, что максимум
динамической ошибки при заданной скорости изменения
частоты вращения C будет соответствовать максималь-
ному значению постоянной времени
τ
max
=
J
α
c
−|M
max−
|β
max−
/Ω
1
,
т. е. будет соответствовать экстремуму жесткости в гене-
раторном режиме. Соответственно, абсолютное значение
динамической ошибки при этом будет равно:
ε
add
= τ
max
C. (4.7)
Отсюда делаем выводы.
1. Надлежащим выбором скорости изменения часто-
ты вращения C всегда можно обеспечить условие ε
max
<
ε
add
, т. е. снизить динамическую ошибку до любого на-
перед заданного допустимого значения ε
add
.Так,для
АД серии 4А при скорости изменения частоты враще-
ния C = 100 и жесткости МХ нагрузки, выбранной из
условия (4.5), динамическая ошибка составляет величи-
ну порядка 0, 2÷1%.
2. Поскольку уменьшение скорости изменения часто-
ты вращения значительно замедляет моделирование,
для снижения динамической ошибки целесообразно уве-
личивать жесткость МХ нагрузки α
c
.
5. Реализация предлагаемого
метода
Обобщенная виртуальная установка для исследования
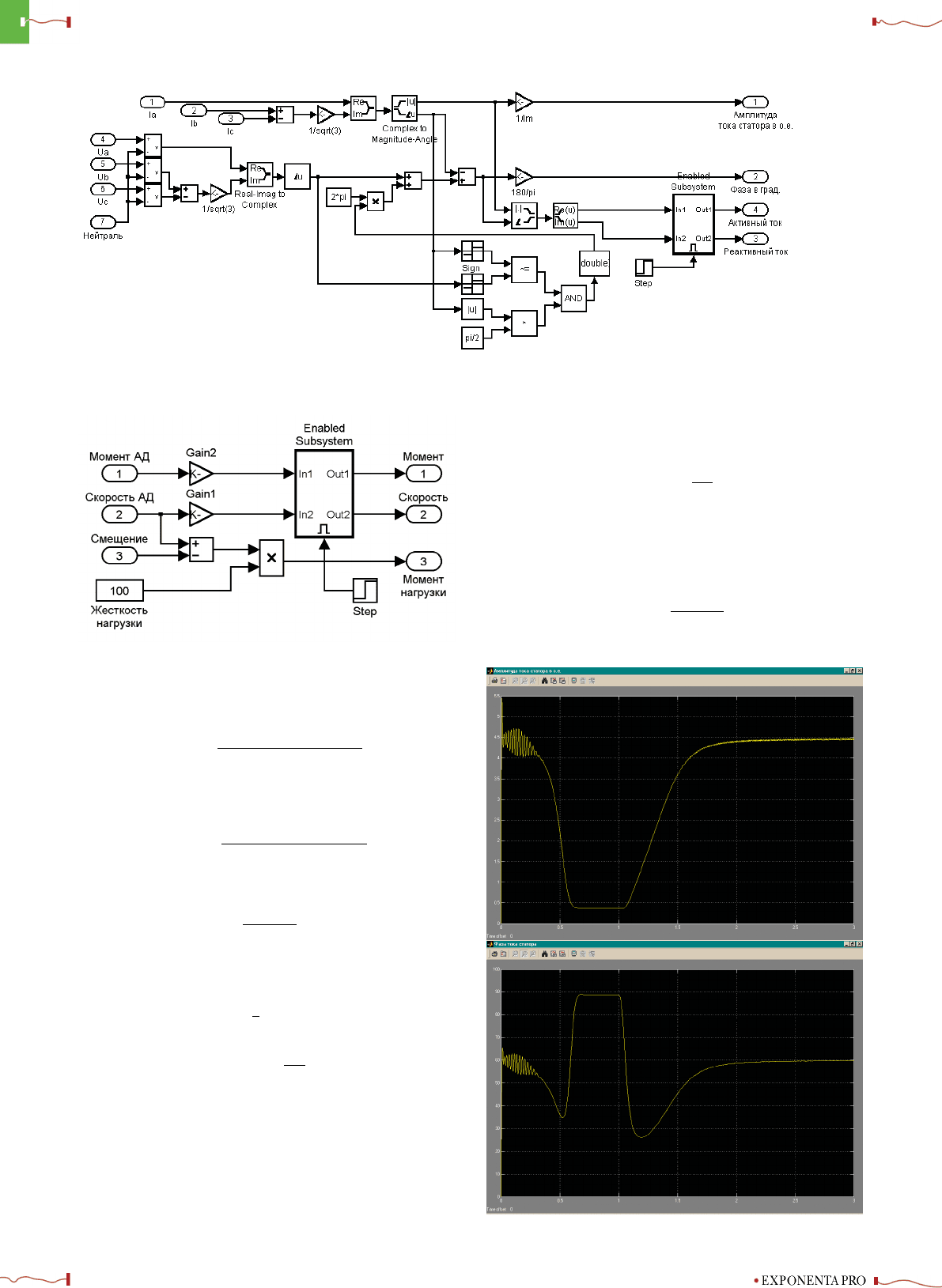
асинхронной машины представлена на рис. 5. Модель
содержит:
источник переменного трехфазного напряжения (3-
ph. Sourse);
исследуемую трехфазную асинхронную машину
(Asynchronous Machine);
универсальный блок измерений (Machines Measure-
ment Demux) для вывода переменных состояний ма-
шины;
блок построения механической характеристики
(Mech. Char.);
блок линейного нарастания коэффициента смеще-
ния нагрузки (Ramp);
блок насыщения (Saturation);
блок построения круговой диаграммы АД (Circ.
Diagram);
различные графопостроители и блоки измерений.
Блок Mech. Char., реализующий алгоритм (2.3), имеет
структуру, приведенную на рис. 6. Жесткость характе-
ристики нагрузки выбирается из выражения (4.5). Для
построения МХ, начиная со второго квадранта, в первый
момент времени на вход «Смещение» подается началь-
ное положительное значение коэффициента b из блока
Ramp. Для получения режима электромагнитного тор-
моза при отрицательных значениях момента смещение
выбирается из условия
b>2Ω
1
.
Построение МХ начинается в момент времени t
m
по-
сле завершения разгона АД с отрицательным моментом
нагрузки. При этом в блоке Ramp начинается линейное
уменьшение величины смещения со скоростью C,вы-
бранной с учетом выражения (4.7). Значение t
m
выби-
рается из условия окончания электромеханических пе-
реходных процессов t
m
≥ 3T
m
,гдеT
m
— механическая
постоянная, полученная с учетом параметров нагрузки
АД. С помощью блока Step, имеющего в момент време-
ни t
m
скачок из нуля в единицу и управляющего работой
блока Enabled Subsystem, выходные сигналы «Момент»
и «Скорость» до момента времени t
m
на графопостро-
итель не подаются. Блоки Gain1 (коэффициент усиле-
ния 1/Ω
1
) и Gain2 (с коэффициентом 1/M
nom
) позволяют
привести сигналы скорости и момента к относительным
величинам.
На рис. 7 приводится структура блока построения кру-
говой диаграммы АД.
Фазовый угол и величину измеряемого тока и напря-
жения можно определять с помощью блока Fourier из
библиотеки Power System Blockset, как это делается в [1].
Такой подход имеет ряд неудобств. Во-первых, для точ-
ного вычисления этих параметров требуется выборка
определенной длины, а во-вторых, при моделировании
системы «источник питания — АД» выходные сигналы
блока Fourier имеют пульсации, которые уменьшаются с
уменьшением временного шага, что в свою очередь ощу-
тимо замедляет моделирование. Чтобы избежать этого,
воспользуемся понятием обобщенного вектора.
В блоке Circ. Diagram в каждый момент времени по
известным токам в фазах статора АД определяется обоб-
МАТЕМАТИКА В ПРИЛОЖЕНИЯХ
91
МЕТОДЫ. АЛГОРИТМЫ. ПРОГРАММЫЙОД
ЙОДМОДЕЛИРОВАНИЕ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК АСИНХРОННОГО ДВИГАТЕЛЯ...
а)
б)
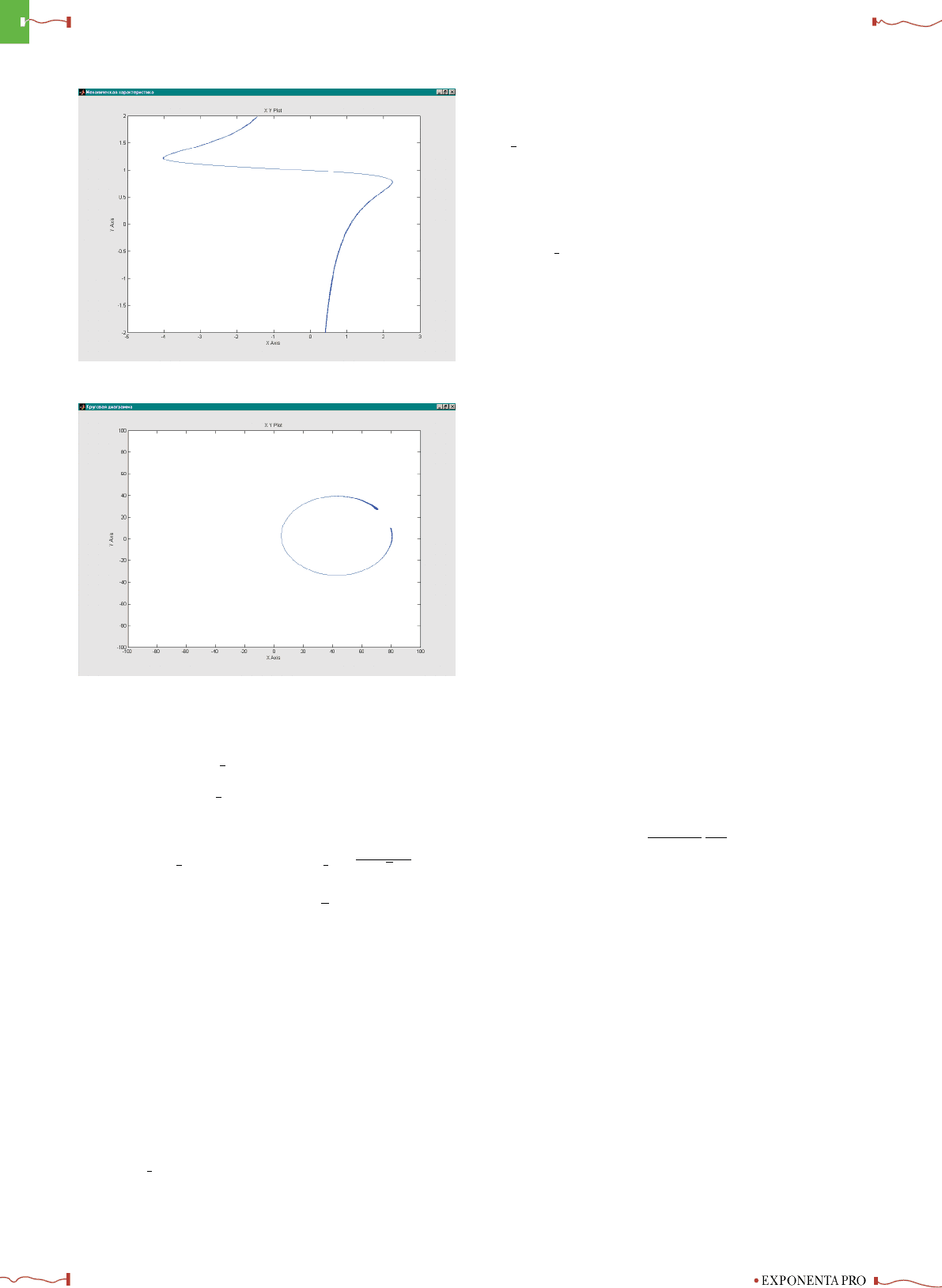
Рис. 9. а) механическая характеристика асинхронного двигателя;
б) круговая диаграмма асинхронного двигателя.
щенный вектор тока i
1
:
i
1
= i
1 α
+ ji
1 β
,
где
i
1 α
=Rei
1
= i
1 a
,i
1 β
=Imi
1
=
i
1 b
− i
1 c
√
3
.
Обобщенный вектор напряжения u
1
находится анало-
гичным образом. Далее с помощью стандартных блоков
Real-Imag to Complex и Complex to Magnitude-Angle вы-
числяется модуль и фазовый угол данных векторов от-
носительно момента начала моделирования. Для постро-
ения круговой диаграммы требуется определить угол ϕ
между ними. Но поскольку в блоках Simulink угол при-
нимает значения только от −π до +π, то для полу-
чения правильного результата (разности) необходимо
продлевать линейную характеристику угла напряжения
(уменьшаемое), пока угол тока (вычитаемое) не достиг-
нет своего максимального значения +π и не изменится
на противоположный.
При изменении момента нагрузки (а следовательно, и
скольжения АД) меняется как значение угла ϕ,таки
значение |i
1
|. Таким образом, точки круговой диаграм-
мы можно получить, откладывая по оси ординат актив-
ную составляющую обобщенного вектора тока статора, а
по оси абсцисс — соответственно его реактивную состав-
ляющую. Получение этих составляющих достигается об-
ратным преобразованием Magnitude-Angle to Complex —
Complex to Real-Imag.
На рис. 8 приводятся графики изменения модуля то-
ка |i
1
| в относительных единицах и угла ϕ в [град] при
разгоне АД до режима холостого хода (начальное смеще-
ние в блоке Rate задаем равным Ω
1
) и далее при увели-
чении момента нагрузки и уменьшении частоты враще-
ния до нулевого значения. Из графиков наглядно видно,
что в режиме холостого хода угол ϕ стремится к 90
o
,а
значение |i
1
| уменьшается до тока холостого хода.
Блок также позволяет продемонстрировать изменение
соотношения активной и реактивной составляющих тока
статора в процессе работы АД.
Графики полной механической характеристики АД, а
также круговой диаграммы, получающиеся при модели-
ровании, приведены на рис. 9.
Чтобы исследовать поведение двигателя в какой-либо
точке механической характеристики, достаточно в канал
изменения смещения нагрузочной характеристики вклю-
чить блок насыщения Saturation (см. рис. 1), который
при достижении нужной величины зафиксирует ее, тем
самым установив соответствующий данному значению
постоянный момент нагрузки. Каждая точка МХ харак-
теризуется двумя параметрами — частотой вращения и
моментом. Таким образом, задаваясь одним из этих па-
раметров, второй можно всегда определить из форму-
лы Клосса (3.4) и далее, воспользовавшись уравнени-
ем (2.3), найти искомое значение смещения b. Двигатель
будет устойчиво работать в этой точке, что позволит про-
анализировать его характеристики.
6. Заключение
Предложенный метод моделирования статических ха-
рактеристик АД позволяет выбрать параметры нагруз-
ки таким образом, чтобы автоматически построить пол-
ную механическую характеристику и круговую диаграм-
му двигателя. Жесткость модели нагрузки рекомендует-
ся рассчитывать из соотношения
α>
|M
max−
|
Ω
1
k
4s
k
,
где k =4для машин серии 4А, а скорость изменения
смещения — задавать из уравнения C = ε
add
/τ
max
.Дан-
ный подход дает возможность исследовать работу АД
в любой точке механической характеристики, а также
(при дополнении соответствующими блоками) получить
все рабочие характеристики машины.
Литература
1. Герман-Галкин С. Г., Кардонов Г. А. Электрические ма-
шины: Лабораторные работы на ПК.— СПб.: КОРОНА
принт, 2003.— 256 с.
2. Чиликин М. Г., Ключев В. И., Сандлер А. С. Тео-
рия автоматизированного электропривода.— М.: Энер-
гия, 1979.— 616 с.
3. Костенко М. П., Пиотровский Л. М. Электрические ма-
шины. В 2-х ч. Ч. 2. Машины переменного тока.— М.:
Госэнергоиздат, 1958.— 651 с.
4. Копылов И. П. Математическое моделирование электри-
ческих машин.— М.: Высшая школа, 1994.— 318 с.
92
#3—4 (7—8) 2004
