Ложкин С.А. Лекции по основам кибернетики
Подождите немного. Документ загружается.


§4. Операция суперпозиции. Разделительные КС 41
• •
•
•
''ww
•
•
x
1
x
2
z
1
&
∨
¬
&
Σ
2
•
•
/
/
/
-
-
-
Σ
2
•
2
2
2
2
Σ
2
,
,
,
,
. . .
•
x
1
x
2
x
3
x
q
z
1
a) b)
Рис. 4.2: пример суперпозиции СФЭ
в присоединениях и совпадающему с выходом ФЭ,
присоединяется в точности один бесповторный вход Σ
00
.
Рассмотрим теперь во просы, связанные с нахождением
функционирования для суперпозиций сетей или КС.
Из соображений удобства будем допускать наличие
в КС ориентированных (неориентированных) ребер
без пометок, которые проводят при любых значениях
управляющих входных БП и называются вентилями
(соответственно проводниками). Это позволяет считать,
что сети являются частным случаем КС и реализуют свои
матрицы достижимости, состоящие из константных ФАЛ.
Операция суперпозиции КС и все ее частные случаи
определяются обычным образом. При этом пометками
входов и выходов КС, в отличие от СФЭ, не обязательно
являются переменные, а БП, управляющие проводимостью
контактов КС, никак не связаны с ее входами.

42 Глава 2. Основные классы управл яющих систем
Легко видеть, что перестановка входов(выходов)
КС порождает в реализуемой ею матрице такую же
перестановку связанных с ними строк (соответственно
столбцов), а снятие (дублирование) выходов этой КС —
удаление (соответственно добавление) связаных с ними
столбцов. Заметим также, что КС Σ, которая является
объединением КС Σ
0
и Σ
00
, реализующих матрицы F
0
и F
00
соответственно, реализует матрицу F вида
1
:
F =
F
0
0
0 F
00
Обратимся, далее, к особенностям функционирования
КС, получающихся в результате применения операций
суперпозиции общего вида. Заметим также, что
суперпозиция общего вида Σ = Σ
00
(Σ
0
) всегда может
быть сведена к стыковке вида Σ =
b
Σ
00
(
b
Σ
0
), где схемы
b
Σ
0
и
b
Σ
00
получаются из схем Σ
0
и Σ
00
соответственно добавлением
тождественных вершин и переименованием выходов.
Стыковка вида Σ = Σ
00
(Σ
0
), в свою очередь, может быть
сведена к бесповторной стыковке вида Σ =
b
Σ
00
(
b
Σ
0
), где
схемы
b
Σ
0
и
b
Σ
00
получаются из схем Σ
0
и Σ
00
снятием выходов
и отождествлением входов соответственно.
Легко видеть, что результат отождествления первых p
входов КС Σ эквивалентен результату стыковки вида Σ (Σ
0
),
а результат p-кратного дублирования первого выхода КС
Σ — результату стыковки Σ
00
(Σ), где КС Σ
0
, Σ
00
состоят
из (1, p)-проводящей звезды (см. рис. 4.3a, a — вход) и
тождественных вершин. Заметим также, что стыковка вида
Σ(
b
Σ), где КС
b
Σ состоит из (p, 1)-проводящей звезды (см. рис.
1
Предполагается, что номер любого входа (выхода) КС Σ
0
меньше
номера любого входа (соответственно выхода) КС Σ
00
в КС Σ, а
внутренняя упорядоченность полюсов КС Σ
0
и Σ
00
в КС Σ сохраняется.
В остальных случаях происходит необходимая перестановка входов и
выходов КС Σ.

§4. Операция суперпозиции. Разделительные КС 43
?
?
?
?
?
?
?
?
?
?
?
a
a
1
a
2
a
p
. . .
. . .
. . .
?
?
?
?
?
?
?
?
?
?
?
'
'
'
'
'
'
'
'
a
a
1
a
2
a
p
. . .
a) b)
. . .
?
?
?
?
?
?
?
?
?
?
?
'
'
'
'
'
'
'
'
z
1
y
1
y
2
y
p
c)
Рис. 4.3: проводящие и вентильная звезды порядка p
4.3b, a — выход) и тождественных вершин, соответствует
отождествлению первых p выходов КС Σ.
Схема называется разделительной по входам(выходам),
если ФАЛ проводимости между любыми ее различными
входами (соот ветствен но выходами) равна 0. Так (p, 1)-
схема Σ
00
= Σ
00
(y
1
, . . . , y
p
; z
1
), показанная на рисунке
4.3c, является разделительной по входам схемой, которая
называется вентильной зв ездой порядка p. Примером
разделительной по выходам (входам) КС может служить
(1, 2
n
)- (соответственно (2
n
, 1)-) контактное дерево порядка
n (см. рис. 5.4). Будем говорить, что КС Σ от БП x
1
, . . . , x
n
разделительна на наборе α = (α
1
, . . . , α
n
) значений этих
БП, если соответствующей разделительностью обладает
сеть Σ|
α
. Следующее утверждение является обобщением

44 Глава 2. Основные классы управл яющих систем
известной леммы Шеннона (см. [32, 14]).
Лемма 4.1. Пусть КС Σ является результатом
стыковки вида Σ = Σ
00
(Σ
0
), а F , F
0
и F
00
— матрицы,
реализуемые КС Σ, Σ
0
и Σ
00
соответственно. Тогда
F > F
0
· F
00
и F = F
0
· F
00
, (4.1)
если КС Σ
00
разделительна по входам или КС Σ
0
разделительна по выходам.
Доказательство. Пусть КС Σ является сначала
результатом бесповторной стыковки (p, q)-КС Σ
0
и (q, s)-
КС Σ
00
от БП x
1
, . . . , x
n
. Пусть, кроме того, v
0
(v
00
) —
произвольная вершина КС Σ
0
(соответственно Σ
00
), а ФАЛ
f
0
j
(соответственно f
00
j
), j ∈ [1, q], — ФАЛ проводимости от
вершины v
0
к j-му выходу в КС Σ
0
(соответственно от j-го
входа к вершине v
00
в КС Σ
00
). Докажем, что для ФАЛ f —
ФАЛ проводимости от вершины v
0
к вершине v
00
в КС Σ, –
справедливо неравенство
f (x
1
, . . . , x
n
) > f
0
1
· f
00
1
∨ ··· ∨ f
0
q
· f
00
q
, (4.2)
которое переходит в равенство
f (x
1
, . . . , x
n
) = f
0
1
· f
00
1
∨ ··· ∨ f
0
q
· f
00
q
, (4.3)
если КС Σ
0
разделительна по выходам или КС Σ
00
разделительна по входам.
Действительно, пусть a
j
, j ∈ [1, q], — вершина КС
Σ, которая получается в результате присоединения j-го
входа КС Σ
00
к j-му выходу КС Σ
0
(см. рис. ??122a).
Справедливость неравенства ((4.2)) следует из того, что
его правая часть описывает «суммарную» проводимость
тех (v
0
− v
00
)-цепей КС Σ, которые проходят ч ерез вер шины
a
1
, . . . , a
q
ровно один раз (см. рис. 4.4a). Любая другая

§4. Операция суперпозиции. Разделительные КС 45
Σ
0
•
a
0
p
•
a
0
1
. . .
•
a
00
s
•
a
00
1
. . .
•
•
•
•
v
0
•
v
00
a
1
a
j
a
q
Σ
00
a)
Σ
0
•
a
0
p
•
a
0
1
. . .
•
a
00
s
•
a
00
1
. . .
•
•
a
1
a
q
•
a
j
1
•
a
j
2
•
a
j
t
. . .
•
v
0
•
v
00
b)
Рис. 4.4: к доказательству леммы 4.1

46 Глава 2. Основные классы управл яющих систем
(v
0
− v
00
)-цепь КС Σ пр оходит через указанные вершины не
меньше трех раз (см. рис. 4.4b) и в случае разделительности
КС Σ
0
по выходам или разделительности КС Σ
00
по входам
имеет нулевую проводимость.
Из (4. 2) и (4.3) непосредственно вытекает (4.1) с учетом
того, что при v
0
= a
0
i
и v
00
= a
00
j
, где i ∈ [1, p] и j ∈
[1, s], левая(правая) часть этих соотношений равна элементу
матрицы F (соответственно F
0
· F
00
), расположенному в i-й
строке и j-м столбце.
Пусть теперь КС Σ по лучается из КС Σ
00
в результате
применения операции отождествления входов, то есть Σ
эквивалентна бесповторно й стыковке вида Σ
00
(Σ
0
), где КС
Σ
0
состоит из проводящей звезды и тождественных вершин.
В этом случае неравенство (4.1) имеет вид F >
b
F
00
, где
матрица
b
F
00
получается из матрицы F
00
в результате
поразрядной д изъюнкци и строк, соответствующих
отождествляемым входам КС Σ
00
, и по-прежнему переходи т
в равенство, если КС Σ
00
разделительна по входам. В
последнем случае, кроме того, из аналогичного равенства,
связанного с КС
e
Σ
00
, котора я получается из КС Σ
00
в
результате объявления ее входов входами и, одновременно,
выходами
e
Σ
00
, следует разделительность КС Σ по входам.
Заметим, наконец, что стыковка общего вида Σ = Σ
00
(Σ
0
)
сводится к последовательному выпо лнен ию отождествления
входов вида
b
Σ
00
= Σ
00
ˇ
Σ
00
и бесповторной стыковки вида
Σ =
b
Σ
00
(
b
Σ
0
), где КС
ˇ
Σ
00
состоит из проводящей звезды
и тождественных вершин, а КС
b
Σ
0
получается из КС
Σ
0
снятием некоторых выходов. При этом неравенство
(в случае разделительности КС Σ
00
по входам равенство)
(4.1) для КС Σ, Σ
0
, Σ
00
вытекает из установленных выше
аналогичных соотношений для КС
b
Σ
00
,
ˇ
Σ
00
, Σ
00
и КС Σ,
b
Σ
0
,
b
Σ
00
в силу ассоциативности произвед ения матриц. Случай
разделительности КС Σ
0
по выходам р ассматри вается
аналогично.

§4. Операция суперпозиции. Разделительные КС 47
Лемма доказана.
Следствие 1. В случае разделительности КС Σ
00
по
входам в каждой вершине КС Σ, Σ = Σ
00
(Σ), которая
соответствует выходу КС Σ
0
, реализуется т от же самый
столбец ФАЛ, что и в КС Σ
0
.
Действительно, полагая v
0
= a
0
i
и v
00
= a
j
, где i ∈ [1, p],
а j ∈ [1, q], из (4.3) получим требуемое равенство f = f
0
j
.
Случай стыковки общего вида рассматривается аналогич но.
Следствие 2. Равенство (4.1) выполняется на любом
наборе значений БП, на котором КС Σ
00
разделительна по
входам или КС Σ
0
разделительна по выходам.
Стыковка (суперпози ция) КС вида Σ = Σ
00
(Σ)
0
называется правильной, если она удовлетворяет равенству
(4.1), и считается корректной, если она, кроме того,
удовлетворяет требованиям следствия 1 из леммы 4.1
1
Аналогичным образом определяется правильность и
корректность суперпозиции КС на заданном наборе
значений управляющих БП. Заметим, что при правильной
стыковке (1, p)-КС и (p, 1)-КС, реализующих строку и
столбец из ФАЛ
f
0
1
, . . . , f
0
p
и
f
00
1
, . . . , f
00
p
соответственно,
получается (1, 1)-КС, реализующая ФАЛ f
0
1
f
00
1
∨ ··· ∨ f
0
p
f
00
p
,
при правильном отождествлении входов (выходов) КС
в реализуемой ею матрице происходит поразрядная
дизъюнкция тех строк (соответственно ст олбц ов), которые
соответствуют отождествленным входам (соответственно
выходам) и т. п.
1
Эти определения соответствуют обычным определениям, если
считать, что F
00
(F
0
) = F
0
· F
00
. Требования следствия 1 леммы 4.1 не
распространяются, как правило, на тождественные вершины КС Σ
0
,
добавленные для согласования числа ее выходов с числом входов КС
Σ
00
.

48 Глава 2. Основные классы управл яющих систем
Легко видеть, что операции переименования в ходов без
отождествления, переименования выходов и объединения
корректны в любом случае. Из леммы 4.1 и ее следствий
вытекает, что для разделительной по входам КС Σ
00
любая
суперпозиция вида Σ
00
(Σ
0
) является корректной. Это
относится, в частности, к последовательному соединению
(1, 1)-КС (см. §5). В то же время параллельное соединение
(1, 1)-КС, при котором сначала отождествляются входы, а
затем выходы соединяемых КС, не является корректной
операцией суперпозиции, так как не удовлетворяет
требованиям сл едстви я 1 из леммы 4.1. Заметим,
что параллельное соединение КС является при этом
правильной суперпозицией, так как по лученн ая КС
реализует дизъюнкцию ФАЛ, реализуемых исходными
КС, и что корректное дизъюнктирование выходных ФАЛ
можно осуществить с помощью стыковки исходной КС с
вентильной звездой (см. рис. 4.3c).
•
•
x
2
:
:
:
:
:
:
:
:
:
•
x
1
:
:
:
:
:
:
:
:
:
•
x
1
•
x
2
•
x
1
x
1
:
:
:
:
:
:
:
:
:
a
00
a
00
1
a
00
2
a
00
3
•
•
x
2
:
:
:
:
:
:
:
:
:
•
x
1
:
:
:
:
:
:
:
:
:
•
x
1
•
x
2
x
1
•
x
2
x
1
a
00
a
00
1
a
2
a) b)
Рис. 4.5: отождествление входов у (3, 1)-КС Σ
00
В общем случае операции отождествления входов,
а также операции стыковки не всегда являются
правильными. Так, на рис. 4.5a изображена (3, 1) -КС
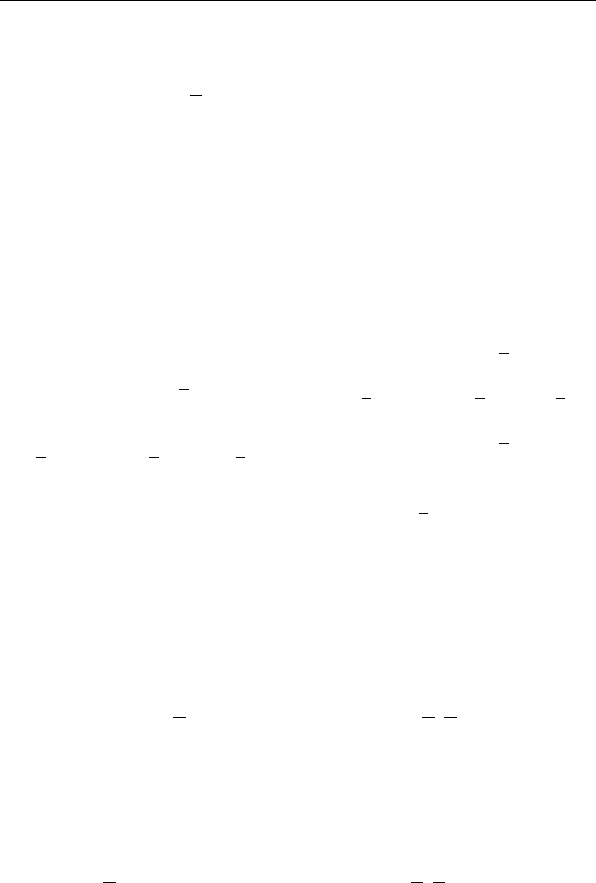
§4. Операция суперпозиции. Разделительные КС 49
Σ
00
(x
1
, x
2
; a
00
1
, a
00
2
, a
00
3
; a
00
), которая реализует столбец f
00
из
ФАЛ
f
00
1
= x
1
x
2
, f
00
2
= x
1
⊕ x
2
и f
00
3
= x
1
x
2
,
а на рисунке 4.5b — (2, 1)-КС
b
Σ
00
(x
1
, x
2
; a
00
1
, a
2
; a
00
), которая
получается из Σ
00
в результате отождествления входов a
00
2
=
= a
00
3
= a
2
и реализует столбец
b
f
00
из ФАЛ
b
f
00
1
= x
1
6= f
00
1
,
b
f
00
2
= x
1
∨ x
2
.
•
•
x
4
•
x
3
•
x
3
:
:
:
:
:
:
:
:
:
•
x
4
:
:
:
:
:
:
:
:
:
•
x
3
:
:
:
:
:
:
:
:
:
x
3
a
0
a
0
1
a
0
2
a
0
3
•
•
x
4
y
y
y
y
y
y
y
y
•
x
4
E
E
E
E
E
E
E
E
•
x
3
y
y
y
y
y
y
y
y
•
x
3
E
E
E
E
E
E
E
E
x
3
y
y
y
y
y
y
y
y
•
x
3
E
E
E
E
E
E
E
E
•
x
1
E
E
E
E
E
E
E
E
x
1
y
y
y
y
y
y
y
y
•
x
1
E
E
E
E
E
E
E
E
x
1
y
y
y
y
y
y
y
y
•
x
2
E
E
E
E
E
E
E
E
x
2
y
y
y
y
y
y
y
y
a
0
a
00
a) b)
Рис. 4.6: (1, 3)-КС Σ
0
и Σ = Σ
00
(Σ
0
)
На рис. 4.6a показана (1, 3)-КС Σ
0
(x
3
, x
4
; a
0
; a
0
1
, a
0
2
, a
0
3
),
которая реализует набор f
0
из ФАЛ
f
0
1
= x
3
x
4
, f
0
2
= x
3
∼ x
3
, f
0
3
= x
3
x
4
,
а на рис. 4.6b — (1, 1)-КС Σ(x
1
, x
2
, x
3
, x
4
; a
0
; a
00
), которая
является результатом бесповторной стыковки вида Σ
00
(Σ)
0
и реализует ФАЛ f (x
1
, x
2
, x
3
, x
4
) такую, что
f(x
1
, x
2
, x
3
, x
4
) =
= x
3
x
4
x
1
∨ (x
3
∼ x
4
) · (x
1
⊕ x
2
) ∨ x
3
x
4
x
1
x
2
6=
6= f
0
1
· f
00
1
∨ f
0
2
· f
00
2
∨ f
0
3
· f
00
3
.

50 Глава 2. Основные классы управл яющих систем
§5 Контактные схемы и
π-схемы, оценка их числа. Особенности
функционирования многополюсных
контактных схем
Рассмотрим класс контактных схем, в которых реализация
ФАЛ осуществляется не с помощью преобразования
входных значений в выходные, как это происходит,
например, в схемах из функциональных эл ементов (см.
§3), а в результате передачи значений по ребрам графа,
проводимостью которого «управляют» входные БП. Ребро
или дуга графа с пометкой x
i
(x
i
) называется замыкающим
(соответственно размыкающим) контактом БП x
i
(см. рис.
5.1).
a) b) c)
s s ss s s
v v vu u u
x
i
x
i
x
σ
i
-
Рис. 5.1: типы контактов
a) b)
v vu u
q qq qq qq q
q q
?
6
x
i
x
i
Рис. 5.2: физическая интерпретация контактов
Считается, что контакт вида x
σ
i
, σ ∈ {0, 1},
проводит тогда и только тогда, когда x
i
= σ, причем
ориентированный контакт, то есть контакт, связанный с
дугой, проводит только в соответствующем направлении.
