Логунов Евгений Леонидович (сост.) Полная шпаргалка по алгебре
Подождите немного. Документ загружается.

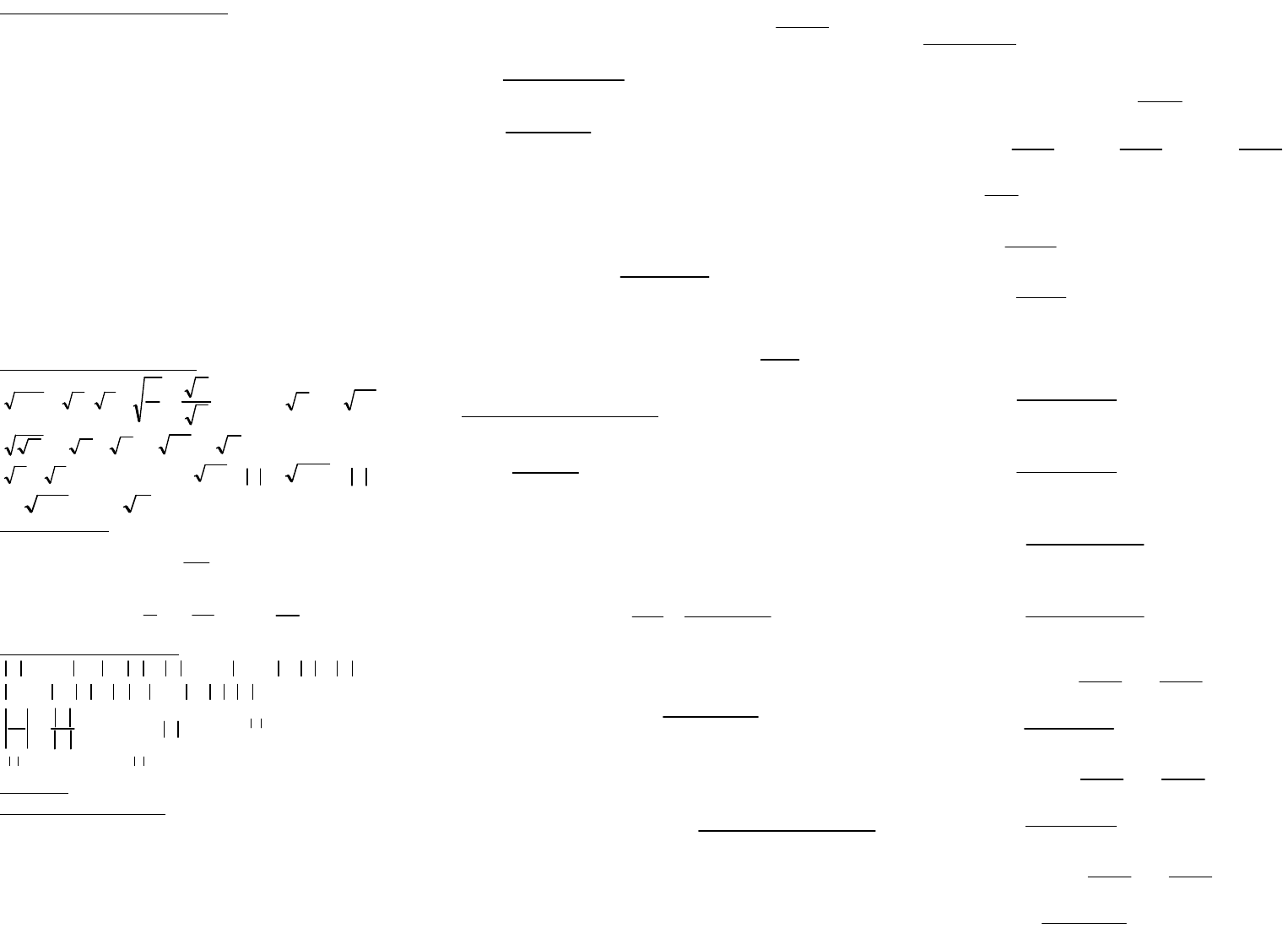
Формулы преобразования многочленов
)()(
22
bababa
,
bababa 2)(
222
,
bababa 2)(
222
,
222
2)( bbaaba
,
222
2)( bbaaba
,
)()(
2233
bbaababa
,
)()(
2233
bbaababa
,
)(3)(
333
babababa
,
32233
33)( bbabaaba
,
)(3)(
333
babababa
32233
33)( bbabaaba
,
)(3)(
333
babababa
,
)()(
21
2
xxxxacxbxa
, где
1
x
и
2
x
-
корни квадратного трёхчлена
cxbxa
2
.
Свойства арифметических корней
nnn
baba
,
)0( b
b
a
b
a
n
n
n
,
n
kk
n
aa )(
,
kn
n
k
aa
,
kn
k
n
aa
,
)0()( aaa
n
n
,
nn
ba
, если
ba 0
,
aa
2
,
aa
n n
2 2
,
1212
nn
aa
.
Свойства степеней
1
0
a
,
yxyx
aaa
,
yx
y
x
a
a
a
,
yxyx
aa
)(
,
xxx
baba )(
,
x
x
x
b
a
b
a
,
x
x
a
a
1
.
Модули действительных чисел
0x
,
xx
,
xx
,
yxyx
,
yxyx
,
yxyx
,
)0( , y
y
x
y
x
,
2
2
xx
,
ax
ax
a
ax
,
0
,
,
axa
a
ax
,0
,
,
ax
ax
a
ax
,
,0
,
Прогрессии
Арифметическая прогрессия (
1
a
- первый член,
d
- разность,
n
- число членов,
n
a
- n-й член,
n
S
- сумма n первых членов
прогрессии).
1
nn
aad
,
)1(
1
ndaa
n
,
n
aa
S
n
n
2
1
,
n
nda
S
n
2
)1(2
1
,
1nk
,
2
11
kk
k
aa
a
,
qpmk
aaaa
, где
qpmk
.
Геометрическая прогрессия (
1
b
- первый член,
q
- знаменатель (
0q
),
n
- число членов,
n
b
- n-й член (
0
n
b
),
n
S
-
сумма n первых членов прогрессии).
1
1
n
n
qbb
,
0)(q ,
1
)1(
1
q
qb
S
n
n
,
1)(q
1
bnS
n
,
11
2
nnn
bbb
,
qpmk
bbbb
, где
qpmk
;
1)(q
1
1
q
b
S
(сумма бесконечной геометрической прогрессии).
Комбинаторика и бином Ньютона
Число возможных размещений из n различных элементов по m:
- без повторений
)1(...)1(
)!(
!
mnnn
mn
n
A
m
n
,
- с повторениями
mm
n
nA
~
Число возможных перестановок из n элементов
!nP
n
Число возможных сочетаний из n различных элементов по m:
- без повторений:
!)!(
!
nmn
n
P
A
C
m
m
n
m
n
, где
1 ;
0
n
Cnm
,
mn
n
m
n
CC
,
1
1
1
m
n
m
n
m
n
CCC
.
- с повторениями:
)!1(!
)!1(
~
1
11
nm
mn
CCC
n
mn
m
mn
m
n
Бином Ньютона:
nn
n
kknk
n
n
n
n
n
n
bCbaCbaCaCba
......)(
110
, или
nkknnnn
bba
k
knnn
banaba
...
!
)1(...)1(
...)(
1
.
)1( k
-й член в разложении бинома:
kknk
nk
baCT
1
.
Сумма биноминальных коэффициентов:
nn
nnn
CCC 2...
10
.
Тригонометрия.
Формулы, связывающие тригонометрические функции одного
аргумента:
1cossin
22
xx
,
x
x
cos
1
sec
,
x
x
sin
1
eccos
,
x
x
xtg
cos
sin
,
x
x
xctg
sin
cos
,
xtg
xctg
1
,
1 xctgxtg
,
x
x
xtg
2
2
2
sec
cos
1
1
,
x
x
xc tg
2
2
2
eccos
sin
1
1
.
Тригонометрические функции сумм и разностей двух различных
аргументов:
yxyxyx sinsincoscos)cos(
,
ytgxtg
ytgxtg
yxtg
1
)(
,
yxyxyx sinsincoscos)cos(
,
ytgxtg
ytgxtg
yxtg
1
)(
,
yxyxyx sincoscossin)sin(
,
yctgxctg
yctgxctg
yxctg
1
)(
,
yxyxyx sincoscossin)sin(
,
yctgxctg
yctgxctg
yxctg
1
)(
.
Суммы и разности тригонометрических функций аргументов:
2
cos
2
sin2sinsin
yxyx
yx
,
yx
yx
ytgxtg
coscos
)sin(
,
2
cos
2
sin2sinsin
yxyx
yx
,
yx
yx
ytgxtg
coscos
)sin(
,
2
cos
2
cos2coscos
yxyx
yx
,
yx
yx
yctgxctg
sinsin
)sin(
,
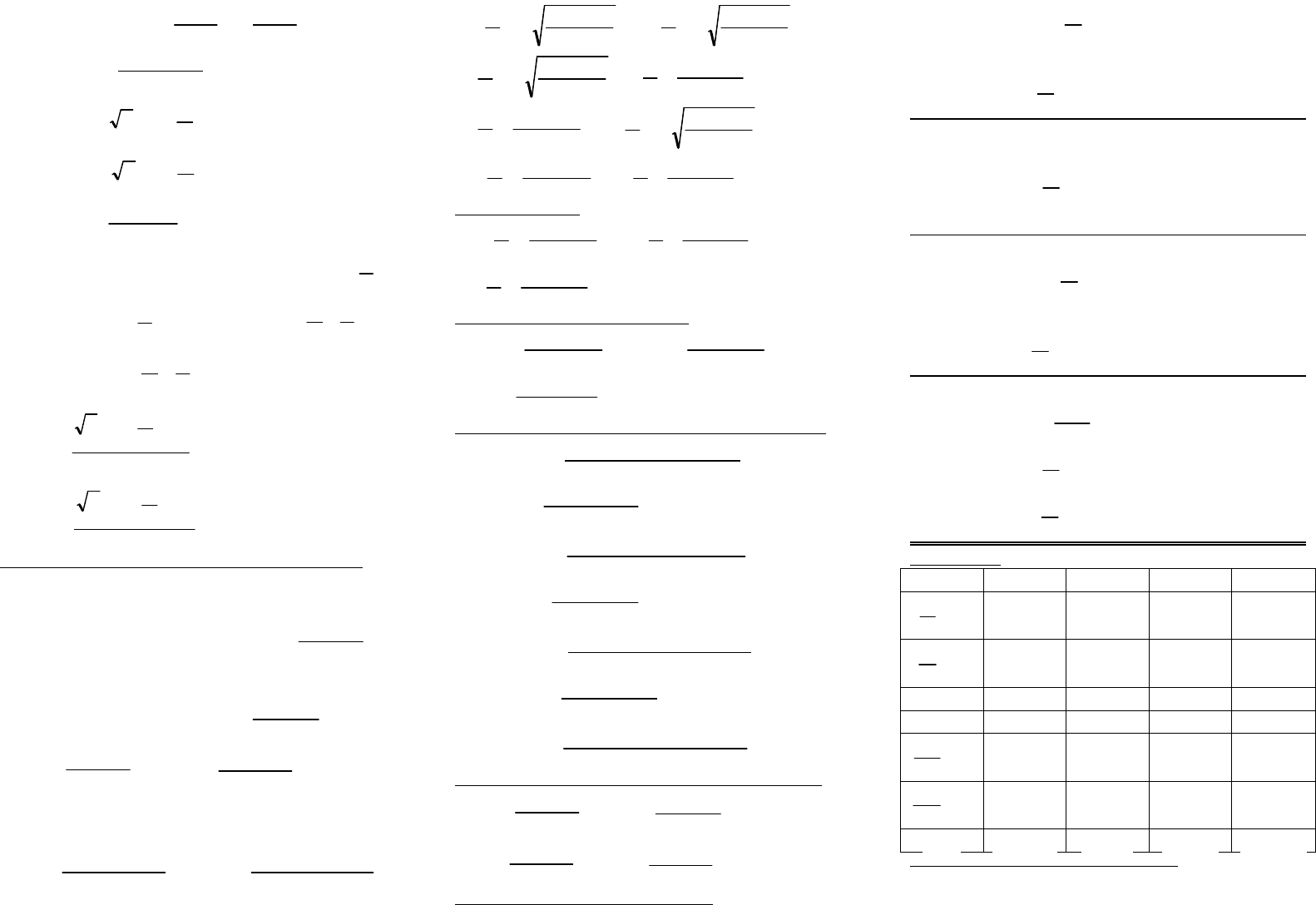
2
sin
2
sin2coscos
yxyx
yx
,
yx
xy
yctgxctg
sinsin
)sin(
,
xxx
4
cos2sincos
,
xxx
4
sin2sincos
,
)2sin(
2
x
xctgxtg
,
)(2 2 xctgxctgxtg
,
2
cos2cos1
2
x
x
,
2
sin2cos1
2
x
x
,
24
cos2sin1
2
x
x
,
24
sin2sin1
2
x
x
,
x
x
xtg
cos
4
sin2
1
,
x
x
xtg
cos
4
sin2
1
.
Тригонометрические функции двойного и кратных аргументов:
xxx cossin22sin
,
1)cos(sin2sin
2
xxx
,
2
)cos(sin12sin xxx
,
xtg
xtg
x
2
1
2
2sin
;
xxx
22
sincos2cos
,
xx
2
sin212cos
,
1cos22cos
2
xx
,
xtg
xtg
x
2
2
1
1
2cos
;
xtg
xtg
xtg
2
1
2
2
,
xctg
xctg
xctg
2
1
2
2
;
xxx
3
sin4sin33sin
,
xxx cos3cos43cos
3
,
xtg
xtgxtg
xtg
2
3
31
3
3
,
13
3
3
2
3
xctg
xctgxctg
xctg
;
2
cos1
2
sin
xx
,
2
cos1
2
cos
xx
,
x
xx
tg
cos1
cos1
2
,
x
xx
tg
cos1
sin
2
,
x
xx
tg
sin
cos1
2
,
x
xx
ctg
cos1
cos1
2
,
x
xx
ctg
cos1
sin
2
,
x
xx
ctg
sin
cos1
2
.
Формулы понижения:
2
cos1
2
sin
2
xx
,
2
cos1
2
cos
2
xx
,
x
xx
tg
cos1
cos1
2
2
.
Квадраты тригонометрических функций:
2
2cos1
sin
2
x
x
,
2
2cos1
cos
2
x
x
,
x
x
xtg
2cos1
2cos1
2
.
Произведения тригонометрических функций разных аргументов:
2
)sin()sin(
cossin
yxyx
yx
,
yctgxctg
ytgxtg
ytgxtg
,
2
)sin()sin(
sincos
yxyx
yx
,
ytgxctg
yctgxtg
yctgxtg
,
2
)cos()cos(
coscos
yxyx
yx
,
ytgxtg
yctgxctg
yctgxctg
,
2
)cos()cos(
sinsin
yxyx
yx
.
Выражение тригонометрических функций через одну, где a =x/2:
atg
atg
x
2
1
2
sin
,
atg
atg
x
2
2
1
1
cos
,
atg
atg
xtg
2
1
2
,
atg
atg
xctg
2
1
2
.
Простейшие тригонометрические уравнения:
Znnaxax
n
,arcsin)1( sin
Znnxx ,2
2
1sin
Znnxx , 0sin
Znnxx ,2
2
1sin
Znnaxax ,2arccos cos
Znnxx ,2 1cos
Znnxx ,
2
0cos
Znnxx ,2 1cos
Znnaarctgxaxtg ,
Znnxxtg ,
4
1
Znnxxtg , 0
Znnxxtg ,
4
1
Znnaarcctgxaxctg ,
Znnxxctg
,
4
3
1
Znnxxctg ,
2
0
Znnxxctg ,
4
1
Формулы приведения
u
usin
ucos
utg
uctg
x
2
xcos
xsin
xctg
xtg
x
2
xcos
xsin
xctg
xtg
x
xsin
xcos
xtg
xctg
x
xsin
xcos
xtg
xctg
x
2
3
xcos
xsin
xctg
xtg
x
2
3
xcos
xsin
xctg
xtg
x
xsin
xcos
xtg
xctg
Знаки значений тригонометрических функций:
Синус Косинус Тангенс и котангенс
+ + - + - +
- - - + + -
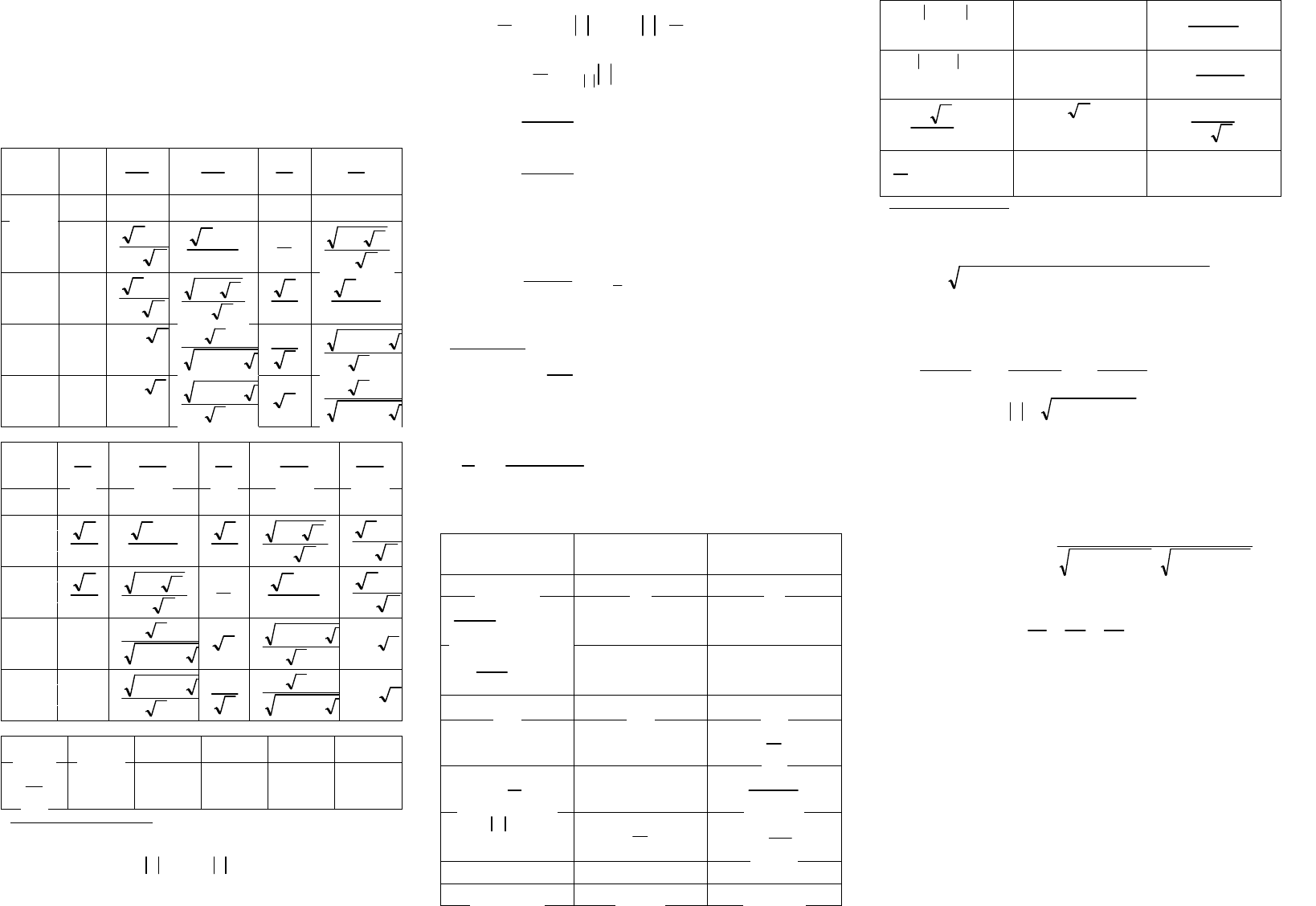
Значения тригонометрических функций
некоторых углов
рад
0
12
10
6
5
град
0
15
18
30
36
sin
0
22
13
4
15
2
1
22
55
cos
1
22
13
22
55
2
3
4
15
tg
0
32
5210
15
3
1
15
5210
ctg
-
32
15
5210
3
5210
15
рад
4
10
3
3
5
2
12
5
град
45
54
60
72
75
sin
2
2
4
15
2
3
22
55
22
13
cos
2
2
22
55
2
1
4
15
22
13
tg
1
5210
15
3
15
5210
32
ctg
1
15
5210
3
1
5210
15
32
рад
град
sin
cos
tg
ctg
2
90
1 0 - 0
Логарифмы и их свойства
ba
b
a
log
,
01log
a
,
1log a
a
,
0 ,loglog)(log cbcbcb
aaa
0 ,logloglog
c
b
cb
c
b
aaa
,
0 ,0 ,loglog kbb
k
n
b
n
a
n
a
k
,
1 ,0 ,0 ,
log
log
log cbc
a
b
b
c
c
a
,
1 ,0 ,
log
1
log bb
a
b
b
a
,
1c ,0,, ,
loglog
cbaba
ab
cc
,
bb lglog
10
,
bb
e
lnlog
,
bpb
a
p
a
loglog
,
m
b
b
a
a
m
log
log
,
bb
a
a
loglog
1
,
bpbb
pp
a
p
a
a
logloglog
.
Производная:
x
f
xf
x
0
lim)(
,
vuvu
)(
,
vuvuvu
)(
,
2
v
vuvu
v
u
,
ucuc
)(
.
Таблица производных и первообразных
некоторых функций:
Первообразная
)(xF
Функция
)(xf
Производная
)(xf
Cxa
a
0
1 ,
1
1
pC
p
x
p
Rpx
p
,
1
p
xp
C
a
a
x
ln
x
a
aa
x
ln
x
e
x
e
x
e
Cxxx ln
xln
x
1
C
e
x
x
a
log
x
a
log
ax ln
1
Cx ln
x
1
2
1
x
Cx cos
xsin
xcos
Cx sin
xcos
xsin
Cx cosln
xtg
x
2
cos
1
Cx sinln
xctg
x
2
sin
1
C
x
3
2
3
x
x2
1
0 ),(
1
abxaF
a
)( bxaf
)( bxafa
Векторы в пространстве:
Расстояние между 2-мя точками с координатами
);;(
1111
zyxA
и
);;(
2222
zyxA
:
2
12
2
12
2
1221
)()()( zzyyxxAA
.
Координаты середины отрезка с концами
);;(
1111
zyxA
и
);;(
2222
zyxA
:
2
,
2
,
2
212121
zz
z
yy
y
xx
x
. Модуль вектора
);;(
321
aaaa
:
2
3
2
2
2
1
aaaa
. Сложение и умножение
векторов:
);;();;();;(
332211221321
bababacbbbbaaaa
,
);;();;(
321321
aaaaaa
. Скалярное
произведение векторов:
332211
babababa
. Косинус
угла между векторами:
2
3
2
2
2
1
2
3
2
2
2
1
332211
cos
bbbaaa
bababa
.
Условие перпендикулярности векторов:
0ba
, параллельности
векторов:
ba
или
3
3
2
2
1
1
b
a
b
a
b
a
. Общее уравнение
плоскости, перпендикулярной вектору
);;( cban
:
0)()()(
000
zzcyybxxa
. Сфера радиуса R
задаётся уравнением:
2222
Rzyx
.
