Лиман С.А. Геодезия
Подождите немного. Документ загружается.

КАФЕДРА МАРКШЕЙДЕРИИ, ГЕОЛОГИИ И ГЕОДЕЗИИ
Дисциплина
"ГЕОДЕЗИЯ"
КОНСПЕКТ ЛЕКЦИЙ
С.А. Лиман
Для студентов строительных специальностей
заочной формы обучения
Объем издания – 91 с.
Алчевск
ДонГТУ
2005
2
1 ОБЩИЕ СВЕДЕНИЯ
1.1 Виды геодезических дисциплин
Высшая геодезия решает задачи по изучению фигуры и размеров Земли и пла-
нет, а также по созданию геодезических опорных сетей. При подробном изучении мето-
дов решения задач высшей геодезии из нее выделяются в отдельные дисциплины геоде-
зическая астрономия, геодезическая гравиметрия и космическая геодезия. Геодезическая
астрономия занимается вопросами определения исходных данных для опорных геоде-
зических сетей на основе наблюдения небесных светил. Геодезическая гравиметрия за-
нимается изучением фигуры Земли путем измерения с помощью специальных приборов
силы тяжести в отдельных точках земной поверхности. Космическая (спутниковая) гео-
дезия изучает геометрические соотношения между точками земной поверхности с по-
мощью искусственных спутников Земли.
Геодезия или топография изучает вопросы, связанные со съемками сравнитель-
но небольших участков земной поверхности и их детальным изображением в виде пла-
нов и карт.
Картография изучает методы и процессы создания изображений значительных
территорий земной поверхности в виде карт различного назначения, технологию их
производства и размножения.
Фототопография занимается разработкой методов создания планов и карт по
фотоснимкам и аэрофотоснимкам местности.
Морская геодезия разрабатывает методы специальных измерений, связанных с
картографированием и изучением природных ресурсов дна морей и океанов.
Прикладная геодезия занимается изучением методов геодезических работ, вы-
полняемых при изысканиях, строительстве и эксплуатации инженерных сооружений,
монтаже оборудования. Прикладная геодезия широко использует методы геодезии, а в
отдельных случаях – и свои приемы и средства.
1.2 Процессы производства геодезических работ
Геодезические работы подразделяются на полевые и камеральные. Полевые рабо-
ты – это процесс измерений, а камеральные – вычислительные работы и графические по-
строения.

3
Измерительный процесс состоит из угловых и линейных измерений на местности,
определения превышений, для чего применяются геодезические приборы - теодолиты,
нивелиры, дальномеры, ленты, рулетки, рейки и т.д. Результаты измерений заносят в
журналы, часто одновременно ведут схематические чертежи – абрисы.
Вычислительный процесс – математическая обработка, для чего применяют ЭВМ,
микрокалькуляторы, таблицы и т.п.
Графический процесс заключается в составлении на основе результатов измере-
ний и вычислений чертежей, планов - в соответствии с условными обозначениями и хо-
рошего качества.
1.3 Единицы измерений, применяемые в геодезии
При производстве геодезических измерений применяют меры: длины, площади,
массы, температуры, давления, угловые меры и т.д.
Линейные измерения в СНГ производятся в метрической мере, за единицу длины
принят метр. Длина метра была определена из результатов градусных измерений фран-
цузскими учеными Мишеню и Деламбром и в 1799 г. принята условно как 1:40 000 000
Парижского меридиана. На этом основании был изготовлен эталонный платино-
иридиевый жезл соответствующей длины «архивный метр», но он оказался на 0,21 мм
короче задуманного, поэтому его длина является эталоном при температуре, равной
0
0
С.
В 1875-1889 г.г. из платино-иридиевого сплава был изготовлен 31 жезл, из кото-
рых Россия получила 2 (№ 11 и № 28). № 28 хранится во ВНИМИ метрологии им.
В.И.Менделеева в Ленинграде и является эталоном в нашей СНГ. С 1960 г. утвержден
новый стандарт - равен 1650763,73 длины волны оранжевой линии спектра излучения
атома изотопа криптона-86 в вакууме.
Для точного определения мерных приборов 3-метровые жезлы из инвара (64 %
железа и 36 % никеля), длины которых определены государственным эталоном (№ 28). 1
м = 100 см = 1000 мм. 1/1000 мм = 1 микрону (мкм). Единица угловой величины – 1
0
=
1/90 прямого угла. 360
0
– окружность. 1
0
= 60′; 1′ = 60″.
ℓ = 2nR– содержит 2n радиан, поэтому 1 радиан равен ρ = 57,3
0
= 3438′ = ρ = 206265″.
Единицей S = 1 м
2
. 10 000 м
2
= 1 га. 1 000 000 м
2
= 100 га = 1 км
2
.

4
2 ФОРМА И РАЗМЕРЫ ЗЕМЛИ
Представление о форме Земли в целом можно получить, если вообразить, что вся
планета ограничена поверхностью Мирового океана в спокойном состоянии, непрерыв-
но продолженной под материками. Такая замкнутая поверхность, в каждой своей точке
перпендикулярная к отвесной линии, называется уровенной поверхностью.
Уровенных поверхностей, огибающих Землю, можно вообразить множество. Та
из них, которая совпадает со средним уровнем вод морей и океанов в спокойном состоя-
нии, образует фигуру, которая в геодезии принята за общую фигуру Земли, называемую
геоидом. Фигура геоида определяется направлением отвесных линий, положение кото-
рых зависит от распределения масс в земной коре. Вследствие невозможности определе-
ния истинного распределения масс внутри Земли поверхность геоида нельзя представить
каким либо конечным математическим уравнением. Поэтому возникла необходимость
замены поверхности геоида математически правильной и как можно ближе подходящей
к ней поверхностью.
Путем точных геодезических, астрономических и гравиметрических измерений
установлено, что по форме поверхность геоида наиболее близко подходит к математиче-
ской поверхности эллипсоида вращения. Размеры земного эллипсоида характеризуются
длинами его полуосей а (большая полуось) и b (малая полуось) и полярным сжатием:
a
ba
−
=α
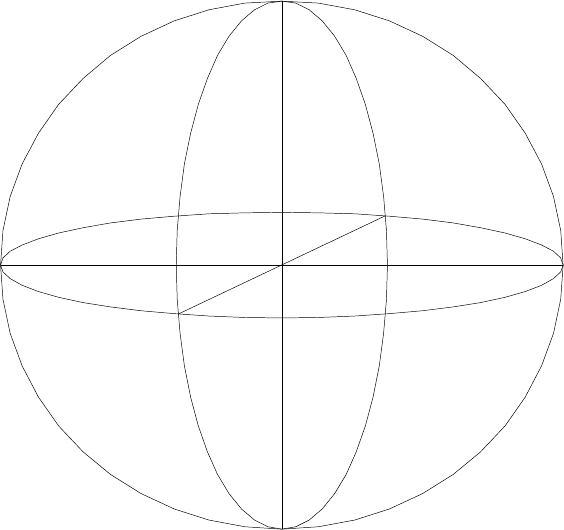
Линии сечения поверхности сфероида плоскостями, проходящими через ось вра-
щения, называются меридианами и представляют собой эллипсы (рис. 2.1). Линии сече-
ния поверхности сфероида плоскостями, перпендикулярными к оси вращения, называ-
ются параллелями и являются окружностями. Параллель, плоскость которой проходит
через центр сфероида, называется экватором.
Изучение фигуры Земли сводится в первую очередь к определению размеров по-
луосей и сжатия эллипсоида, наилучшим образом подходящего к геоиду и правильно
ориентированного в теле Земли. Такой эллипсоид называется референц-эллипсоидом.
Размеры земного эллипсоида неоднократно определялись учеными разных стран.
До 1946 г. в СССР пользовались эллипсоидом Бесселя (а=6377397 м, b=6356079 м,
α=1:299,2). Однако эллипсоид Бесселя на территории СССР (особенно в восточных его
5
районах) значительно отходит от поверхности геоида. В 1940 г. советскими учеными
были получены размеры эллипсоида, наиболее подходящие для территории СССР
(а=6378245 м, b=6356863 м, α=1:298,3). Эллипсоид указанных размеров с 1946 г. принят
для геодезических работ в СССР и назван эллипсоидом Красовского по фамилии руко-
водителя работ. Эллипсоид Красовского используется и на территории Украины в на-
стоящее время. Размеры эллипсоида Красовского, полученные из обработки геодезиче-
ских, астрономических и гравиметрических материалов градусных измерений СССР,
Западной Европы и США, являются наиболее обоснованными как по объему использо-
ванных материалов, так и по строгости их обработки.
b
a
Рисунок 2.1 – Земной эллипсоид.
В настоящее время изучение физической поверхности Земли производится путем
определения положения точек местности относительно расположенной некоторым обра-
зом поверхности (поверхности относимости), за которую принимается поверхность ре-
ференц-эллипсоида Красовского.
3 СИСТЕМЫ КООРДИНАТ, ПРИМЕНЯЕМЫЕ В ГЕОДЕЗИИ
Положение точек физической поверхности Земли определяется координатами –
величинами, характеризующими расположение искомых точек относительно исходных
6
плоскостей, линий и точек, определяющих выбранную систему координат. Все системы
координат, применяемые в геодезии, могут быть разделены на две группы: пространст-
венные и плоские.
3.1 Пространственные системы координат.
Географическая система координат объединяет под общим названием две сис-
темы – астрономическую и геодезическую. В астрономической системе координаты то-
чек определяются относительно направлений отвесных линий в точках земной поверх-
ности, а в геодезической - относительно нормалей к референц-эллипсоиду. Астрономи-
ческие координаты могут быть измерены техническими средствами и методами геоде-
зической астрономии. Геодезические координаты точек получают путем вычислений по
формулам сферической геодезии соответственно параметрам принятого референц-
эллипсоида и его ориентировки в теле Земли. Эти системы связаны между собой через
уклонение отвесных линий – угол между направлениями нормали к поверхности эллип-
соида и отвесной линии в данной точке. Величины уклонений зависят от неравномерно-
стей распределения масс в теле Земли и составляют в среднем 3-4”, достигая в отдель-
ных аномальных районах (как правило, в горных) десятков секунд.
Элементами географической системы координат являются: плоскость экватора;
ось вращения Земли, перпендикулярная к экватору; плоскость начального меридиана, за
который по международному соглашению принят Гринвичский меридиан, проходящий
через главный зал Гринвичской обсерватории близ Лондона.
Положение проекции точки А на поверхности эллипсоида определяется коорди-
натами – геодезическими широтой В и долготой L.
Геодезической широтой В называется угол, образованный нормалью к поверхно-
сти эллипсоида в данной точке и плоскостью экватора (рис. 2.2). Широта измеряется ду-
гой геодезического меридиана от экватора до данной точки и в зависимости от полуша-
рия может быть северной (+) и южной (–) и изменяется от 0
0
на экваторе до ±90
0
на по-
люсах.
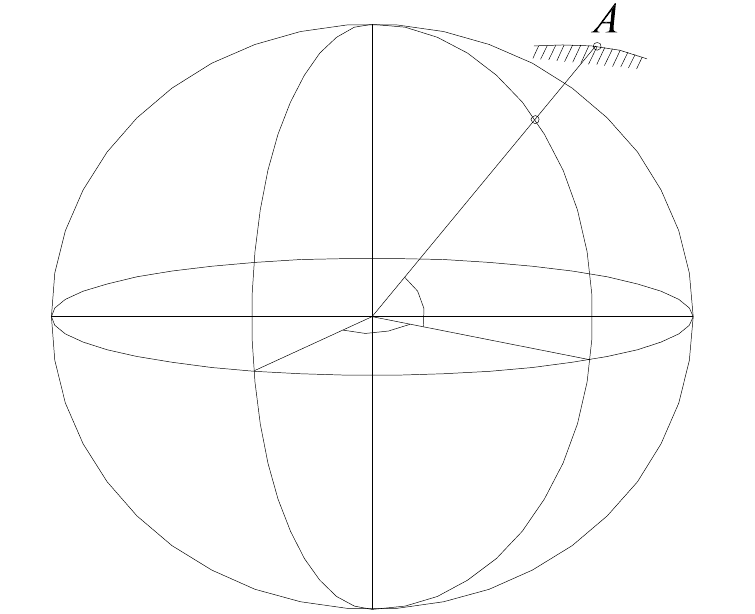
7
B
L
A'
Рисунок 3.1 – Схема определения геодезических координат.
Геодезической долготой L называется двугранный угол, составленный плоско-
стями начального меридиана и геодезического меридиана данной точки. Долгота изме-
ряется дугой экватора либо параллели от Гринвичского меридиана до меридиана данной
точки. Она изменяется от 0
0
до ±180
0
и может быть западной (–) или восточной (+).
Положение точки А на физической поверхности Земли определится координата-
ми B, L и высотой Н, характеризующей отстояние по нормали данной точки от ее про-
екции на поверхности эллипсоида.
Географическая система координат является единой для всего земного шара. Она
широко применяется при решении задач астрономии, сферической геодезии, картогра-
фии, охватывающих большие пространства.
3.2 Плоские системы координат.
Из плоских систем координат в геодезии наибольшее распространение получили
система прямоугольных координат и полярная система координат. Указанные системы
координат применяются при производстве съемочных работ и изображении участков
земной поверхности на плоскости в виде планов и карт.
8
3.2.1 Плоская система прямоугольных координат. Если размеры участка земной
поверхности позволяют не принимать во внимание сферичность Земли, то при произ-
водстве геодезических работ часто применяется условная система плоских прямоуголь-
ных координат, начало которой выбирается произвольно.
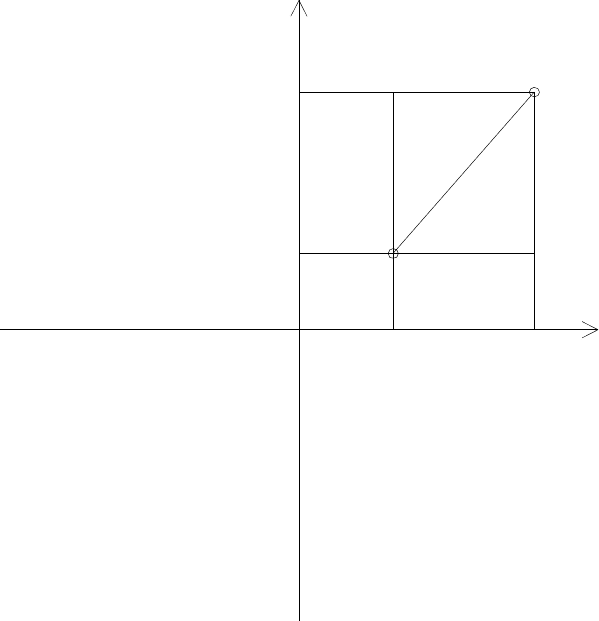
Элементами данной системы координат являются (рис. 3.2) ось ОХ, направление
которой принимается параллельным истинному, магнитному или осевому меридиану
зоны либо произвольным; ось ОY, перпендикулярная к оси ОХ; точка О – начало коор-
динат. Координаты точек равны расстояниям от начала координат до проекции этих то-
чек на оси.
Проекции линии на оси координат называются приращениями координат и обо-
значаются ∆X и ∆Y. Знаки приращений зависят от четверти. Если известны координаты
X
A
и Y
A
точки А и приращения координат ∆X и ∆Y между точками А и В, то координа-
ты точки В будут равны:
Х
В
= Х
А
+ ∆X
Y
B
= Y
A
+ ∆Y.
Данная система координат применяется при горизонтальных съемках и состав-
лении планов местности.
3.2.2 Зональная система плоских прямоугольных координат. При топографиче-
ских съемках, маркшейдерских и инженерно-геодезических работах наиболее целесооб-
разно применять системы плоских прямоугольных координат. Поэтому для изображения
на плоскости значительных территорий земной поверхности применяются картографи-
ческие проекции, дающие возможность переносить точки с поверхности эллипсоида на
плоскость по определенным математическим законам. В геодезии применяются такие
проекции эллипсоида на плоскость, которые не искажали бы углов. Подобные проекции
называются равноугольными или конформными. Возникающие при этом искажения
длин и площадей должны быть незначительными и учитываться простыми формулами.
9
0
X
Y
A
B
X
X
Y
Y
A
A
B
B
Y
X∆
∆
Рисунок 3.2 – Плоская условная система прямоугольных координат.
Искажения будут тем больше, чем обширнее участок поверхности эллипсоида,
проектируемый на плоскость. Для того, чтобы поправки за искажение длин были срав-
нительно невелики, при изображение больших областей поверхности эллипсоида их де-
лят на отдельные участки (зоны) и каждый из них изображается на плоскости в своей
системе прямоугольных координат.
В общегосударственной системе плоских прямоугольных координат положение
точек земной поверхности определяется координатами X и Y на плоскости, на которую
они проектируются по закону равноугольной поперечно-цилиндрической проекции Га-
усса-Крюгера.
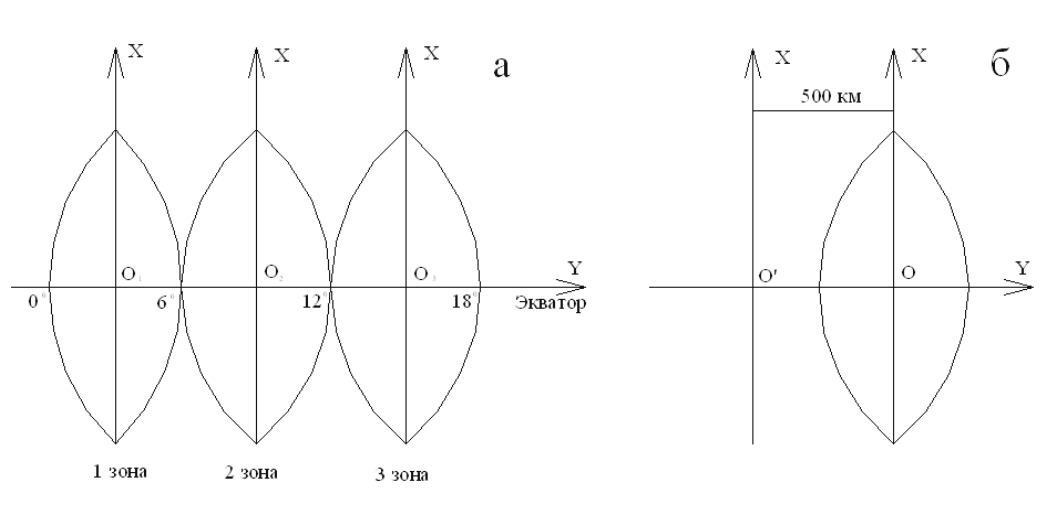
Сущность проекции Гаусса-Крюгера заключается в следующем. Земной эллипсо-
ид делится меридианами через 6
0
по долготе на 60 зон, простирающихся от полюса до
полюса (рис. 3.3 а). Нумерация зон ведется с запада на восток от Гринвичского меридиа-
на, который является западной границей первой зоны. Средний меридиан каждой зоны
называется осевым.
10
Осевой меридиан зоны изображается на плоскости прямой линией и принимает-
ся за ось абсцисс (Х); осью ординат (Y) является изображение экватора. На территории
Украины, полностью расположенной в северном полушарии, абсциссы всегда положи-
тельны. Ординаты же могут быть как положительными, так и отрицательными. Чтобы
избежать отрицательных значений ординат, ось Х условно переносят на 500 км к западу
от осевого меридиана (рис. 3.3 б). Исправленную таким образом ординату называют
приведенной (Y).
где а – схема изображения зон после развертки на плоскости;
б – схема определения приведенных координат.
Рисунок 3.3 – Зональная система прямоугольных координат.
В каждой из 60 зон численные значения координат X и Y могут повторятся. По-
этому для однозначного определения положения точки на земной поверхности перед
каждой ординатой ставится номер зоны.
Зональная система плоских прямоугольных координат находит самое широкое
применение при составлении планов и карт территории нашей страны.
3.2.3 Система плоских полярных координат. Элементами данной системы коор-
динат являются полярная ось ОХ (за ось ОХ может приниматься любое направление,
например сторона теодолитного хода); точка О - начало координат или полюс (обычно
за полюс принимается точка теодолитного хода).
