Лекция №8 - Теория установившегося неравномерного движение жидкости в открытых руслах
Подождите немного. Документ загружается.


Лекция №8
Тема8. ТЕОРИЯ УСТАНОВИВШЕГОСЯ НЕРАВНОМЕРНОГО
ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ
Рассматриваемые вопросы:
8.1. Непризматические и призматические русла.
8.2. Исследование дифференциального уравнения движения жидкости, форм свободной
поверхности потока.
8.3 Построение кривых свободной поверхности в искусственных руслах.
8.1. Непризматические и призматические русла
Задача неравномерного движения заключается в определении очертаний
кривых подпора (рис. 8.1.а), и спада (рис.8.1б), т.е. в вычислении глубины h в
заданном поперечном сечении русла или в нахождении месторасположения
сечения с заданной глубиной.
а) б)
h
L
h
L
Рис.8.1.
При неравномерном движении жидкости гидравлические элементы потока
изменяются по его длине. Уклоны I
0
, поверхности воды I и гидравлический I
г
имеют разные значения (I
0
≠
I I
≠
г
).
Причины. Изменение размеров и форм живых сечений по длине потока,
воздействием га поток сооружений (гидротехнических, мостовых переходов и
др.).
Русла подразделяются на призматические и непризматические. В
последнем случае размеры и форма русла изменяются по длине потока -
, где h –глубина потока; l -расстояние, отсчитываемое по длине
потока от начального сечения. В призматических руслах его форма не зависит от
длины l, потому →
)l,h(ω=ω
)h(ω=ω
0
l
=
∂
ω∂
.
8.2. Исследование дифференциального уравнения движения жидкости,
форм свободной поверхности потока
При неравномерном движении воды дифференциальные уравнения имеют
вид:

Rc
v
)
g2
v
(
dl
d
I
2
22
+
α
= , (8.1)
зная то, что
ω
=
Q
v
, и
R
ω
c
=K
2
2
2
2
K
Q
)
g2
Q
(
dl
d
I +
ω
α
= ; (8.2)
где I –представляет собой уклон поверхности воды, K - расходная
характеристика при неравномерном движении (изменяется по длине потока).
Одной из основных задач теории неравномерного движения является
исследование изменения глубины потока по длине. Последнее уравнение
преобразуют так, чтобы в него входила производная
dl
dh
.
Линия пресечения свободной поверхности потока с продольной
вертикальной поверхностью называется кривой свободной поверхности потока.
Если
dl
dh
>0, то глубина потока увеличивается вниз по течению, и кривая
свободной поверхности называется кривой подпора. Если
dl
dh
<0, то глубина
уменьшается и кривая свободной поверхности называется кривой спада.
Основные параметры для расчета показаны на рис.8.2.
l
z
zo
g2
v
2
α
h
l
0
I
α
0
h
l
г
I
I
Рис.8.2.
Где z = h+(z
0
-J
0
l), h-глубина неравномерного потока, z
0
-отметка для
потока,
z
0
=const при изменении z и h, J
0
=Sin -уклон для потока.
0
α
Второй вид уравнения
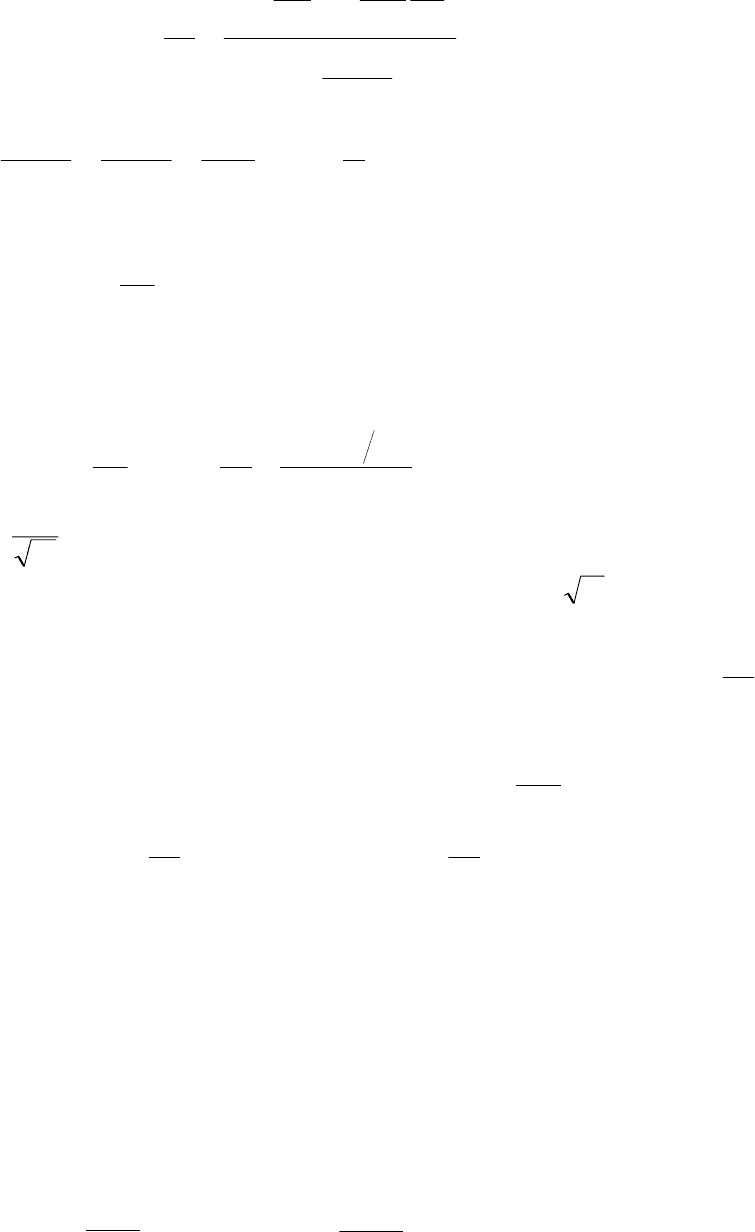
3
2
32
2
0
g
BQ
1
)
l
g
K
1(
K
Q
I
dl
dh
ω
α
−
∂
ω∂
ω
α
−−
= , (8.3)
где
r
ср
2
2
3
3
3
F
gh
g
BQ
g
BQ
=
αυ
=
ωω
α
=
ω
α
;
ср
h
B
=
ω
-средняя глубина потока; F
r
-число
Фруда.
Другая запись F
r
=
gl
u
2
-характеризует соотношение инерционных сил и сил
тяжести в потоке жидкости.
Дифференциальное уравнение неравномерного движения жидкости в
призматических руслах
dl
dω
=0;
→
r
22
0
F1
KQI
dl
dh
−
−
= , (8.4)
где
0
0
K
I
Q
=
-расходная характеристика при равномерном движении при
том же расходе, что и при неравномерном движении;
KRc
=ω
.
Далее проводят исследование с помощью дифференциального уравнения.
О форме кривой свободной поверхности потока судят по значению
dl
dh
, т.е. по
величине тангенса угла между касательной к кривой и линией дна в отдельных
точках, а также по знаку второй производной
2
2
dl
hd
в этих точках. Если
выполняется условие
dl
dh
>0 - кривые подпора,
dl
dh
<0 - кривые спада.
Существует 12 форм свободной поверхности потока.
8.2.1. Критическая глубина, бурное, критическое и спокойное состояние
потока
Общие положения
Удельная энергия в данном живом сечении безнапорного потока
относительно горизонтальной плоскости, проходящей через низшую точку этого
сечения, без учета удельной энергии, соответствующей атмосферному давлению,
называется удельной энергией сечения.
Э=h+
g2
v
2
α
или Э=h+
2
2
g2
Q
ω
α
(8.5)
Исследование Э при Q=const.
При h
→
0; Э , следовательно ось абсцисс (рис 8.3) должна
быть асимптотой кривой Э=Э(h).
0→ω
⇒ ∞→
При h
→
; и Э
→
, а уравнение удельной энергии сечения
принимает вид Э=h, т.к. второй член справа формулы (8.5) стремится к нулю.
∞
ω
∞→ ∞
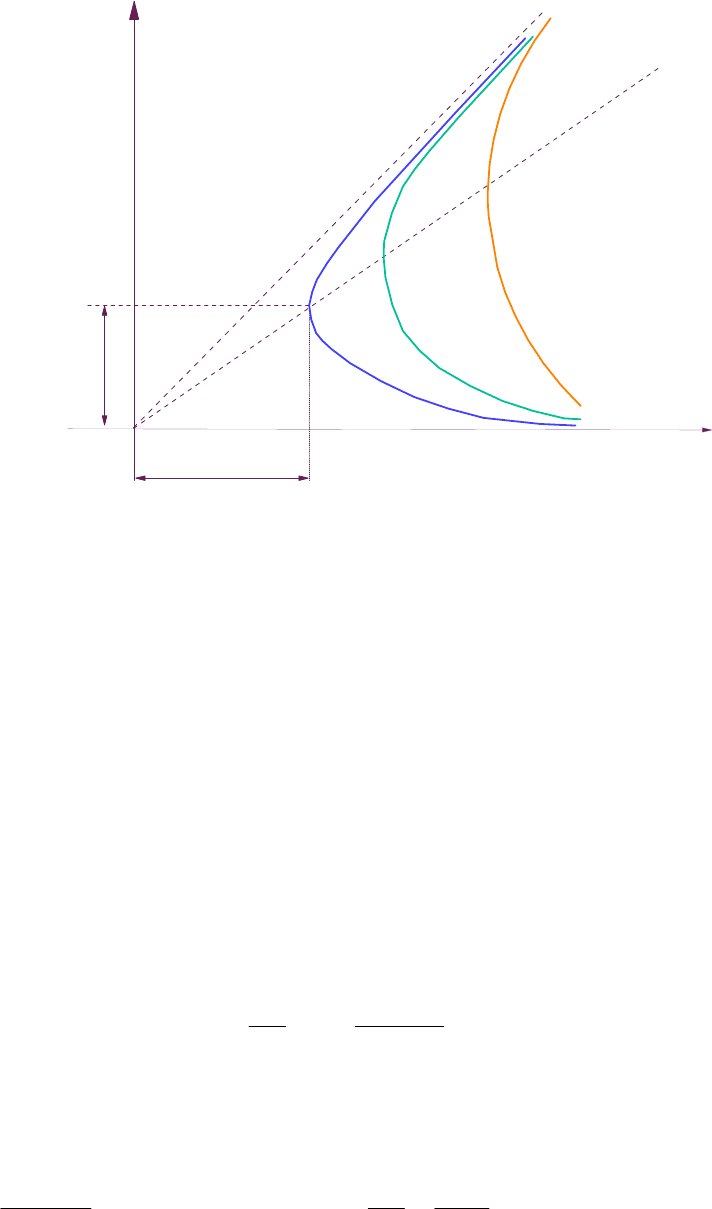
Следовательно, второй асимптотой будет биссектриса координатного угла. Так
как Э=Э(h) на границах принимает значения
, то при некотором h она
должна иметь минимум.
∞+
2
Э=Э(h) называется графиком удельной энергии сечения.
h
1К
h
Fr
к
=1
Fr
к
>1
Fr
к
<1
Q
1
<
Q
2
<
Q
3
Э
мин1
Э
Рис.8.3.
Глубину потока h
к
, при которой заданный расход воды проходит с
минимальным значением удельной энергии сечения (Э=Э
мин
), называется
критической глубиной. Состояние потока, при котором его глубина равна
критической (h=h
к
), называется критическим состоянием потока. Точка на
кривой удельной энергии сечения при Э=Э
мин
разделяет ее на две ветви. Нижняя
отвечает такому течению, при котором с уменьшением глубины удельная
энергия сечения уменьшается (dЭ/dh<0). Состояние потока, при котором его
глубина меньше критической (h<h
к
), называется бурным состоянием потока.
Верхняя ветвь отвечает такому состоянию потока, при котором с увеличением
глубины увеличивается и удельная энергия сечения (dЭ/dh>0). Состояние
потока, при котором его глубина больше критической (h>h
кр
), называется
спокойным состоянием потока. Примером спокойных потоков являются
равнинные реки, бурных –горные реки с большими продольными уклонами.
Продифференцировав (8.5) получим
dhg
dQ
1
dh
dЭ
3
2
ω
ωα
−=
(8.6)
Поскольку при критическом состоянии потока Э=Э(h) имеет минимум, то
dЭ/dh=0, поэтому
0
g
BQ
1
3
к
K
2
=
ω
α
− , откуда
g
Q
B
k
3
k
α
=
ω
(8.7)
Уравнение является основным уравнением критического состояния
потока, где
, B
k
ω
k
–площадь живого сечения и ширина потока при критическом
состоянии потока.

Уравнение (8.7) применяется для определения критической глубины при
заданном расходе воды и форме поперечного сечения потока. Задавшись
различными глубинами h и определив B, и ω
B
3
ω
, воспользуемся графиком
(рис 8.4).
h
g2
Q
2
α
К
h
В
3
ω
Рис.8.4. График критической глубины потока
Находим точку, абсцисса которой
g
Q
2
α
. Ордината этой точки и будет
критической глубиной.
В случае прямоугольного русла . Уравнение (8.7) принимает вид Bh=ω
g
Q
B
hB
2
k
3
k
3
k
α
=
. (8.8)
Введем параметр q=Q/B (расход на единицу ширины потока), тогда
g
q
h
2
k
α
= (8.9)
g
v
g
Q
B
h
2
k
2
2
k
л
к.ср
k
α
=
ω
α
=
ω
=
1F
gh
v
rk
к.ср
2
k
==
α
(8.10)
В спокойных потоках скорости меньше, чем в бурных потоках, а глубины
в спокойных потока больше, чем в бурных.
F
r
<F
rk
спокойное состояние потока;
→
F
r
>F
rk
бурное состояние потока.
→
Э
мин
=
g2
v
h
2
k
k
α
+
(уравнение при критическом состоянии потока).
Э
мин
=h
k
+h
ср.к
/2, α
kк.срh
h/h=
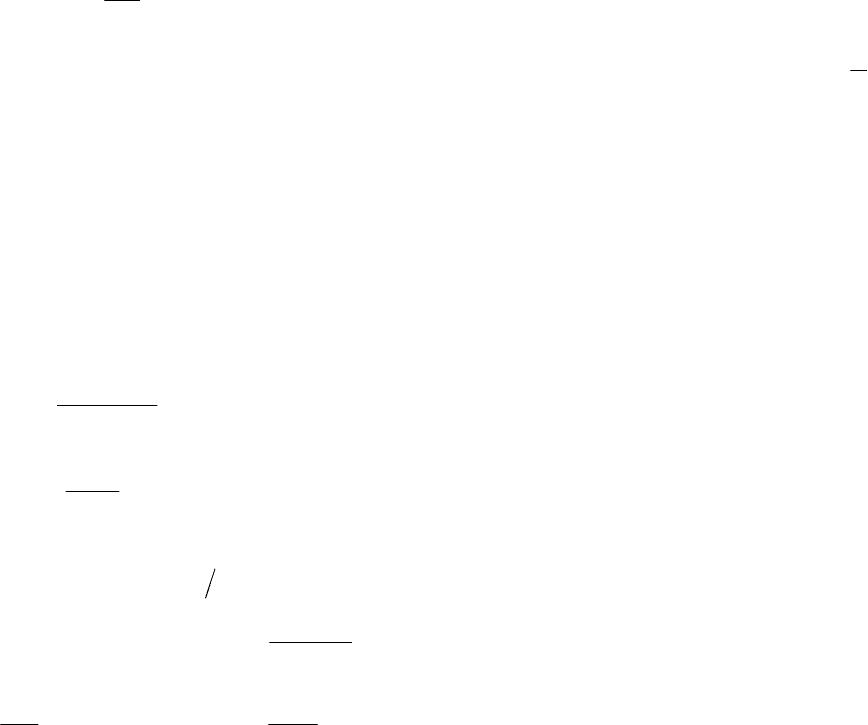
Э
мин
=(1+
k
h
h)
2
α
(8.11)
Для прямоугольного русла a
h
=1; Э
мин
=1,5h
k
, для параболического
7
2
h
=α
;
Э
мин
=1,33h
k
.
Уравнение (8.11) выражает линейную связь между удельной энергией
сечения и глубиной при критическом состоянии потока (F
rk
=1).
8.2.2. Критический уклон
Уклон призматического русла, при котором h
0
=h
k
называется
критическим уклоном.
Критический уклон можно определить по формуле
k
2
k
2
k
2
k
Rc
Q
I
ω
= (8.12)
α
ω
=
k
3
k
2
B
g
Q (8.13)
Подставляя выражение (8.13) в уравнение (8.12) и производя сокращение,
учитывая, что
kkk
R χω=
,
k
2
k
k
k
Bc
g
I
α
χ
= (8.14)
1
B
k
k
≈
χ
,
2
k
k
c
g
I
α
= (8.15)
I
0
<I
k
, то h
0
>h
k
–спокойное состояние потока.
I
0
>I
k
, то h
0
<hk –бурное состояние потока. При h≈ 0,025 и гидравлическом
радиусе R≈ 0,5…5,0 м, от которого зависит коэффициент Шези С,
I
k
≈ 0,0094…0,029.
8.2.3. Формы свободной поверхности потока при установившемся
неравномерном движении в призматических руслах
Как было отмечено ранее, существует 12 типов кривых свободной
поверхности. Их можно систематизировать в зависимости от соотношений
между нормальными и критическими глубинами, между уклоном дна и
критическим. Различают русла: с прямым уклоном (I
0
>0), горизонтальные (I
0
=0),
с обратным уклоном (I
0
<0).
При решении вопроса о формах кривых подпора и спада поток делится на
зоны. Зоной называется пространство, ограниченное линиями нормальных (0-0)
и критических (К-К) глубин или одной из них и линией дна.

h
0
N
N
a
1
K
b
1
K
C
B
h
k
J
o
<J
k
N
N
a
2
K
K
C
2
h
0
=
h
k
C
J
o
=J
k
Рис.8.5. Рис.8.6
Кривые свободной поверхности Кривые свободной поверхности
потока при h
0
>h
k
потока при h
0
=h
k
h
0
N
N
a
3
K
b
3
K
C
B
h
k
A
C
3
Рис.8.7.
Кривые свободной поверхности потока при h
0
<h
k
На рис. 8.5, 8.6 и 8.7 показаны потоки с прямым уклоном дна (отметка дна
снижается по течению). Формы свободной поверхности равномерного потока
являются предельным положением форм свободной поверхности
неравномерного потока. Линии нормальной глубины NN и линии критической
глубины KK называются гидравлическими осями. Они параллельно линии дна.
С помощью них четко выделяются возможные зоны расположения кривых
свободной поверхности при неравномерном движении.
Рассмотрим движение в призматических руслах, используя уравнение (8.4)
Нормальная глубина больше критической (h
0
>h
k
). Возможны три зоны
(см. рис 8.5).
В зоне А h>h
0
. Глубине h соответствует расходная характеристика К, а
глубине h
0
- характеристика К
0
. h>h
0
имеем К>К
0
, следовательно числитель в
правой части уравнения (8.4) больше нуля.
Число Fr<1 (спокойный поток), потому и знаменатель уравнения >0.
Получаем dh/dl>0,т.е. глубина потока увеличивается по течению.
При
, (Fr<1) числитель уравнения стремится к 0 и dh/dl>0,
следовательно в верхней части кривая свободной поверхности асимптотически
0
hh →
0
KK →
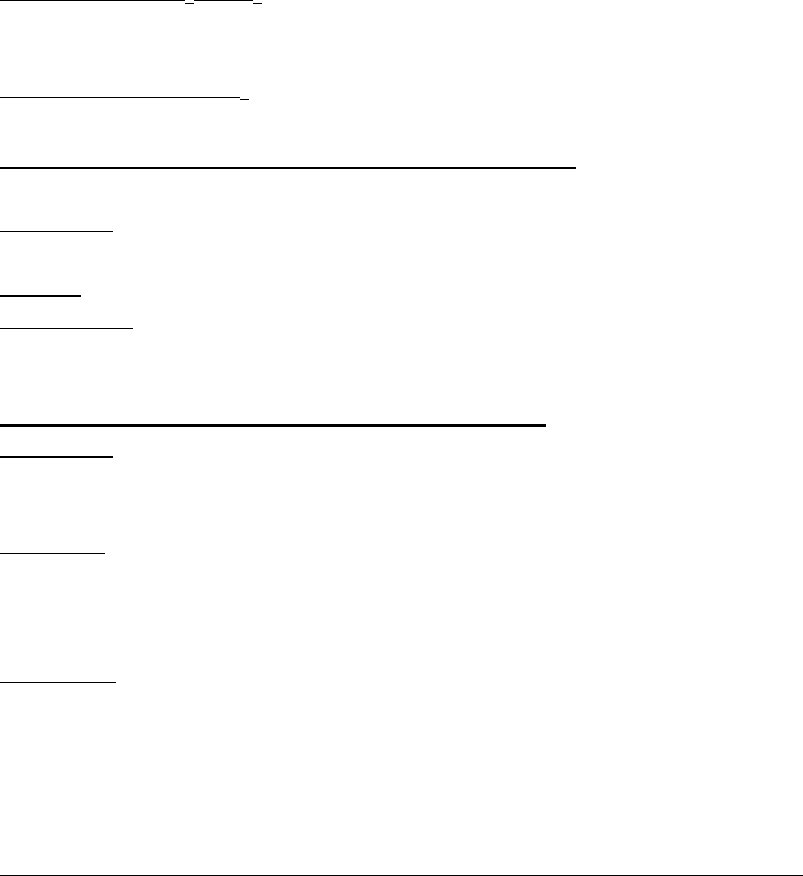
приближается к линии нормальных глубин NN. При , , , и
поэтому согласно (8.4) dh/dl
→
I
∞→h ∞→K
1
0Fr →
0
. Обращаясь к уравнению (8.4), видим, что в
этом случае уклон свободной поверхности I→ , т.е. в нижней части кривая
свободной поверхности асимптотически приближается к горизонтальной линии.
Итак, в зоне А имеем вогнутую кривую подпора
, поскольку она
асимптотически приближается в верхней части к линии NN, а в нижней –к
горизонтальной прямой. Эта форма свободной поверхности образуется перед
плотинами и мостами. Она чаще всего встречается на практике.
0
α
∞
h →
∞
В зоне B при h
0
>h>h
k
имеем выпуклую прямую спада b
1
. В верхней части
кривая асимптотически приближается к линии нормальных глубин. При
приближении h к h
k
кривая спада кончается водопадом (dh/dl
→
.
В зоне С при h<h
k
имеем вогнутую кривую подпора с
1
. При
получаем dh/dl
. Кривая заканчивается гидравлическим прыжком.
k
h
∞→
Нормальная глубина равна критической
(h
0
=h
k
) (см. рис. 8.6).
Возможны две зоны.
В зоне А
при h>h
0
имеем кривую подпора а
2
, близкую к горизонтальной
прямой. Эта кривая встречается при сопряжении водоемов с каналами I
0
=I
k
.
Зона В
отсутствует, т.к. h
0
=h
k
, т.е. гидравлические оси NN и КК совпадают.
В зоне С
при h<h
0
имеем кривую подпора c
2
, также близкую к
горизонтальной прямой. Эта кривая встречается при сопряжении каналов с I
0
>I
k
и I
0
=I
k
.
Нормальная глубина меньше критической
(h
0
<h
k
). См. рис. 8.7.
В зоне А
при h>h
k
имеем выпуклую кривую подпора а
3
, встречающуюся
перед преградой в бурном потоке. Эта кривая начинается гидравлическим
прыжком и имеет асимптоту в виде горизонтальной прямой.
В зоне В
при h
0
<h<h
k
имеем вогнутую кривую спада b
3
, встречающуюся на
быстротоках (водотоках при I
0
<I
k
) или при истечении воды из-под затвора в
водоток с большими уклонами. Вниз по течению кривая спада асимптотически
приближается к линии нормальных глубин.
В зоне С
при h<h
0
<h
k
имеем выпуклую кривую подпора с
3
. В нижней
части эта кривая подпора асимптотически приближается к линии нормальных
глубин.
Формы свободной поверхности неравномерного потока при I
0
<I
k
диаметрально противоположны формам потока при I
0
>I
k
, например, кривая а
1
вогнутая, а кривая а
3
выпуклая.
Потоки с горизонтальным дном и потоки с обратным уклоном дна.
Равномерное движение в таких потоках физически невозможно, так как,
например, при I
0
=0, исходя из уравнения (8.1), получим h
0
= (h
0
связано с
гидравлическим радиусом), т.е. гидравлическая ось NN должна быть
расположена в бесконечности.
Критическая глубина не зависит от уклона дна, а зависит только от
расхода воды и формы живого сечения, поэтому гидравлическая ось КК
сохраняет свое значение. Поэтому при I
0
=0 и I
0
<0 возможны две формы
свободной поверхности: выпуклая кривая спада, аналогичная b
1
, и вогнутая
кривая подпора, аналогичная с
1
(см. рис 8.5).

8.3. Построение кривых свободной поверхности в искусственных руслах
Существует много способов расчета кривых свободной поверхности [6].
Рассмотрим один из них. Для этого воспользуемся дифференциальным
уравнением установившегося неравномерного плавно изменяющегося
движения жидкости в призматических руслах. Призматические русла, как
правило, искусственные. Указанное уравнение имеет вид
Fr
K
K
I
dl
dh
−
−
=
1
1
2
2
0
0
, (8.16)
где I
0
– уклон дна потока, К
0
- расходная характеристика при равномерном
движении, К- расходная характеристика при неравномерном движении, Fr-
число Фруда.
Проинтегрируем уравнение (8.17) для случая прямого уклона русла (I
0
>0),
предварительно приведя его к виду удобного для интегрирования. Преобразуем
число Фруда Fr
ωω
α
ω
α
RC
RBC
g
KI
g
BQ
Fr
22
2
2
00
3
2
=== (8.17)
Учитывая, что
χ
ω
ω
==
R
RCK и
, уравнение (8.18) запишем
2
2
0
2
2
0
2
0
K
K
j
K
K
g
BCJ
Fr ==
χ
α
,
где j – параметр, включающий многие гидравлические элементы потока
χ
α
g
BCJ
j
2
0
= (8.18)
Если В=χ ⇒
g
CJ
j
2
0
α
=⇒ тогда с помощью параметра j учитывается
изменение удельной кинетической энергии потока на единице его длины.
С учетом (8.18) уравнение (8.16) принимает вид
2
0
2
2
0
2
0
1
1
K
K
j
K
K
I
dl
dh
−
−
=
или
j
K
K
K
K
I
dl
dh
−
−
=
2
0
2
2
0
2
0
1
, (8.19)
где К/К
0
- относительная расходная характеристика (при равномерном
движении воды равна единице).
Для интегрирования уравнения (8.20) Б.А. Бахметев предложил
использовать показательную функцию
x
h
h
K
K
=
0
2
0
2
, (8.20)
где
x
– гидравлический показатель русла, зависящий от формы русла и
показателя
y
в формуле для коэффициента Шези
y
R
n
C
1
= (
n
- к-т шероховатости русла,
y
-
переменный показатель, зависящий от
n
и
R
.
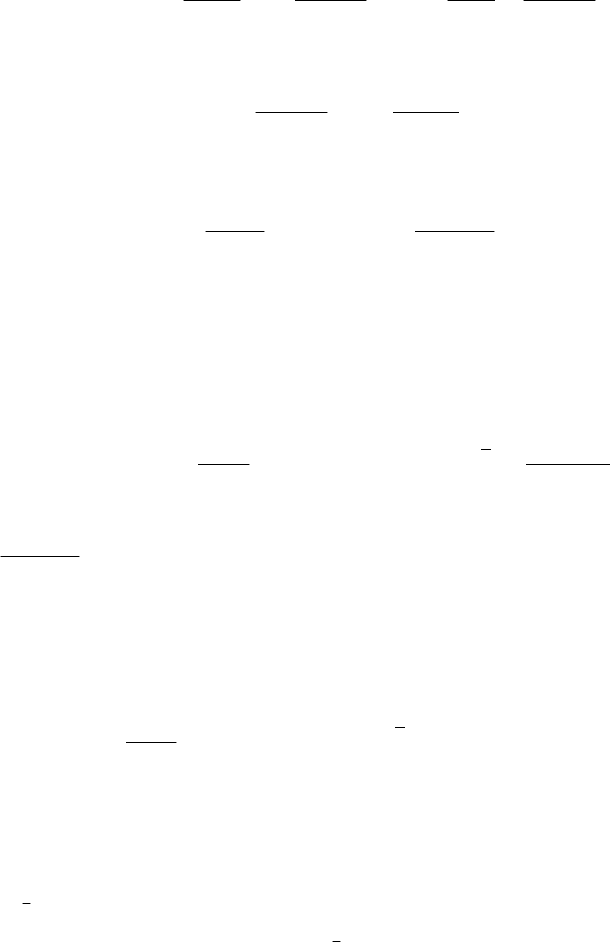
Зависимость (8.20) приближенная. Существует график К=f(h). Значения
гидравлического показателя русла для некоторых русел:
x
≈
3+2y (широкое прямоугольное);
x
≈
2 (узкое прямоугольное);
x
≈
4+2y (широкое параболическое);
x
≈
5+2y (треугольное);
x
≈
2,5+2y (гидравлически наивыгоднейшее, прямоугольное).
Значение показателя у определяется по формуле Павловского (см. ф. 4.67,
[1]).
Выведем уравнение неравномерного движения жидкости в
призматических руслах. Для этого проинтегрируем уравнения (8.19) и (8.20). В
уравнение (8.19) введем новую переменную, называемой относительной
глубиной
η
=h/h
0
.
Откуда dh=h
0
d
η
. После подстановки в уравнение (8.20)
j
I
dl
dh
x
x
−
−
=
η
η
η
1
0
0
или
η
η
η
d
j
h
dlI
x
x
1
0
0
−
−
= (8.21)
1
1
1
1 −
−
+=
−
−
xx
x
jj
ηη
η
.
Перепишем уравнение (8.21) в интегральной форме
∫∫∫
−
−
+=
2
1
2
1
1
1
0
0
0
η
η
η
η
η
η
η
d
j
d
h
dlI
x
L
, (8.22)
где η
1
=h
1
/ h
0
- относительная глубина выше по течению;
η
2
=h
2
/ h
0
- относительная глубина ниже по течению;
L – расстояние, между сечениями с глубинами h
1
и h
2
. Постоянную
I
0
/h
0
– вынесем за знак интеграла.
∫
−
−−−=
2
1
1
)1(
12
0
0
η
η
η
η
ηη
x
d
j
h
LI
(8.23)
⇒=
−
∫
)Б(
1
η
η
η
x
d
Функция Б(
η
) есть результат решения данного
интеграла, представленный в табличной форме.
Уравнение неравномерного движения жидкости в призматических
руслах, предложенное Б.А. Бахметевым
[
)Б()Б()1(
1212
0
0
ηηηη
−−−−=
j
h
LI
]
(8.24)
Значения Б(
η
) определяются в зависимости от безразмерной глубины
η
и гидравлического показателя русла x. Функции Б(
η
) вычислены путем
разложения подинтегральной функции в ряд при различных значениях
η
и x.
Параметр
j вычисляют по формуле
)(5,0
21
jjj
+=
,
