Лекции - Уравнения движения жидкости Л. Эйлера
Подождите немного. Документ загружается.

Г л а в а 4
Уравнения движения жидкости Л. Эйлера
В соответствии с основным – вторым законом динамики И.Ньютона
произведение массы m на ускорение dw/dt равно сумме внешних
действующих сил F:
m dw/dt = F. (4.1)
Л. Эйлер предложил формы этого закона, удобные для исследования
движущейся жидкости.
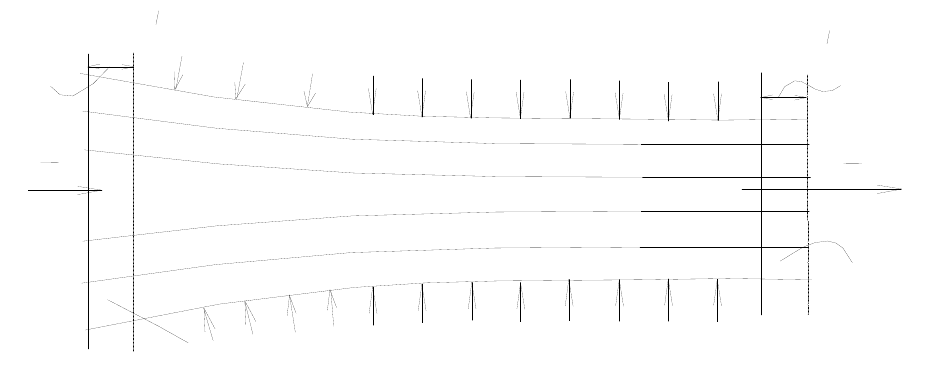
4.1 Уравнение количества движения для струйки тока
Наиболее простая из этих форм – гидравлическая, применима для
стационарного течения несжимаемой жидкости на участке (АB) трубки тока,
рисунок 4.1.
A
B
d m
P
f
B
A
P
P
d m
2
f
w
1
1
1
w
2
2
d t
w
2
w
1
d t
m
Рисунок 4.1 - К вопросу об изменении количества движения на участке трубки тока
стационарно движущейся несжимаемой жидкости
29
На массу m жидкости на участке АB трубки тока действуют внешние
(поверхностные и объемные) силы F, изменяя скорость на участке АB на
величину w = w
2
– w
1.
Но это изменение скорости фактически распределяется
на часть массы жидкости dm, которая войдет и выйдет за время dt через
сечения f
1
и f
2
со скоростями w
1
и w
2
соответственно. Из условия
сохранения массы для несжимаемой жидкости следует
dm = w
1
f
1
dt = w
2
f
2
dt = Qdt.
При этом количество движения остальной части жидкости (на участке A
1
– B)
не изменяется . В этом смысле можно сказать, что изменение скорости w на
участке АB под действием сил F получает за время dt только часть
жидкости dm. Поэтому второй закон Ньютона в данном случае можно записать
в виде
dm w/dt = Qdt w/dt = F.
Подставляя w = w
2
– w
1
, получим (после сокращения на dt):
Q(w
2
– w
1
) = F. (4.2)
Это и есть уравнение количества движения для струйки тока
(Л.Эйлер, 1757).
Отметим, что ускорение при установившемся движении в данном случае
возникает как бы в результате переноса за время dt массы dm жидкости из
начального сечения А, где скорость w
1,
в конечное B, где скорость w
2
. Такое
ускорение жидкости называют конвективным (в отличие от локального w/t,
возникающего в данной точке пространства только при неустановившемся
течении).
30
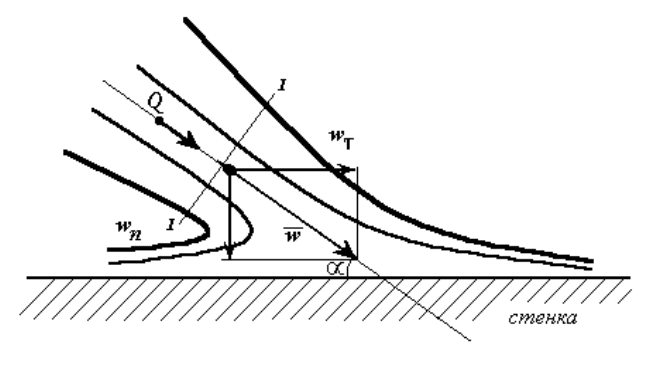
4.2 Примеры использования уравнения количества движения
4.2.1 Сила давления R струи на плоскую стенку, расположенную под
углом к оси струи
Выберем сечения потока как показано на рисунке 4.2. Спроектируем
уравнение количества движения (4.2) на касательное () и нормальное (n)
направления к поверхности
Q(w
1
– w
2
) = F
,
Q(w
1
n
– w
2
n
) = F
n
.
Рисунок 4.2. Схема натекания струи на плоскую стенку под углом .
Если жидкость невязкая, касательные напряжения раны нулю, и сила в
этом направлении отсутствует: F
= 0.
В направлении нормали сила воздействия стенки на струю F
n
очевидно
равна по величине и противоположна по направлению силе давления струи на
стенку
R = – F
n
= – Q (w
1
n
– w
2
n
) = Q (w
1
n
– 0) =
= Q w
1
sin = f
1
w
1
2
sin, (4.3)
где f
1
– площадь сечения струи.
31
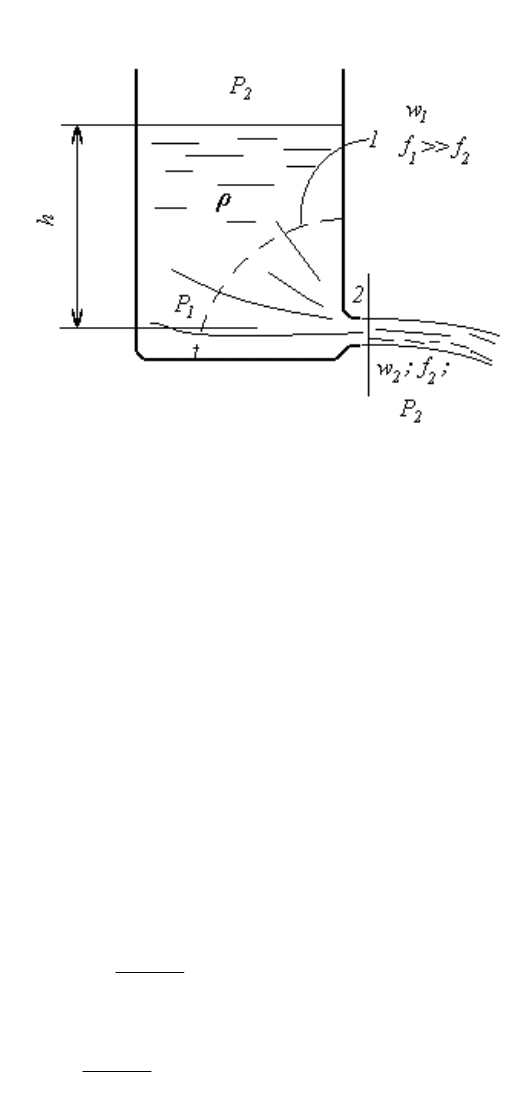
4.2.2 Реакция вытекающей струи
Истечение струи жидкости плотностью из бака (см. рисунок 4.3)
происходит под действием перепада давлений
p = p
1
– p
2
= gh,
где h - глубина расположения насадка (отверстия).
Рисунок 4.3. Истечение тяжелой (капельной) жидкости из бака.
В баке на значительном расстоянии перед отверстием в сечении f
1
жидкость можно считать неподвижной (w
1
0). Уравнение (4.2) принимает
вид
F = Qw
2
. (4.2
11
)
Величину p = gh можно рассматривать как потенциальную энергию
единицы объема жидкости, которая в сечении f
2
переходит (без потерь) в
кинетическую энергию
w
2
2
, т.е.
p = gh =
w
2
2
,
откуда
32
w
2
=
2 p
=
2gh
=
Q
f
2
.
Поскольку сумма сил F, действующих на струю, сонаправлена вектору
w
2
, то уравновешивающая сила ее сила реакции R (действующая на стенки
бака и насадки) направлена в противоположную сторону:
R = – F = – Qw
2
.
Таким образом, реакция R противоположна скорости течения w
2
, равна
удвоенной величине силы статического давления на площадь f
2
сечения струи
R = Qw
2
= Q
2gh
= 2gf
2
h= 2pf
2
. (4.4)
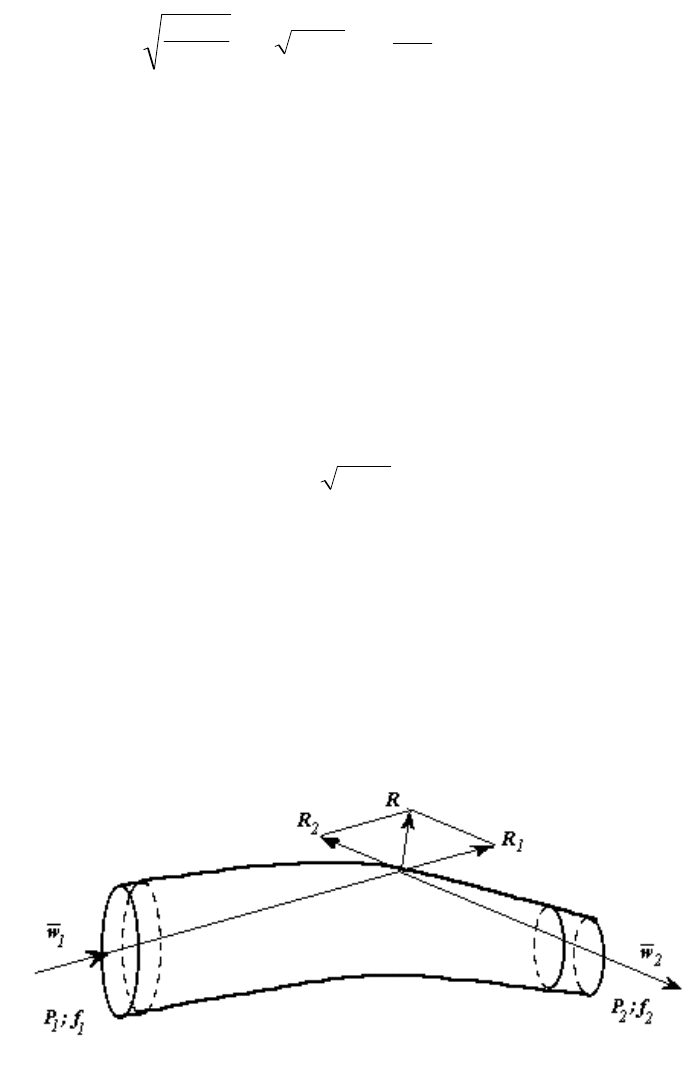
4.2.3 Давление потока на криволинейные стенки канала
При движении по криволинейному каналу жидкости на его стенки
действуют силы давления (см. рисунок 4.4), а на торцевые(живые) сечения f
1
и
f
2
и сила инерции потока, определяемая по уравнению количества движения.
Рисунок 4.4- Схема сил, действующих на стенки канала со стороны жидкости
Во входном сечении f
1
действует сила R
1
, динамическая составляющая
которой равна секундному количеству движения f
1
w
1
2
, а статическая – силе
гидростатического давления p
1
f
1
, так что
R
1
= p
1
f
1
+ f
1
w
1
2
.
Аналогично в сечении f
2
:
33
R
2
= p
2
f
2
+ f
2
w
2
2
.
Полная сила R воздействия потока на стенки канала равна
геометрической сумме сил R
1
и R
2
направленных по внутренним нормалям к
сечениям f
1
и f
1
), см. рисунок 4.4:
R = R
1
+ R
2 .
(4.5)
Полученные соотношения лежат в основе прикладных расчетов силового
воздействия потока на стенки каналов гидромашин.
4.3 Уравнение момента количества движения для исследования
вращательного движения жидкости также предложено Л.Эйлером.
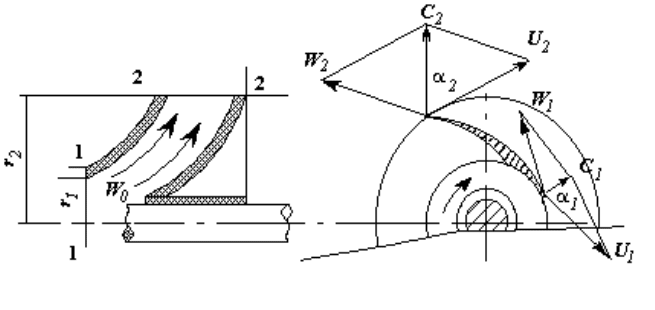
Рассмотрим движение жидкости в рабочем колесе центробежного насоса,
рисунок 4.5.
Рисунок 4.5 - Схема движения жидкости в рабочем колесе ценробежного насоса
Пусть r
1
и r
2
– внутренний и внешний радиусы, u
1
= r
1
, u
2
= r
2
соответствующие окружные скорости колеса, имеющего угловую скорость .
Абсолютная скорость жидкости на входе и выходе межлопаточного
канала c
1
и c
2
. Скорость w
движущейся частицы жидкости массой m
относительно колеса равна векторной разности соответствующих абсолютных
c
и окружных u
скоростей
w
i
= c
i
– u
i
(i = 1,2)
34

Если
i
– угол между векторами c
i
и u
i
(u
i
всегда направлена по
касательной), то момент количества движения относительно оси вращения
колеса
m
i
c
i
r
i
cos
i
Применяя теорему об изменении количества движения (второй закон
Ньютона для вращательного движения) – "изменение (во времени) момента
количества движения относительно оси вращения равно моменту внешних сил
M":
(mcrcos )
t
= M,
или
m(c r c r
t
2 2 1 1
cos cos )
2 1
=M.
(4.6)
Это и есть уравнение Эйлера.
Замечая, что
m
t
= Q [кг/c] – секундный массовый расход жидкости,
последнее уравнение можно переписать в виде (после умножения обеих частей
на угловую скорость ):
Q (с
2
r
2
cos
2
– c
1
r
1
cos
1
) = P, (4.7)
где P = M – мощность.
Полученное уравнение (4.7) используется для расчета лопастных
роторных машин - насосов, турбин (для турбин векторы с
2
и с
1
имеют
противоположные направления, т.к. поток входит в сечение "2", а выходит из
сечения "1").
Мощность будет максимальной при cos
1
= 0 (радиальный вход потока
для насоса и радиальный выход для турбины). В этом случае:
P = P
max
= Q с
2
u
2
cos
2
.
(4.7
1
)
35
4.4 Уравнение движения жидкости Эйлера в частных произведениях
Это уравнение описывает наиболее общий случай (установившегося и
неустановившегося) движения идеальной (сжимаемой и несжимаемой)
жидкости. Его можно получить, если, в соответствии со вторым законом
Ньютона (4.1), сумму всех действующих на частицу жидкости сил, отнесенных
к единице массы F/m, приравнять ее ускорению dw/dt. Но величина уже
подсчитана при выводе дифференциальных уравнений гидростатики Эйлера:
(R –
1
p) - для объемных и поверхностных сил давления. Поэтому
эти уравнения легко обобщаются на искомые уравнения, описывающие
движущуюся идеальную жидкость:
dw/dt = R –
1
p (4.8)
– в векторной записи;
d
w
d t
X
= R
x
–
1
p
x
;
d
w
dt
y
= R
y
–
1
p
y
; (4.8
1
)
d
w
dt
Z
= R
z
–
1
p
z
;
– в проекции на оси координат;
d
w
dt
i
= R
z
–
1
p
x
i
, i = 1,2,3 (4.8
11
)
– в тензорных обозначениях.
В этих уравнениях Л. Эйлера w(x,y,z) – скорость жидкой частицы,
координаты которой сами изменяются во времени: x(t); y(t); z(t). Поэтому
входящие в уравнение (4.8) полные производные по времени для каждой из
проекций скорости можно записать в виде
36

d
w
dt
=
w
t
+
w
dx
x dt
+
dy
y dt
+
w
z dt
=
X X X X X
W
dz
=
w
t
+
w
w
x
+
w
w
y
+
w
w
z
X
X
X
y
X
Z
X
, (4.9)
где
dx
dt
= w
x
;
dy
dt
= w
y
;
dz
dt
= w
z
.
Или более кратко: в тензорных обозначениях:
d
w
dt
w
t
+
w
w
x
K
K
i i i
=
, (4.9
1
)
где i = 1; 2; 3; ( по немому индексу "к" предполагается суммирование) к =
1,2,3.
В векторных обозначениях:
dw/dt =
w/
t + (w)w. (4.9
11
)
Здесь первые слагаемые – частные произведения по времени от скорости
w/
t показывают изменение скорости w во времени в данной точке
пространства (локальные ускорения), а остальные слагаемые (w)w отражают
изменение скорости w при перемещении частицы из одной точки пространства
в другую (конвективное ускорение).
Таким образом, уравнения Эйлера можно записать в развернутом виде в
проекциях на оси координат
w
t
+
w
w
x
+
w
w
y
+
w
w
z
X
X
X
y
X
Z
X
= R
x
–
1
p
x
;
w
t
+
w
w
x
+
w
w
y
+
w
w
z
y
X
y
Z
y
y
y
= R
y
–
1
p
y
; (4.10)
w
t
+
w
w
x
+
w
w
y
+
w
w
z
Z
X
Z
y
Z
Z
Z
= R
z
–
1
p
z
;
в векторном виде:
w/
t + (w)w = R –
1
gradp (4.10
1
)
37
в тензорных обозначениях
w
t
+
w
w
x
K
K
i i
= R
i
= –
1
p
x
i
, (i = 1,2,3; (4.10
11
)
k = 1,2,3)
Дифференциальные уравнения Эйлера совместно с уравнением
неразрывности для несжимаемой жидкости ( = const) жидкости (3.11)
образуют систему четырех уравнений, содержащих четыре неизвестных w
x
; w
y
;
w
z
; p.
В случае сжимаемой ( const (p)) жидкости (газа) к уравнениям
Эйлера и неразрывности (3.12) необходимо добавить еще одно, определяющее
связь между давлением и плотностью
= f(p), (4.11)
где f(p) – заданная функция.
Это уравнение называется условием баротропности и, являясь
предположением*
)
, во многих случаях хорошо оправдывается опытом.
Интегрируя эти замкнутые системы уравнений (для несжимаемой или
сжимаемой жидкостей) при заданных граничных и начальных (для
неустановившихся течений) условиях, можно в принципе определить вектор
скорости и давление (а для сжимаемой жидкости и плотность) в любой точке
потока и в любой момент времени.
Обычно выделяют два рода задач: внешние и внутренние задачи. К
внешним относятся задачи обтекания тел, находящихся в потоке (например,
обтекание крылового профиля): к внутренним - исследование течений внутри
проточных систем (течение в трубе).
Граничные условия при обтекании тел задают распределение скоростей и
давлений вдали от тела. Поскольку внешние задачи обычно рассматриваются в
системе координат, связанных с обтекаемым телом, задаются:
38
