Лекции - Уравнение баланса энергии
Подождите немного. Документ загружается.

Г л а в а 5
Уравнение баланса энергии
Уравнения Эйлера в частных произведениях допускают аналитические
решения при исследовании течений жидкости лишь в немногих случаях. С
практической точки зрения наиболее важным является интеграл этих уравнений
для стационарного течения, выражающий баланс энергии жидкости (или газа)
вдоль линии тока – уравнение Бернулли.
Если из внешних массовых сил действует лишь сила тяжести, а ось z
направлена вертикально вверх.(R
z
= – g), уравнения Эйлера примут вид:
d
w
dt
X
= –
1
p
x
;
d
w
dt
y
= –
1
p
y
;
d
w
dt
Z
= –
1
p
z
– g.
Проинтегрируем эту систему вдоль некоторой линии тока. Для этого
умножим каждое из уравнений соответственно на dx, dy, dz и сложим
d
w
dt
X
dx +
d
w
dt
y
dy +
d
w
dt
Z
dz = –
1
(
p
x
dx +
p
y
dy +
+
p
z
dz) – gz. (5.1)
Замечая, что
d
w
dt
X
dx = dw
x
dx
dt
= w
x
dw
x
= d (
X
2
w
2
),
и, аналогично,
d
w
dt
y
dy = d (
d
w
2
y
2
);
d
w
dt
Z
dz = d (
Z
2
w
2
),
левую часть уравнения можно записать так
40
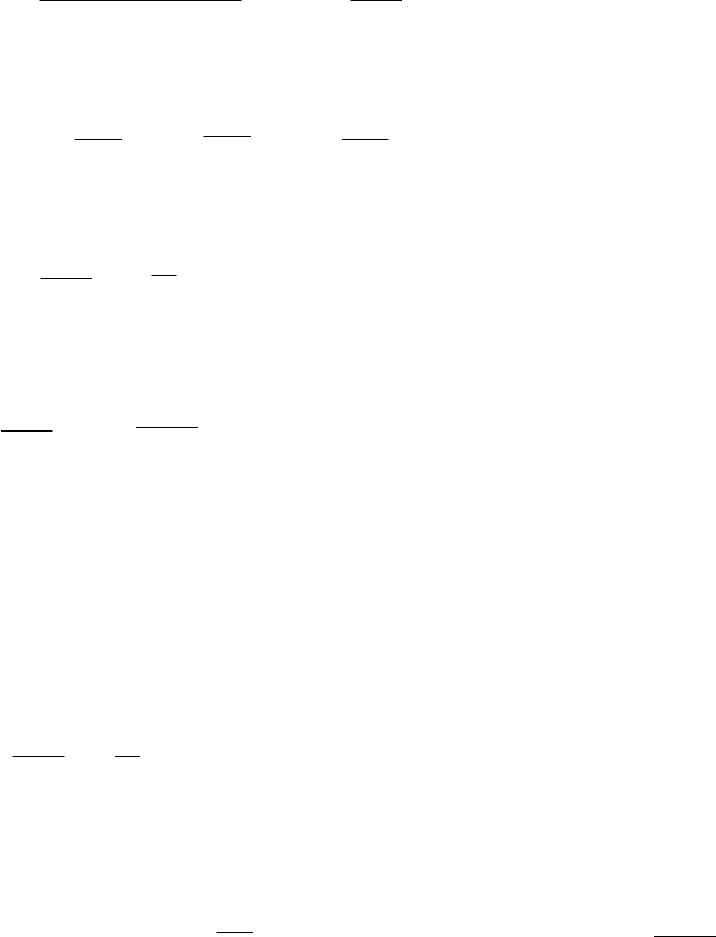
d (
X
2
y
2
Z
2
w
+
w
+
w
2
) = d (
2
w
2
),
а в правую ввести полный дифференциал давления
dp =
p
x
dx +
p
y
dy +
p
z
dz.
Тогда уравнение (5.1) примет вид:
d (
2
w
2
) +
1
dp + gdz = 0, (5.1
1
)
или, после интегрирования
2
w
2
+
dp
(p)
+ gz = const. (5.2)
Последнее выражение называется уравнением Бернулли. Рассмотрим
случаи несжимаемой жидкости и газа.
Для несжимаемой жидкости = const, так что последнее уравнение
после деления на g примет вид:
2
w
2g
+
p
+ z = const = H, [м] (5.2
1
)
где = g – удельный вес, а H – полный напор (постоянная интегрирования);
z – геометрическая,
p
– пьезометрическая высоты;
w
g
2
2
– скоростной
напор.
Уравнение (5.2) выражает условие сохранения энергии (единицы веса)
несжимаемой жидкости вдоль линии тока.
41
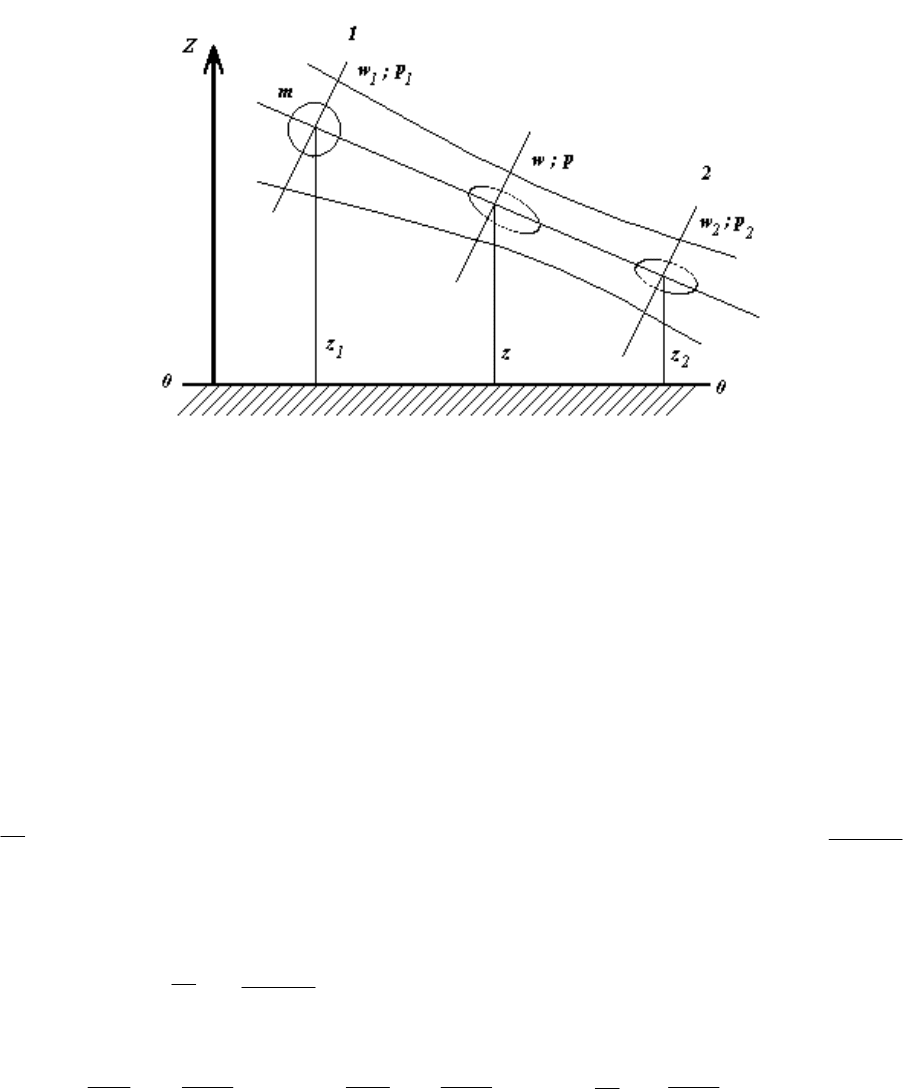
Рисунок 5.1 К выводу уравнения Бернулли.
Это уравнение можно получить, рассматривая энергию жидкой частицы
массой m, движущеюся вдоль линии тока (см. рисунок 5.1).
Полная потенциальная энергия частицы характеризуется энергией
положения mgz относительно исходного уровня 0 – 0 и энергией давления
mg
p
. Полная механическая энергия, включающая еще кинетическую
m
w
2
2
,
должна сохраняться вдоль линии тока, т. е.:
mgz + mg
p
+
m
w
2
2
= const, или, деля на mg:
z
1
+
1
p
+
1
2
w
2q
= z
2
+
2
p
+
2
2
w
2q
= z +
p
+
2
w
2q
= H = const.
Благодаря линейной размерности слагаемых, это уравнение допускает
наглядное геометрическое толкование. Представим, что в контрольных
сечениях
трубки тока подключены прозрачные манометрические трубки. См. рисунок
5.2, где обозначено:
z
i
– высота геометрического центра тяжести i – го сечения над плоскостью
42
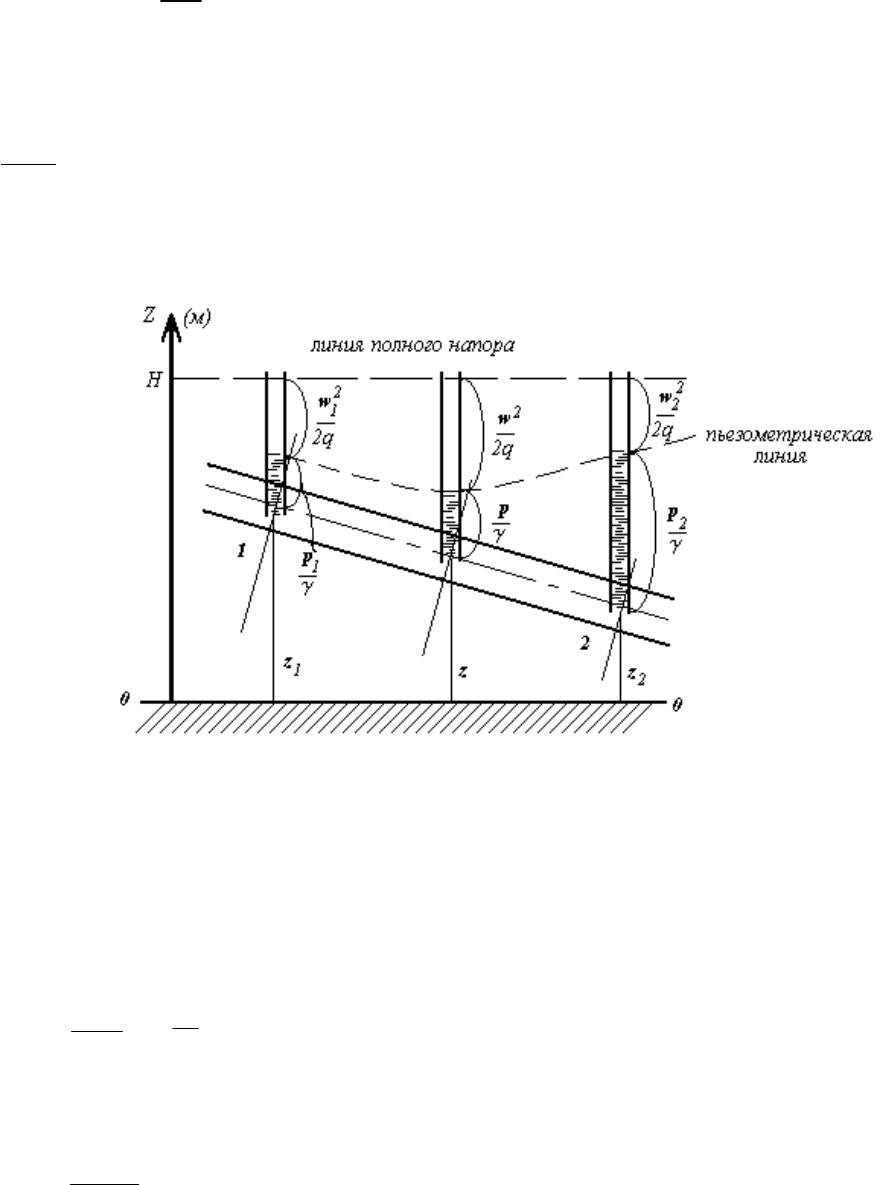
0 – 0;
i
p
– пьезометрическая высота столба жидкости в
манометрической трубке;
i
2
w
2g
– скоростная высота(напор); H – полный напор.
Рисунок 5.2 - Изменение полного напора и его составляющих вдоль линии
тока для идеальной жидкости
Умножая уравнения (5.2
1
) на g и на , получим еще две разновидности
уравнения Бернулли:
2
w
2
+
p
+ gz = const, [м
2
/c
2
] – (5.2
11
)
– для энергии единицы массы жидкости;
w
2
2
+ p + z = const, [Па] – (5.2
111
)
– для энергии единицы объема жидкости.
43
Связывая параметры w, p, z, H для различных сечений потока, уравнение
Бернулли (5.2
1
); а также в формах (5.2
11
); (5.2
111
) позволяет решать множество
задач гидравлики.
Для сжимаемого газа из -за малой плотности силу тяжести можно не
учитывать, так что уравнение (5.2
1
) упростится:
2
w
2
+
dp
(p)
= const; (5.2
1111
)
При этом обычно принимается, что зависимость (p) соответствует адиабате:
p
=
p
K
0
K
0
= const. (5.3)
Здесь к = c
p
/cv – показатель адиабаты, равный отношению изобарной и
изохорной теплоемкостей газа; а индекс "0" означает, что параметры относятся
к адиабатически заторможенному газу (при весьма малой скорости газа), когда
w
2
0, давление и плотность его принимают значения p
o
и
o
. Интегрируя
(5.2
1111
) при условии (5.3), получим
2
w
2
+
k
k - 1
p
=
k
k - 1
o
o
p
(5.4)
Это уравнение Бернулли-Сен-Венана (1839) выражает условие
сохранения энергии вдоль линии тока для совершенного (термодинамически
идеального) газа. Оно играет ту же роль в прикладной газодинамике
одномерных течений, что и уравнение (5.2) в гидравлике несжимаемой
жидкости.
Используя уравнение состояния идеального газа
p
= RT,
уравнение (5.4) можно записать так
2
w
2
+
k
k - 1
RT =
k
k - 1
RT
o
, (5.4
1
)
44

где T и T
o
— абсолютные температуры движущегося (со скоростью w) и
заторможенного (покоящегося) газа соответственно.
Учитывая, что
k
k - 1
R =
p v
p v
p v
c c
c c
- 1
(
c
-
c
/
/
)
= с
p
,
а c
p
T = h – энтальпия (теплосодержание) газа, уравнение (5.4
1
) можно
записать и так:
2
w
2
+ h = h
o
(5.4
11
)
Это наиболее легко запоминающаяся форма уравнения Бернули-Сан-
Венана.
Сравнивая (5.4) и (5.2
1
), видно, что (кроме отсутствия гравитационной
составляющей gz) отличие состоит в множителе
k
k - 1
при пьезометрической
составляющей, которая, например, для воздуха
k
k - 1
=
1 4
1 4 1
,
, -
3,5. Это
связано с тем, что в энтальпию h газа входит и его внутренняя энергия u,
которая в случае сжимаемого газа является переменной величиной:
k
k - 1
p
= h = u +
p
.
45
