Лекции - Скачки уплотнения
Подождите немного. Документ загружается.

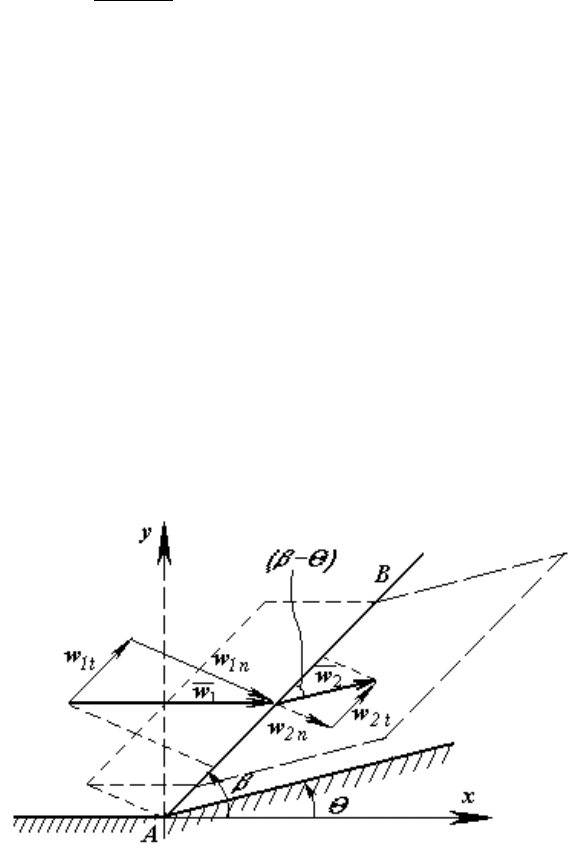
утверждающее. что при прохождении газа сквозь косой скачок уплотнения
касательная составляющая скорости сохраняется; скачкообразно изменяется
лишь нормальная составляющая.
С учетом этого свойства, перепишем последнее уравнение (п.(г)) в виде:
h
1
+ w
2
1
n
/2 = h
2
+ w
2
2
n
/2
и, сравнивая его, а также равенства п.п. а) и б) с соответствующими
уравнениями (10.12) , (10.13), (10.14) для прямого скачка, убедимся, что три
основных равенства для косого скачка
1
w
1n
=
2
w
2n
;
p
1
+
1
w
2
1n
= p
2
+
2
w
2
2n
;
h
1
+ w
2
1
n
/2 = h
2
+ w
2
2
n
/2
полностью совпадают с соответствующими уравнениями теории прямого
скачка, если под скоростью до и после скачка подразумевать нормальную ее
составляющую. Это освобождает нас от повторения сделанных выше выводов
формул: можно утверждать, что соотношения между давлениями и
плотностями, устанавливаемые адиабатой Гюганио (10.5) справедливо и для
косого скачка.
Рисунок 10.5 - Контрольная поверхность при переходе через косой скачок АВ
Остаются теми же, что и в случае прямого скачка, основанные на законе
сохранения энтальпии торможения h
o
равенства:
11
h
1o
= h
2o
= h
o
; T
1o
= T
2o
=T
o
; a
1o
= a
2o
= a
o
, (10.18)
а, следовательно, и
Т
1кр
= Т
2кр
= Т
кр
; а
1кр
= а
2кр
= а
кр
= w
кр
. (10.19)
Для нормальных компонент скоростей сохраняется и формула Прандтля
(10.11) с несколько измененной правой частью. Разница связана с тем, что в
уравнение энергии в форме
2
2
w
2
+
k
=
k + 1
2(k - 1)
w
kp
2
1
a
-
,
с учетом того, что w
2
= w
2
t
+ w
2
n
, можно представить в виде:
n
kp
t
kp
2
2
2
2
w
2
+
k - 1
=
k + 1
2(k - 1)
w
-
w
2
=
k + 1
2(k - 1)
w
2
a
~
,
где
kp kp
t
2
2 2
w
=
w
-
k - 1
k + 1
w
~
(10.20)
"приведенная" критическая скорость, также сохраняющаяся при прохождении
скачка. В соответствии с этим, уравнения Прандтля для косого скачка примут
вид:
w
1n
w
2n
=
kp
2
w
~
или
1n 2n
~ ~
= 1, (10.11
1
)
где
n
n
kp
=
w
w
i
i
~
~
. (10.21)
Обращаясь к скоростным треугольникам на рисунке 10.5, приходим к
зависимостям для косых скачков:
12
w w w w
w w w w
n n
t t t
1 1 2 2
1 1 2
sin ; sin ;
cos cos
-
(10. 22)
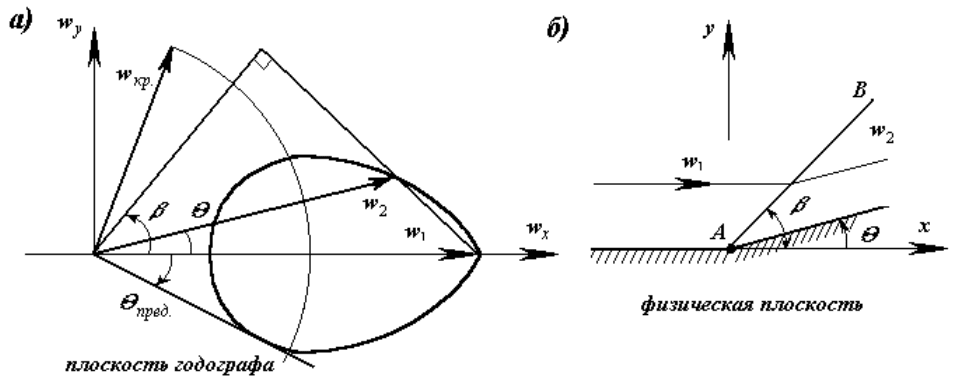
10.5 Ударная поляра. Отсоединенный скачок уплотнения
Если в плоскости годографа скорости [w
x
;w
y
] (рисунок 10.6) отложить
из начала координат вектора скоростей до и после скачка, в соответствии с
рисунком 10. 5, то конец вектора w
2
будет лежать на кривой, которая проходит
из вершины вектора w
1
, образуя петлю, и называется ударной полярой*
)
(для
каждого значения w
1
существует соответствующая ударная поляра). Зная w
1
и,
например , графически легко определяются углы и w
2
.
Рисунок 10.6 -Ударная поляра (а); картина течения (б)
13
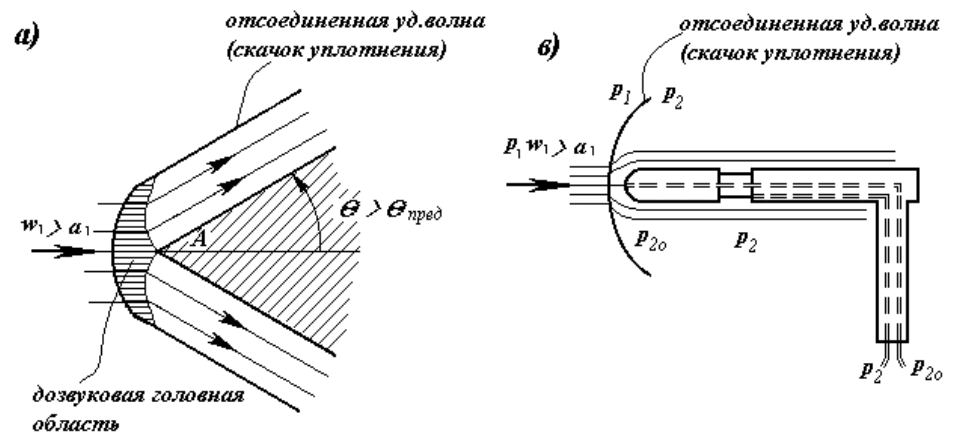
Значение <
пред
соответствует углам отклонения потока, при которых
косой скачок может существовать. Если >
пред
, возмущение сжатия
слишком велико; возникает отсоединенный скачок уплотнения (отсоединенная
или головная ударная волна), рисунок 10.7.
Рисунок 10.7 - Отсоединенный скачок уплотнения:
а) - перед клином; б) - перед трубкой Приндтля
_______________________________
*
)
Кривые этого семейства математически представляют собой строфонды (их еще
называют гипоциссоидами или декартовыми листами).
В головной ударной волне контрольная часть являет собой прямой
скачок, за которым располагается дозвуковая область; а по краям - косые
скачки.
Чем выше w
1
, тем больше
пред
, но даже для М
1
=
пред
< 46
0
. Как и в
прямых, в косых скачках энтропия возрастает. Коэффициент восстановления
давления убывает с ростом М
1
sin вплоть до = 90
0
(прямой скачок).
Для уменьшения потерь в сверхзвуковых потоках стремятся не допускать
прямых скачков, заменяя их косыми: носовую часть обтекаемых тел заостряют
(рис.10.8).
Конические скачки (трехмерные) возникают при продольном обтекании
конуса (иглы). Их интенсивность меньше, чем косых при плоских течениях
(рисунки 10.8 и 10.9).
14
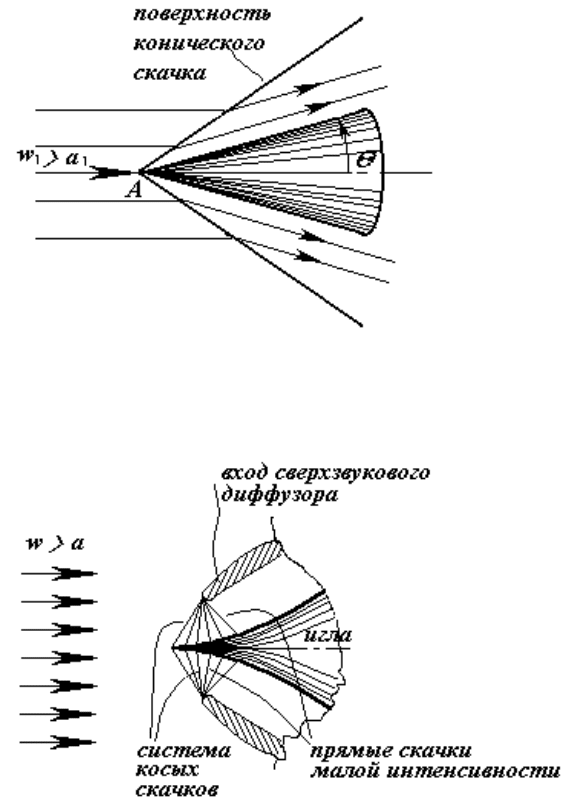
Рисунок 10.8 - Обтекание конуса (иглы) сверхзвуковым потоком
Рисунок 10. 9 - Вход в камеру реактивного двигателя с "иглой", разбивающей
головную ударную волну на систему конических скачков
10.6 Взаимодействие сверхзвукового потока с ограничивающими
поверхностями
10.6.1 Силы, действующие на обтекаемое тело со стороны сверзвукового
потока
Картина обтекания тонкой пластинки сверзвуковым потоком
представлена на рисунке 10.10.
15
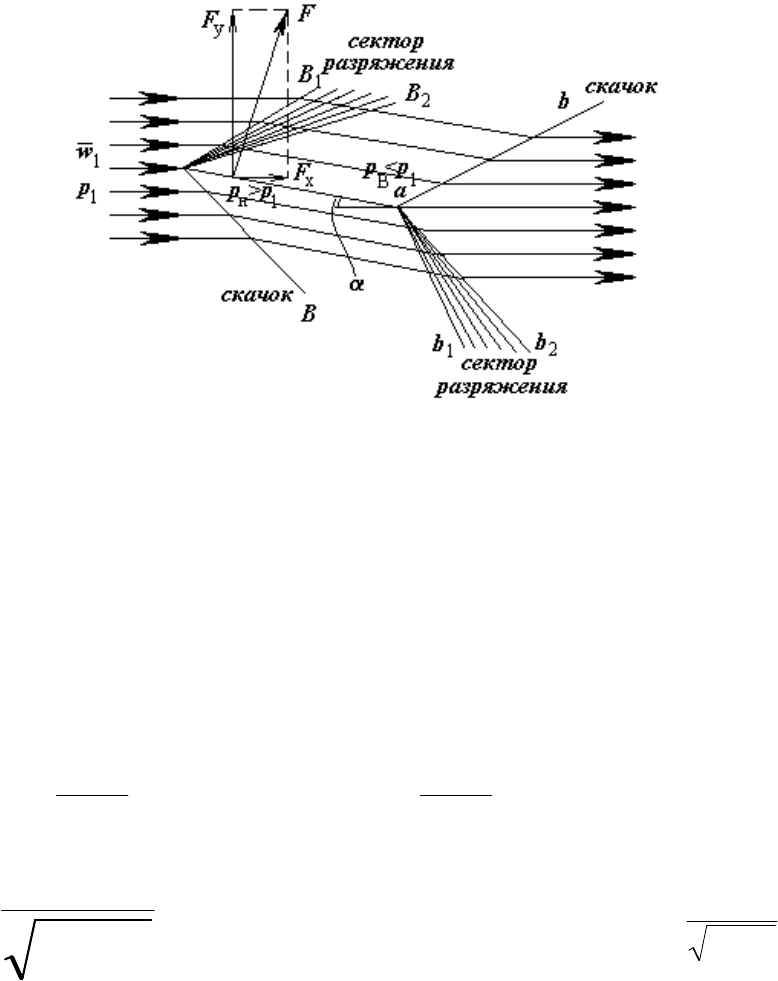
Рисунок 10.10 - Обтекание плоской пластины сверхзвуковым потоком, установленной
под углом атаки к набегающему потоку
Равнодействующая F аэродинамических сил, перпендикулярная
плоскости пластины. может быть разложена на горизонтальную F
x
(силу
сопротивления) и вертикальную F
y
(подъемную силу).
Если > 0 (угол атаки - между пластиной и w
1
), то
F
y
= C
y
f
1
1
w
2
2
; F
x
= C
x
f
1
1
w
2
2
, (10.23)
где C
y
=
4
M
1
2
1
; C
x
=
4
M
2
2
1
- 1
;*
)
(10.24)
_________________________________
*
)
Эти формулы дают значительные ошибки при М 1, а также при увеличении
толщины пластины и ее изгибах; С
y
и С
x
- коэффициенты подъемной силы и силы
сопротивления соответственно.
f - площадь пластины;
М
1
= w
1
/a
1 .
Потери энергии потока в скачках уплотнения называются волновыми
потерями (F
x
- волновое сопротивление).
16
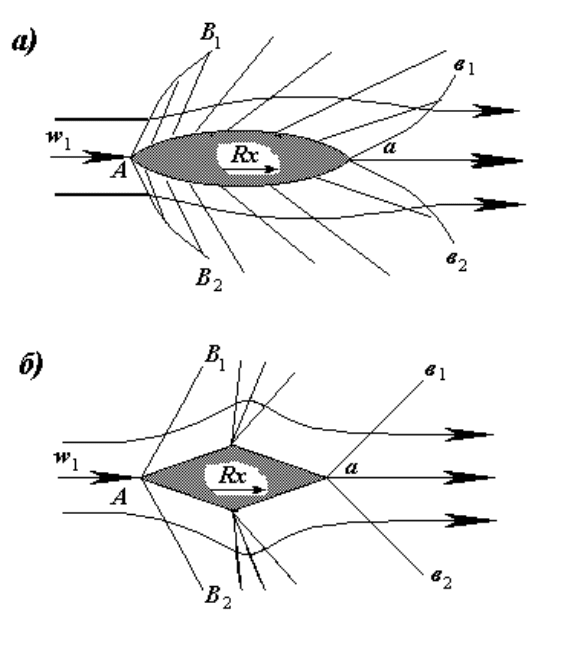
При сверхзвуковом обтекании тел с заостренной передней кромкой, поле
течений всегда включает в себя косые скачки и волны разрежения (рисунок
10.11 а, б).
При плавных очертаниях волны разрежения распределяются равномерно;
при ломаных - фокусируются в вершинах изломов (см. рисунок 10.11). Если
= 0 (симметричное обтекание). то F
y
= 0.
Рисунок 10.11 - Обтекание чечевицеобразного (а) и ромбовидного (б) крыльев
У тонких профилей силы можно оценивать по формулам для пластинки
(10.23), (10.24), для толстых профилей необходимо учитывать форму
поверхности.
Затупление носовой части увеличивает волновое сопротивление, обычно
приводит к отсоединенной ударной волне (см. выше).
Отражение волн давления от твердой стенки и свободной границы струи
газа всегда имеет место.
17
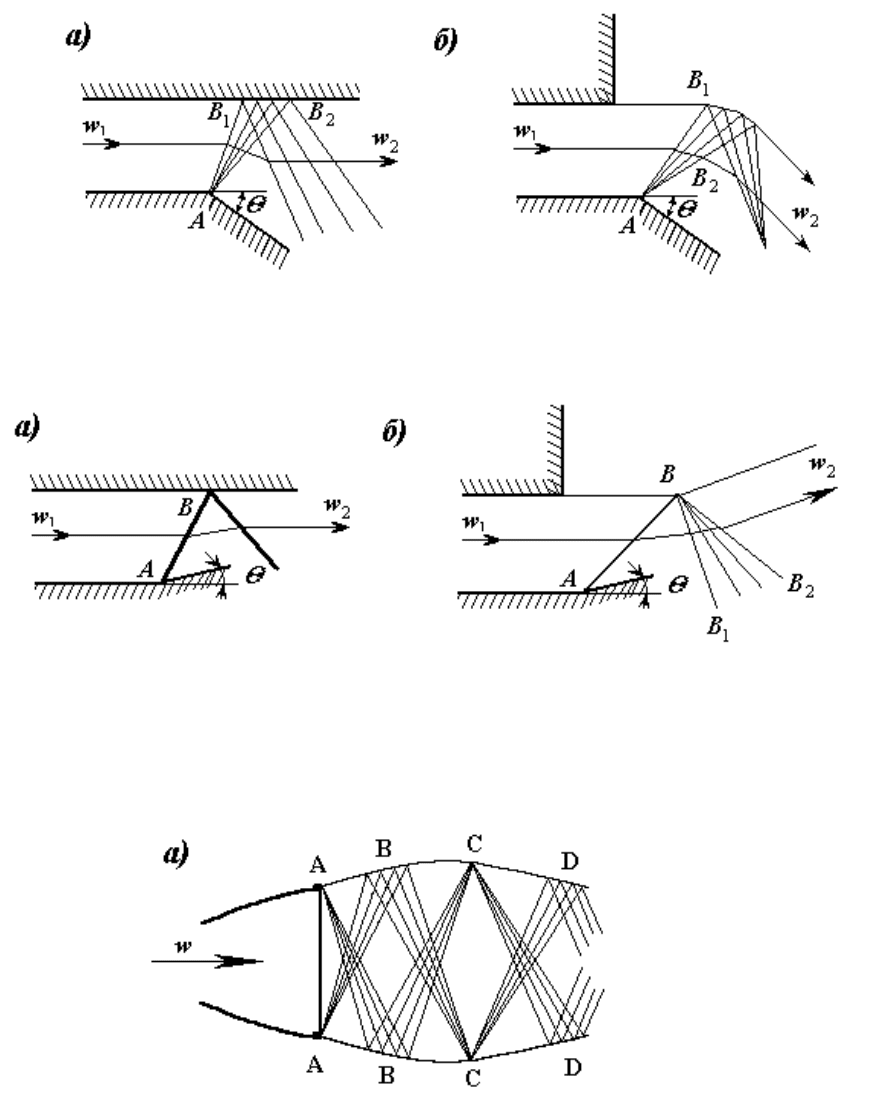
При пересечении волн давления они проникают друг через друга почти не
взаимодействуя, но отражаются от стенок и границ потока газа. На рисунках
10.12, 10.13, 10.14 приведены примеры косых скачков, отражающихся от
твердых стенок и границы струи газа.
Рисунок 10.12 - а) обтекание внешнего тупого угла при наличии стенки; б) то же, но
для поверхности струи
Рисунок 10.13 - а) внутреннее обтекание тупого угла при наличии стенки; б) то же
для поверхности струи
Режим неполного расширения газа в сопле
18
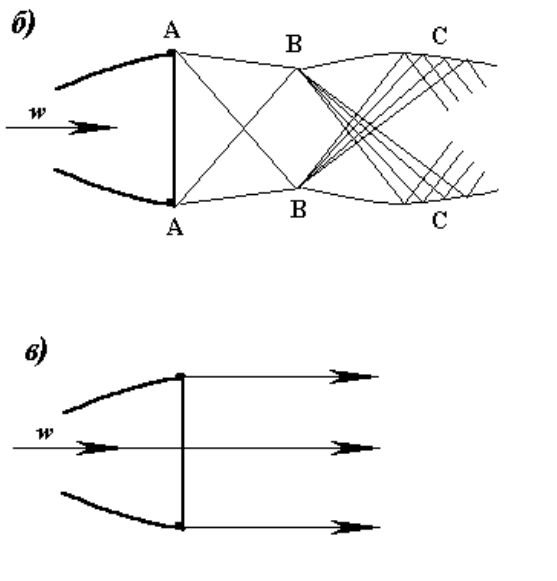
Режим перерасширения газа в сопле
Расчетный режим работы сопла
Рисунок 10.14 - Структура сверхзвукового потока за соплом Лаваля
19
