Лекции - Решение обыкновенных дифференциальных уравнений

Подождите немного. Документ загружается.

Впрактике вычислений в качестве приближенного решения

принимается значение

как имеющее более высокий порядок

точности.

Величина







kqE

(74)

называется контрольным членом.

5.2.2.3.Контрольные члены для методов Рунге-Кутта.

1)Методы(21)

321

















kkk

и(16)

201

kyy 



удовлетворяют условию (72). Контрольный член записывается в

данном случае ввиде:

321

kkk





и имеет порядок

 

0 h

2)Классический метод Рунге-Кутта(22)

4321

kkkk







и метод (16) также удовлетворяют условию (72). Контрольный член

записывается ввиде:

4321

kkkk





и имеет порядок

 

0 h

3)Мерсон предложил следующую модификацию классического

метода Рунге-Кутта:

 

004

003

002

001

541











































































xfhk

yxfhk

kkk

(79)

Формула (79) и формула третьего порядка

243

5431

kkkk





(80)

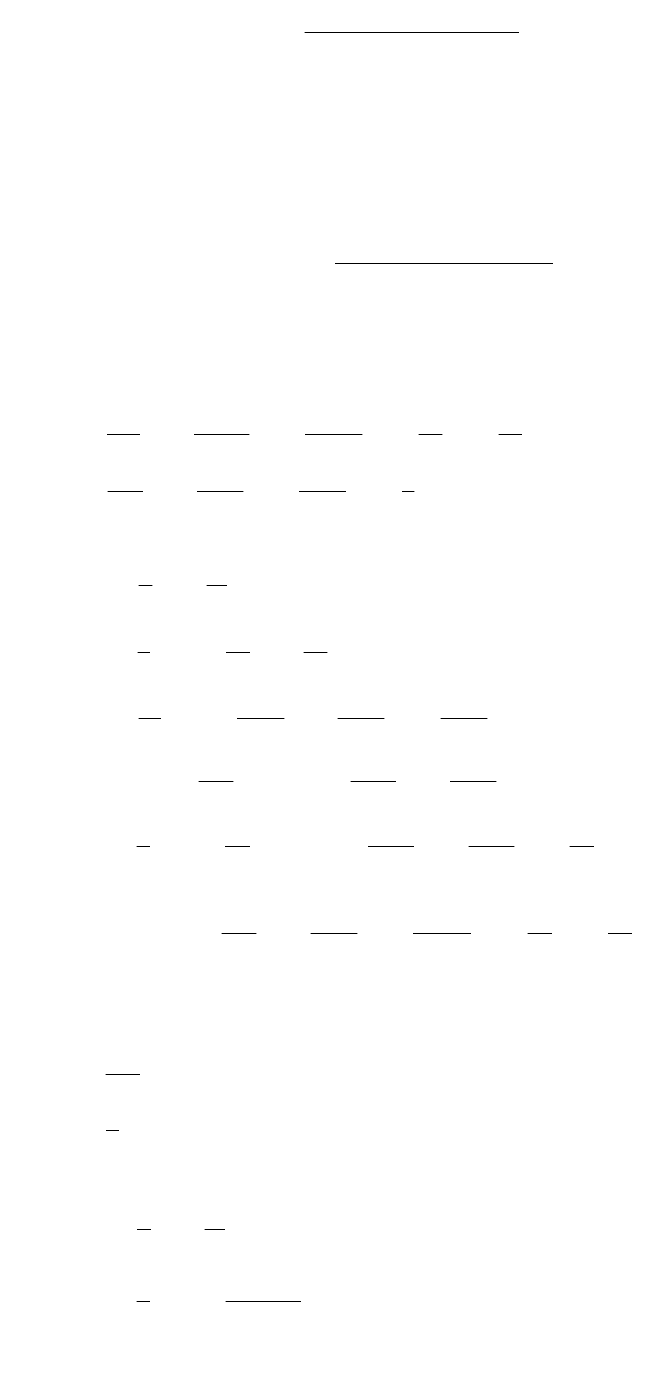
удовлетворяют условию (72). Контрольный член записывается в

данном случае ввиде:

892

5431

kkkk





и имеет порядок O(h

Наболее узком, чем (1), классе линейных уравненийвида

 

cybxayxfy  ,'

(82)

формула (80) имеет не третий, а пятый порядок точности. Порядок

точности формулы (79) остается по-прежнему равным четырем.

Поэтому величина

892

5431

kkkk







служит главным членом локальной погрешности формулы (79) и

имеет порядок O(h

4)Фельберг предложил множество методов, удовлетворяющих

условию (72). Например, формулы 4-го и 5-го порядков:

 

56430

28561

12825

6656

135

654310

kkkkkyy 

 

4104

2197

2565

1408

216

54310

kkkkyy 

 

2197

7296

2197

7200

2197

1932

321004

21003

002

001













































kkkyhxfhk

kkyhxfhk

xfhk

yxfhk

(84)

4104

1859

2565

3544

4104

845

513

3680

216

439

54321006

4321005





























kkkkkyhxfhk

kkkkyhxfhk

Контрольный член записывается в виде:

65431

75240

2197

4275

128

360

kkkkkE 

и имеет порядок O(h

5)Инглендом построены следующие формулы четвертого и

пятого порядков:

 

,1251623514

336

65410

kkkkyy 

 

4310

kkkyy 

 

,2,

32004

003

002

001

kkyhxfhk

yhxfhk

xfhk

yxfhk



































(87)

 

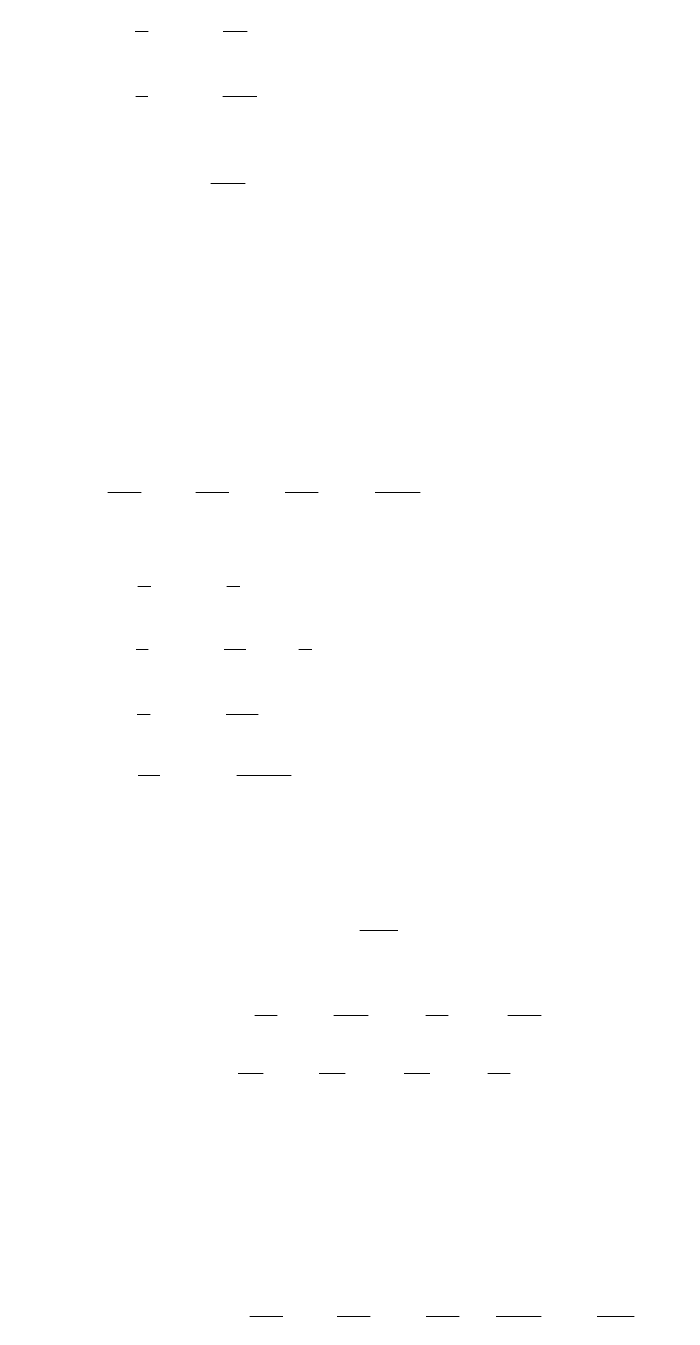
.3785454612528

625

,107

54321006

421005





























kkkkkyhxfhk

kkkyhxfhk

Контрольный член:

 

65431

1251622122442

336

kkkkkE 

имеет порядок O(h

5.2.3.Оценка погрешности с помощью нелинейного

контрольного члена.

Для приведенных в предыдущем разделе методов оценка

локальной погрешности выражалась с помощью линейной

комбинации (74) нескольких значений правой части

дифференциального уравнения. Однако существуют и другие

способы оценки локальной погрешности. Вкачестве примера можно

привести формулу типа Рунге-Кутта четвертого порядка точности:

 

1377

250

135

170

162

54310

kkkkyy 

 

1002

001

















kyhxfhk

yxfhk

 

,908123

128

321004

21003





























kkkyhxfhk

kkyhxfhk

(84)

 

,54412242025345

10000

4321005













 kkkkyhxfhk

выражение для погрешности формулы на шаге

 

101

0 hyhxy 



в виде нелинейного контрольного члена Скрэтона:

 

0 h









Где

153

170

4321

5431

kkw

kkkkv

kkkku







Полученное значение решения y

можно уточнить, если прибавить к

нему оценку локальной погрешности,т.е. в качестве приближенного

решения взять сумму:

 



yy

Врезультате получаем новую формулу пятого порядка точности

 

1377

250

135

170

162

54310

kkkkyy





использующую пять вычислений правой части на одном шаге. Ноэта

формула уже не является формулой типа Рунге-Кутта (7), поскольку

величина

 

yyy 

не выражается линейно через

6.Интегрирование с переменным шагом. Автоматический

выбор шага

интегрирования.

Досих пор рассматривался такой процесс решения задачи(1),

(2),когда формула Рунге-Кутта применялась с одной и той же

величиной шага интегрирования во всей области вычисления

решения вне всякой зависимости от характера поведения решения.

Вэтом случае говорят, что решение задачи получено с

постоянным шагом интегрирования. Применение переменного шага

интегрирования позволяет учитывать характер поведения решения и

уменьшить общее число шагов, сохранив при этом требуемую

точность приближенного решения. Тем самым могут быть снижены

объем работы и машинное время и замедлен рост вычислительной

погрешности.

Имея в распоряжении способы (53), (54), (71), (73) оценки

погрешности метода, величину шага интегрирования можно

выбирать автоматически в процессе счета.

6.1.5Алгоритм выбора с помощью удвоения и деления шага

пополам. Пусть



n+1

—оценка локальной погрешности метода на шаге

h, допущенной при вычислении приближенного значения решения

n+1

в точке x

+5h. Если оценка превосходит некоторую наперед

заданную границу :





1n

, (90)

то считается, что значение y

n+1

решения не удовлетворяет

предписанной точности и шаг h объявляется неприемлемым.

Полученная точка x

+ h и значение y

n+1

исключаются из

рассмотрения. Выбирается новое значениешага

 

h 

и вновь по той же формуле Рунге-Кутта вычисляется значение

решения в точке y

n+1

в новой точке x

+ h

(1)

. Если опять выполняется

условие (90), то шаг снова делится пополам, и вычисления

повторяются. Так происходит до тех пор, пока при какой-то величине

шага h

оценка локальной погрешности не станет меньше :





1n

. (91)

После этого считается, что решение дифференциального уравнения

продолжено до точки x

n+1

5= x

+ h

. Дальнейшее интегрирование

производится из точки x

n+1

5с шагом h

n+1

, который выбирается

описанным ниже способом.

Если оценка локальной погрешности на шаге h

= x

n+1

5—x

удовлетворяет неравенству







1

, (92)

где K —некоторая константа, то считается, что достигнута точность,

значительно превышающая заданную, и шаг интегрирования

удваиваются:

hh 



Если выполняется неравенство







1n

, (93)

то считается, что полученное в точке x

n+1

решение удовлетворяет

заданной точности и шаг интегрирования остается без изменения:

hh 

1

Таким образом, на тех участках изменения независимой

переменной, где достигается высокая точность приближенного

решения, шаг интегрирования возрастает, а там, где точность не

достигается, шаг интегрирования сокращается до необходимых для

ее достижения значений. Тем самым обеспечивается выбор величины

шага в зависимости от характера поведения решения

дифференциального уравнения. Константа K обычно полагается

равной



, где



—порядок используемой оценки локальной

погрешности метода. Обычно



= s + 1, а s —порядок формулы

численного интегрирования.

6.2.5Выбор максимальной для заданной точности длины шага.5

Так как оценка



n+1

локальной погрешности метода равна с

точностью до членов более высокого порядка малости главному

члену локальной погрешности метода, то в силу(9)

 











. (94)

Если оценка



n+1

погрешности превосходит заданную границу :





1n

то считается, что значение y

n+1

решения не удовлетворяет

предписанной точности и шаг h объявляется неприемлемым.

Полученная точка x

+h и значение y

n+1

исключаются из рассмотрения.

Вэтом случае новый размер шага выбирается не последовательным

делением пополам, а с помощью соотношения:





где



находится из условия выполнения равенства

 







. (96)

Из(94), (96) следует,что











. (97)

Здесь



< 1и новое значениешага









(98)

меньше предыдущего.

Если первоначальная оценка



n+1

локальной погрешности метода

не превосходит заданную границу :





1n

то считается, что полученное приближение y

n+1

к решению

удовлетворяет заданной точности и значение x

+h независимой

переменной принимается в качестве следующего узла

n+1

интегрирования. Дальнейшее интегрирование осуществляется из

точки x

n+1

с шагом h

, который определяется с помощью соотношения

(98). Теперь



1и h



5h.

Преимущество данного алгоритма выбора шага заключается в

большей гибкости по сравнению с описанным в предыдущем разделе

способом. Это приводит к более сглаженному изменению шага

интегрирования и, как следствие, к сокращению общего количества

шагов и снижению вычислительных затрат.

Вдействительности берется несколько меньшая, чем

определяется с помощью (98), величина шага:









. (99)

Это делается для того, чтобы избежать тех шагов, на которых не

достигается требуемая точность.

6.3.5Использование различных характеристик точности.5

Автоматический выбор шага интегрирования имеет важный

аспект, о котором надо помнить при практической реализации

алгоритма на ЭВМ. Дело в том, что для достижения заданной

точности может (в зависимости от алгоритма выбора шага)

происходить большое число делений пополам шага интегрирования

или величина



, вычисляемая по формуле (97), оказывается

настолько малой, что вновь определяемая длина шага h не вызывает

изменения независимой переменной,т.е. в условиях машинной

арифметики выполняется равенство

xhx 

. (100)

Равенство (100) выполняется тогда, когда текущее значение h

станет по абсолютной величине меньше минимального

положительного числа, представимого на данной ЭВМ. Без проверки

условия (100) во время работы программы с автоматическим выбором

шага может произойти зацикливание. Этого можно избежать, если

вместо верхней границы локальной погрешности метода, которая

может оказаться слишком малой в сравнении с порядком искомого

решения, задавать число верных цифр в приближенном значении

решения. Это позволяет более осторожно подходить к определению

точности приближенного решения с учетом длины разрядной сетки

машины.

Ясно, что при задании ограничения сверху для ошибки в виде

допустимой абсолютной погрешности фиксируется разряд,

соответствующий самой младшей верной цифре числа, а не число

верных цифр в нем. Врезультате количество требуемых верных цифр

в приближенном решении становится зависимым от порядка

искомого решения и может превзойти длину разрядной сетки

вычислительной машины и быть не достижимым для даннойЭВМ.

Втаких случаях более целесообразно использовать в алгоритме

выбора шага не абсолютную, а относительную погрешность



Однако при этом надо следить за тем, чтобы решение не обращалось

в нуль.

Более гибким является использование меры погрешности. Мерой

погрешности приближенного значения y называется величина



определяемая соотношением:

















(106)

где P —некоторое фиксированное положительное число.

Другим эффективным средством может служить ограничение

на число последовательных делений шага интегрирования,

совершаемых в одной точке, или ограничение снизу на величину

шага интегрирования. Если после значительного уменьшения шага в

одной точке (например, 10

раз) точность по-прежнему не

достигается, то, как правило, это свидетельствует о том, что явный

метод типа Рунге-Кутта не подходит для решения данной задачи.

Указанный прием позволяет получить в процессе счета

полезную информацию о характере решаемой задачи, обнаружить

сильное измельчение шага интегрирования, избежать большого

увеличения числа шагов и затрат машинного времени.

Для системы уравнений с проверкой на точность могут

вычисляться либо все компоненты решения, либо некоторые из них, в

частности одна компонента. При этом контроль точности может

вестись поеомпонентно или по норме. Если контроль ведется

покомпонентно, то для различных компонент могут использоваться

как различные характеристики точности (абсолютная, относительная

погрешности, мера погрешности), так и разные допустимые значения

погрешности.

Контроль точности по норме означает, что контролируется

некоторая норма оценки погрешности



. Часто используются

нормы:







max













Извышеизложенного следует, что формулы Рунге-Кутта очень

хорошо приспособлены для интегрирования с переменным

шагом,т.к. они позволяют легко менять шаг интегрирования и при

этом не требуют никаких дополнительных вычислений и

преобразований.

III. Многошаговые методы решения обыкновенных

дифференциальных

уравнений.

1.5Общее представление многошаговых методов.5

Многошаговым называется численный метод решения задачи

Коши (2.1), (2.2), который может быть задан формулой:

 

nknknnknknkn

yyyxxxfFy ,...,,;,...,,;

11 



. (1)

Здесь значение решения y

n+k

и точке x

n+k

определяется через

значения решения в k точках, предшествующих x

n+k

. Такой метод

называется k-шаговым.

Изкласса (1) можно выделить многошаговые методы вида:

 

 

 





ininiini

yxfhy

0 1



0



, (2)

применяемые на сетке с постоянным шагом

hnxx



,0n

1, 2,…,

 

hxN

/

. (3)

Разность между наибольшим и наименьшим значениями индекса

неизвестной функции y

, входящей в уравнение (2), равнаk. Поэтому

соотношение (2) является разностным уравнением k-го порядка,

общее решение которого зависит от k параметров. Чтобы выделить

единственное решение этого уравнения, необходимо задать k

дополнительных условий на функцию y

. Этими дополнительными

условиями являются значения функции y

при i = 0, 1,..., k-1, которые

предполагаются известными.

Если искомое решение y

n+k

входит в правую часть этого уравнеия,

что бывает, когда



 0, то формула (2) определяет неявный метод.

Если



= 0, то искомое решение в правую часть не входит и

уравнение (2)определяет явный метод.

Наряду с (2) используется также следующая запись разностного

уравнения:

   













inini

ini

yxfhy



. (8)

Уравнения (2) и (8) называются также конечно-разностными схемами.

2.Построение разностных схем методом неопределенных

коэффициентов.

Коэффициенты





выбираются таким образом, чтобы

разностное уравнение (2) аппроксимировало дифференциальное

уравнение (2.1) с достаточно гладкой правой частью с некоторым

порядкомs. Это означает, что невязка



, которая получается после

подстановки точного решения y(x) дифференциального уравнения

(2.1) в разностное уравнение (2):

   

ini

xyhxy

















, (9)

является величиной 0(h

s+1

). Число s называется порядком

аппроксимации, или степенью разностного уравнения (2). Величина

knkn







(10)

называется погрешностью аппроксимации дифференциального

уравнения (2.1) разностным уравнением(2).

Другими словами, погрешность аппроксимации — это невязка,

которая получается после подстановки точного решения

дифференциального уравнения в разностное уравнение(8).

Степень s разностного уравнения (2) определяется только

коэффициентами





этого уравнения и не зависит от того

конкретного дифференциального уравнения, для решения которого

оно применяется.

Для того, чтобы величина



n+k

и погрешность аппроксимации r

n+k

не изменялись при умножении разностного уравнения (2) на

произвольную постоянную, вводится нормировка разностного

уравнения с помощью дополнительных условий, налагаемых на

коэффициенты уравнения. Обычно полагают:

1



, (16)







. (17)

При выполнении условия (16) уравнение (2) можно записать:

 

 



 





0 0

ininiinikn

yxfhyy



. (18)

Вэтом случае невязка



n+k

(9) называется локальной погрешностью

формулы (18).

3.Устойчивость многошаговых методов.

Метод (2) сходится, если для каждой задачи из рассматриваемого

класса (2.1), (2.2):

 

0max 



Nnk

yxy

, при

0h

. (23)

Тообстоятельство, что разностная схема (2) аппроксимирует

дифференциальное уравнение (2.1) с некоторым порядком s



1, еще

не означает, что решение разностной задачи (2) сходится к решению

дифференциальной задачи (2.1), (2.2).

4. Некоторые явные конечно-разностные формулы.

Вявных формулах неизвестное значение y

n+1

не входит в правую

часть, поэтому явные формулы записываются в виде:

 











ininiknkn

yxfBhAyy

. (41’)

4.1.5Экстраполяционная (явная) формула Адамса.5

Таблица1.

Примеры конечно-разностных явных методов Адамса

Порядок Коэффициенты Степень

Локальная

k A B

s погрешность

1 1 1 1 h

(2)

/2

2 ½ -1 3 2 5 h

(3)

/12

3 1/12 5 -16 23 3 3 h

(4)

/8

4 1/24 -9 37 -59 55 4 251 h

(5)

/720

5 1/720251 -12742616-2774 1901 5 95h

(6)

/288

Если интерполяционный многочлен представить в форме

интерполяционного многочлена Ньютона для равных промежутков

   









nnknk

ittt

fhtxLxL

1...1

, (48)

Где

f

— конечная разность i-го порядка назад функции

y'(x)5=5f(x,5y(x)) в узле x

, x = x

+th, то формула численного

интегрирования может быть получена в разностной форме:

   









inn

fhxyxy



. (50)

Отбрасывая в (50) остаточный член



n+1

, получаем разностное

уравнение, эквивалентное (41), но представленное в разностной

форме:

)....

17280

5257

60480

19087

288

720

251

(

5432

knn

nnnnnnnn

fff

ffffffhyy









(53)

5. Часто используемые неявные конечно-разностные

формулы.

Внеявных формулах неизвестное значение y

n+1

входит в правую

часть, поэтому неявные формулы записываются в виде:

 









ininiknkn

yxfBhAyy

. (41’’)

5.1.)Интерполяционная (неявная) формула Адамса.

Таблица>1.

Примеры конечно-разностных неявных методов Адамса

Порядок Коэффициенты Степень

Локальная

k A B

s погрешность

1 1 0 1 1 -h

(2)

/2

1 ½ 1 1 2 -h

(3)

/12

2 1/12 5 8 -1 3 -h

(4)

/24

3 1/24 9 19 -5 1 4 -19h

(5)

/720

4 1/720251 646 -264 106 -19 5 -3h

(6)

/160

Неявную формулу Адамса можно представить в разностной формуле:

).'...

24192

275

60480

863

160

720

(

111









knnn

nnnnnnn

ffff

fffffhyy



(70)

Коэффициенты явной



и неявной



' разностных формул Адамса

обладают следующими свойствами:

iii







, (73)







. (74)

Т.к.



'<0, а



>0, то из (73) следует, что



монотонно убываюти



'

. (75)

Отсюда следует, что константа в главном члене локальной

погрешности у интерполяционной формулы Адамса всегда меньше,

чем у экстраполяционной формулы Адамса той же степени.

6.Особенности поведения многошаговых методов на больших

интервалах интегрирования.