Лекции по СИИ
Подождите немного. Документ загружается.


Алгоритм 4.3
Исходные данные: обучающая выборка, то есть последовательность пар векторов
( , )
t t
u y
для t=1,2,3..T, β —
коэффициент скорости обучения, ε - параметр точности обучения,
max
Q
-максимальное количество эпох.
Выход:
( ) ( )
( )
l l
ij
W w
размером
1
, 1, 2,...,
l l
N N l L
.
Шаг 0: Инициализация весовых коэффициентов.
1
1, 2,3.. , 1, 2... , 1,2,..
l l
Циклы l L i N j N
Синаптическим весам датчиком случайных чисел присвоить малые величины из интервала (-1,1). t=1.
Шаг 1: Подать на вход сети обучающий вектор
t
u
.
Шаг 2:Прямой ход
1
1, 2,3.. , 1, 2... , 1,2,..
l l
Циклы l L i N j N
вычислить выходные сигналы j - ого нейрона в этом слое, следующим образом:
1
1
1
( )
i
N
l l l
j ij i
i
x f w x
, где
(0) t
i i
x u
- входные значения. И выходные сигналы сети:
L
j j
y x
Шаг 3: Обратный ход (коррекция весовых коэффициентов).
1 1
1, 2,3.. , 1, 2... , 1,2,..
l l
Циклы k L i N j N
Вычислить
( )
( ) ( ) ( ) ( 1)
( ) (1 )
L t
k k k k k
L L L L
jk jk k j
y y y y
w w x
Здесь же в циклах:
1
1
1 1
1
( ) ( ) ( ) ( 1)
1,..,1
1,..,
(1 )( )
i
l
N
l l l l l
j j j jk k
k
l l l l
ij jk j j
l L
i N
x x w
w w x
Шаг 4.
1 [ ] 1.
t
t t T do to
T
4.4.3 Сети встречного распространения
Объединение разнотипных структур в один приводит к новым свойствам.
Нейронные сети встречного распространения - это гибридные сети, состоящие из входного слоя нейронов и слоев
нейронов Кохенена и Гросберга. Эти сети по своим характеристикам существенно превосходят сети с однотипными нейронами
(?).
Нейроны слоя Кохенна реализуют функцию порогового суммирования взвешенных входов, однако, в отличие от
остальных слоев нейрон слоя Кохенна с максимальным значением взвешенной суммы на заданных входной вектор называется
победителем, на его выходе формируется значение 1, а на выходах остальных - 0.
Слой Кохенна обучается без учителя на основе самоорганизации, т.е. самообучаемый слой. Число входов каждого
нейрона этого слоя равно размерности вектора параметров объекта. А количество нейронов совпадает с требуемым числом
классов на которые необходимое разбить объекты. Нейроны слоя Гросберга на выходе выдают величины весов
ij
v
, которые
связывают с победителями нейронов Кохенана. В отличие от самообучающегося слоя Кохенена, слой Гросберга обучается с
учителем.
Отличие от стандартной схемы обучения заключается в том, что подстройке подвергаются только те веса нейронов слоя
Гросберга, которые соединены с ненулевым нейроном Кохенена.
1
u
2
u
m
u
1
y
2
y
m
y
11
w
2 ,m n
w
11
v
,2n m
v
*
1
u
*
2
u
*
m
u
*
1
y
*
2
y
*
m
y
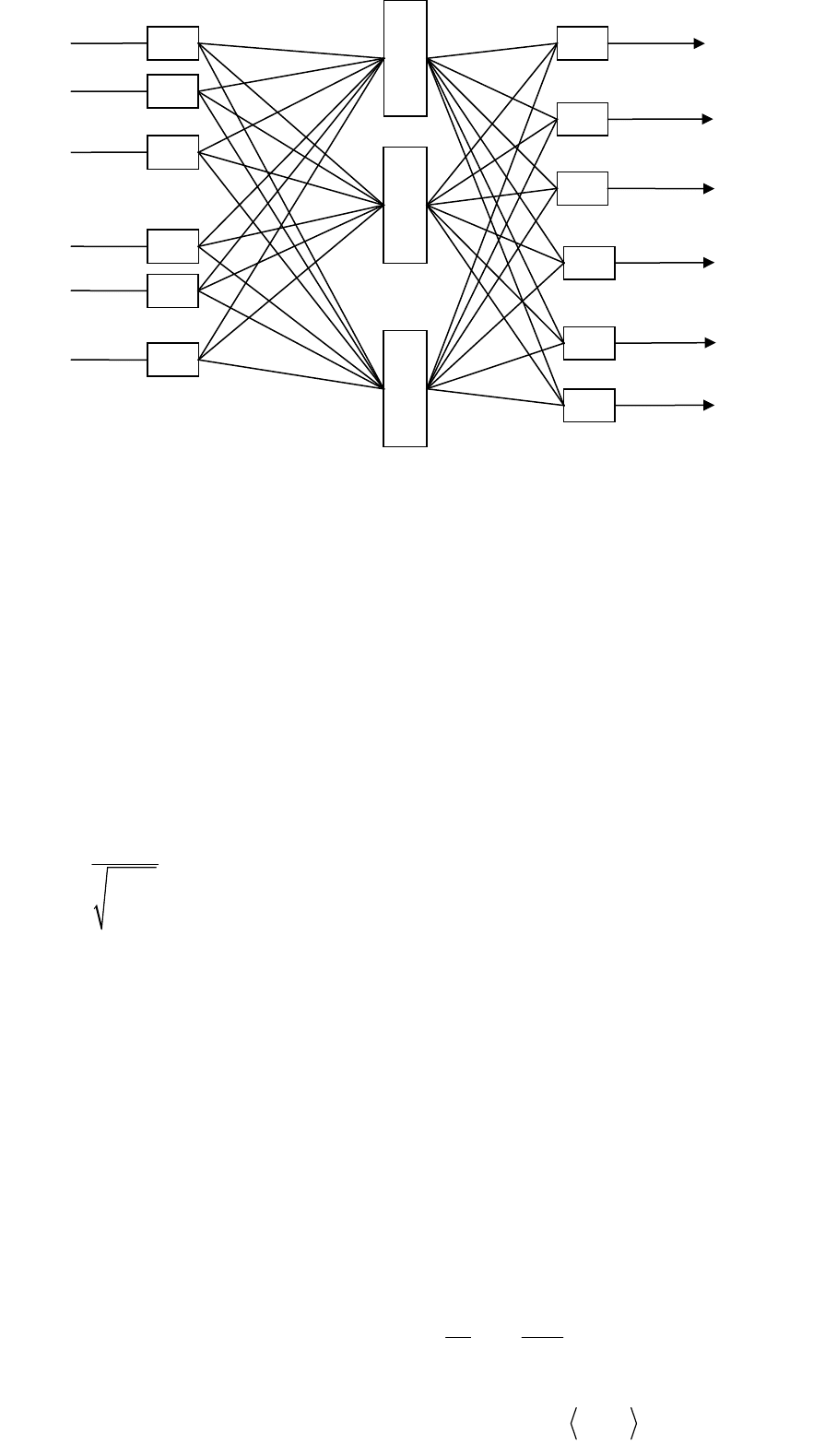
Отличие сети встречного распространения заключается так же в особенностях функционирования. В соответствии с
приведенной на рисунке структурой на вход сети подаются нормализованные единичные векторы u, y. А на выходе
формируются их нормализованные аппроксимации с волнами. При обучении входные вектора подаются как на вход, так и на
выход.
Реализуется свойства ассоциативной памяти, заключающееся в том, что предъявление на вход только вектора y или u при
отсутствии другого приводит к порождению на выходе как
u
, так и
y
.
4.4.4 Обучение сети встречного распространения.
Нормализованный вектор — вектор единичной длины.
Перед обучением сети предварительно проводят нормировку векторов обучающей выборки.
1 2,
1 2,
2
1
( , ..., )
ˆ ˆ ˆ ˆ
( , ..., )
ˆ
, 1,.., (4.27)
( )
2
r
r
i
i
r
j
j
x x x x
x x x x
x
x i r
x
x uy
r m
Если осуществить нормировку, а так же после каждого процесса осуществить нормировку каждого нейрона, то в
качестве близости входных векторов и векторов нейронов можно рассматривать скалярное произведение между ними
1
,
r
k
ki i
i
w x w x
.
1
( ,..., )
k
k kr
w w w
— строка матрицы W.
Наименьшим будет расстояние до того нейрона, у которого будет скалярное произведение с которым у входного вектора
максимально.
Алгоритм 4.4
Входные данные: обучающая выборка
( , ), 1, 2,...
k k k
x u y t T
:
- начальный коэффициент скорости обучения слоя К.
[0,7; 0,9]
- коэффициент скорости обучения слоя Г.
[0,1;0,3]
Выход:
2 2
( ) , ( )
ij n m ij m n
W w V v
Шаг 0: Весовым коэффициентам
, , 1, , 1, 2
ij ij
w v i n j m
присвоить малые случайные значений и произвести
единичную нормировку матриц W,V по строкам. t=1.
Шаг 1: Для вектора x^t вычислить скалярные произведения
1
, , 1, 2...
m
j t
j j i
i
d w x w x j n
1
u
2
u
m
u
1
y
2
y
m
y
11
w
2 ,m n
w
11
v
,2n m
v
*
1
u
*
2
u
*
m
u
*
1
y
*
2
y
*
m
y

Шаг 2: Выбрать нейрон k 1<= k <= n с наибольшим скалярным произведением
k
d
.
Шаг 3: установить выход
1
k
z
, выходы всех остальным нейронов слоя Кохенена = 0
! 0
i
i k z
Шаг 4:
( ), 1, 2...2
t
ki ki i ki
w w x w i m
Шаг5:Подать выходной вектор слоя Кохеннан на слой Гросберга и скорректировать веса по формуле:
( ), 1, 2
t
ik ik i ik
x i m
Шаг 6: Уменьшить значения
и
, и изменить
1 1
t
t t T do to
T
.

10.12.2009
Глава 5. Распознавание образов
§5.1 Общие сведения о моделях распознавания образов
5.1.1 Предмет и проблемы распознавания образов
В своей повседневной жизни человек легко справляется с этой проблемой.
Различают два аспекта теории распознавании образов:
- биологический
- технический
В первом случае исследуются процессы распознавания человеком и другими представителями животного мира и
создание более менее адекватных моделей математических, технических.
При втором подходе речь идет о создании эффективных методов и технических устройств для распознавания конкретных
образов – зрительных, слуховых и т.д. Конструктор может прибегать к аналогиям из животного мира или использовать
абстрактные технологии.
Принципы:
- заложить в компьютер как можно больше известных образов и использовать их при распознавании
На первой стадии системы распознавания обязательно обрабатывают изображение и выделяют характерные признаки:
качественные и количественные, таким образом, количество информации для распознавания уменьшается
- идея обучения
5.1.2 Основные понятия теории распознавания образов
Образ (или класс) – отдельные предметы или явления, которые необходимо распознать, обладающие общими друг для
друга свойствами и имеющие некоторые отличительные свойства.
Классом или образом можно назвать множество предметов или объектов, обладающих некоторыми общими свойствами,
как правило, имеется набор классов или алфавит классов – А
1 2
{ , ,..., }
n
A A A
(5.1)
i
A
– отдельный i - й класс
n – общее число классов
Если n = 1 , то никакого распознавания нет, т.е. в задачах распознавания актуальна при n>=2.
Объект (реализация, образец) – каждый класс в алфавите образов может быть представлен некоторым количеством
объектов или реализацией. Совокупность различных реализаций для всех классов образует множество возможных реализаций
1 2
{ , ,..., }
n
B b b b
(5.2)
В большинстве практических задач N конечно и N>>n (много больше), однако если значение признака изменяются
непрерывно, то значение N бесконечно.
Признак класса – при введении класса указывается, что в класс объединяются образы, имеющие общие свойства, эти
свойства и составляют признаки данного класса.
Признаки обычно задаются количественными значениями.
Для простоты будем считать, что все классы характеризуются одним и тем же количеством признаком – m.
Обозначим совокупность признаков для данного алфавита А в виде вектора
1 2
( , ,..., )
m
u u u u
(5.3)
Практически числовые значения признаков изменяются в некоторых пределах. Каждый признак
k
u
может принимать
значения из совокупности
1 2
{ , ,..., }
n
k k k k
u u u u
(5.4)
Каждая конкретная реализация задается совокупностью значений признаков
1 2
( , ,..., )
j j j
j m
b u u u
(5.5), которая называется описанием реализации.
Количество возможных реализаций при m признаках и r градациях может быть определено по формуле
m
N r
(5.6)
В большинстве задач распознавания имеется два этапа:
1. Обучение распознаванию на заданном количестве эталонных образов принадлежность которых к определенному
классу известна.
2. Собственное распознавание – предъявляется объект с неизвестной принадлежностью и требуется определить, к
какому классу относится объект.
§5.2 Пандемониум Селфриджа
Система распознавания образов, предложенная Оливером Селфриджем и называемая подемониумом, состоит из
элементов, называемых демонами.
Демоны – относительно автономные сущности, выполняющие элементарные функции.
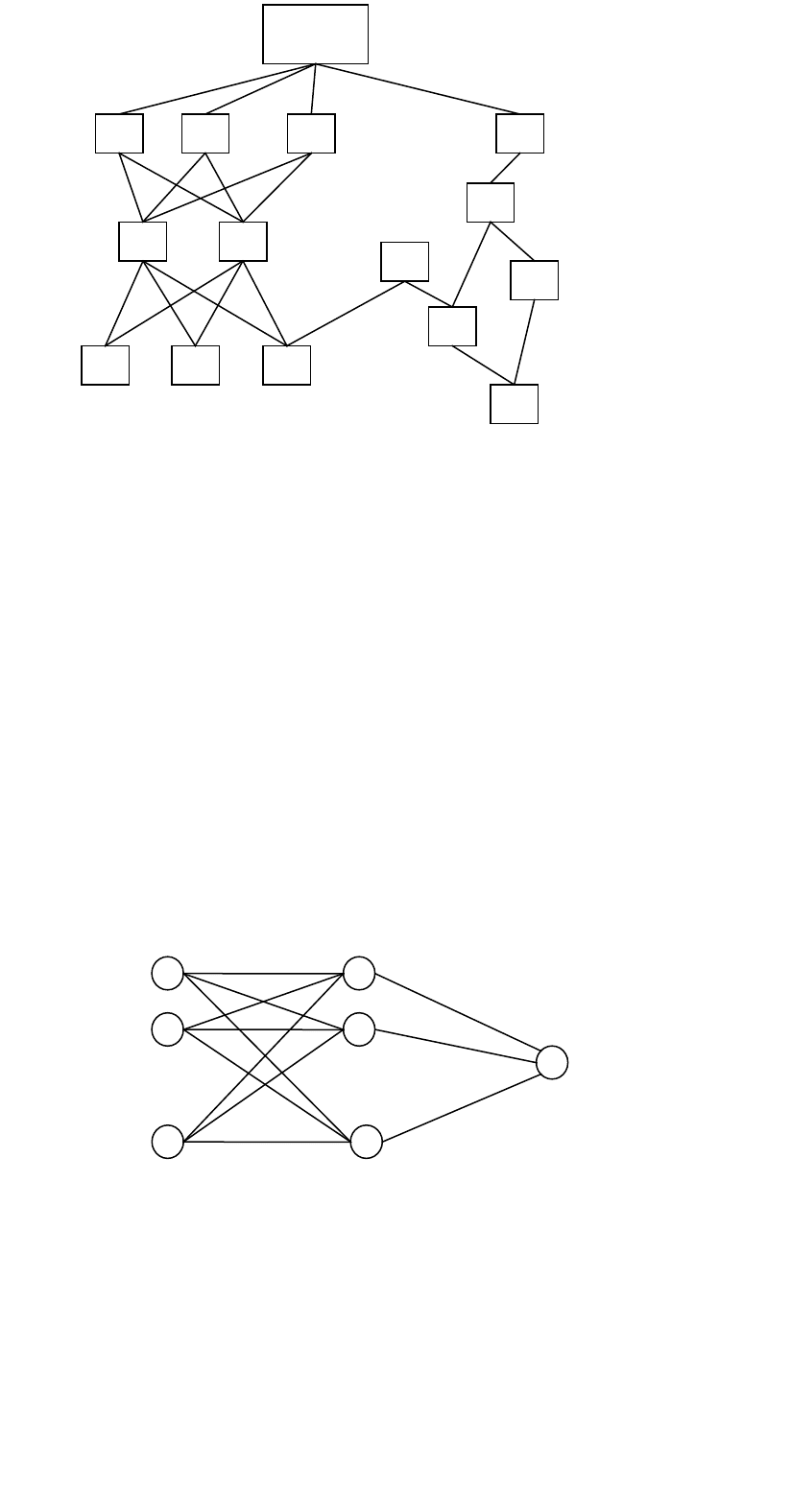
На самом нижнем уровне находятся демоны данных (играют роль светочувствительных элементов глаза)
На самом верхнем - демоны решения, которые определяют исход.
Ниже уровень – демоны понимания, каждый из которых соответствует одной из указанных категорий
Ниже – вычислительные демоны обрабатывают данные и передают их демонам понимания.
Эта идея программируется просто – демоны понимания вычисляют взвешенные суммы сигналов, поступающих от
вычислительных демоном
i – й демон понимает вычисляет свой сигнал
(5.7)
i ij j
D w d
ij
w
– весовые множители, устанавливающие значимость признаков, поступающих для суммирования.
j
d
– выходной сигнал j вычислительного демона.
Понимониум – обучающееся устройство.
§5.3 Распознавание с помощью персептронов
Одной из первых нейронных сетей, предназначенной для распознавания образов, был персептрон Розенблата, способный
обучаться на опыте.
Первоначально персептрон содержал узлы 3 типов: сенсорные узлы (соответсвуют демонам данных), ассоциативные
(вычислительные демоны), выходы a – узлов были соединены с узлами реакции или p – узлами (демоны понимания)
В отличие от понтемониума p – узел дает только 1 или 0.
Веса синапсов, ведущих к p – узлам, изменялись в процессе обучения персептрона.
Далее это идея развивалась при использовании сложных многослойных сетей.
5.4 Геометрическая интерпретация распознавания
Задача распознавания образов по признакам можно дать геометрическую интерпретацию.
Каждый объект с m признаками согласно (5.3) определяет в m – мерном пространстве признаков точку
1 2
( , ,..., )
m
u u u u
.
Демоны
решения
Демоны
понимания
Вычислител
ьные демоны
Демоны
данных
с
- узлы
-
узлы
p
- узлы
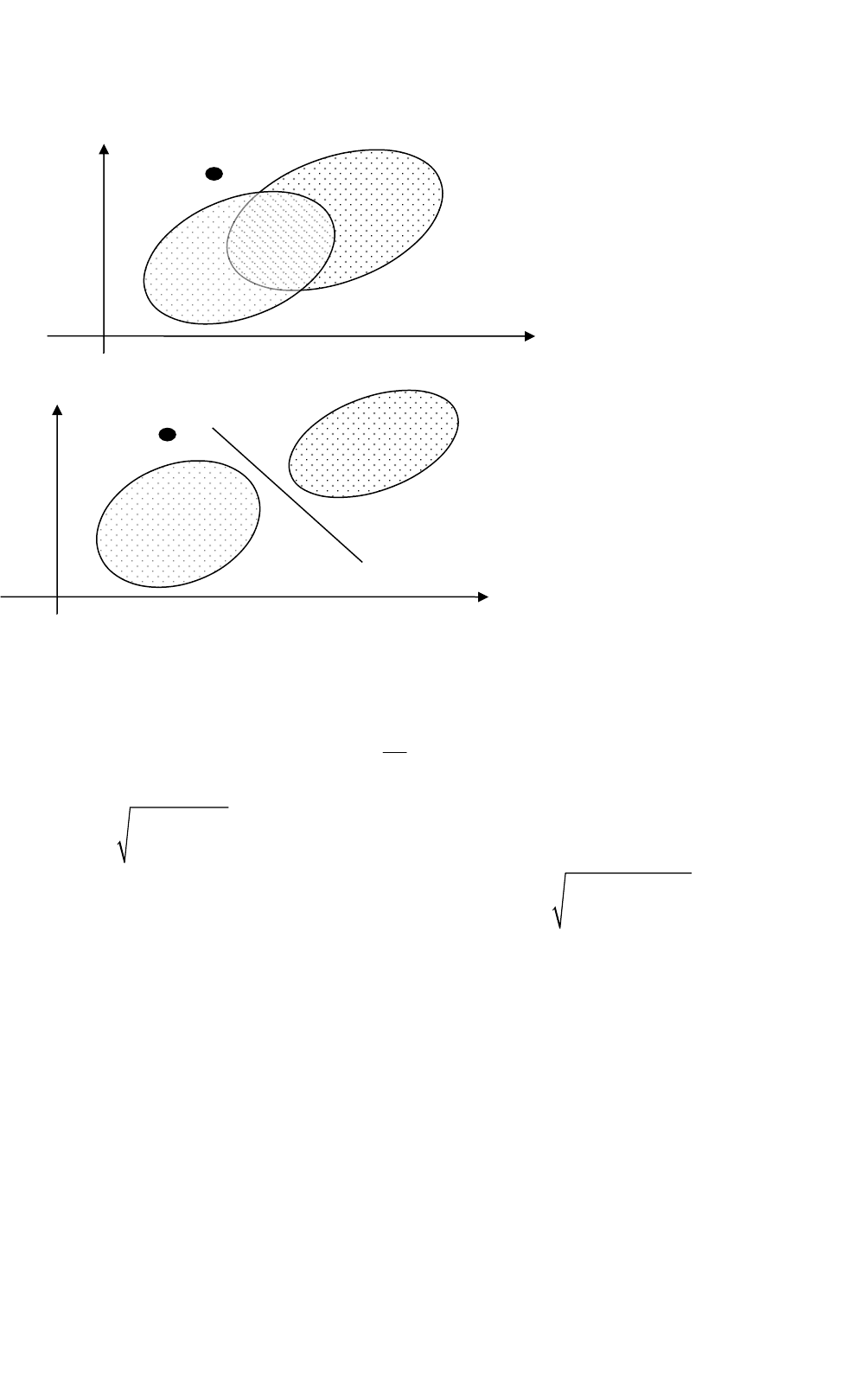
Геометрический метод распознавания основан на использовании некоторой функции принадлежности
объекта
данному классу.
Эта функция определяет меру близости объекта к некоторым эталонным множествам
Эти множества в m – мерном пространстве признаков определяют пересекающиеся или непересекающиеся между собой
множества.
m = 2
Пересекающиеся эталонные множества менее пригодны для распознавания.
Эталонные множества с помощью преобразования системы координат могут быть отделены друг от друга и т.о. между
ними может быть проведена некоторая гиперплоскость, разделяющая эти множества.
Определяя функцию близости
между объектом и эталонным множеством класса, часто используют расстояние между
этим объектом и центром эталонного множества.
Совокупность этих центров даст нам множество эталонов
1 2
{ , ,..., }
n
u u u
Каждая
k
u
– точка
1 2
{ , ,..., }, 1,
k k k k
m
u u u u k n
В евклидовой метрике m – мерного пространства расстояние между точками определяется как
2
1
( , ) ( )
m
k k
i i
i
d u u u u
(5.8)
В данную формулу удобно ввести весовые коэффициенты
2 2
1
( , ) ( )
m
k k
i i i
i
d u u w u u
(5.9)
Весовые множители нужны для отражения того факта, что отдельные признаки объектов имеют разную степень важности
для распознавания образов.
При геометрической трактовке распознавания образов прибегают к интерпретации. процесса в виде некоторого
преобразования системы координат, при котором объекты одного класса сжимаются а множества различных классов удаляются
друг от друга
Существуют линейные и не линейные способы преобразования.
В общем случае линейное преобразование задается матрицей
11 1
...
... ... ...
... ...
m
mm
w w
W
w
(5.10)
Если в исходной системе координат заданы векторы объектов
1 2
( , ,..., )
m
a a a a
и
1 2
( , ,..., )
m
b b b b
То преобразованные векторы
', 'a b
определяются соотношениями
1
1
'
' , 1,
' , 1,
m
j i ij
i
m
j i ij
i
a aW
a a w j m
b b w j m
(5.11)
А
1
А
2
b
А
1
А
2
b
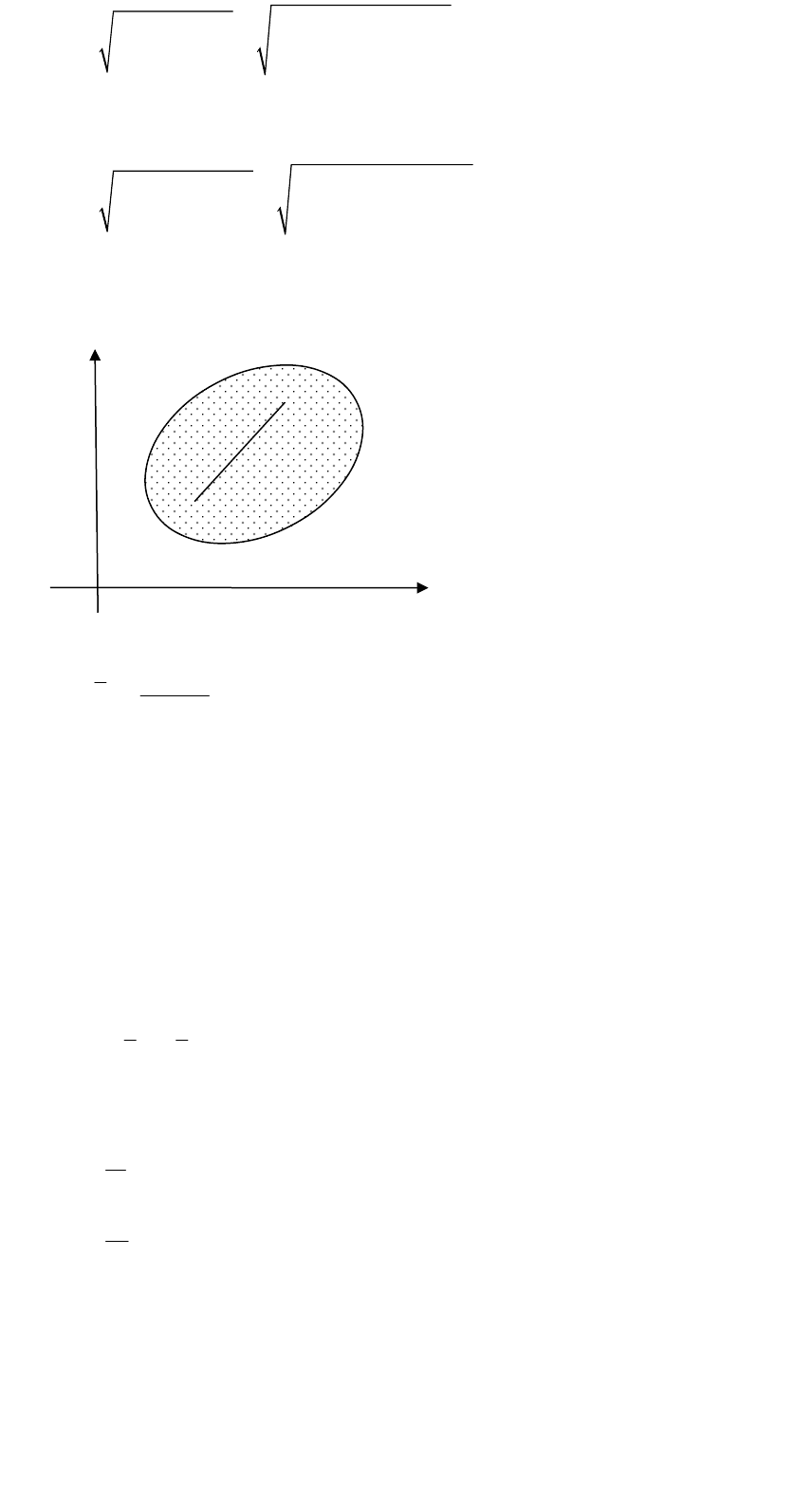
Евклидово расстояние между элементами в преобразованном пространстве будет
2
2
1 1 1
( ', ') ( ' ' ) ( )
m m m
i i ij i i
i j i
d a b a b w a b
(5.12)
Диагональные элементы матрицы преобразований W определяют масштабные коэффициенты сжатия вдоль
координатных осей, а остальные элементы матрицы поворот координатных осей.
Если в матрице преобразований все недиагональные элементы = 0 , т.е.
0,
ij
w i j
, то (5.12) принимает вид
2
2 2
1 1 1
( ', ') ( ) ( )
m n m
ii i i ii i i
i j i
d a b w a b w a b
(5.13) совпадает с (5.9).
Рассмотрим частный случай, когда поворот координатных осей не производится, а изменяется только масштаб.
Требуется определить такие коэффициенты сжатия, чтобы в новой системе координат расстояние между объектами
множества были минимальными, т.е. чтобы было минимальным расстояние между текущими точками P и Q множества
2 2 2
1 1 1
1
( ) (5.14)
( 1)
n n m
p q
ij i i
p q i
D w u u
n n
Для решения поставленной задачи требуется наложить дополнительные условия на весовые коэффициенты
Например, можно потребовать, чтобы выполнялось равенство
1
1
m
ii
i
w
(5.15)
Эта нормировка весовых коэффициентов наиболее распространена и означает, что весовые множители могут меняться от
0 до 1, и пространство признаком будет сжиматься по осям.
Помимо (5.15) используют и другие условия
1
1 (5.16)
m
ii
i
w
Т.о. задача обучения состоит в минимизации функционала (5.14) составленных для множеств А1 и А2 обозначим эти
функционалы
2
1
D
и
2
2
D
с дополнительными условием (5.15) или (5.16).
После того как обучение выполнено, решается задача распознавания.
Пусть даны два эталонных множества, и требуется определить, к какому из них относится некоторый объект b.
Для решения этой задачи в преобразованном пространстве вычисляется расстояние от точки b до каждого множества.
1
2
2 1 2
1
1 1
1
2 2 2
2
1 1
2
1
( )
1
( )
n
m
b j
i i
j i
n
m
b j
i i
j i
d u u
n
d u u
n
(5.17)
1
n
– число точек эталонного множества
1
A
.
2
n
– число точек эталонного множества
2
A
.
Решающее правило состоит в следующем:
2 2
1 1 2
2 2
2 1 2
,
,
b A если d d
b A если d d
Коэффициенты
ij
w
ищутся применительно к первому и второму множеству эталонов.
P
Q

24.12.09
Тема: Нечеткие множества и нечеткая логика
§ 6.1 Мотивации и истории зарождения нечетких множеств.
В эпоху широчайшего проникновения компьютеров в нашу жизнь. Постоянно существуют проблемы, в решении
которых человеческий интеллект оказывается важнее компьютера. Ответственные решения принимает человек, а не компьютер.
Способность принимать правильные решения в обстановке не полной или нечеткой информации. Традиционные вычисления
компьютера оказываются «слишком точными» для реального мира. Человек принимает решение на основе суждений, с самого
начала ему присуще весьма характерная нечеткость (пример — высокий человек, а какой точно рост считается высоким?).
Даже нечеткие алгоритмы используют внутри себя четкие модули.
Возникает некоторая потребность в анализе сложных явлений.
Появлением термина нечеткая логика мы обязаны Л. Заде. Он занимался проблемами математического управления в
технических системах. Основная идея состояла в том, что человеческий способ рассуждений, опирающийся на естественный
язык, не может быть описан с помощью традиционных мат. методов. В основе этого тезиса лежит то, что можно назвать
принципом несовместимости: чем сложнее система, тем менее мы способны дать точные и в то же время имеющие
практическое значение суждения о ее поведении. Для систем, сложность которых превосходит некоторый пороговый уровень -
точность и практический смысл становятся исключающими понятиями. Традиционные методы оказываются не достаточно
пригодными.
Подход на основе теории нечетких множеств. Этот подход опирается на предпосылку о том, что элементами
мышления человека являются не числа, а элементы некоторых нечетких множеств или классов объектов, для которых переход
от принадлежности классу к непринадлежности ему не скачкообразен, а непрерывен. Теория нечетких множеств представляет
собой переосмысление важнейших направлений теории математики.
При разработке интеллектуальных систем, знания редко бывают полными и достоверными. При обработке с четкими
методами возникает противоречие между обработкой нечетких данных и четких методов. Устранить это позволяет нечеткие
множества(?).
Практически все модели СИИ основаны на нечетких моделях.
§6.2 Нечеткие множества
6.2.1 Определение множества в Канторовской теории множеств и традиционная двузначная логика.
Понятие множества вводиться на основе понятия совокупности. Конечного или бесконечного числа предметов, которые
по какому-либо признаку собранные во едино. При этом предметы берут из некоторой области рассуждений. Множество
считается заданным, если заданы его элементы. Множество может быть задано различными способами.
Например:
1. перечислением элементов: А={0,2,4,6,8} (6.1)
2. описанием свойств: А = { x | х - четное число >0 и <9 }. (6.2)
3. графически - диаграмма Вейна.
4. множество может быть задано с помощью характеристической функции:
Пусть U - область рассуждений — универсальное множество (универсум).
Характеристическая функция
A
, определяющая множество A в универсуме U, есть отображение, для которого U
является областью определения, а двух элементное множество {0,1} – есть область значений.
: {0,1}
0,
(6.3)
1,
A
A
U
x A
x U
x A
Двузначная логика: относительно любых событий в этом мире всегда можно сказать, что оно или истинно или ложно.
Если значение истины представлять 1, а значение ложь — 0. В точной логике при формулировке выводов если выполняется
причина, то обязательно выполняется и следствие.
§6.2 Определение нечеткого множества
Рассмотрим снова формулу (6.3) определяющую характеристическую функции
A
. Профессор Lotfi Zadeh в 1965 году
опубликовал статью, которая называлась «Fuzzy sets», которой он расширил двузначную логику до ограниченной многозначной
оценки. Выше 0 и ниже 1, то есть в интервал [0,1] и впервые вел понятие нечеткое множество. Здесь вместо термина
характеристическая функция использовал функция принадлежности. Нечеткое множество в универсуме U определяется через
функцию принадлежности следующим образом:
А

: [0,1]
(6.4)
( )
A
A
U
x x
Величина
( )
A
x
означает субъективную оценку степени принадлежности x множеству A. Заранее не постулируется,
какого вида эта оценка. Четкое множество является частным случаем нечеткого множества.
Заметим, что нечеткое множество строго определяется с помощью функции принадлежности, таким образом, логика
определения понятия нечеткого множества не содержит какой-либо нечеткости.
Определение 6.1. Нечетким множеством A на универсуме U будем называть совокупность упорядоченных пар
{ ( , ( )) | , ( ) : [0,1]}
A A
A x x x U x U
(6.5) , составленных из элементов x универсума U и соответствующей степеней
принадлежности
( )
A
x
.
Пример:
1 2 3 4 5 6
( , 0.3),( , 0.5),( , 0.8),( , 1),( , 0.5), ( , 0)A x x x x x x
Обычно нечеткое множество отождествляется с его функцией
( )
A
x
.
Замечание: Определение нечеткого множества с помощью определения 6.1 является одним из возможных подходов
формализации нечеткости. Функция может принимать не значение из интервала, а целый интервал из интервала.
6.2.3 Основным характеристики нечетких множеств
Определение 6.2. Носителем нечеткого множества А называется обычное подмножество таких точек из универсума U,
для которых величина
( ) 0
A
x
. Носитель обозначается:
supp , ( ),
A
A S A Г
.
supp { | ( ) 0}
A
A x U x
(6.6)
Определение 6.3. Высотой нечеткого множества A называется величина
( ) sup ( )
A
x U
H A x
(6.7)
Определение 6.4. Нечеткое множество А называется нормальным, если его высота = 1, в противном случае оно
называется субнормальным.
Замечание 6.2. Иногда субнормальное нечеткое множество нормализуют на величину H(A).
Определение 6.5. Нечеткое множество A называется пустым, если
( ) 0,
A
x x U
.
Определение 6.6. Множеством α - уровня (альфа - срезом, альфа - сечением) нечеткого множества A называется
обычное, то есть четкое подмножество универсума U, определяемого формулой:
{ | ( ) }, [0,1]
A
A x U x
(6.8)
Множества строго α - уровня определяются формулой:
{ | ( ) }, [0,1]
S
A
A x U x
(6.9)
Носитель нечеткого множества является частным случаем множества строго α - уровня, то есть
0
supp
S
A A
(6.10)
Определение 6.7. Элементы множества U, для которых степень принадлежности
( ) 0.5
A
x
называются точками
перехода.
Определение 6.8. Нечеткое множество А в универсуме U (
n
U R
) называется выпуклым нечетким множеством тогда
и только тогда, когда его функция принадлежности выпукла, то есть для каждой пары точек
( , )x y U
выполняется условие:
( (1 ) ) min( ( ), ( )), [0,1]
A A A
x y x y
(6.11)
6.2.4 Операции над нечеткими множествами
Пусть А,В нечеткие множества на универсуме U.
Определение 6.9. Равенство: говорят, что А и В равны и пишут А=В, если
( ) ( ),
A B
x x x U
(6.12)
Определение 6.10. Операция включения: говорят А содержится в В, или нечеткое множество А является нечетким
подмножеством нечеткого множества В и пишут
: ( ) ( ),
A B
A B x x x U
(6.13)
Строгое включение или строгое подмножество имеет место, когда хотя бы одно из неравенств (6.13) является строгим.
Когда А является подмножеством В, т.е.
A B
, говорят что В доминирует А.
Определение 6.11. Дополнением нечеткого множества А в U называют нечеткое множество
A
с функцией
принадлежности:
( ) 1 ( ),
A
A
x x x U
(6.14)
Определение 6.12. Объединение нечетких множеств А и В в U, т.е.
A B
называют наименьшее нечеткое множество,
включающее как А, так и В с функцией принадлежности вида:
( ) max( ( ), ( )),
A B A B
x x x x U
(6.15)
Определение 6.13. Пересечением нечетких множеств А и В в U, т.е.
A B
называют наибольшее нечеткое множество,
содержащееся одновременно в А и в В:
( ) min( ( ), ( ))
A B A B
x x x
(6.16)
Есть и другие определения различных операции.
В теории нечетких множеств много разделов посвящено теории нечетких чисел.

§6.3 Нечеткая логика и нечеткие выводы
6.3.1 Нечеткая логика
Так же как и в основе четких множеств лежит четкая логика, так и в основе нечетких множеств существует нечеткая
логика.
В случае нечеткой логики можно создать неограниченное число операции, поэтому нет смысл говорит о записи всех
операции с помощью базового числа операций.
Пример: нечеткое отрицание: (аналог четкой операции не). Аксиоматически можно определить так:
1 2 1 2
:[0,1] [0,1]
0 1
(*)
( ) , [0,1]x x x
x x x x
Все функции, удовлетворяющие аксиомам (*), являются нечеткими отрицаниями.
6.3.2 Нечеткие выводы.
Важной операцией является нечеткая импликация. Нечеткие выводы, нечеткие рассуждения наиболее важный момент.
Экспертные системы, построенные на четкой логике, можно считать частным случаем нечетких экспертных систем.
Нечеткие выводы по правилам (пример). Пусть существует знание эксперта, что необходимо открыть спускной клапан,
если уровень воды поднимается. Это знание можно представить с помощью нечеткого продукционного правила, типа « если, то
» следующим образом:
если <уровень воды высокий>, то <открыть клапан>.
В нашем случае важно описать предпосылку и заключение в виде нечеткого отношения. Другими словами в исходное
выражение не попадали данные о том, какой уровень воды в метра, на какой угол поворачивается клапан. Однако сам эксперт
знает: высокий уровень воды: примерно 2 метра, интерпретация с помощью нечеткого множества может быть такая:
{(1.5 , 0.1),(1.6 , 0.3),(1.7 , 0.7),(1.8 , 0.8),(1.9 , 0.9),(2 , 1),(2.1 , 1),(2.2 , 1)}Высокий м м м м м м м м
Аналогично можно определить и угол поворота.
Лингвистические переменные представимые числами. И посылка и вывод реализуются с помощью лингвистических
переменных, которые формируются в виде композиции нечетких отношений. Понятие нечеткого отношения является
фундаментальным в теории нечетких множеств.
Нечетким отношением на множества
1 2
, ,...,
n
U U U
называется нечеткое множество R на декартовом произведении
универсумов
1 2
1 2
...
: ... [0,1]
n
R n
U U U
U U U
