Лекции по релятивистской динамике
Подождите немного. Документ загружается.

РЕЛЯТИВИСТСКАЯ ДИНАМИКА
1. Четырехвектор энергия – импульс.
При построении нерелятивистской механики в основу были положены законы Ньютона.
При построении релятивисткой динамики необходимо что-то постулировать. Мы будем
следовать той же логике и начнем со второго закона Ньютона, модифицировав его так, чтобы
его было можно применять для релятивистских частиц. В то же время при малых скоростях
частиц по сравнению со скоростью света он должен переходить в известный нам. Вообще
при получении всех формул релятивисткой динамики мы, прежде всего, будем проверять их
совпадение в предельном случае малых скоростей с известными аналогами механики
Ньютона. Второй основополагающий принцип - полученные уравнения должны быть
инвариантны относительно преобразований Лоренца.
В СТО был введен четырех мерный радиус-вектор, в котором три проекции обычные
проекции на координатные оси трех мерного пространства, четвертая фактически была
временем, умноженная на скорость света для того, чтобы все компоненты были одной
размерности. Чтобы получить релятивистский аналог второго закона Ньютона, надо
«сконструировать» четырех мерный импульс:
(4)
1
1
22
22
(4)
2
2
22
22
(4)
3
3
22
22
4
4
22
22
11
11
11
()
11
x
xx
y
yy
z
zz
mv
dxdx
pmmpp
d
vv
dt
cc
mv
dx dy
pmmpp
d
vv
dt
cc
dx
mvdz
pmmpp
d
vv
dt
cc
dx dctmc
pmm
d
vv
dt
cc
τ
τ
τ
τ
=====
−−
=====
−−
=====
−−
===
−−
(28)
Далее мы будем иметь дело только с релятивистским импульсом, поэтому не имеет смысла
усложнять написание всех формул лишним индексом. Вектор трех мерного импульса будем
обозначать, как и в механике Ньютона:
(4)(4)(4)
xxyyzzxxyyzz
pppppp
=++≡++
peeeeee
(29),
а его модуль как
p
.
Что по существу было сделано. Мы продифференцировали по собственному времени
умноженный на массу интервал (27):
2222
3412
()[()()()]
dxdxdxdxdS
mmmmm
dddddτττττ
=−++ (30),
и получили модуль четырех мерного импульса. Обратите внимание, что под корнем первое
слагаемое четвертая компонента. Логичней было бы дифференцировать модуль радиус-
вектора, умноженного на массу частицы. По этому поводу посмотрите пояснения при выборе
интервала между событиями (к формуле (25)). Важно, что дифференцирование выполнено по
собственному времени. Это необходимо для инвариантности четырех мерного импульса
относительно преобразований Лоренца. Мы уже знаем величину этого инварианта то
согласно (27):
dS
mmc
d
τ
= (31)
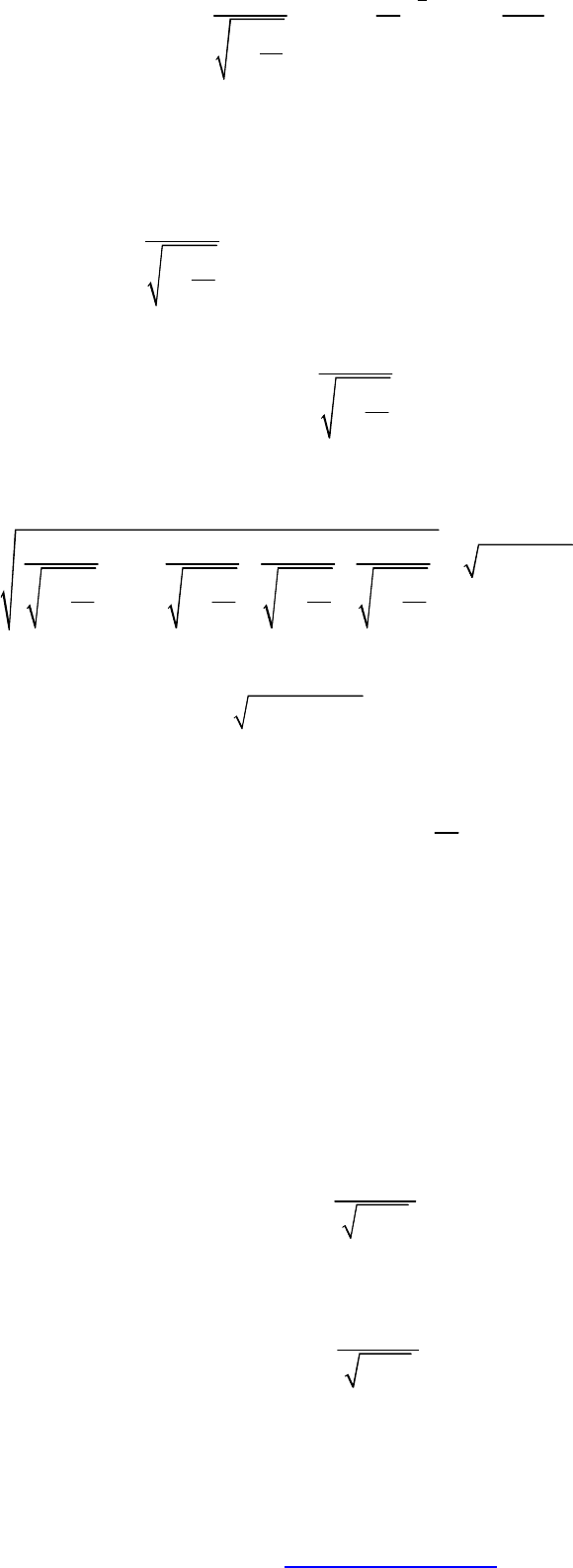
Рассмотрим физический смысл четвертой компоненты (28). Для этого найдем ее значение
при малых скоростях:
PDF created with pdfFactory Pro trial version www.pdffactory.com
1
22
2
4
2
2
2
(1)
2
1
mcvmv
pmcmc
cc
v
c
−
==−=+
−
Из полученного выражения следует, что физический смысл имеет не четвертая компонента
импульса, а произведение
4
p
на скорость света. Тогда это произведение следует назвать
релятивисткой энергией свободной частицы (в отсутствии полей), а величину
2
mc
энергией
покоя:
2
2
2
1
mc
E
v
c
=
−
(32),
2
0
Emc
= (33)
Разность (31) и (32) называют кинетической энергией релятивистской частицы:
2
2
0
2
2
1
k
mc
EEEmc
v
c
=−=−
−
(34)
Если (30) умножить на скорость света, то произведение останется инвариантным
относительно преобразований Лоренца. Этот инвариант получил название энергия-импульса.
Его значение во всех системах отсчета равно:
2
222222
2222
2222
()[]
1111
xxx
mvmvmvmc
cEpcmc
vvvv
cccc
−++=−=
−−−−
(35)
Выпишем еще раз очень важное соотношение, связывающее релятивистскую энергию
частицы с ее импульсом и энергией покоя:
2224
Epcmc
=+ (36)
Стоит обратить внимание на то, что во всех формулах
v
- скорость частицы, и она не имеет
никакой связи со скоростью
0
v
, стоящей в релятивистском корне преобразований Лоренца.
Чтобы не возникали ошибки, мы не будем отношение
2
2
v
c
обозначать
2
β
.
2. Преобразование вектора энергия – импульс.
Построение специальной теории относительности (включая релятивистскую динамику) с
переходом в четырех мерное пространство хорошо тем, что мы «бесплатно» получаем
формулы преобразования всех необходимых физических величин при переходах между
движущимися инерциальными системами отсчета, и еще в придачу значения всех
инвариантов, так как их вычисление в системе, в которой частица покоится, не представляет
труда.
Так как в СТО мы назвали четырех мерными векторами объекты, которые преобразуются
так же, как и четырех мерный радиус-вектор, то можно сразу, по подобию с (8), заменив
x
на
p
, написать:
14
1
2
22
33
41
4
2
1
1
pp
p
pp
pp
pp
p
β
β
β
β
′′
+
=
−
′
=
′
=
′′
+
=
−
Введя обычный трех мерный импульс и энергию, получим:
PDF created with pdfFactory Pro trial version www.pdffactory.com
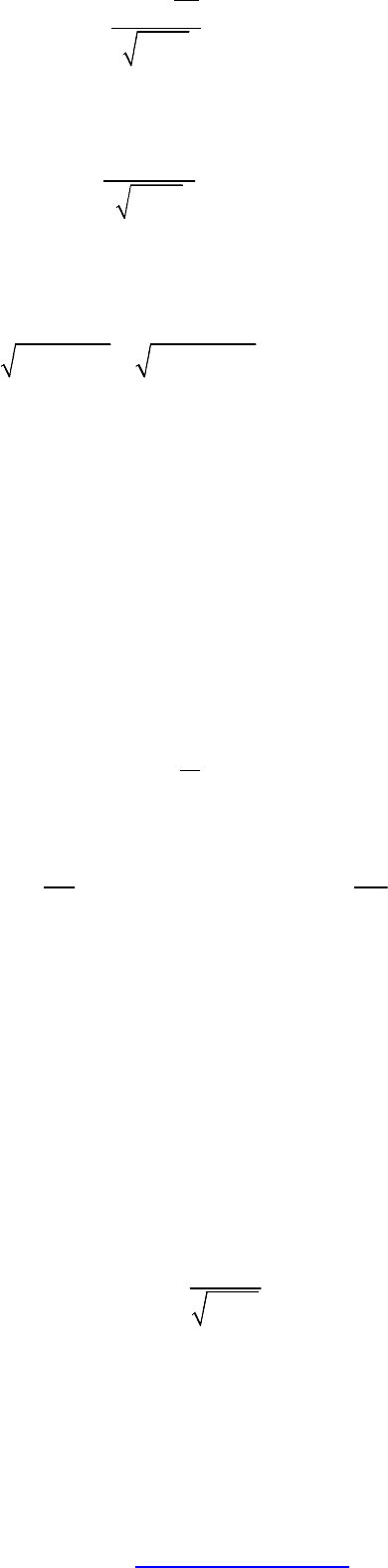
2
2
1
1
x
x
yy
zz
x
E
p
c
p
pp
pp
Epc
E
β
β
β
β
′
′
+
=
−
′
=
′
=
′′
+
=
−
(37),
где β =.v
o
/c, v
o
– скорость движущейся системы относительно той, которую мы считаем
неподвижной.
Полученное выше соотношение между энергией и импульсом частицы (35) в силу его
инвариантности можно записать в виде равенства:
222222
EpcEpc
′′
−=− (38),
которое часто используется при решении задач на столкновении частиц или их
превращениях. Одну такую задачу мы рассмотрим после того, как рассмотрим систему,
состоящую из нескольких частиц.
3. Частицы с нулевой массой. Фотоны.
При скорости частицы равной скорости света знаменатель выражения для релятивистской
энергии (32) обращается в нуль, а энергия становится бесконечно большой, что физически не
имеет смысла. Чтобы энергия была конечной из математики следует, что числитель дроби
так же должен быть в этом случае равен нулю. Из этого вытекает, что частицы, которые
двигаются со скоростью света, должны не иметь массы. И второе, частицы, не имеющие
массы, могут двигаться только со скоростью света, ибо в противном случае ее энергия
обратится в нуль, что физически означает гибель частицы.
Приравняв (35) нулю, мы можем найти связь между энергией и импульсом такой частицы:
E
Epcp
c
=⇒=
(39)
Одна из таких частиц вам хорошо известна – это фотон. Вы также знаете выражения для
энергии и импульса фотона:
2
2
h
Eh
νπνω
π
===
h
(40), p
c
ω
=
h
(41),
где
h
и
h
- постоянная Планка. В последние десятилетии физики перешли в написании
формул на перечеркнутую постоянную Планка, а циклическую
ω
(как она ранее называлась)
стали просто называть частотой. Вектор импульса фотона направлен по направлению
движения. О других частицах с массой равной нулю вы узнаете позже.
Рассмотрим мысленный опыт. Имеются два наблюдателя. Один в неподвижной системе.
Второй в системе движущейся с около световой скоростью. Когда второй наблюдатель
пролетает над другим (их y-вые координаты разные), его источник света делает две
коротких вспышки через очень малое время. То есть можно считать, что обе вспышки
произошли, когда наблюдатели находились на одной прямой, перпендикулярной оси x.
Обозначим интервал времени между вспышками по часам наблюдателя, держащего
источник,
0
T
. По часам наблюдателя, принявшего этот сигнал, интервал времени между
вспышками будет равен согласно (15):
0
2
1
T
T
β
=
−
Конечно, такой опыт сделать невозможно по многим причинам. Но можно сделать
практически аналогичный опыт по физической сути. Можно создать узкий пучок
возбужденных атомов, движущихся с ультрарелятивистскими скоростями, и определить
частоту принятого приемником света от участка пучка, от которого свет распространяется в
перпендикулярном направлении вектору скорости атомов. Естественно, можно померить
частоту света, испущенного покоящимися атомами. Но тогда в предыдущей формуле
PDF created with pdfFactory Pro trial version www.pdffactory.com
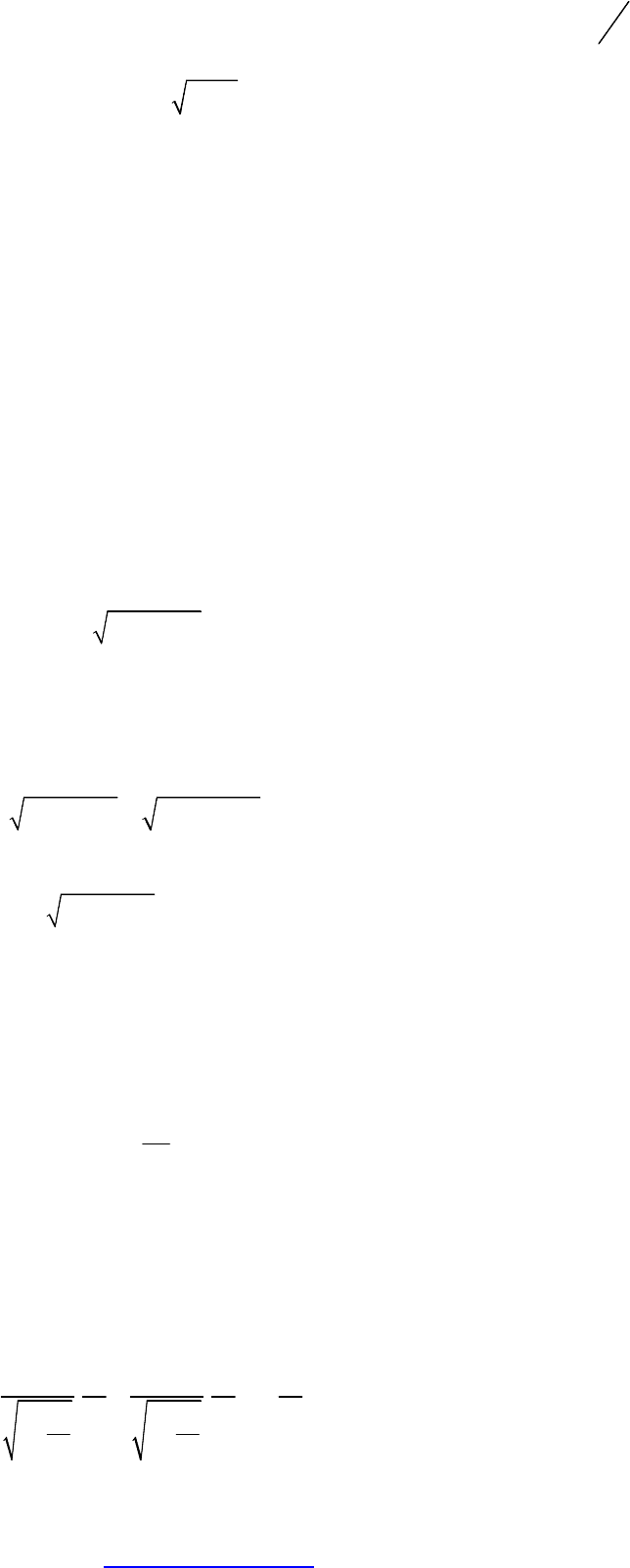
времена для опыта с атомами будут периодами, связанными с частотами формулой
1
i
i
T
ω : .
Таким образом, для частот получим формулу:
2
0
1
β
ωω
=−
И такой опыт был сделан, но из-за технической сложности создания пучка
ультрарелятивистских частиц, чуть более тридцати лет после публикации СТО. По –
научному называя, мы рассмотрели поперечный эффект Доплера, о котором вы узнаете
более подробно в изучения волновой оптики (конец 4–го семестра). Сейчас нам важно, что
прямым опытом подтверждено утверждение, казавшееся фантастичным, что время в
движущихся относительно друг друга системах отсчета течет по-разному.
4. Системы нескольких частиц.
Если система состоит из
N
частиц, то полная энергия системы вводится как сумма энергий
всех частиц:
1
N
i
i
EE
=
=
∑
(42),
а импульс системы как векторная сумма импульсов всех частиц:
1
N
i
i=
∑
p=p
(44)
Если потребовать, чтобы четырех вектор энергии–импульса преобразовывался, как четырех
мерный радиус-вектор, то величина:
222
Epcinv
−=
будет инвариантна относительно преобразований Лоренца. Ее значение в системе отсчета, в
которой суммарный импульс равен нулю (вы знаете, что такая система называется системой
центра масс), называется энергией покоя системы частиц и обозначается
0
E
. В силу
инвариантности значение корня будет одинаково во всех инерциальных системах отсчета,
движущихся относительно друг друга:
222222
EpcEpc
′′
−=− (45)
Формула, связывающая между собой полную энергию системы частиц, суммарный импульс
системы и энергию системы часто применяется при решении задач:
222
0
EpcE
−=
(46).
Следует подчеркнуть, что энергия покоя системы не равна сумме масс частиц, умноженной
на квадрат скорости света. Покажем это для системы из двух частиц. Полная энергия
системы может быть представлена в виде суммы кинетической энергий и энергий покоя двух
частиц, причем полная энергия в системе центра масс равна
0
E
. Таким Образом:
22
11220
ETmcTmcE
=+++=
перегруппировав члены, получим:
2
0
1212
2
[()]0
E
TTcmm
c
+=−+>
Если частицы не покоятся, то из последней формулы хорошо видно, что энергия покоя не
равна суммарной массе частиц, умноженной на квадрат скорости света, и тем больше ее, чем
больше кинетическая энергия частиц. Между прочим, из этого вытекает, что при нагреве
тела оно должно становиться тяжелее, так как растет кинетическая энергия атомов или
молекул, из которых состоит тело. Но этот эффект настолько мал, что наблюдать его нельзя.
Давайте, в качестве упражнения, найдем скорость центра масс двух частиц. Для этого
запишем релятивистский импульс в другом виде (полезная формула вообще):
22
222
22
22
11
mcmc
E
ccc
vv
cc
===
−−
gg
vvv
p (47)
Написав (47) для системы частиц, движущейся со скоростью центра масс относительно
неподвижной системы, получим:
PDF created with pdfFactory Pro trial version www.pdffactory.com

12
22
()
cc
EEE
cc
==+
vv
p
Так как суммарный импульс равен сумме импульсов частиц, то, приравняв предыдущее
выражение этой сумме, находим скорость центра масс системы:
2
12
12
()
c
c
EE
+
=
+
pp
v
(48)
5. Законы сохранения.
Начну с истории давних лет. Когда начинал читать лекции, то меня мучил вопрос: почему
из инвариантности (другими словами, сохранения) модуля четырех вектора энергия-импульс
следует сохранение энергии и импульса по отдельности. И я спросил об этом физика-
теоретика, начавшего читать лекции на кафедре теорфизики на десяток лет раньше меня.
Получил ответ: очень просто, если сохраняются вектора, то должны сохраняться и их
проекции. И я такой радостный пошел дальше. К сожалению это неверно. Можно придумать
сколько угодно векторов, имеющих одинаковый модуль, но имеющие разные проекции. В
механике Ньютона мы постулировали Второй закон Ньютона и из него выводили законы
сохранения. Но там же было сказано, что законы сохранения следуют из свойств
пространства и имеют место в физических явлениях, для описания которых механика
Ньютона не применима, но этот вывод выходит за рамки курса общей физики. Что
изменилось, если мы перешли к описанию физических законов для релятивистских частиц?
Перестала быть пригодна механика Ньютона. Но с пространством от этого ничего не
произошло. Но значит и законы сохранения должны продолжать действовать. Никаких
математических доказательств вам знать не надо.
В химии применяют закон сохранения суммарной массы вещества до реакции, и после
реакции. Покажем, что этот закон приближенный и в случае взаимодействия элементарных
частиц в общем случае не выполняется. Самым простым примером является аннигиляция
покоящихся электрона и позитрона. Позитрон отличается от электрона тем, что имеет такой
же заряд, но противоположного знака. Массы их одинаковы. Реакция анигиляции выглядит
так:
2
eе
γ
−+
+→,
букввой
γ
мы обозначили фотон очень большой, называемые гамма-квантами. Их
обязательно должно получиться два, летящих в противоположные стороны, чтобы
суммарный импульс остался равным нулю. Напишем закон сохранения для этой реакции, из
которого можно определить частоту гамма-кванта:
2
22
2
mc
mcmc ωω+=⇒=h
h
В приведенном процессе вообще вся масса перешла в энергию. В реакторах при делении
урана получаются атомы, суммарная масса меньше массы урана. За счет этого и получается
энергия, которую, в конечном счете, переводят в электроэнергию. Но это мы забежали в
материал последнего семестра. При химических реакциях также масса не сохраняется, но ее
изменение не наблюдаемо из-за малости величины. Поэтому химики закон сохранения массы
могут использовать, а физикам надо знать, что он приближенный.
6. Сила. Уравнение движения.
Как двигаться дальше, должно быть понятно из предыдущего вывода четырех мерного
импульса. Чтобы получить релятивистский аналог Второго закона Ньютона, его надо
продифференцировать по времени Для трех пространственных координат будем иметь:
2
(4)(4)
2
1
iii
iii
dpdpdpv
FFF
ddtcdtτ
=⇒=−⇒=
(1,2,3)
i
=
В последнем равенстве стоит проекция обычной трех мерной силы. В противном случае
выражение при малых скоростях не будет переходить в нерелятивистский Второй закон
Ньютона. Уравнение движения для релятивистских частиц можно записать в векторном
виде:
PDF created with pdfFactory Pro trial version www.pdffactory.com
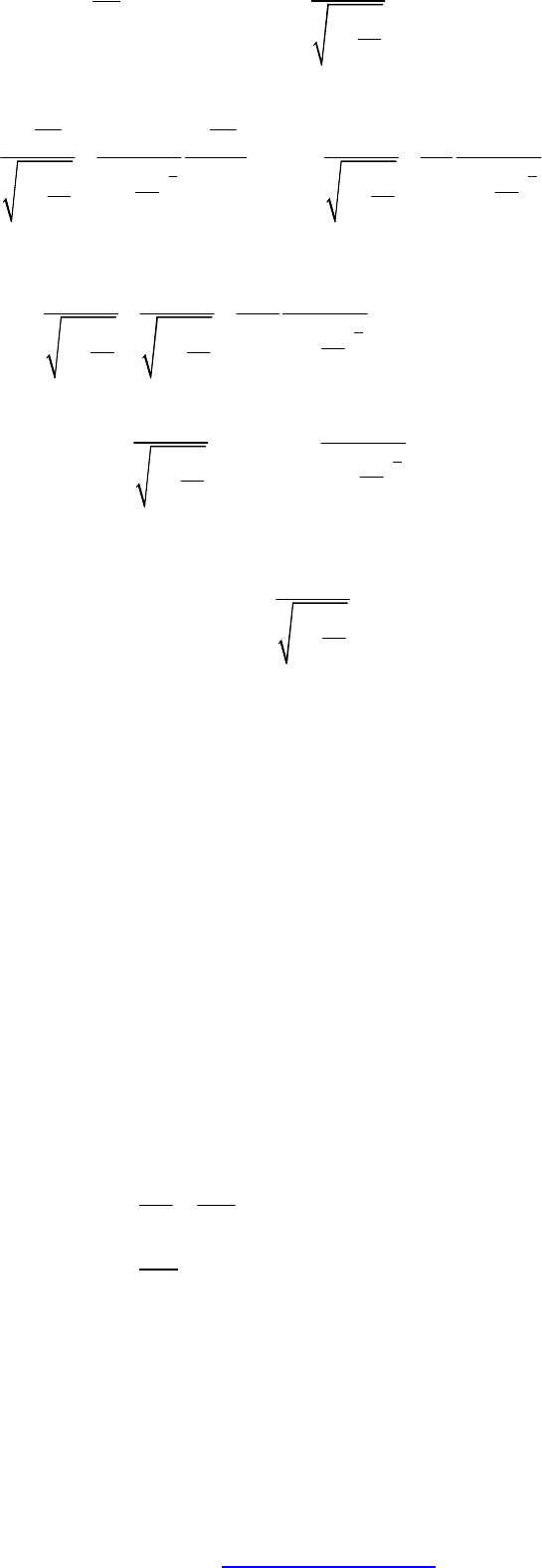
d
dt
=
p
F
, где
2
2
1
m
v
c
−
v
p=
(49)
Продифференцируем импульс, чтобы получить ускорение:
33
22
22
22
22
22
22
()
()
(1)(1)
11
dd
m
mmm
dtdt
cc
vv
vv
cc
cc
+=⇒+=
−−
−−
vv
v
vavva
FF
Разложим вектор ускорения на тангенциальную (направленную по направлению скорости) и
нормальную составляющие (перпендикулярную скорости):
3
2
2
22
2
2
22
(1)
11
n
n
mamava
mv
FF
c
v
vv
c
cc
ττ
τ
++=+
−
−−
n
n
τ
τ
τ
(50)
Запишем это векторное уравнение в проекциях:
2
2
1
n
n
ma
F
v
c
=
−
3
2
2
2
(1)
ma
F
v
c
τ
τ
=
−
Второе уравнение получается при суммировании двух членов в (50). В некоторых учебниках
водится масса покоя и масса движущейся частицы как:
0
2
2
1
m
m
v
c
=
−
Из двух предыдущих уравнений хорошо видно, что если и заниматься такой абракадаброй,
то следует вводить две массы движения: одну «продольную», а вторую «поперечную». Так
что советую последнею формулу забыть. Она пережиток прошлого.
7. Примеры решения задач по СТО и РЕЛЯТИВИСТСКОЙ ДИНАМИКЕ
Эффект Комптона.
Эффектом Комптона называют рассеяние гамма-кванта (фотона большой энергии) на
свободном электроне. Если перевести на наш язык первого семестра, то под рассеянием
следует понимать абсолютно упругое столкновение фотона с электроном. Задача решается с
помощью законов сохранения энергии и импульса для замкнутой системы двух частиц. Мы
предполагаем, что энергия
γ
- кванта так велика, что для энергии электрона надо
использовать релятивистскую формулу для энергии. Естественно, что до столкновения
электрон имел энергию покоя. Уравнение, выражающее закон сохранения энергии для
системы имеет вид:
2
mcE
ωω
′
+=+
hh
(1)
Закон сохранения импульса напишем в проекциях на оси: совпадающую с первоначальным
направлением движения - кванта и перпендикулярную ей:
coscos
sinsin
p
cc
p
c
ωω
αβ
ω
αβ
′
=+
′
=
hh
h
(2)
,
αβ
−
углы рассеяния (отсчитываемые от оси, совпадающей с первичным направлением
фотона) - кванта и электрона соответственно. Уравнения три, а входящих величин больше.
Поэтому определимся с тем, что измеряется на опыте, а что подлежит вычислению. Мы
будем считать известными величинами: частоту или энергию кванта до рассеяния и угол, на
который он рассеялся. Кроме того, нам известна формула, связывающая между собой
энергию, импульс и энергию электрона. Задача – вычислить энергию
γ
- кванта после
столкновения с электроном.
PDF created with pdfFactory Pro trial version www.pdffactory.com

Исключим (2) угол рассеяния электрона. Для этого сложим квадрат правой части второго
уравнения с квадратом первого после переноса импульса рассеянного фотона в левую часть:
222
(cos)(sin)
p
ccc
ωωω
αα
′′
−+=
hhh
После тривиальных преобразований получим:
22222222
()()2cos()
pcEmc
ωωωωα
′′
+−==−
hhh
(3)
Найдем из (1) квадрат энергии электрона и приравняем его с выраженным из (30):
222222
22222
()()22()()
()()2cos()
mcmc
mc
ωωωωωω
ωωωωα
′′′
+−+−+=
′′
=+−+
hhhhh
hhh
Исключив подобные члены, получим:
22
()(1cos)
mc
ωωωωα
′′
−=−
hhh
Поделим последнее равенство на
2
mc
ωω
′
h
:
2
11
(1cos)
mc
α
ωω
−=−
′
h
Так как длина волны связана с частотой, как
2
π
λ
ω
= , последнюю формулу можно записать
через разность длин волн:
2
2
(1cos)
mc
π
λλα
′
−=−
h
(4)
Экспериментально можно определить изменение длины в зависимости от угла рассеяния.
Как это делается, будет объяснено в пятом семестре. Решение этой задачи здесь приведено
по двум причинам. Во–первых, совпадение опыта с расчетом подтверждает выше
рассмотренную теорию. Во–вторых, показать на примере, как записываются законы
сохранения для релятивистских частиц.
Задача приведена, чтобы нее примере показать, как применяются законы сохранения.
Рождение частицы.
Имеется покоящаяся частица массы
M
. Какой минимальной кинетической энергией
должна обладать частица массы
m
, чтобы при столкновении родилась еще одна такая же
частица?
Задачи такого типа делаются с использованием инварианта энергия–импульса. Для
налетающей частицы из него находится связь между ее полной энергией, импульсом и
энергией покоя:
22222
()
pcmc
ε −= (1)
Напишем этот инвариант для системы двух частиц до столкновения:
22222222
0
()
EPcMcpcE
ε−=+−= (2)
В системе центра масс величина инварианта не изменится:
22
00
C
EE
=
После столкновения величина инварианта снова не изменится:
22
00
CC
EE
′
=
Минимальной кинетическая энергия (конечно, и полная) будет в том случае, когда после
столкновения все частицы в системе центра масс будут покояться. В этом случае полная
энергия трех частиц будет равна :
22
0
2
CC
EmcMcE
′′
=+=
Используя все написанные равенства, получим:
2222222
()(2)
McpcmcMc
ε +−=+
Возведя в квадраты и заменяя импульс налетающей частицы из (1) находим выражение, из
которого можно найти минимальную полную энергию налетающей частицы:
2222222222222
2()()4()4()
McMcmcmcmcMcMc
εεε++−+=++
Приведя подобные члены, получим:
PDF created with pdfFactory Pro trial version www.pdffactory.com

2
2222222
2
3
23()42
2
mc
McmcmcMcmcmc
Mc
εε=+⇒=+
Искомая кинетическая энергия равна найденной полной энергии за вычетом энергии покоя:
2
min
3
(1)
2
m
Tmc
M
=+.
На примере этой задачи хотел показать, как надо пользоваться инвариантами.
PDF created with pdfFactory Pro trial version www.pdffactory.com
