Лекции по гидравлике

Подождите немного. Документ загружается.

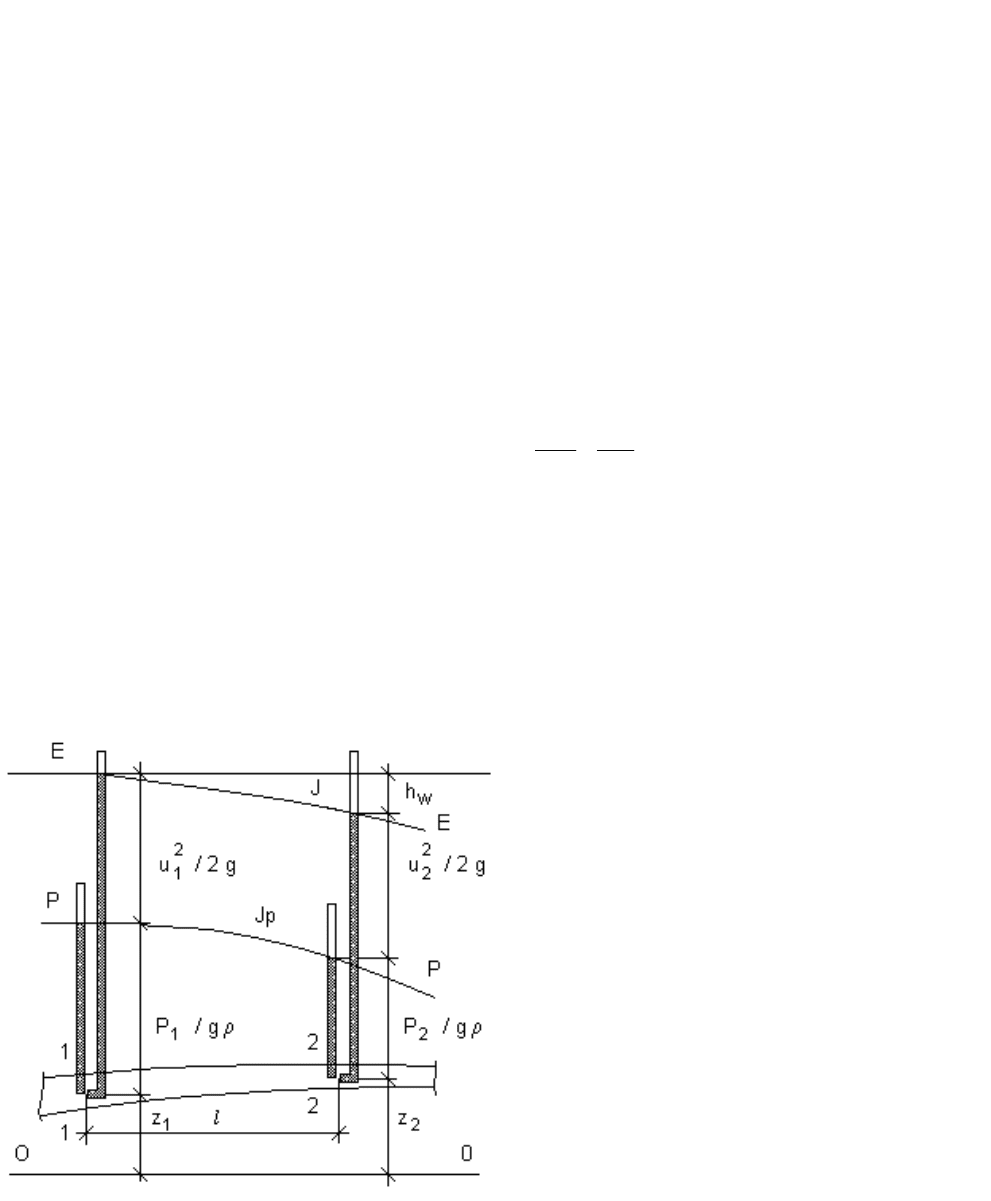
рис. 1.16

Как видно, все члены в уравнении Бернулли представляют собой геометрические

высоты и имеют размерность длины.

Так как сумма трех членов

)/( pgP

, z и

)2/(

для идеальной жидкости постоянна

вдоль оси струйки, то уровни жидкости в трубках Пито, установленных в

различных сечениях будут всегда лежать в одной горизонтальной плоскости,

называемой напорной плоскостью, т.е. напорная линия E - E (рис. 2)

горизонтальна. В этом состоит геометрический смысл уравнения Бернулли для

идеальной жидкости.

Если плавной кривой соединим уровни жидкости в пьезометрах, то получим

пьезометрическую линию P - P (рис. 2), которая может подниматься или

опускаться, но никогда не пересекается с напорной линией.

Сумма трех высот называется полным напором и обозначается Н

, т.е. полный

напор представляет собой сумму пьезометрического

zgPzhH

 )/(



скоростного

)2/(

guh



напоров:











(1.39)

С энергетической точки зрения уравнение Бернулли выражает закон сохранения

энергии. Полный напор

- это полная удельная механическая энергия жидкости

в рассматриваемом сечении. Сумма трех членов есть сумма трех удельных

энергий: удельной потенциальной энергии давления

)/( gP



, удельной

потенциальной энергии положения z, удельной кинетической энергии

)2/(

Для идеальной жидкости сумма трех удельных энергий (полный напор) по длине

струйки есть величина постоянная.

Рис.1.17

Реальная жидкость, в отличии от идеальной, обладает вязкостью. При движении

реальной жидкости ее вязкость обуславливает сопротивление движению и

вызывает потерю части энергии, поэтому полный напор уменьшается по длине

струйки. Следовательно, уровни жидкости в трубках Пито будут снижаться по

ходу движения. Напорная линия Е - Е, проведенная по этим уровням для вязкой

жидкости, будет наклонной, нисходящей. Разность между горизонтальными

линиями Е - Е, проведенными на уровне жидкости в трубках Пито в сечениях 1 - 1

и 2 - 2, представляет потери напора

на участке между этими сечениями (рис.

1.17).

Таким образом, для реальной жидкости можно записать

hHH 

(1.40)

Или в развернутом виде







(1.41)

Потери напора, отнесенные к единице длины, выражают величину, которая

называется гидравлическим уклоном:

































(1.42)

где I - гидравлический уклон; l - расстояние между сечениями 1 - 1 и 2 - 2.

Величина гидравлического уклона вдоль струйки может изменяться, так как

зависит от потерь напора на различных участках.

Изменение пьезометрического напора, отнесенное к единице длины, называется

пьезометрическим уклоном.

































(1.43)

где I

- пьезометрический уклон; l - расстояние между сечениями 1 - 1 и 2 - 2.

Пьезометрический уклон может быть направлен как в сторону движения, так и в

сторону, противоположную движению.

Для потока реальной жидкости уравнение Бернулли имеет вид















(1.44)

где v

и v

- средние скорости движения жидкости в рассматриваемых сечениях;

- коэффициенты кинетической энергии, величина которых зависит от

степени неравномерности распределения скоростей по живому сечению потока.

Коэффициент выражает отношение действительной кинетической энергии K

определенной по истинным скоростям движения жидкости, к условной

кинетической энергии K

, определенной по средней скорости потока v:











(1.45)

При турбулентном режиме движения

принимается равным 1,05- 1,1. При

ламинарном режиме

2a

1.5 Потери напора при установившемся движении.

Влияние различных факторов на движение жидкости

Кинематика жидкости существенно отличается от кинематики твёрдого тела.

Если отдельные частицы абсолютно твёрдого тела жёстко связаны между собой,

то в движущейся жидкой среде такие связи отсутствуют; эта среда состоит из

множества частиц, движущихся одна относительно другой.

Скорость в данной точке пространства, занятого движущейся жидкостью,

является функцией координат этой точки, а иногда и времени.

Рассмотрим движение идеальной жидкости, т.е. такой воображаемой жидкости,

которая совершенно лишена вязкости. В такой не вязкой жидкости, так же как и в

неподвижных реальных жидкостях, возможен лишь один вид напряжений -

нормальные напряжения сжатия, т.е. гидромеханическое давление, или просто

давление.

Давление в движущейся идеальной жидкости обладает теми же свойствами, что

и в неподвижной жидкости, т.е. на внешней поверхности жидкости оно

направлено по внутренней нормали, а в любой точке жидкости - по всем

направлениям одинаково.

Течение жидкости может быть установившемся (стационарным) и

неустановившемся (нестационарным).

Установившемся называется течение жидкости, неизменное по времени, при

котором давление и скорость являются функциями только координат, но не

зависят от времени. Давление и скорость могут изменяться при перемещении

частицы жидкости из одного положения в другое, но в данной неподвижной

относительно русла точке давление и скорость при установившемся движении не

изменяются по времени, т.е.:

),,(

zyxfp 

);,,(

zyxfv 

(1.46)

;0



;0



;0



;0



(1.47)

где индексы у скорости означают её проекции на соответствующие оси,

жёстко связанные с руслом.

Неустановившемся движением называется движение у которого все

характеристики изменяются по времени в точках рассматриваемого характера.

При неустановившемся течение траектории различных частиц, проходящих

через данную точку пространства, могут иметь разную форму. Поэтому для

рассмотрения картины течения, возникающей в каждый данный момент времени,

вводится понятие линии тока.

Линией тока называется кривая, в каждой точке которой вектор скорости в

данный момент времени направлен по касательной.

Если в движущейся жидкости взять бесконечно малый замкнутый контур и

через все его точки провести линии тока, то образуется трубчатая поверхность,

называемая трубкой тока. Часть потока, заключённая внутри трубки тока,

называется элементарной струйкой.

Живым сечением, или просто сечением потока, называется в общем случае

поверхность в переделах потока, проведённая нормально к линиям тока. Далее

будем рассматривать в потоках такие участки, в которых струйки можно считать

параллельными и, следовательно, живые сечения - плоскими.

Различают напорные и безнапорные течения жидкости. Напорными называют

течения в закрытых руслах без свободной поверхности, а безнапорными - течения

со свободной поверхностью. При напорных течениях давление вдоль потока

обычно переменное, при безнапорном - постоянное (на свободной поверхности) и

чаще всего атмосферное.

Понятие о подобных потоках и критериях подобия

Установление зависимости интересующей величины от системы выбранных

определяющих факторов может выполняться двумя путями: аналитическим,

основанным на законах механики и физики, и экспериментальным. Первый путь

применим лишь для ограниченного числа задач и при том обычно лишь для

упрощённых моделей явлений.

Другой путь, экспериментальный, в принципе может учесть многие факторы,

но он требует научно обоснованной постановки опытов, планирования

эксперимента, ограничения его объёма необходимым минимумом и

систематизацией результатов опытов. При этом должно быть обосновано

моделирование явлений.

Эти задачи позволяет решать так называемая теория гидродинамического

подобия, т.е. подобия потоков несжимаемой жидкости.

Гидродинамическое подобие складывается из трёх составляющих:

геометрического подобия, кинематического и динамического.

Геометрическое подобие представляет собой пропорциональность

сходственных размеров и равенство соответствующих углов. В гидравлике под

геометрическим подобием понимают подобие тех поверхностей, которые

ограничивают потоки, т.е. подобие русел (или каналов).

Кинематическое подобие означает пропорциональность местных скоростей в

сходственных точках и равенство углов, характеризующих направление этих

скоростей. Из кинематического подобия вытекает геометрическое подобие линий

тока. Очевидно, что для кинематического подобия требуется геометрическое

подобие русел.

Динамическое подобие - это пропорциональность сил, действующих на

сходственные объёмы в кинематически подобных потоках и равенство углов,

характеризующих направление этих сил.

Числа Рейнольдса, Фруда, Эйлера, Вебера

Совокупность параметров, определяющих какой-либо гидродинамический

процесс, можно рассматривать как конкретное решение дифференциальных

уравнений этого процесса. Ему соответствуют вполне определённые начальные и

граничные условия. Они представляют собой зависимости или константы,

определяющие физические параметры в начальный момент и на границах во

время движения. Следовательно, не только уравнения процесса, но также

безразмерные формы начальных и граничных условий (условий однозначности) в

механически подобных потоках должны быть одинаковыми. Имея это в виду,

запишем уравнения Навье-Стокса и приведём их к безразмерному виду, для чего

выберем характерные физические параметры L, V, T, P, F0 (если F - cила тяжести,

то в качестве F0 удобно взять ускорение g свободного падения) и отнесём к ним

соответствующие размерные величины:

;/ Lxx 

;/ Lyy 

;/ Lzz 

;/Vuu



;/Vuu



;/Vuu



;/ Ppp 

FFF



FFF



FFF



;/Ttt 

Для плотности и вязкости, которые считаем постоянными, характерные

величины не выбираем, так как они сами ими являются. Примем также во

внимание размерность дифференциальных операторов



и grad:

 

;

...





















   



grad



;

Векторное уравнение Навье-Стокса можно представить в виде

.)(

pgrad

FF 









(1.48)

Чтобы придать этому уравнению безразмерный вид, разделим все его члены на

коэффициент

LV /

при конвективном ускорении. Получим

,)(

pgrad











(1.49)

где дифференциальные операции выполняются по безразмерным переменным. В

этом уравнение все члены, включая комбинации характерных параметров,

безразмерны. Для всех динамических подобных потоков оно должно быть

одинаковым, а следовательно, группы потоков были одинаковыми, т.е.

idemVLF 

;)/(

idemVP 



;)/( idemVL 



.)/( idemVTL 

(1.50)

Входящие в условия (1.50) безразмерные комплексы играют роль критериев

подобия и имеют следующие собственные наименования:

FrLFV )/(

- число Фруда;

EuVP )/(



- число Эйлера;

Re/ vVL

- число

Рейнольдса;

ShVTL )/(

- число Струхала.

Понятие о гидравлических сопротивлениях, виды потерь напора (местные и

по длине)

Потери удельной энергии (напора), или, как их часто называют,

гидравлические потери, зависят от формы, размеров русла, скорости течения и

вязкости жидкости, а иногда и от абсолютного давления в ней. Вязкость жидкости,

хотя и является первопричиной всех гидравлических потерь, но далеко не всегда

оказывает существенное влияние на их величину.

Гидравлические потери обычно разделяют на местные потери и потери на

трение по длине.

Местные потери энергии обусловлены так называемыми местными

гидравлическими сопротивлениями (рис 1.18), т.е. местными изменениями формы

и размеры русла, вызывающими деформацию потока. При протекании жидкости

через местные сопротивления изменяется её скорость и обычно возникают

крупные вихри. Последние образуются за местом отрыва потока от стенок и

представляют собой области, в которых частицы жидкости движутся в основном

по замкнутым кривым или близким к ним траекториям.

Местные сопротивления напора определяются по формуле следующим

образом:

),2/(

gVh





(1.51)

или в единицах давления

рис. 1.18 Пример местных гидравлических сопротивлений.

.2/





(1.52)

Выражение (1.5.4) часто называют формулой Вейсбаха. В ней V - средняя по

сечению скорость в трубе, в которой установлено данное местное сопротивление.

Потери на трение по длине - это потери энергии, которые в чистом виде

возникают в прямых трубах постоянного сечения, т.е. при равномерном течении, и

возрастают пропорционально длине трубы. Рассматриваемые потери обусловлены

внутренним трением в жидкости, а потому имеют место не только в шероховатых,

но и в гладких трубах.

Потерю напора на трение можно выразить по общей формуле для

гидравлического потерь, т.е.

).2/(

gVh

тртр





(1.53)

или

тр





(1.54)

Общая формула для потерь напора по длине при установившемся

равномерном движении жидкости. Коэффициент Дарси

Как показывают опыты, во многих, но не во всех случаях гидравлические

потери приблизительно пропорциональны скорости течения жидкости во второй

степени, поэтому в гидравлике принят следующий общий способ выражения

гидравлических потерь полного напора в линейных единицах:

)2/(

gVh

срП





, или в единицах давления (1.55)

.2/

cрПП

Vghp





(1.56)

Такое выражение удобно тем, что включает в себя безразмерный коэффициент

пропорциональности



, называемый коэффициентом потерь Дарси или

коэффициентом сопротивления.

Основное уравнение равномерного движения

Выделим некоторый отсек элементарной струйки (рис. 1.19).

рис. 1.19 Объем элементарной струйки

Во вход в это сечение в единицу времени втекает определённый объём

жидкости, равный

111

FVq 

(1.57)

а через выход вытекает объём равный

222

FVq 

(1.58)

Примем, что жидкость несжимаема и что в ней невозможно образование

незаполненных жидкостью пространств - пустот, т.е. будем считать, что

соблюдается условие сплошности или неразрывности движения. Учитывая, что

форма элементарной струйки с течением времени не изменяется и поперечный

приток в струйку или отток из неё отсутствуют, приходим к выводу, что

элементарные расходы жидкости, проходящие через вход и выход данного отрезка

должны быть одинаковы. Таким образом,

qq 

(1.59)

2211

FVFV 

(1.60)

Подобные соотношения можно составить для любых отсеков элементарной

струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки

constFVq 

(1.61)

Полученное уравнение называется уравнением неразрывности; оно является

первым основным уравнением гидродинамики.

Касательные напряжения. Обобщённый закон Ньютона

Согласно гипотезе, высказанной впервые Ньютоном в 1686 г., а затем

экспериментально обоснованной проф. Н.П. Петровым в 1883 г., касательное

напряжение в жидкости зависит от её рода и характера течения и при слоистом

течении изменяется прямо пропорционально ьак называемому поперечному

градиенту скорости. Таким образом





(1.62)

где



-коэффициент пропорциональности, получивший название динамической

вязкости жидкости;

-приращение скорости, соответствующее приращению

координаты

Поперечный градиент скорости

определяет изменение скорости, приходящееся

на единицу длины в направлении нормали к стенке и, следовательно, характеризует

интенсивность сдвига жидкости в данной точке (точнее

-это модуль градиента

скорости; сам градиент – вектор).

Ламинарный и турбулентный режимы движения жидкости. Критическое

число Рейнольдса

Опыты показывают, что возможны два режима или два вида течения

жидкостей и газов в трубах: ламинарный и турбулентный.

Ламинарным называется слоистое течение без перемешивания частиц

жидкости и без пульсаций скоростей и давления. При таком течении все линии

тока определяются формой русла, по которому течёт жидкость. При ламинарном

течении жидкости в прямой трубе постоянного течения все линии тока

направлены параллельно оси трубы, т.е. прямолинейно; отсутствуют поперечные

перемещения жидкости.

Турбулентным называется течение, сопровождающееся интенсивным

перемешиванием жидкости и пульсациями скоростей и давлений. ёДвижение

отдельных частиц оказывается подобным хаотическому, беспорядочному

движению молекул газа. При турбулентном течении векторы скоростей имеют не

только осевые, но и нормальные к оси русла составляющие, поэтому наряду с

основным продольным перемещением жидкости вдоль русла происходят

поперечные перемещения (перемешивание) и вращательное движение отдельных

объёмов жидкости. Этим и объясняются пульсации скоростей и давления.

Режим течения данной жидкости изменяется в данной трубе примерно при

определённой средней по сечению скорости течения Vкр, которую называют

критической. Как показывают опыты, значение этой скорости прямо

пропорционально кинематической вязкости

и обратно пропорционально

диаметру d трубы, т.е.

dkvV

кр

/

(1.63)

Входящий в эту формулу безразмерный коэффициент пропорциональности

одинаков для всех жидкостей и газов, а также для любых параметров труб. Это

означает, что изменение режима течения происходит при определённом

соотношении между скоростью, диаметром и вязкостью

vdVk

кр

/

(1.64)

Этот результат согласуется с изложенной выше теорией гидродинамического

подобия, и вполне закономерно, что именно число Рейнольдса является

критерием, определяющим режим течения в трубах.

Как показывают опыты, для труб круглого сечения

2300Re 

кр

Таким образом, критерий подобия Рейнольдса позволяет судить о режиме

течения жидкости в трубе. При

кр

ReRe 

течение является ламинарным, при

кр

ReRe 

- турбулентным.

Смена режима течения обусловлена тем, что одно течение при достижении

критического числа Рейнольдса теряет устойчивость, а другое - приобретает.

Пульсации скоростей при турбулентном режиме. Мгновенная и местная

осреднённые скорости

Как было сказано в предыдущем пункте, для турбулентного течения

характерны перемешивание жидкости пульсации скоростей и давлений.

Скорость постоянно колеблется около осреднённого

оср

по времени

значения. Траектории частиц, проходящих через данную неподвижную точку

пространства в разные моменты времени, представляют собой кривые линии

различной формы, несмотря на прямолинейность трубы. Таким образом,

турбулентное течение всегда является неустановившемся, так как значения

скоростей и давлений, а также траектории частиц, изменяются по времени.

Однако его можно рассматривать как установившееся течение при условии, что

осреднённые по времени значения скоростей и давлений, а также полный расход

потока не изменяются со временем.

Распределение скоростей (осреднённых по времени) в поперечном сечении

турбулентного потока существенно отличается от того, которое характерно для

ламинарного течения. Если сравним кривые распределения скоростей в

ламинарном и турбулентном потоках в одной и той же трубе и при одном и том

же расходе (одинаковой средней скорости), то обнаружим существенное

различие. Распределение скоростей при турбулентном течении более равномерно,

а нарастание скорости у стенки более крутое, чем при ламинарном течении, для

которого характерен параболический закон распределения скоростей.

В связи с этим, коэффициент Кориолиса



, учитывающий неравномерность

распределения скоростей в уравнении Бернулли при турбулентном течении,

значительно меньше, нежели при ламинарном.

Потери напора по длине при равномерном ламинарном движении жидкости

При ламинарном течении потеря напора на трение по длине при ламинарном

течении пропорциональна скорости в первой степени [квадрат скорости в

формуле (1.6.6) для ламинарного течения получен искусственно умножением и

делением на

ср

], а коэффициент



обратно пропорционален Re и,

следовательно, скорости

ср

cр

лТР





, (1.65)

где



- коэффициент потерь на трение для ламинарного течения:





(1.66)

Распределение скоростей по живому сечению в цилиндрической трубе при

ламинарном режиме. Коэффициент Дарси при ламинарном течении

Если боковая поверхность трубы есть поверхность цилиндра, то естественно

допустить существование ламинарного течения с линиями тока в виде прямых,

параллельных образующим цилиндра.

Для отыскания скорости имеем уравнение Пуассона с постоянной правой

частью













(1.67)

граничным условием которого является равенство нулю скорости не стенке

трубы.

В общем случае рассматриваемое течение может быть обусловлено как

перепадом давления

p

, так и осевым движением одного из цилиндров (речь