Лекции по гидравлике в виде шпор

Подождите немного. Документ загружается.

Лекция 1

Гидромеханика изучает законы движения жид-

ти, газов. Разделяется на статику, кинематику и

динамику.

Гидростатика…

Кинематика изучает и движение во времени, не

интересуясь причинами, вызывающими движение.

Гидродинамика изучает движение жид-ти и

газов при взаимодействии с твердыми телами.

Гидравлика является прикладной инженерной

наукой основанной в основном на экспериментальных

данных.

Жид-ти и газы обладают двумя основными св-

вами сплошностью и текучестью.

Гидромеханика не занимается изучением

отдельных молекул, а исходит из допущения, что всё

пространство непрерывно заполнено вещ-вом.

Условия сплошности выполняются, если

характерные линейные размеры в области течения и

реки по сравнению с длиной свободного пробега

молекул.

Текучесть позволяет ввести понятия вязкости

как свойство жид-ти и газов оказывает сопротивление

при перемещении.

Текучесть величина обратная вязкости.

Гидравлика и гидродинамика изучает законы

движения Ньютоновской жид-ти, для которых

напряжение, вызываемое вязкостью, выражается

равномерно через скорость деформации. Для не

Ньютоновской жид-ти движение зависимости

значительно сложнее, законы их движения изучает

реология.

В жид-тях и газах любая сколь угодно малая

касательная сила вызывает смещение одного слоя

относительно другого. В гидродинамике часто

пользуются понятием идеальной жид-ти, коэффициент

вязкости = 0, это возможно когда коэффициентом

вязкости можно пренебречь.

Гидравлика и гидродинамика имеют большое…

1. Плотность и сжимаемость.

Для характеристики распределения массы в

пространстве занятой жид-тью или газом пользуются

величиной называемой плотностью.

Среднее значение плотности:







∆m-масса; ∆V-объем;

Значение ρ в данной точке:





 0

lim



[кг/м

]

Величина обратная плотности наз-ся удельным

объемом:







[м

/кг]

Плотность зависит от p, t: ρ=g(x, y, z, t)

В технике часто пользуются понятием

удельного веса (γ).







 g



[Н/м

]

Способность жид-ти и газа изменять свою

плотность или объем под действием внешнего давления

называется сжимаемостью. Количественно она

определяется сжимаемой плотностью к единице

приложенного джавления. Обратная величина:







Для малосжимаемой жид-ти при больших

изменениях ∆ρ, а скорость звука большая. Скорость

звука служит характеристикой сжимаемости в

состоянии покоя. Для воды скорость звука составляет

≈1500 м/с, для воздуха >300 м/с.

Если жидкость или газ движутся, то для их

оценки используют не скорость звука, а отношение

M 

, которое называется числом

Маха.

Если число Маха мало М<<1, то жид-ть (газ)

можно считать несжимаемым, при больших скоростях

сжимаемость влияет на характер…

2. Законы переноса

В отличие от идеальных жид-тей (газов) у

которых … = 0, и отсутствует перенос массы и тепла в

реальных вязких жид-тях … переноса тепла и массы

(т.е. диффузии). Они происходят как в покоящихся … и

является средсьвом проявления сил вязкости.

Если в потоке или в объеме выделить

элементарный объем, то на него будут действовать

нормальные и касательные силы.

Касательные силы возникают вследствие

вязкости.

Ньютон: касательное напряжение м/у слоями жид-ти

(газа) пропорциональны отнесенному к единице длины

… по нормали к направлению движения.







[µ]=Н*сек/м

– коэф.

динамической вязкости

Из уравнения видно, что когда скорость

нормальная не изменяется, перенос движения

отсутствует.

µ не зависит от p и от характера движения, а

зависит от физ. св-тв жид-ти и от темп-ры.

Наряду с ним часто используют









[м

/сек] – коэф. кинетической

вязкости

Для жид-ти с ростом темп-ры вязкость

уменьшается, для газов увеличивается.

Законы переноса тепла и массы имеют вид

аналогичный закону Ньютона.

Перенос тепла характеризуется законом Фурье







, а перенос веществ

законом Фика





где q и m – количество тепла и вещества переносимого

через единицу площади за единицу времени;

T и c – температура и концентрация вещества

λ и D – коэффициент теплопроводности и диффузии

Структура потоков. Турбулентность.

По структуре все существующие потоки в

реальной вязкой жид-ти делятся на ламинарное и

турбулентное.

При ламинарном (слоистом) движении

отдельные частицы движутся по траекториям.

При турбулентном движении отдельные

частицы совершают беспорядочное движение по

хаотически и быстроменяющимся траекториям.

От структуры потока существенно зависят

величины характеризующие перенос количества

движения, тепла, вещества. Законы переноса

справедливы только при ламинарном потоке, при

турбулентном они сложнее.

Наиболее распространённым является

турбулентное движение. Оно сопровождается

интенсивным перевешиванием частиц → выравнивание

… происходит в более короткие сроки.

Сопротивление жид-ти движению тела при

наличии … в одних случаях увеличивается в других

уменьшается.

Величиной определяющей является число

Рейнольдса



Re

ν – кинематическая вязкость

Переход от ламинарного движения к

турбулентному происходит при числе Рейнольдса

называемой критической.

Для гладких прямолинейных труб Re

кр

=2300

В других случаях число Re определяется

экспериментально.

Основы гидростатики.

1. Силы, действующие в жидкости.

Гидростатическое давление.

Силы: внутренние и внешние.

По своему характеру силы делятся на массовые

или объемные и поверхностные.

Поверхностные силы складываются из

поверхностных сил … к выд площадке по касательной.

В покоящейся жидкости сила действует только

по нормали.

Обычно рассматривают не поверхностные

силы, а их напряжение. Для измерения давления

используются следующие величины [Н/м

]=Па

На практике часто пользуются техн. атм.

1 атм = 736 мм рт ст = 10 м вод ст

][

80665,9

][

5,98066

222

кг

см

кг



1 бар = 10

Н/м

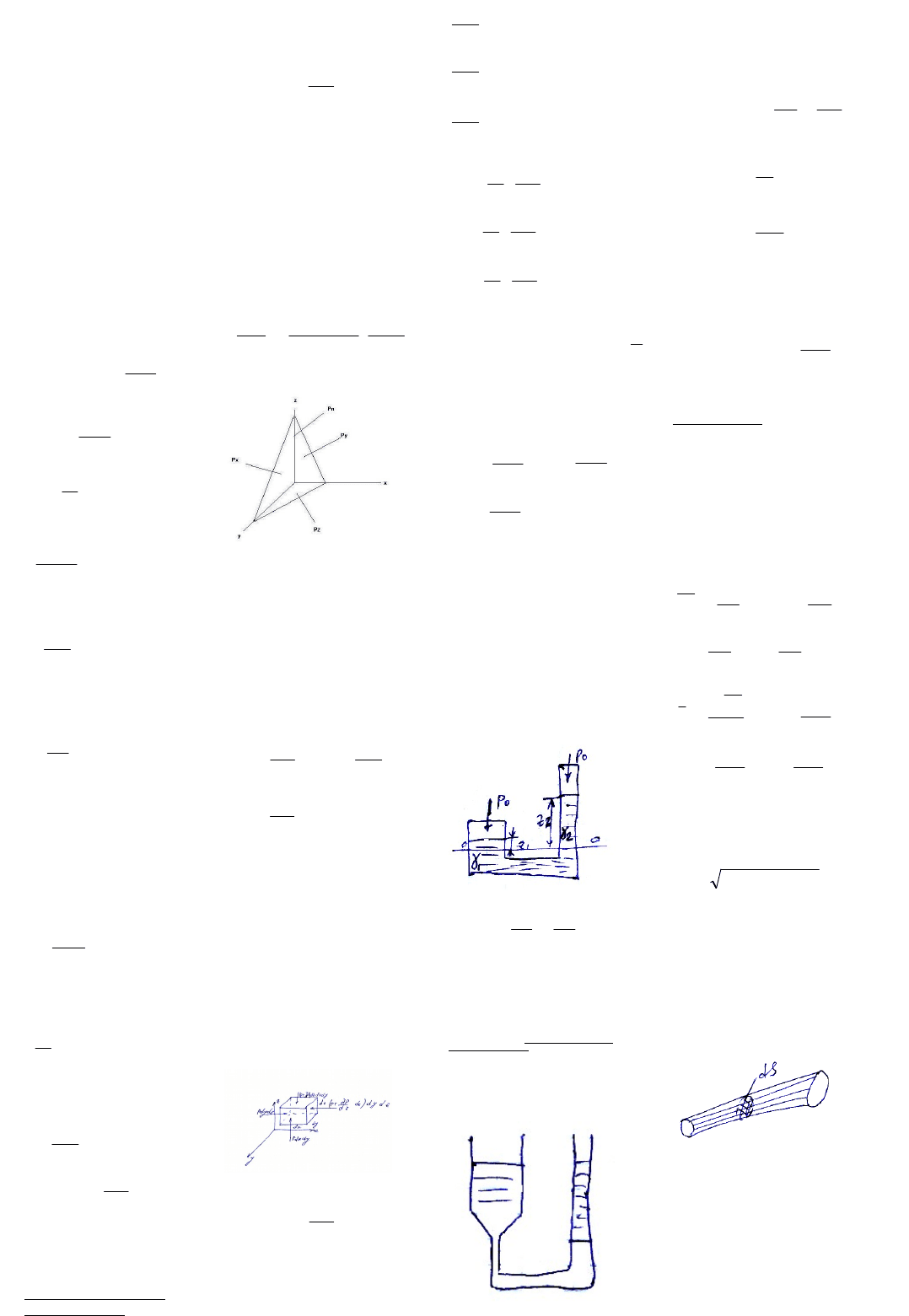
Условие равновесия элементарной жид-ти V.

Пусть S

, S

площади граней.

Поверхностные силы элементарного тетраэдра

пропорциональны произведению двух длин сторон

тетраэдра, а массовые силы пропорциональны объему,

следовательно, массовыми силами, как величинами

третьего порядка малости, можно пренебречь по

сравнению с величиной второго порядка малости.

Поверхностные силы будут направлены по

нормали грани – сила давления. Для сохранения условия

равновесия сумма всех внешних сил на координатные

оси должна быть =0.

)cos( xnPP





;

)cos( ynPP





;

)cos( znPP





Где n – орт нормали к наклонной грани

Поделим выражение на S

, S

P 

;

P 

;

P 

Из рисунка видно, что S

, S

и S

проекции

наклонной грани на соответствующую плоскость

)cos( xnSS





;

)cos( ynSS





;

)cos( znSS





Подставив эти значения получим:

, P

, т.е. P

, следовательно в

покоящейся жид-ти величина напряжения сил р

называемого гидростатическим р в точке не зависит от

ориентации площадки к которой приложено р.

Отсюда следует первый закон Паскаля.

Давление на поверхность жид-ти произведенное

внешними силами передается жид-тью одинаково во

всех направлениях.

2. Основное уравнение гидростатики условие

существования равновесия.

Рассмотрим элементарный прямоугольный

параллелепипед выделенный в покоящейся жид-ти.

Пусть грани его dx

Пусть на единицу массы действует массовая

сила Fс, имеющая составляющие вдоль оси z(x,y,z).

Тогда уравнение в проекции на ось x можно записать

















 0)( dxdydzdydx



(1)















(2)

Полученные уравнения наз-ся основным

уравнением гидростатики или уравнением Эйлера





















(3)

Умножим уравнение (3) на dx, dy, dz и сложим

dPdz

ZdzYdyXdx 











 )(



(4)

Перепишем в виде:

dPZdzYdyXdx  )(



(5)

Левая часть уравнения является тоже полным

дифференциалом.

Xdx+Ydy+Zdz=dФ













(6)

Тогда уравнение можно переписать

ρdФ=dP

Вывод: жид-ть может находиться в равновесии

только в том случае, когда проекции массовых сил

удовлетворяют условию (6).

3. Сообщающиеся сосуды.

Рассмотрим схему

+γ





U-образная трубка.

4. Закон Архимеда.

Всякое тело, погруженное в жид-ть теряет в

своём весе столько, сколько весит вытесненная телом

жид-ть.

=γ

·V

Вес вытесненной жидкости

=γ·V

– направлена в сторону, противоположную

силе тяжести и наз-ся гидростатической подъёмной

силой или силой Архимеда.

приложена в точке, которая является

центром тяжести, вытесненной телом жид-ти.

5. Капиллярные поверхностные силы.

Многие процессы в природе определяются

наличием капиллярных поверхностных сил.

Уровни в сосуде и жид-ти должны быть

одинаковы.

При опускании трубки понижение уровня

жидкости, жид-ть не вытекает, а на конце трубки

образуется мениск → в трубке действует какая-то

добавочная сила (давление), которая выравнивает силу.

… . вызывается молекулярными силами поверхностного

натяжения. Жид-ть → уменьшить свободную

поверхность, это вызвано тем, что молекулы жид-ти,

расположенные на границе жид-ти и газа почти не

притягиваются молекулами газа и силы, действующие

на них со стороны молекул расположенные со стороны

жид-ти притягивают их внутрь. Такая сила не возникает

на горизонтальных поверхностях.

Величина поверхностного натяжения на

единицу длины наз-ся коэф-том поверхностного

натяжения σ (пси).

σ не зависит от природы жид-ти от t

ры

. Условие

равновесия будет

)

(

PP 



и R

– радиусы кривизны вдоль оси x и y.

Для цилиндрических поверхностей:





Для сферических поверхностей: R





Результирующая пов. сил направлена внутрь, а

для вогнутых наружу… Форма мениска будет зависеть

от…

Если жидкость смачиваемая, то мениск

вогнутый, результ.сила –наружу.

Если не смачиваемая жид-ть (ртуть) – мениск

выпуклый, рез.сила – внутрь.

Т.е. капиллярные силы будут поднимать

столбик воды и понижать столбик ртути.

Высота будет зависеть





h 

Например: r=1мм, вода увеличивается на 10 мм.

Лекция 2

Кинематика жидкости

1. Методы Лагранжа и Эйлера.

Исследование движ-ия жид-ти.

Движ-ие тв. тела определено, если в любой

момент времени определение вектора скорости трёх его

точек, лежащих на одной прямой. Для жид-ти движения

определяют только тогда, когда в любой момент

времени изв. вектора скоростей всех частиц жид-ти.

Этим и занимается кинематика жид-ти.

Существует 2 метода исследования движ-я жид-

ти.

В методе Лагранжа изучается движение каждой

отдельной частицы.

i+y

γ+z

Движение считается определимым, если для

каждой частицы известен ее путь движения во времени

r=r(r0t)

x=x(x0,y0,z0,t)

y=y(x0,y0,z0,t) (1)

z=z(x0,y0,z0,t)

Где r, x, y, z – текущие координаты частицы

, y

, z

– переменные Лагранжа

W 

;

U 

;





;





;

Ускорение определяется как вторые

производные или производные от скорости

I 

;



;



;





В методе Эйлера изучаются изменение скорости

и других параметров происходящие во времени в точках

x, y, z.

Движение считается определимым, если

известно пространственно … в векторной или

координатной форме.

),( trWW







;

222



 UW

U=U(x, y, z, t)

υ=υ(x, y, z, t) (3)

ω=ω(x, y, z, t)



,x, y, z – переменные Эйлера

На практике многие течения жид-ти с

достаточной точностью могут быть рассчитаны с

помощью упрощенных моделей.

1) установившееся или стационарное течение

(параметры не меняются)

2) плоское или двухмерное течение (когда параметры

вдоль одной из осей координат не меняется.

3) Одномерное течение. Течение в котором

параметры жид-ти зависит от одной координаты.

Линии тока – линии пространства в каждой

точке которой в данный момент времени вектора

скорости частиц касательна.

Элементарной струйкой называется струйка

движущейся жид-ти через все точки элементарной

площадки проведены линии тока.

Полученный объемный пучок называется элементарной

струйкой, а ее боковая поверхность называется трубкой

тока.

Параметры изменяются вдоль осей струйки и не

изменяется поперек ее.

Совокупность элемент-ых струек наз-ся

потоком жид-ти..

2. Расход жидкости. Средняя скорость.

Объемным расходом жидкости Q[м

/с] наз-ся

объем жидкости, протекающий через данную

поверхность в секунду.

  



S t S

WdxdydxdzUdydzdSWdtnWQ )(cos),(





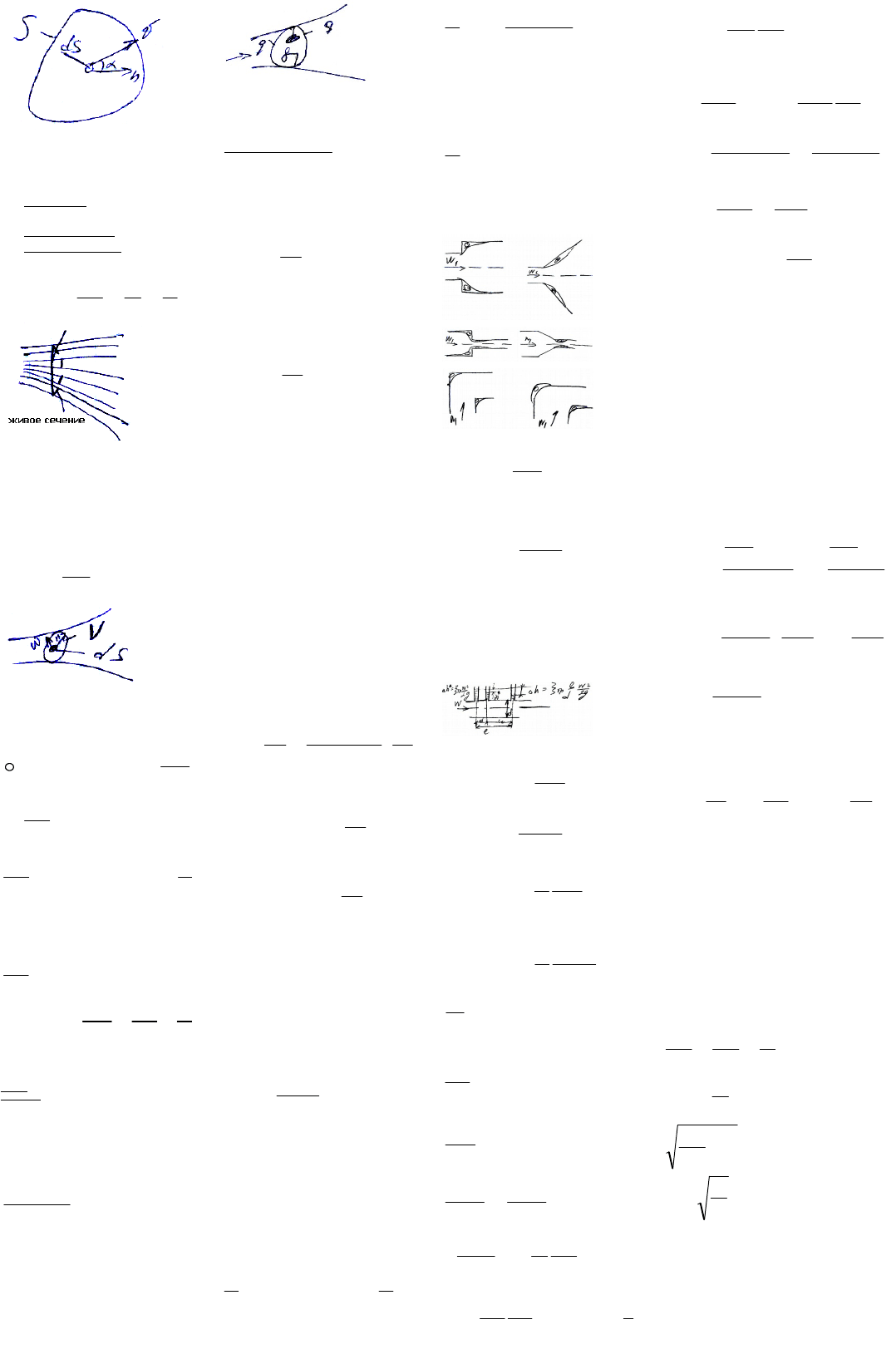
Живым сечением S

наз-ся сечение потока

каждая элементарная площадка которого нормальна

соответствующему вектору скорости.





WdSQ

Массовым расходом жид-ти G[кг/с] наз-ся

масса жид-ти, протекающая через данное сечение в

секунду.

Если ρ

по сечению одинакова то G=Qρ.

Поперечным сечением потока наз-ся сечение

площадью S перпендикулярно оси потока.

Средней расходной скоростью W

ср

наз-ся

постоянная для всего поперечного потока скорости, при

которой расход равен действительному расходу.

G=ρWcosαdS=ρW

ср



 dSW

ср





cos

В элементарной струйке скорость поперечного

сечения постоянна и если угол между линиями тока

велик, т.е. cosα=1, то расход можно записать как:

G=ρWS

ρW – плотность тока = массе жидкости, протекающей

через 1м

/с.

3. Уравнение неразрывности (уравнение

сплошности).

Называется уравнение которое выражает закон

сохранения массы и является одним из основных

уравнений гидравлики, гидродинамики.





Выделим контр. объем V, на нем элементарную

площадку dS, пусть скорость на этой площадке будет

W, а нормаль n. Разность м/у массой жид-ти

вытекающей из V и втекающей в него = изменению

массы жид-ти в нем. Изменение массы может произойти

только за счет изменения ρ при неустановившемся

течении.

 





S V

dSWn



)(

















































dydx

Wdiv

dVWdiv

)()()(

)(

0)(





div ρ d



представляет собой … вытек.

из V и втекающая в него отнесенная к единице объема и

времени. Для несжимаемой жид-ти при ρ во времени не

происходит

0)(

















dzdydx

Wdiv





Для установившегося течения расходы жид-ти,

проходящие ч/з любое поперечное сечение, одинаковы.

ср

=ρ

ср

=const

В каналах в которой жид-ть ускоряется наз-ся

сотлами или конфузорами, а в которых тормозятся –

диффузорами.

Для несжимаемой жид-ти сотлы – это

сужающиеся каналы S

, а диффузоры –

расширяющимися каналами S

Для сжимаемой жид-ти сотлами и диффузорами

могут служить как расширяющиеся, так и сжимающиеся

каналы в зависимости от усл.течения.

4. Уравн-я движения жид-ти.

Было получено Эйлером в 1755г. Получено как

обобщение второго закона Ньютона.

Wmd





)(

(1)

m – масса жид-ти



- скорость



- количество движения



- равнодействующая сила

Внутри объема могут находиться тела,

происходить обмен тепла между жид-тью и внешней

средой.

Уравнение (1) справедливо для любой частицы

находящейся в объеме, т.е.

WdVd





),,(



(2)





- равнодействующая сила, действующая

на частицу.

В общем виде уравнение движения для

контрольного объема можно записать в виде

  









V S S

dSWWdSWWdVW

2 1



- первая теорема Эйлера

Равнодействующая внеш. сил действующих в

данный момент на жид-ть в данном объеме равна

изменению во времени суммарного кол-ва движения

жид-ти в этом объеме + разность потоков движения

жид-ти на выходе и входе на контрольный объем.

5. Интегральное уравнение движения в

проекции на ось Х.

  









V S S

UdSWUdSWUdV

2 1





- проекция сил на ОХ, действующая

на твердые поверхности, соприкасающиеся с

контрольным объемом.

Для элементарной струйки:

)(

UUGR





)(

VVGR





)(

WWGR





Т.е. проекция равнодействующих внешних сил

приложенных к струйке на любом ее участке =

проекции на эту ось разности потоков кол-ва движения

на выходе и входе участков. Или равно произведению

расхода на приращение скорости. Т.о. по

установившемуся движению и известным массовым

силам, сила взаимодействия между жид-тью и

обтекаемыми ею телами расхода на приращение

скорости.

Данное уравнение широко используется в

гидравлике.

Лекция 3

Уравнение второго закона термодинамики.

Второй закон термодинамики устанавливает

направление протекания процесса в конечных

изолированных системах.

«Самопроизвольные реальные процессы

протекают необратимо, так что … сопровождаются

увеличением энтропии»



















градкг

Дж

dqdq

тр

Проинтегрируем и получим

=dq·dq

тр

=dU+PdV

lnlnln





























CSS

vpv

CSS









































lnlnln

1. Режимы течения жид-ти

Английский физик Рейнольдс в 1888г доказал

существование двух качеств. различных режимов

течения: ламинарное и турбулентное.

Ламинарное (слоистое) – течение возникает,

когда скорость потока сравнительно не велика при этом

частицы жид-ти движутся по существу не

перемешиваясь друг с другом. При увеличении скорости

течение переходит в турбулентное – струйки становятся

не устойчивыми, возникает мощный перенос тепла и

вещества между струйками, течение становится

хаотическим.

Рейнольдс на основании опытов установил, что

при различных значениях вязкости μ, плотности ρ,

скорости V, и характерного размера d переход

определяется не каким-то отдельным параметром, а

комплексом, при этом переход происходит при

определенном числе

кр

















Для круглых труб

кр

=2300

Значение Re

кр

зависит от случайных

возмущений в трубе (тряска, изменение формы и

размеров канала).

2. Гидравлические потери.

Гидравлические потери в гидросистемах, в

лопаточных машинах существенно ухудшают их

характеристики. В нефте- и газопроводах из-за потерь

каждые 100-150 м приходится устанавливать

компрессоры.

Гидросопротивление имеют и положительные

стороны (парашют, горелочные устройства).

Гидравлические потери при течении не

сжимаемой жид-ти в каналах могут быть рассчитаны с

использованием уравнения Бернулли.

Ρl

тр

-ρg(H

-H

)-ρl [Па]

 

HHl

тр



[М]

Если l=0 ρl

тр

=∆P

-P

тр









Различают 2 вида гидравлических потерь:

- местные потери

P

h

- потери на трение в прямых каналах постоянного

сечения

∆Р

тр

∆h

тр

Суммарные потери: ρl

тр

=∆P

+∆Р

тр

трМтр

hhl



Местные потери – затрата энергии жид-ти на

образование и поддержание вихрей в вязкой жидкости

вызванное изменением размеров, форм канала, а также

совершением работы трения на этом участке.

3. Виды местных потерь.

Внезапное внеплановое расширение каналов

Внезапное плановое сужение каналов

Внезапный плановый поворот канала

Местные потери считаются по формуле

Вейсбаха в долях скоростного напора.











Где W – среднемассовая скорость



- коэффициент местного

сопротивления



зависит от формы сопротивления,

числа Re, имеется в справочнике.

4. Потери на трение. Линейные потери.

Затрата энергии на преодоление трения при

течении жид-ти в каналах постоянного сечения.

Все трения зависят от числа Re, шероховатости

стенок. Потери на трение определяются по формуле

Фарси-Вейсбаха:

тртр





тр







Для трубы длиной l:

тртр







тртр











- длина трубы в калибрах

5. Течение Пуазейль – Гаген.

0const

С увеличением жидкости в трубе уменьшается

давление, а скорость остается неизменным.

0

Течение симметрично относительно оси

U 















Если проинтегрировать уравнение 2 раза, то получим:

 























222





Т.о. параболоид

max









Объемный расход будет равен объему параболоида

вращения

V параболоида вращения











max

12832

Ucp









-закон Пуазейля – Гагена

max

5,0













Коэффициент трения





закон трения для асимметричных течений при

ламинарном движении.

Из закона Пуазейля – Гагена следует потеря на

трение при ламинарном течении пропорционально

первой степени скорости, вязкости длине канала и

обратно пропорционально квадрату d трубы и не

зависит от ρ жидкости.

6. Уравнение Бернулли для потоков реальной жид-ти

в каналах.

Определим среднюю удельную кинетическую

энергию в данном сечении с учетом неравномерного

распределения скоростей.

 



S S

UdS

Умножим и разделим уравнение на U

ср







cpcp

dSU



α – коэффициент Карриалиса, коэффициент

неравномерности поля скоростей

α – отношение действительной кинетической энергии

потока к кинетической энергии с тем же расходом, но

имеющим равномерное поле скоростей. Тогда

уравнение Бернулли для реальной жидкости:

gz 





При равномерном поле скоростей α=1.

Для ламинарного движения в круглой трубе α=2.

7. Гидравлический удар.

Если при движении воды или другой жид-ти

резко изменить скорость течения (закрыть кран и т.д.),

то в трубопроводе возникает гидравлический кран,

высланный изменением давления. Гидравлический удар

– разрушение трубопровода. Жуковский изучил

московский водопровод, трубы которого разрушались,

хотя давление в водопроводе было не значительным.

Гидравлический удар можно рассматривать как

частный случай неустановившейся жид-ти. Физическую

картину гидравлического удара можно представить

следующим образом:

После закрытия резко крана не вся масса жидк-

ти прекращает движение мгновенно. Вначале

прекращает движение слой жид-ти непосредственно

соприкасающийся с задвижкой, затем последовательно

прекращает движение слой жид-ти с увеличивающим

расстояние от задвижки при этом давление увеличится

до уровня превышающего давление в напорном баке. В

каждом сечении трубопровода будет возникать

колебательный процесс, но вследствие сопротивления

колебания будут затухать. При эксплуатации …

Жуковский установил, что







 1

где



E

- модуль упругости







, а- скорость звука



a 

β – коэффициент сжимаемости жид-ти

Е зависит от температуры и давления жид-ти.

Зная Е и плотность жид-ти можно определить

повышение давления:

Wappp





- формула Жуковского.

Уменьшить ∆p можно за счет медленного

закрытия задвижки или крана, за счет использования

гидроаккумуляторов.

Лекция 4

1. Закон сопротивления гладких труб.

Закон сопротивления гладких труб впервые был

получен экспериментально

 

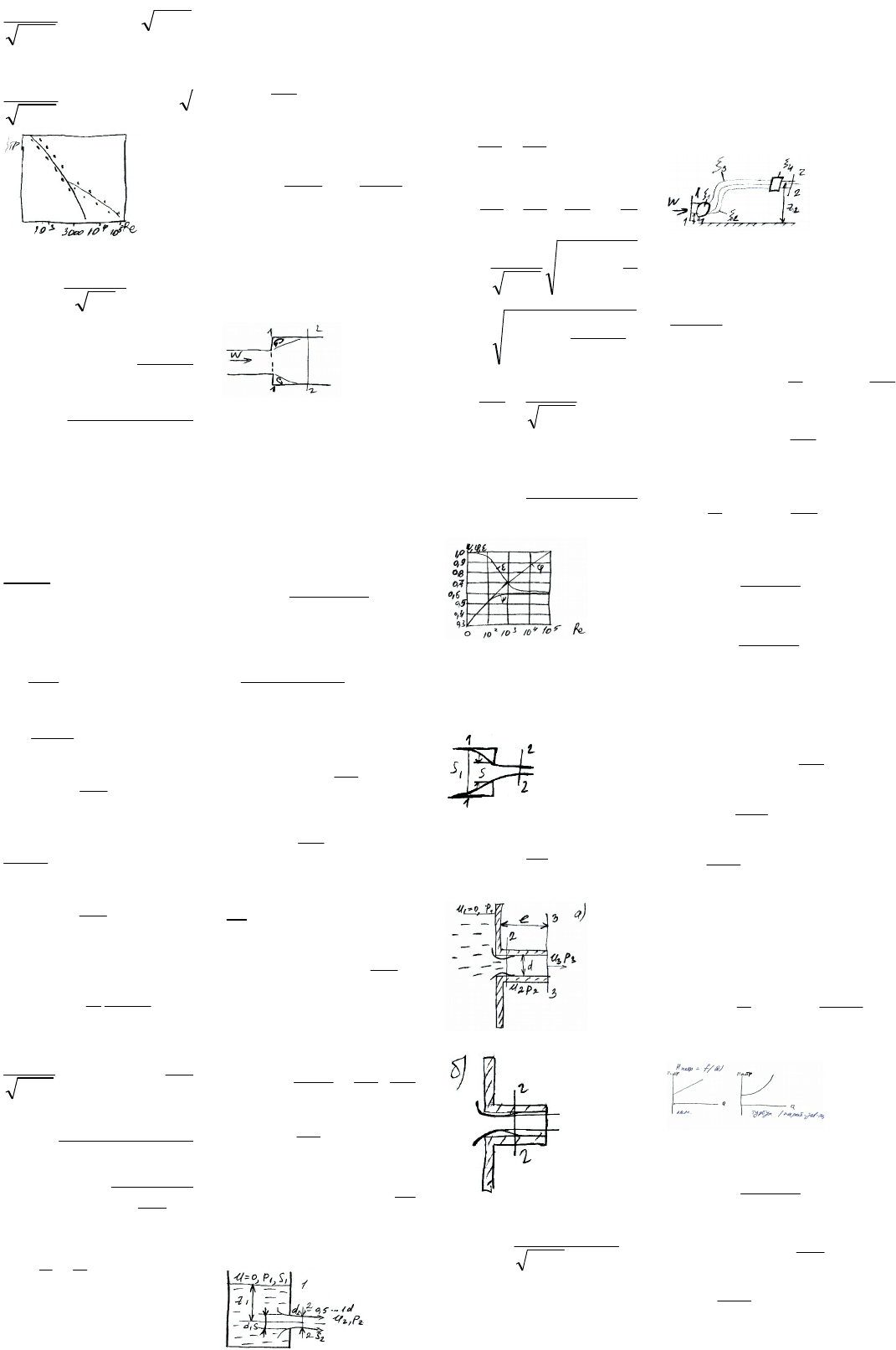
8,0Relg2

 тр

тр



- универсальный закон сопротивления для гладких труб

при турбулентном течении.

Несколько позднее получена теоретически

формула

 

9,0Relg035,2

 тр

тр



Закон сопротивления соответствующий

степенному закону распределения скоростей при n=1/7

был получен в 1811 г Блазиусом

3164,0

тр



- формула

Блазиуса

При Re< 10

В расчетах иногда используют формулу Никуладзе

237,0

221,0

0032,0 тр



Иногда используют формулу Кондакова

)5,1lg(Re8,1



тр



2. Течение шероховатого

На практике все трубы имеют ту или иную

шероховатость. Она характеризуется … степенью

гребешков. Называют абсолютной шероховатостью K

Рассматривают также относительную K

/R. При

ламинарном течении все шероховатые трубы имеют

такое же сопротивление, что и гладкие. При

турбулентном режиме рассматривают 3 случая:

1) Без проявления шероховатости, когда

сопротивление гладких и шероховатых труб совпадают,

т.е. неровности лежат в пределах ламинарного подслоя.

Такие трубы называются гидравлически гладкими.







(Re)fтр 



; υ*-

динамическая скорость

2) Переходный режим. Он наступает при увеличении

числа Re, при уменьшении величины ламинарного

подслоя.

0,1



705



















 Re

fтр



Коэффициент трения зависит от Re и от шероховатости.

3) С полным проявлением шероховатости





















fтр



. Коэффициент

трения обусловлено не трением, а завихрением, и

сопротивление не зависит от Re. Автомодельный режим

относительно Re, режим квадратической зависимости

гидравлического давления от скорости.

ср

трp







Для шероховатых труб получена интерполяционная

формула















тр



787

lg274,1

. Для рактических расчетов используется формула

Альтшуля

7Re

lg8,1

















тр



Прог. скорость шерох.труб менее напол.чем в гладких.

Они описываются степенным законом с числом n=

...

n

3. Расчет гидравлических потерь в трубах не

круглого сечения.

Rr=ПLτ

Rr – сила трения

П – смачиваемый периметр

L - длина

τ – касательные напряжения

Опыты показывают, что расчет … не круглого

сечения можно производить по тем же формулам, что и

для труб круглого сечения, если d заменить на

динамический диаметр.

Гидравлический диаметр



S – площадь поперечного сечения

Местные гидравлические сопротивления при

турбулентном течении.

Потери полного напора подсчитываются по

формуле Тарси

iм











Задача состоит в том, чтобы определить

значение … коэффициент из опытов известно, что при

турбулентном режиме



зависит от вида местного

сопротивления и практически не зависит от Re,

т.е.потери определяются вихреобразованием. Побочное



определяется по графикам, таблицам,

эмпирическим формулам. При внезапном расширении



может быть определено аналитически.

При внезапном расширении скорость

уменьшается, давление увеличивается, образуется зона

обратных токов с вихрем. Случайной называют

потерями на удар Борда-Корно:

PPP 

=α

α – коэффициент округленности

Из уравнения Бернулли мы можем получить

PPPPP

уд









Из уравнения количества движения можем получить

-P

=G(U

-U

)=U

ρS

-U

)

Уравнение расхода U

Используя записанные уравнения мы можем получить

 

































SUU





- теорема Борда-Корно

Потери полного напора равны скоростному напору

потерянной скорости

 

UU 



На практике большие потери при внезапном

расширении широко используется в логарифмических

уплотнениях.

Потери при внезапном сужении рассчитывается по

формуле Идельчика















15,0



Потери при плавном сужении канала зависит от

отношения площадей

, ξ колеблется в

диапазоне от 0,01 до 0,1.

Потери в отводах – это плавный поворот; потери

уменьшаются с увеличением радиуса поворота

отв





- в справочнике (Идельчика)

Эквивалентная длина трубопровода. При расчетах

ламинарных движений когда местное сопротивление

пропорционально скорости в первой степени потери

удобно выражать через эквивалентную длину

трубопровода – это длина такого трубопровода

заданного диаметром сопротивление которого равно

заданному местному сопротивлению.

2ReRe

экв

























Суммарные потери в этом случае

 

2Re

PPP

экв

Мтр









4. Истечение жид-ти ч/з отверстие насадки.

Этот процесс широко реализуется на практике при

подаче топлива, при подаче воды на лопасти

гидротурбин.

Пусть мы имеем ёмкость из которой через

отверстие в стенке вытекает жид-ть пот. энергия жид-ти

частично превращается в кинетическую, частично

затрачивается на приобретение местного

сопротивления. Задача состоит в том, чтобы определить

скорость U

и гидравлич. сопрот. расход. Напор пост,

т.е. z

=const, то можно считать, что U

=0.

Перепад давлений: P

+ρgz

-P

Будем считать, что отверстие мало, а стенка

тонкая. Частицы обтекая крону, движутся по

криволинейным траекториям, что называют

центробежными силами направ. к оси, которые

сжимают струю d

<d.

Отношение площадей S2/S называют

коэффициентом совершенного сжатия струи





Уравнение Бернулли

221







zgU 22



















 





Если бы ξ=0, то теор.υ>υ

действ

zgU













 





H – перепад гидравлических напоров









φ – скоростной коэффициент

Посчитаем расход в сечении 2

gHSUSUSQG

222





расходтеоретGT

расходдействитG







ψ – коэф.расхода

φψε – зависят от формы и размеров отверстий

При Re<50 велико значение коэффициента

потерь ψ. Коэффициент совершенного сжатия ε – близко

к 1. При увеличении Re за счет φ ψ возрастает, достигая

максимального значения=0,67 при Re≈350, а затем

уменьшатся за счет ε. При Re>5∙10

значение всех

коэффициентов приближ.к значению для идеальной

жид-ти.

При Re→∞; ξ→0; φ→1; ε=0,61; ψ=0,61;

Для маловязкой жидкости таких как: вода,

керосин при больших Re принимают ε=0,63; ξ=0,065;

φ=0,97; ψ=0,61;

Часто истечение из отверстия

В этом случае струя сжимается меньше, чем при

совершенном сжатии за счет направляющего действия

стенок.

=ε+0,37n

, где

n 

Истечение жид-ти ч/з внеш. цилиндрический

насадок

l=(2…6)d

По истечении через насадку возможны 2 случая:

а и б.

ε≈1,0; ψ=φ.

Потери напора определяются потерями на удар

Берда-Корно м-у сечениями 2 и 3. При Re>10

; ε=1,0;

ξ=0,5

82,01









Потери напора будут > в 7,4, чем при истечении

через отверстие тонкой стенки. U

меньшев 1,2, за счет

дополнительных потерь, расход увеличивается в 3,5 за

счет коэффициента универсального сжатия=1.

>в 1,2 т.к.P

При увеличении напора U

увеличивается, P

уменьшается и при некотором критическом значении P

равном pнасыщенных паров начинается кипение и

течение переходит в режим б.

становится=P

, а истечение становится как

истечение через отверстие тонкой стенки.

5. Гидравлический расчет трубопроводов.

Гидравлическая система в жид-ть передается ч/з

трубопровод (нефте- и газо трубопровод, системы

водоснабжения). Жид-ть может двигаться за счет того,

что пот. эн. в начале больше чем в конце. Разность пот.

эн. затрачивается на преодоление гидравлического

сопротивления и на изменение кинетической энергии.

Повыш. пот. эн. в начале трубопровода может

создаваться: 1) за счет насосов; 2) повышения давления

на свободной поверхности байки; 3) за счет разности

уровня.

Методика расчета одинакова.

Трубопроводы разделяются на простые

(постоянного сечения без разветвлений) и сложное

(различного диаметра, с разветвлениями).

Формула Бернулли, экспериментальные данные.

Лекция 5

1. Простой трубопровод

Пусть простой трубопровод расположен

произвольно в пространстве. Имеет общую длину l,

диаметр d, местное сопротивление ξ

, ξ

и t

Пусть протекает жидкость, плотность которой и

коэффициент кинем. Вязкости нам известны. Запишем

уравнение Бернулли для сечений 1 и 2. Т.к. трубопровод

имеет постоянный диаметр, то скорость можно

рассчитать U

, будем считать, что α

=α

Уравнение Бернулли:

труб

imp

































, (1)

Где

imp





















сумма гидравлических сопротивлений

ξтруб – коэффициент сопротивления всей трубы

nomp







потребляемый напор

расп







распол.напор

nomp

cQzzH 

(2)

Q-объемный расход

с и

– коэффициенты для ламинарного и турбулентного

течения

Для ламинарного течения:





;

экв







;





Подставив эти значения можно получить:

















экв

128 



(3) m=1

Для турбулентного течения:

imp























(4) m=2

Характеристикой трубопровода наз-ся зависимость

потребного напором от расхода жидкости.

Для ламинарного течения (т.к.m=1) будем иметь:

Порядок расчета для простого трубопровода зависит от

постановки задач.

1) Q, ρ, ν, размеры трубопровода, шероховатость, z

. Определить H

потр



потр





Последовательность:

1. Определить число Re:



Re

где





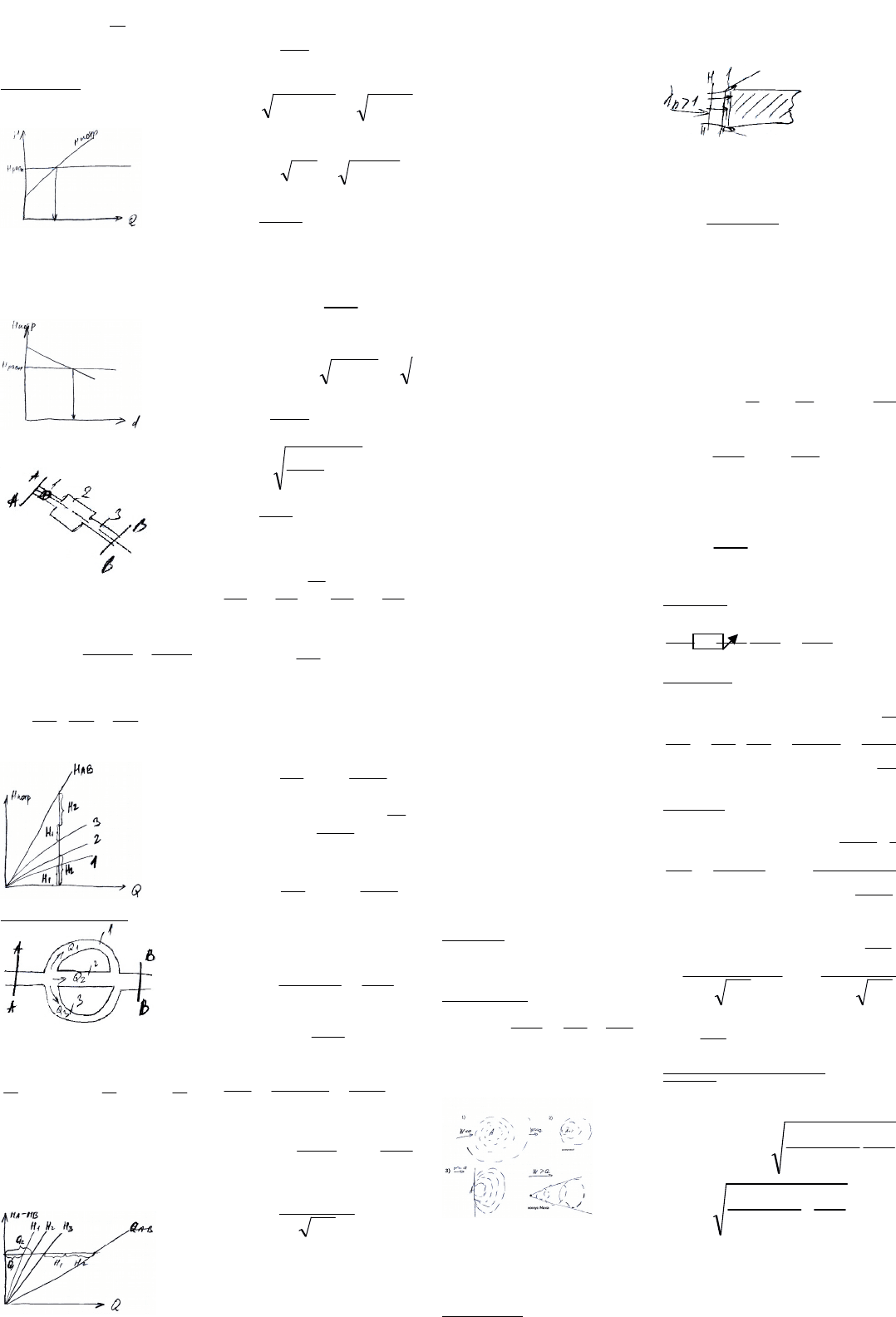
2. Определить коэффициент местных сопротивлений: ξi















fmp Re,



3. Определить Н

потр

по формулам 2, 3 или 4.

2) Даны свойства жидкости (ρ, ν), размеры

трубопровода, шероховатость, типы местных

сопротивлений, Н

расп

. Определить объемный расход (Q).

Граф. аналитический метод:

1. Задается произвольно ряд значений Q.

2. Для каждого Q определяется: Re,

коэффициенты местных сопротивлений, коэф.тр.,

потр

, как в задаче 1.

3. Строится характеристика трубопровода.

расп

мы имеем точку пересечения Н

расп

и Н

потр

даст

значение Q.

3) Задан Q, ρ, ν, типы местных сопротивлений,

размеры трубопровода кроме d, шероховатость, Н

расп

Определить d.

Граф. аналитический метод:

1. Задается ряд значений d.

2. Определяется Re для каждого значения,

коэффициент местных сопротивлений,

коэффициент потери на трение, потребный напор

как в задаче 1.

3. Строится график.

В точке пересечения d.

2. Сложный трубопровод.

1) Последовательно соединенные трубопроводы.

Пусть мы имеем 3 последовательно

соединенных трубопровода. Очевидно, что расход

проходящий через 1 трубопровод: Q

Потери напора (потери на трение) l

трА-

тр1

тр2

тр3

Выражение для потр. напора:

BmpA

AABВ

cQcQ

Нпотр 







(6)

















Построим характеристики для 1, 2 и 3 трубопровода.

Т.к. расход для всех трубопроводов

одинаковый, то Н

потр

определяется сложением.

2) Параллельно соединенные трубопроводы.

Расход которой проходит при

параллельно соединенном трубопроводе:

Q=Q

(7)

Суммарная птеря напора исходя из

уравнения Бернулли = потере напора в каждом

трубопроводе.

BAтртртрВАтр

gggg



 221)(

1111



(8)

Выразим гидравлические потери через расходы:















QcH

(9)

Значение c

и mi определяем по урав-ниям 3 и 4.

Построим характеристику параллельно

соединенных трубопроводов.

Потери напоров в каждом трубопроводе

одинаковы поэтому:

Лекция 6

1. Преобразование полной энтальпии

В энергетич. изол. сист. полная энергия

остается постоянной, т.е. энтальпия i

, T

- полная

температура.

Разница между i

и физической i:

ii 

Отсюда W в потоке:

)(

)(2)(2

***

TTR

TTiiW

ср





Макс давление будет достигнуто тогда, когда

max

∙i=T=0

***

max

22 RT

срTiW





max





Крит.W потока, Крит.υ звука, критические

параметры

Критической называется скорость равная

местной скорости звука при этом все параметры

называются W

кр

кp

кр

M 

кр

, T

кр

, ρ

кр

, P

кр

)(

)(2

kpkpkpкpкp

TTR

iikRTaW 















λ - число Маха характеризует степень преобразования

полной энергии в кинетическую (полное давление или

давление торможения заторможенного потока).

































Коэффициент сохранения полного давления

торможения:





2.Газодинамические функции.

Газодинамические функции – это безразмерные

функции λ или Маха и представляет собой отношение

параметров, комплексных параметров, размеров потока,

часто встречающихся в газодинамических параметрах.

)()1()(

1)(





























































Газодинамическая формула уравнения

неразрывности функции q(λ) и y(λ).

G=ρ

=ρWS

pkpkp

q 









)(

Заменим W на ρ





)1(

)(















)1(

)(











































Каждому значению q(λ) соответствует 2 значения λ:

λ<1, λ>1, q(λ)

max

при λ=1

)(

SqP





),( Rkfm 

3. Закон обращения воздействия.

Воздействие на поток

1) геометрическое dS≥0

2) расходное воздействие dG< >0

3) тепловое dq< >0

4) механическое dl< >0

5) гидравлические потери dl

тр

Закон обращения воздействия

 

222

1 





Из уравнения видно, что любое физическое

воздействие одинакового знака противоположным

образом влияет…

4. Распределение слабых (звуковых) волн, р, газовых

потоков.

5. Скачки укрупнения. Ударные волны.

В сверхзвуковых потоках при обтекании или

при торможении возникают скачки укрупнения или

ударные волны. У них поток тормозится ударом,

скорость снижается скачком, увеличивается ρ, p и tра.

Фронт скачка очень тонок ≈ длине своб. пробега

молекул. На скачках энтропия растет, а заторможенное

давление падает. Различают прямые, косые и

криволинейные скачки.

Прямые скачки уплотнения.

Это все скачки у которых фронт

перпендикулярен вектору скорости перед скачком.

-до скач., W

-за скач.

Прямой скачок возникает тогда, когда скорость

не меняет своего направления.

>1,

, k, R. Определить

параметры за скачком: λ

Рассм. течение расположенное очень близко от

прямой части удар. волны. S

Уравнение неразрывности: G

;

)(

1 HPHmexн

TTciiq 

Уравнение состояния: P=ρRT

dqdq





1 Н

ii 

q=0

1 Н

TT 

)(

WfW







R=0; Ф

=Ф

и Ф

можно выразить ч/з z(λ): z(λ

)=z(λ

)





111

)(











1 kpH

aWW 



Из последних двух уравнений следует, что за

прямым скачком скорость становится дозвуковой, чем

и λ

, тем <W

и λ

, и сильнее скачок.

Измерение ρ на скачке

=ρ







Измерение температуры

)(















































температура возрастает

Повышение давления

SgP

HHH







































)(





Скорость распространения ударной волны в

неподвижном газе.

Состояние уравнения неразрывности кол-ва движения

)()(











WWWSSPP













Скорость распространения ударной волны тем больше,

чем она сильнее. Ударная волна по мере продвижения

затухает.