Лекции по алгебре логики
Подождите немного. Документ загружается.


II. АЛГЕБРА ЛОГИКИ
1. Понятие алгебры
Функция типа
называется
-арной операцией на множестве ;
называется
арностью операции. Множество вместе с заданной на нем совокупностью операций
называется алгеброй, при этом используется обозначение
.
называется основным или несущим множеством алгебры . Упорядоченный набор
, где
– арность операции ,
:
n
Mϕ→
}
i
ϕ
M
n
M
1
=ϕ
n
M
{
1
, ..., , ...
m
=ϕ ϕ
∑
i
n
()
;,, ,
m
AM
ϕ……
()
1
,,,
i
nn
……
M
A
11
xx
=
1
|
x называется типом алгебры, совокупность операций −
сигнатурой.
Σ
Множество
называется замкнутым относительно операции на , если значения
на аргументах из
принадлежат . Если замкнуто относительно всех операций
алгебры , то алгебра называется подалгеброй .
MM
′
⊂
M
′
ϕ
M
ϕ
,
M
′
(
,
…
M
′
1
,,
m
ϕϕ……
A
)
) )
1
;, ,
m
AM
′′
=ϕϕ…
A
Пример 1
1. Алгебра
называется полем действительных чисел. Тип − . Все конечные
подмножества, кроме не замкнуты относительно обеих операций. Подалгеброй этой алгебры
является поле рациональных чисел.
(
;,+⋅D
{
(
2, 2
}
0,
2. Алгебра
есть алгебра подмножеств множества . Ее тип −
.
_
2;,,
A
∪∩
A
()
2, 2,1
2. Логические функции
Мы будем рассматривать множество
, в котором элементы 0 и 1 есть не числа в обычном
смысле, а несут следующую логическую интерпретацию: 0 − ложь, 1− истина.
{}
0,1
B
=
Алгебра, образованная множеством вместе со всеми возможными операциями на нем,
называется алгеброй логики.
B
Функцией алгебры логики или логической функцией от
переменных называется -арная
операция на . Итак, логическая функция
− это функция, принимающая значения 0 или
1, аргументы которой тоже принимают значения 0 или 1. Множество всех логических функций
обозначается
, множество всех логических функций переменных − . Всякая логическая
функция
переменных может быть задана таблицей, в левой части которой перечислены все
упорядоченных наборов значений переменных из
элементов 0 или 1. В правой части таблицы
располагаются значения функции на этих наборах. Такие таблицы называются таблицами
истинности.
n n
B
P
1
(, , )
n
fx x…
n
2
n
2
()
Pn
n
2
n
Наборы значений переменных, на которых функция принимает значение 1, называют
единичными наборами функ-
ции . Наборы, на которых принимает значение 0, называют нулевыми наборами функции .
Ниже дан пример табличного задания логической функции трех переменных.
f
f f f
123
xx x
f
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
0
1
0
0
1
1
0
0
Логическая функция
переменных полностью определяется вектор-столбцом своих значений,
размерность которого равна числу наборов значений функции, т. е.
. Отсюда число различных
n
2
n
15
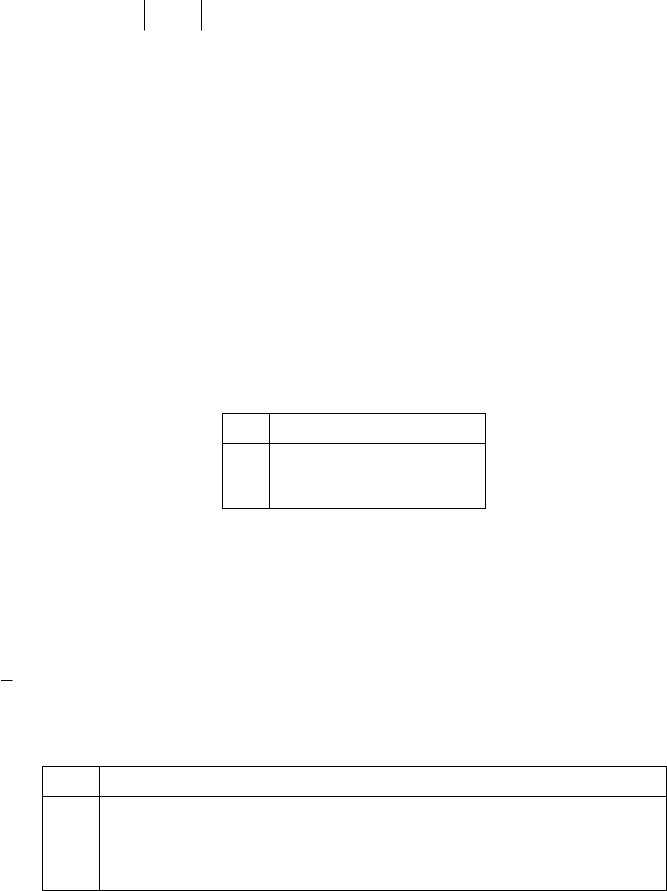
функций переменных
n
()
2
Pn
fx
11
,,
x
1
(, ,
n
x…
11
, ,
ii
x
−+
…
g
равно числу различных двоичных наборов длины
и,
следовательно, равно
.
2
n
2
2
n
(,
3
ϕ
x
x
′
2
x
ψ
&
x
∨
2
x
∼
1
x
1
x
⋅
1
x
Переменная
в функции называется фиктивной, если при любых
значениях остальных переменных выполняется равенство
i
x
111
(, , ,, , , )
iii n
x xx x
−+
……
1 111
( ,0, ,, ) (,, ,1, ,,)
ii n ii
fx x x fx x x x
−+ −+
=…………
n
)
.
В этом случае функция
, по существу, зависит от
переменной, т. е. представляет
собой функцию
. Говорят, что получена из удалением фиктивной
переменной, а получается из введением фиктивной переменной. Переменные функции ,
которые не являются фиктивными, называются существенными.
)
fx
1
,
x
(
1
n
−
, )
n
gx x
…
g f
f f
2.1. Логические функции одной и двух переменных
Число логических функций одной переменной равно 4. Все эти функции приведены в следующей
таблице:
x
0
ϕ
ϕ
1
ϕ
2
ϕ
3
0
1
0
1 1
0
0 1 0 1
Функции
и − константы 0 и 1 соответственно. Их значения не зависят от значения
переменной
. Значения функ-
ции
совпадают со значениями переменной . Поэтому функция называется тождественной
функцией и обозначается
. Значения функции противоположны значениям переменной и
поэтому она называется отрицанием
или функцией не. Для функции используются
обозначения:
0
ϕ
x
1
ϕ
x
1
ϕ
2
ϕ
x
2
ϕ
x
,
¬
, .
x
Рассмотрим логические функции двух переменных. Всего существует 16 различных логических
функций двух переменных. Все эти функции даны в следующей таблице:
1
x
0
ψ
ψ
ψ
ψ
1 2
ψ
3
ψ
4
ψ
5 6
ψ
7
ψ
8
ψ
9 10
ψ
11
ψ
12 13
ψ
14
ψ
15
ψ
0 0
0 1
1 0
1 1
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
В данной таблице функции
и есть константы 0 и 1 соответственно, т.е. имеют по две
фиктивные переменные.
0
ψ
15
ψ
Функция
называется конъюнкцией и . Для функции используют обозначения: ,
, . Иногда знак операции опускают и пишут . Функция равна 1, только если и
равны 1. Поэтому конъюнкцию часто называют функцией и. Еще одно название − «логическое
умножение», так как ее таблица совпадает с таблицей обычного умножения для чисел 0 и 1.
1
ψ
2
x
1
x
2
x
1
ψ
12
xx
112
xx
∧
2
x
12
xx
1
ψ
Функция
называется дизъюнкцией и . Для нее используются обозначения: ,
. Функция равна 1, если или равны 1. Поэтому ее часто называют функцией или.
7
ψ
ψ
1
x
2
x
12
xx
1
xx+
2
2
2
2
7
ψ
1
x
2
x
Функция
называется сложением по модулю 2. Ее обозначения: , , . Она
равна 1, когда значения ее аргументов различны, и равна 0, когда они равны. Иногда
называют
неравнозначностью.
6 12
xx
⊕
12
xx
1
x
≠
6
ψ
Функция
называется эквивалентностью или равнозначностью. Ее обозначения: ,
. Она равна 1, когда значения ее аргументов совпадают, и равна 0, когда они различны.
9
ψ
13
ψ
12
xx
1
xx≡
Функция
называется импликацией и . Ее обозначения: , и часто
читается «
имплицирует » или «из следует ».
1
x
2
x
2
12
xx→
1
xx⊃
2
x
1
x x
8
ψ
Функция
называется стрелкой Пирса. Она обозначается
и часто читается «ни
, ни
». Ее значения на соответствующих наборах противоположны значениям дизъюнкции, поэтому ее
еще называют антидизъюнкцией или «не − или».
1
xx
↓
2
x
16

Функция называется штрих Шеффера. Она обозначается и часто читается «не или
не
» или «
x
и не совместны». Значения функции на соответствующих наборах
противоположны значениям конъюнкции, поэтому ее еще называют антиконъюнкцией или «не − и».
14
ψ
1
12
|
xx
12
|
x
1
x
2
x
2
x x
В функциях
ψ
и переменная фиктивная: и
3 12
ψ
2
x
()
312
,
xx x
ψ=
1
()
12 1 2 1
,
xx x
ψ=
()
.
()
В функциях
ψ
и фиктивна переменная : ψ= и
5 10
ψ
1
x
512 2
,
xx x
10 1 2 2
,
xx x
ψ=.
Таким образом, из 16 логических функций двух переменных шесть функций имеют фиктивные
переменные. С ростом
доля функций, имеющих фиктивные переменные, убывает и стремится к
нулю.
n
2.2. Суперпозиции и формулы
Пусть даны функции
и
. Говорят, что функция
получена
подстановкой в , если имеет место равенство
, где
.
:
fA B
→ :
gB C
→
m
:
hA C→
f g
()
(
()
hx g f x
=
)
A
→
)
)
f
}
)
)
3
2
xA∈
Пусть задано множество функций типа:
. Тогда возможны любые
подстановки этих функций друг в друга, а также любые переименования аргументов. Например,
переименование
в порождает из функции четырех аргументов функцию трех
аргументов
. Функция, полученная из
некоторой подстановкой
их друг в друга и переименованием аргументов, называется суперпозицией
. Выражение,
описывающее эту суперпозицию и содержащее функциональные знаки и символы аргументов,
называется формулой. Формулы, как правило, состоят из других формул (подформул) и поэтому
имеют древовидную структуру. При этом важно такое понятие, как глубина формулы.
1
:
f
1
,, :
n
m
n
AAfA
→…
fx
1
,,
n
f…
3
x
12
,,
x
2
x
()
4
≡
(
1234
,,,
x xx
f
1
,,
f…
(
1234
,,,
g xx fxxxx
n
Пусть дано множество логических функций
. Символы переменных
есть формулы глубины 0.
{
1
,, ,
m
ff
Σ= ……
1
,,,
n
xx……
Формула имеет глубину
, если она имеет вид
, где
,
− число
аргументов
, а подформулы, максимальная из глубин которых равна . Функция
называется внешней или главной операцией формулы .
F
i
f
1
k +
()
1
,,
i
in
fF F
…
i
f ∈Σ
k
i
n
1
,,
i
n
FF…
i
f
F
Пример 1
1.
− формула глубины 1.
(
12
,
fxx
2.
− формула глубины 2, содержащая подформулу глубины 1. Если, например,
− дизъюнкция, − конъюнкция, то данная формула имеет вид
()
.
()
(
2112 3
,,
ffxx x
2
f
1
f
12
&
xx x
∨
Всякая формула, выражающая функцию как суперпозицию других функций, задает способ ее
вычисления. Этот способ определяется следующим очевидным правилом: формулу можно вычислить,
только если можно вычислить все ее подформулы.
f
Для заданного набора значений аргументов можно вычислить значения всех подформул и получить
значение функции. Таким образом, формула каждому набору значений аргументов ставит в
соответствие значение функции и, следовательно, может наряду с таблицей служить способом задания
и вычисления функции. В частности, по формуле, вычисляя ее на всех
наборах, можно
восстановить таблицу функции. О формуле, задающей функцию, говорят, что она реализует или
представляет эту функцию. В отличие от табличного представление данной функции формулой не
единственно. Например, функцию
можно представить формулами
2
n
1
xx⊕
()()
12 12
&
xx xx
∨∨,
()(
12 12
&&
xx xx
∨
12
xx⊕=
)
. Формулы, представляющие одну и ту же функцию, называются
эквивалентными или равносильными. Эквивалентность формул обозначается знаком равенства.
Например,
()(
12
xx
∨
)
)
12
&
xx
=∨ . Эквивалентность формул можно установить путем
построения таблиц по каждой формуле и последующего их сравнения.
2.3. Двойственность логических функций
Функция
называется двойственной к , если
(
11 2
,,
fx x
…
()
21 2
,,
fx x
…
()()
11 2 21
,, ,,
n
fx x f x x
=…….
Беря отрицание над обеими частями равенства и подставляя
1
,,
n
x… x
вместо , получим
1
,,
xx…
2
()
()
()
11 2 21 21 2
,, ,, ,,
n
fx x f x x f x x
==………,
17

т. е. функция является двойственной к . Таким образом, отношение
двойственности логических функций является симметричным. Двойственная функция к
обозначается . Если функция совпадает с функцией, которая является
двойственной к ней, то такая функция называется самодвойственной.
(
21 2
,,
fx x
…
(
*
12
,,
fx x
…
)
)
)
2
(
11 2
,,
fx x
…
)
2
()
12
,,
fx x
…
(
1
,,
fx x
…
Пример 1
1. Двойственные функции:
10,
,
()
,
.
*
=
()
*
12 1
&
xx x x
∨=
2
*
12 1
xx xx
⊕=∼
2
()
*
12 1
|
xx x x
=↓
2. Самодвойственные функции:
, x x , .
12 13 23
xx xx x x∨∨
Справедлив следующий принцип двойственности. Если в формуле , представляющей функцию
, все знаки функций заменить на двойственные им, то полученная формула
будет представлять
функцию
, двойственную к .
F
f
*
F
*
f
f
Пример 2
Пусть логическая функция задается формулой
. Используя принцип
двойственности, построим формулу, реализующую двойственную функцию к данной. Так как
,
()
,
()(
fxy zt
=∨→⊕
)
y
()
*
&
xy x y
∨=
*
xy x
⊕=∼
()
*
xy x
→=⋅
y
, то получаем
*
(&)(
f xyx
=⋅
) (|)( )
y xyxy
=⋅
∼∼.
3. Булева алгебра логических функций
и эквивалентные преобразования в ней
3.1. Разложение функций по переменным
Обозначим
следующую функцию
t
x xt x t
⋅∨ ⋅ . Тогда легко проверить, что выполняются равенства
, 0,
, 1,
t
xt
x
xt
=
=
=
1, ,
0, .
t
xt
x
xt
=
=
≠
Теорема 1
Всякая логическая функция
может быть представлена в следующем виде:
1
(, , )
n
fx x…
1
1
11 11
1
( ,..., )
( ,..., , ,..., ) ... ( ,..., , , , ),
m
m
t
t
mm n m mm n
tt
fx x x x x x ft t x x
++
=∨
…
(3.1)
где дизъюнкция берется по всем
наборам значений переменных
tt
.
2
m
1
,...,
m
Доказательство
Равенство (3.1) проверяется подстановкой в обе части произвольного набора .
Поскольку 1
, только когда
, то среди
наборов
только та конъюнкция
равна 1, для которой
. Все остальные конъюнкции
равны 0.
()
11
,,, ,,
mm n
ttt t
+
……
1
1
...
m
t
t
m
xx
t
x
=
xt
=
m
x t
2
m
(
1
,...,
m
tt
1
1
t
x
)
m
=
11
,,
xt=…
...
m
t
m
x
Представление логической функции (3.1) называется разложением по переменным
1
,..., .
m
xx
При
получаем разложение функции по одной переменной
1
m =
fx
11212
( ,..., ) (0, ,..., ) (1, ,..., )
nn
xxfxxxfxx=∨
. (3.2)
n
n
При
m
=
n
разложение имеет вид
1
1n
1
1
( ,...,t )=1
( ,..., ) ...
n
t
t
n
ft
fx x x x
=∨ , (3.3)
где дизъюнкция берется по всем единичным наборам функ-
ции .
f
Существует другое разложение по переменным, в котором в отличие от (3.1) дизъюнкции меняются
на конъюнкции, а конъюнкции − на дизъюнкции.
Теорема 2
Всякая логическая функция
может быть представлена в следующем виде:
1
(, , )
n
fx x
…
18
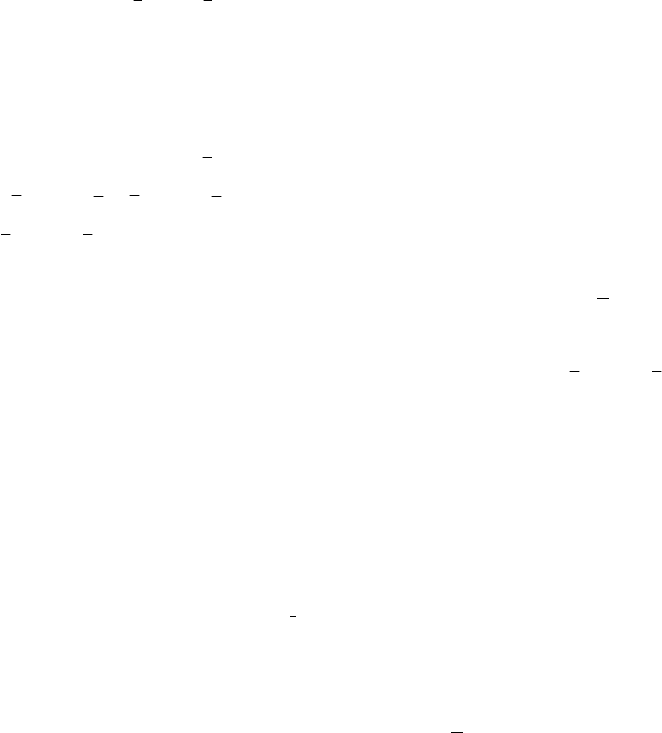
1
1
11 11
1
( ,..., )
( ,..., , ,..., ) & ( ... ( ,..., , , , )),
m
m
t
t
mm n m mm n
tt
fx x x x x x ft t x x
++
=∨∨∨
…
m
(3.4)
где конъюнкция берется по всем
наборам значений переменных
t
.
2
1
,...,
m
t
Доказательство
Равенство (3.4) проверяется подстановкой в обе части равенства (3.4) произвольного набора
. Поскольку
()
11
,, , ,,
mm n
ttt t
+
……
0
t
x
= , только когда
, то среди
наборов
(
только та
дизъюнкция
xt
=
2
m
)
1
,...,
m
tt
1
1
...
t
∨∨
m
t
m
xx
1
1
...
m
t
t
m
x
∨∨
x
равна 0, для которой
. Все остальные
дизъюнкции
11
xt
,,
mm
x=… t=
1
1
...
t
x
∨∨
1
m =
m
t
m
x
равны 1.
При
получаем разложение функции по одной переменной
112 12
( ,..., ) ( (0, ,..., )) & ( (1, ,..., ))
nn
fx x x f x x x f x x
=∨ ∨
n
. (3.5)
При
m
=
n
разложение имеет вид
1
1n
1
1
( ,...,t )=0
( ,..., ) & ( ... )
n
t
t
nn
ft
fx x x x
=∨∨. (3.6)
В равенствах (3.3) и (3.6) произвольная логическая функция представлена в виде формулы,
содержащей знаки функций дизъюнкции, конъюнкции и отрицания.
3.2. Булева алгебра функций
Формулы, содержащие кроме переменных только знаки функций дизъюнкции, конъюнкции и
отрицания называются булевыми формулами.
Теорема 3
Всякая логическая функция может быть представлена булевой формулой, т. е. как суперпозиция
конъюнкции, дизъюнкции и от-рицания.
Доказательство
Для всякой функции, кроме константы 0, таким представлением может служить ее разложение по
все переменным. Константу 0 можно представить формулой
xx
.
Пусть функция
задана формулой , а функция формулой . Подстановка и в
дизъюнкцию
дает формулу
. Если взять
и , то будет
эквивалентна формуле . При этом обе эти формулы представляют одну и ту же логическую
функцию, которую мы обозначим
Таким образом, дизъюнкцию можно рассматривать как
бинарную операцию на множестве логических функций, которая каждой паре логических функций
и
независимо от формул, которыми они представлены, однозначно ставит в соответствие функцию
1
f
2
1
F
1
F
∨
2
.
f
2
f
2
F
′
1
F
1
′
∨
2
F
′
1
xx∨
2
F
1
f∨
1
FF
′
=
1 2 2
2
);
1
3
)
2
FF
=
FF
1
FF
∨
1
f
2
f
ff
∨
12
.
Аналогично можно рассматривать конъюнкцию и отрицание как операции над логическими
функциями.
Если рассматривать множество логических функций
Р
2
и три операции
, то алгебра
называется булевой алгеброй логических функций.
_
2
(;,&,)
P
∨
_
2
(;,&,)
P
∨
Операции булевой алгебры
называют булевыми операциями.
_
2
(;,&,)
P
∨
3.3. Основные свойства булевых операций
1. Ассоциативность
:
123 123
()()
xxx xx x=
,
12 31 23
() (
xx xx x x∨∨=∨∨
2. Коммутативность
:
12 21
xx x x=
, ;
122
xx x x∨=∨
3. Дистрибутивность
:
12 3 121
()
xx x xx xx⋅∨=⋅∨⋅
, ;
123 1213
()( )(
xxx xxxx∨⋅=∨⋅∨
4. Идемнотентность
:
19

xx x⋅=, ; xxx∨=
5. Двойное отрицание
:
xx
= ;
6. Свойства констант
:
&1
x=
11
x ∨=
x
, ;
&0 0
x =
0
xx∨=
, ;
01
= ,
1
;
0
=
7. Законы де Моргана
:
1
12
&
xxxx
=∨
2
,
12
12
&
xx x x
∨= ;
8. Закон противоречия
:
&0
xx= ;
9. Закон «исключенного третьего»
:
1.
xx∨=
Все эти равенства остаются справедливыми при подстановке вместо переменных любых
логических функций и, следовательно, любых формул, представляющих эти функции. При этом
необходимо соблюдать следующее правило подстановки формулы вместо переменной: при
подстановке формулы
F
вместо переменной
все вхождения переменной в исходной равенство
должны быть одновременно заменены формулой
F
.
x x
Это правило подстановки позволяет получить из приведенных соотношений новые эквивалентные
соотношения.
Если какая-либо формула
F
содержит
F
1
в качестве подформулы, то замена
F
1
на эквивалентную
формулу даст эквивалентную
F
.
F
′
В этом заключается правило замены подформул, которое позволяет, используя эквивалентные
соотношения, получать формулы, эквивалентные данной.
Преобразования формул, использующие эквивалентные соотношения и правило замены,
называются эквивалентными преобразованиями.
Эквивалентные преобразования являются мощным средством доказательства эквивалентности
формул.
Рассмотрим некоторые основные эквивалентные преобразования в булевой алгебре. Отметим, что в
булевой алгебре принято опускать скобки в следующих двух случаях:
а) при последовательном выполнении нескольких конъюнкций или дизъюнкций, например,
или ;
123 123
()
xxx xxx
=
12312
()
xxxxxx
∨∨=∨∨
3
x
б) если они являются внешними скобками у конъюнкции: например, вместо
.
12 3 45 12 3 45
(( ))( ) пишут ()
xx x xx xx x xx
∨∨ ∨∨
Оба соглашения совершенно аналогичны общепринятому опусканию скобок для умножения в
арифметических формулах.
Рассмотрим некоторые эквивалентности, позволяющие делать упрощения в формулах в процессе
эквивалентных преобразований:
а)
Поглощение
:
;
.
xxyx
∨= ( )
xx y x
∨=
Доказательство первого равенства:
. Второе равенство
сводится к первому, если применить дистрибутивный закон в левой части.
&1
xxyx xy
∨= ∨=
()
1&1
xyx
=∨= =
б)
Склеивание
:
.
xy x y x
∨=
Доказательство:
()
&1
xy x y x y y x x∨= ∨= =.
в)
Обобщенное склеивание
:
xz yz xy xz y z
∨∨=∨.
Доказательство:
(1 ) (1 )
xz yz xy xz y z xyz xyz xz y yz x xz yz
∨∨=∨∨ ∨ = ∨∨ ∨=∨
.
г)
xxyxy
∨=∨.
Доказательство:
( )&( ) 1&( )
xxy xx xy xy xy
∨=∨ ∨= ∨=∨
) (0, ,... )
x x fxx∨=∨⋅
.
д)
.
112 1 2
( , ,...
nn
xfxx
Равенство д) проверяется подстановкой двух возможных значений переменной
: 0 или 1.
1
x
4. Нормальные формы
Разложение логической функции
по всем переменным в виде
1
( ,..., )
n
fx x
1
1n
1
1
( ,...,t )=1
( ,..., ) ...
n
t
t
n
ft
fx x x x
=∨
n
, (4.1)
20

называется совершенной дизъюнктивной нормальной формой (СДНФ).
Из того, что для любой логической функции существует разложение по переменным, следует, что
любая логическая функция, кроме 0, может быть представлена в виде СДНФ. Из построения СДНФ,
видно, что такое представление однозначно.
Для построения СДНФ можно использовать таблицу функции. Так как в представлении (4.1)
участвуют только единичные наборы, и
, только когда
, и
t
x
=
x
1
t =
t
x
=
x
)
, только когда
, то для
каждого единичного набора составляется конъюнкция переменных по следующему правилу:
переменная входит в конъюнкцию без отрицания, если в наборе она равна 1, и с отрицанием, если в
наборе ее значение равно 0. СДНФ есть дизъюнкция построенных таким образом конъюнкций.
0
t =
Пример 1
Пусть дана таблица функции трех переменных.
Требуется построить СДНФ этой функции. У этой функции четыре
единичных набора:
, , ,
(
. Для каждого из этих наборов
составим соответственно по изложенному выше правилу конъюнкции
переменных:
()
000
()
011
()
101 111
12
xx
3
x
,
123
xx x
,
12
xx x
3
xx
, . Взяв дизъюнкцию этих
конъюнкций, получим СДНФ
1
x
2
x
3
x
f
0 0 0 1
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 0
1 1 1 1
123
x
123 123 123 123
xxxxxxxxxxx
=∨∨∨
СДНФ
fx
.
Разложение логической функции
по всем переменным в виде
1
( ,..., )
n
fx x
1
1n
1
1
( ,...,t )=0
( ,..., ) & ( ... )
n
t
t
nn
ft
fx x x x
=∨∨ (4.2)
называется совершенной конъюнктивной нормальной формой (СКНФ).
Аналогично, как для СДНФ, справедливо утверждение о том, что любая логическая функция, кроме
1, может быть однозначно представлена в виде СКНФ.
Также для построения СКНФ можно использовать таблицу функции. Так как в представлении (4.2)
участвуют только нулевые наборы, и
t
x
=
x
, только когда
, и
0
t =
t
x
=
x
)
, только когда
, то для
каждого нулевого набора составляется дизъюнкция переменных по следующему правилу: переменная
входит в дизъюнкцию без отрицания, если в наборе она равна 0, и с отрицанием, если в наборе ее
значение равно 1. СКНФ есть конъюнкция построенных таким образом дизъюнкций.
1
t =
Пример 2
Для функции, заданной в Примере 1, требуется построить СКНФ. Нулевые наборы:
, ,
, . Составим дизъюнкции переменных:
()
001
()
010
()
100
(
110
12
xx x∨∨
3
,
12
xx x∨∨
3
,
12
xx∨∨
3
x
,
12
x∨
3
xx∨
.
Конъюнкция этих дизъюнкций есть СКНФ данной функции:
СКНФ 123 123 123 123
()&()&()&(f xxx xxx xxx xxx
=∨∨ ∨∨ ∨∨ ∨∨
).
Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которых
каждая переменная встречается не более одного раза. Число переменных, входящих в элементарную
конъюнкцию, называется рангом элементарной конъюнкции. По определению константа 1 считается
элементарной конъюнкцией ранга 0.
Примеры элементарных конъюнкций:
,
1
x
3
x
,
34
xx
,
123
xx x
.
Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкции
элементарных конъюнкций.
Примеры ДНФ:
12 123
xx xx x
∨
,
212
xxxx
∨
4
.
Конъюнкции, входящие в ДНФ, называются слагаемыми. Число слагаемых в ДНФ называется
длиной ДНФ.
Основные отличия СДНФ от ДНФ:
а) если в СДНФ в каждой конъюнкции присутствуют все переменные функции с отрицанием или
без отрицания, то в конъюнкциях, входящих в ДНФ, могут отсутствовать некоторые переменные;
б) для каждой логической функции существует только одна СДНФ, в то время как ДНФ может быть
не единственной для одной и той же логической функции.
Пример 3
Следующие две ДНФ эквивалентны:
212321
xxxxxxx∨=∨
3
. Им соответствует СДНФ
123 123 123 123 123
xx x xx x xx x xx x xx x∨∨∨∨
.
Приведение логической функции к СДНФ можно осуществить двумя способами:
21
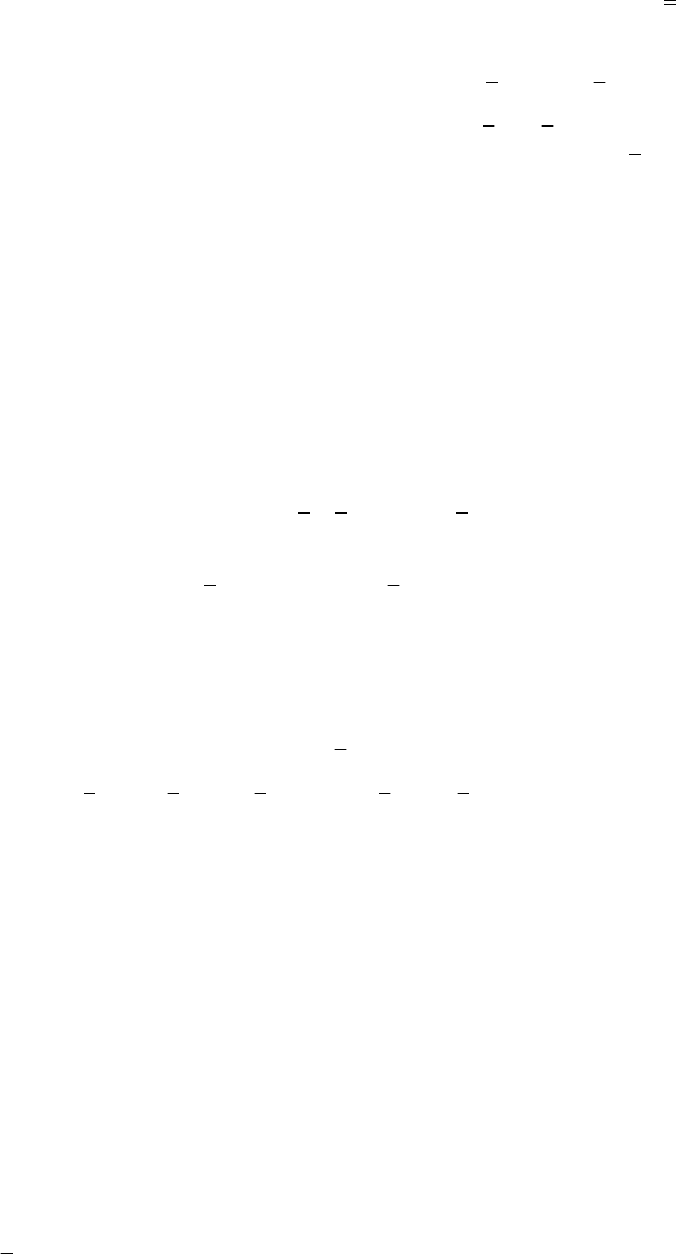
1) с помощью таблиц истинности;
2) с помощью эквивалентных преобразований; сначала строят ДНФ, а затем СДНФ.
При использовании эквивалентных преобразований для приведения к ДНФ выполняется следующая
последовательность действий:
1) с помощью эквивалентных преобразований все подформулы выражаются в виде суперпозиции
дизъюнкции, конъюнкции, отрицания;
2) все отрицания «спускают до переменных» с помощью двойного отрицания
xx
= и законов де
Моргана;
3) раскрывают скобки с использованием закона дистрибутивности:
;
()
xyz xyxz
⋅∨=∨
1
xx∨=
4) с помощью эквивалентностей
, , xx x⋅= xxx∨=
0
xx = , удаляются лишние
конъюнкции и повторения переменных в конъюнкциях;
5) с помощью эквивалентностей
, , ,
00
x ⋅=
11
x ∨=
0
xx∨= 01= , 10= удаляются константы.
Для перехода от ДНФ к СДНФ используется правило «расщепления»:
Kx Kx K∨=.
Если из формулы
с помощью некоторых эквивалентных соотношений можно получить формулу
, то можно получить из , использую те же эквивалентные соотношения. То есть всякое
эквивалентное преобразование обратимо. Используя это замечание, можно доказать следующую
теорему.
1
F
2
F
1
F
2
F
Теорема 4
Для любых двух эквивалентных формул
и существует эквивалентное преобразование в
.
1
F
2
F
1
F
2
F
Доказательство
Преобразуем
и в СДНФ. Поскольку и эквивалентны, то их СДНФ совпадают.
Обратив преобразование от СДНФ к
, получим эквивалентное преобразование от к :
.
1
F
2
F
1
F
2
F
2
F
1
F
2
F
12
F СДНФ F⇒⇒
Элементарной дизъюнкцией называется дизъюнкция переменных или их отрицаний, в которых
каждая переменная встречается не более одного раза.
Примеры элементарных дизъюнкций:
,
1
x
3
x
,
34
xx∨
,
12
xx x∨∨
3
.
Конъюктивной нормальной формой (КНФ) называется формула, имеющая вид конъюнкции
элементарных дизъюнкций.
Примеры КНФ:
12 123
()&(
xx xx x∨∨∨
)
,
2124
&( )
xxxx∨∨ .
Основные отличия СКНФ от КНФ:
а) если в СКНФ в каждой дизъюнкции присутствуют все переменные функции с отрицанием или
без отрицания, то в дизъюнкциях, входящих в КНФ, могут отсутствовать некоторые переменные;
б) для каждой логической функции существует только одна СКНФ, в то время как КНФ может быть
не единственной для одной и той же логической функции.
Пример 4
Следующие две КНФ эквивалентны:
()
21 2 3
xxxx
⋅∨∨ =
(
213
xxx
=⋅ ∨ . Им соответствует СКНФ
)
()()()()(
123 123 123 123 123
xx x xx x xx x xx x xx x
∨∨ ⋅ ∨∨ ⋅ ∨∨ ⋅ ∨∨ ⋅ ∨∨
)
)
.
Для одной логической функции
переход от КНФ к ДНФ можно осуществить с помощью эквивалентных преобразований. Для этого
выполняется следующая последовательность действий:
1) с помощью дистрибутивного закона переходят к конъюнкциям:
;
()
xyz xyxz
⋅∨=∨
2) удаляются лишние конъюнкции и повторения переменных в конъюнкциях с помощью
эквивалентностей:
,
,
;
AABA
∨=
AAA
∨=
AA A
⋅=
3) удаляются лишние константы с помощью эквивалентностей:
,
.
1
AA
⋅=
0
AA∨=
Приведение логической функции к СКНФ можно осуществить двумя способами:
1) с помощью таблиц истинности;
2) с помощью эквивалентных преобразований; сначала строят КНФ, а затем СКНФ.
При использовании эквивалентных преобразований для приведения к КНФ выполняется
следующая последовательность действий:
1) с помощью эквивалентных преобразований все подформулы выражаются в виде суперпозиции
дизъюнкции, конъюнкции, отрицания;
2) все отрицания с помощью двойного отрицания и законов де Моргана «спускаются до
переменных»;
3) с помощью закона дистрибутивности
переходят к конъюнкции
дизъюнкций;
()(
xyz xy xz
∨=∨⋅∨
4) удаляются лишние дизъюнкции и переменные в них с помощью эквивалентностей:
,
,
AA A
⋅=
xxx∨=
1
xx∨=;
22
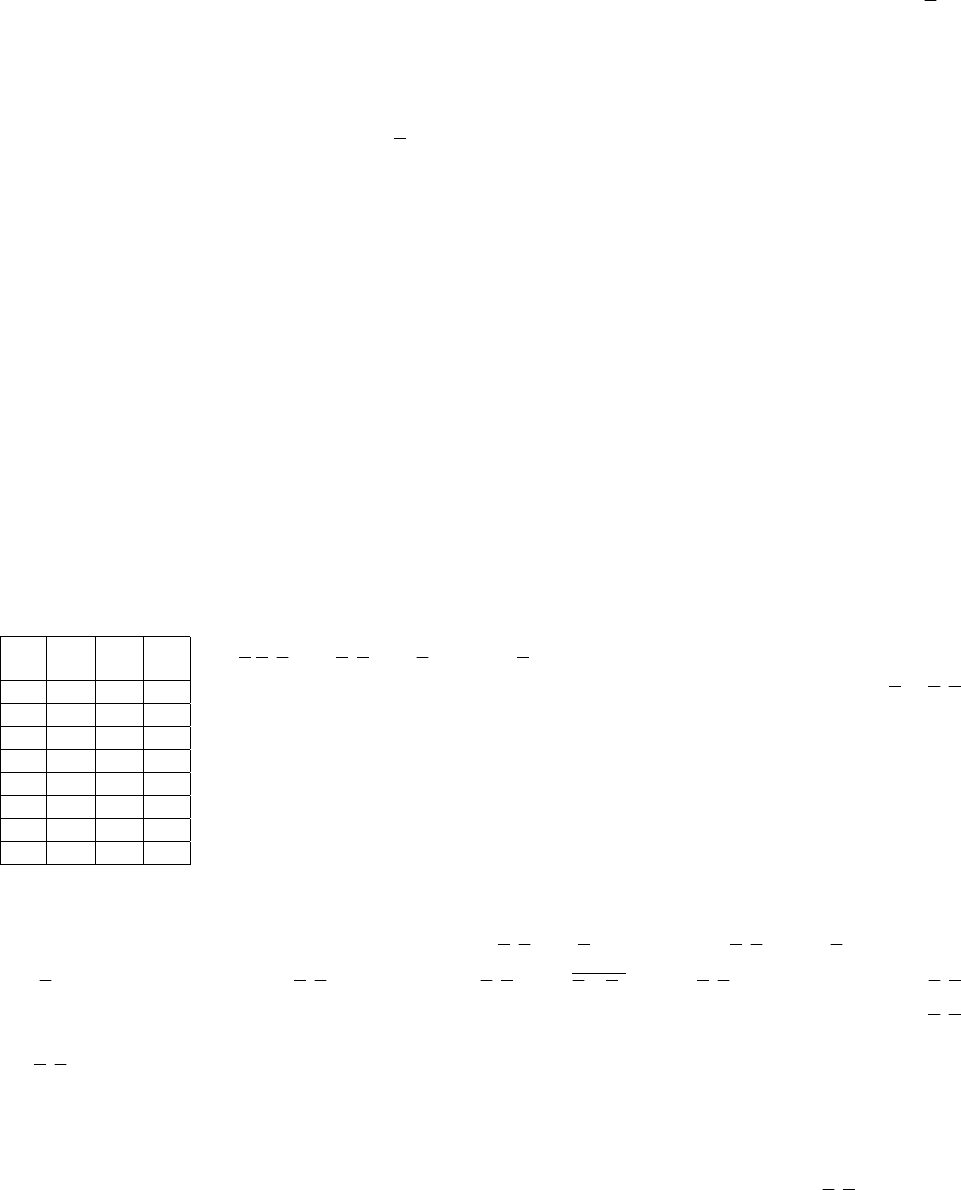
5) удаляются лишние константы в элементарных дизъюнкциях: ,
,
.
0
AA∨=
1 1
A
∨=
1 1
A
⋅=
Переход от КНФ к СКНФ осуществляется с использованием эквивалентности
()()
AAxAx
=∨⋅∨.
Рассмотрим последовательность действий для перехода от ДНФ к КНФ:
1) с помощью дистрибутивного закона переходят к конъюнкциям
элементарных дизъюнкций;
()(
xyz xy xz
∨=∨⋅∨
)
2) удаляются лишние дизъюнкции с помощью законов
,
и лишние
переменные в дизъюнкциях
,
AA A
⋅=
()
AAB A
⋅∨=
xxx∨=
1
xx∨=;
0
∨=
1 1
A
∨= 1
A
3) удаляются лишние константы в элементарных дизъюнкциях: ,
,
.
AA
1
⋅=
5. Минимизация логических функций
В данном разделе рассматривается проблема минимизации логических функций как задача
нахождения среди всех ДНФ, эквивалентных данной функции, той, которая содержит минимальное
вхождение букв.
5.1. Основные определения
Импликантой функции
называется такая элементарная конъюнкция над
множеством
{
, что
(
1
,,
n
fx x
…
)
}
K
1
,,
n
xx
…
()()
11
,, ,,
nn
Kfx x fx x
∨=…… .
Пример 1
1. Формула поглощения
, − импликанта.
xxyx
∨=
xy
2. Рассмотрим функцию трех переменных, заданную в виде таблицы.
СДНФ этой функции задается формулой
1
x
2
x
3
x
f
0 0 0 1
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
123 123 123 123 123
.
uxxxxxxxxxxxxxxx=∨∨∨∨
u
Любая элементарная конъюнкция в
формуле
является импликантой. Элементарные конъюнкции ,
1
xx
2 1
xx
2
,
2
xx
3
тоже являются импликантами.
Импликанта функции называется простой импликантой, если после
отбрасывания любой буквы из получается конъюнкция, не являющаяся
импликантой.
K f
K
13
xx
Например, для функции
, − простые импликанты;
− импликанта, но не простая.
(
12
xx
∨
)
3
x
12
xx
123
xx x
Пример 2
Упростим формулу
в примере 1, сделав слияние по переменной в первых двух конъюнкциях и
по
в двух последних. В результате получим
u
1
x
3
x
23 123
uxx xxx=∨
12
xx∨=
23 1 23 2
()
xx x xx x=∨⋅ ∨, так
как
23 2 2
xx x x x
∨=∨
3
, то
()
()
23 1 2 3 23 1 2 3 23
u xx x x x xx x x x xx
=∨ ∨=∨ ⋅ ∨
1
x
=
. Из формулы
12
xxx
∨
3
видно, что функция существенно зависит от переменных
, , . Поэтому в конъюнкции
f
1
x
2
x
3
x
23
xx
нельзя отбросить какую-либо переменную так, чтобы получилась снова импликанта. Таким образом,
,
1
x
23
xx
− простые импликанты.
Дизъюнкция всех простых импликант функции называется сокращенной ДНФ.
Справедлива следующая теорема.
Теорема 1
Любая логическая функция представима и при том однозначно в виде сокращенной ДНФ.
Для рассмотренной в примерах 1 и 2 функции сокращенной ДНФ является
12
xxx∨
3
, так как в
любой другой импликанте, соответствующей единичному набору, могут быть удалены переменные.
Дизъюнктивная нормальная форма называется минимальной, если она содержит наименьшее
число букв среди всех ДНФ, эквивалентных ей.
Дизъюнктивная нормальная форма называется тупиковой, если отбрасывание любой конъюнкции
или буквы приводит к ДНФ, которая не эквивалентна исходной ДНФ.
23

Определенные выше ДНФ − сокращенная, тупиковая и минимальная находятся в следующем
соотношении. Тупиковая ДНФ получается из сокращенной путем удаления некоторых слагаемых.
Минимальная ДНФ находится среди тупиковых.
5.2. Геометрическая интерпретация ДНФ
Множество всех наборов
можно рассматривать как множество вершин
n
-мерного куба.
Например, при
(
1
,,
n
αα…
)
i
)
i
1
)
}
3
n =
(
001
)
(
011
)
(
111
)
(
101
)
(
000
)
(
010
)
(
100
)
(
110
)
Рис.2.1. Геометрическая интерпретация
всех наборов функции трех переменных
Пусть
принимают фиксированные значения 0 или 1,
. Множество
вершин куба
таких, что , называется
(
-мерной гранью.
1
,,
r
i
σσ…
(
1
,,
α…
12 r
ii i n<<<≤…
)
nr
−
n
α
112 2
,,,
rr
iii i i
α=σα=σ α=σ…
Пример 3
1. Пусть в трехмерном кубе
,
,
. Тогда соответствующая грань будет образована
вершинами (100), (101), (110), (111). Ее размерность равна 2.
r
=
1
1
i
=
1
1
i
σ=
2.
,
, , , . Соответствующая грань размерности 1 образована
вершинами (001) и (101).
2
r
=
1
2
i =
2
3
i =
2
0
σ=
3
1
σ=
Пусть
− произвольная логическая функция. Обозначим
(
1
,,
n
fx x
…
()(
{
1
| ,
fn
α α…
)
1
,, , 1
n
Nf
=α α =…
−
)
множество единичных наборов. Если в качестве рассмотреть
элементарную конъюнкцию
f
()
12
12
1
,,
r
r
n
ii i
Kx x x x x
σσ σ
=⋅⋅⋅……,
то множество
называется интервалом r-го ранга. Легко видеть, что интервал
r
-го ранга
представляет собой
-мерную грань. Таким образом, интервал представляет собой множество
наборов, в которых компоненты, соответствующие переменным элементарной конъюнкции,
принимают фиксированные значения, а остальные компоненты равны 0 или 1. Интервалы
обозначаются наборами, в которых указываются фиксированные значения переменных, а остальные
компоненты помечаются знаком «−».
K
N
K
N
(
nr
−
Пример 4
Конъюнкциям
()
1123 2 3
,,
Kxxx x x
=⋅, соответствуют интервалы
()
2123
,,
Kxxx x
=
1
n
f
()()
{}
1
000 , 100
K
N
=
, .
()()
{}
2
100 , 101 ,(110),(111)
K
N
=
Этим интервалам соответствуют обозначения (− 00), (1 − −).
Если
, то:
()()()
111
,, ,, ,,
nn
fx x gx x hx x
=∨………
1)
, ;
gf
NN
⊆
hf
NN
⊆
2) .
fg
NNN
= ∪
24
